LRC （电感电阻电容）组成的二阶系统公式推导

首先从简化的 LC （电感电容）串联电路入手，分析阶跃信号下，电容两端电压的变化情况，对 LC （电感电容）电路进行公式推导，并进行了理论情况下的计算与仿真，因电池有内阻，导线和电感也都有电阻，所以实际情况下电阻不能忽略，因此 LC 实际测试结果与仿真结果有差异，从而引出了 LRC （电感电阻电容）电路的分析和推导，并进行了仿真验证。

LC （电感电容）电路中电容两端电压变化的函数推导

LC（电感电容）电路如下。

已知条件

从图中可知：

电源电压
$$v_s(t)=\{\begin{array}{l}0,t\le 0\\ V_I,t>0\end{array}$$

电容两端初始电压
$$v(0)=0$$

电感两端初始电流
$$i(0)=0$$

待求的电容两端电压函数为 v(t)

前置知识

• 电容伏安特性：$i=C\frac{dv}{dt}$
• 电感伏安特性：$v=L\frac{di}{dt}$
• 电感伏安特性的积分形式：
  $$\frac{1}{L}\begin{array}{r}\underset{-\infty }{\overset{t}{\int }}v\mathrm{d}t\end{array}=i$$

公式推导

根据节点法，流入节点电流等于流出节点的电流，有

$$\frac{1}{L}\begin{array}{r}\underset{-\infty }{\overset{t}{\int }}(V_I-v(t))\mathrm{d}t\end{array}=C\frac{dv(t)}{dt}$$

对方程两端进行对 t 求导

$$\frac{1}{L}(V_I-v(t))=C\frac{d^{2}v(t)}{d{t}^2}$$

移项整理得

$$LC\frac{d^{2}v(t)}{d{t}^2}+v(t)=V_I$$

这里 $L、C、V_I$ 都是已知常数，所以解上边这个二阶微分方程，就可以得到电容两端电压随时间变化的函数。

我们的目的是解出 $v(t)$

这里使用求特解加齐次解的方法解这个微分方程:

总的通解为特解+齐次解

$v(t)=v_p(t)+v_h(t)$

$v_p(t)$ ，特解

$v_h(t)$ ，齐次解

分为下面三个步骤：

1. 找出特解
2. 找出对应的齐次方程的通解
3. 根据初始条件计算通解中的常数参数

1.找特解

$$LC\frac{d^2{v}_p(t)}{d{t}^2}+v_p(t)=V_I$$

尝试 $v_p(t)=V_I$， 带入后满足方程，即
$$v_p(t)=V_I$$

2.找齐次方程通解

首先，令方程右边为 0，

$$LC\frac{d^{2}v(t)}{d{t}^2}+v(t)=V_I$$

得到对应的齐次方程：

$$LC\frac{d^2{v}_H(t)}{d{t}^2}+v_H(t)=0$$

设 $v_H(t)=A{e}^{st}$，找到满足齐次方程的 A 和 s，即可得到齐次解，
将 $v_H(t)=A{e}^{st}$带入上边的二阶微分方程：

$$LCA{s}^2{e}^{st}+A{e}^{st}=0$$

这里不需要 A = 0 的解，所以可以约掉 $A{e}^{st}$，化简为:

$$LC{s}^2+1=0$$

得到特征方程

$$s^2=-\frac{1}{LC}$$

开根号

$$s=\pm j\sqrt{\frac{1}{LC}}$$

记 ${\omega }_0=\sqrt{\frac{1}{LC}}$

上式可以简化成

$$s=\pm j{\omega }_0$$

根据二阶微分 $LC\frac{d^{2}v(t)}{d{t}^2}+v(t)=V_I$ ，可以看出 LC 的平方根的单位是时间，因此 ${\omega }_0=\sqrt{\frac{1}{LC}}$ 是频率（时间的倒数）

因此，可以得到齐次方程的通解：

$$v_H=A_1{e}^{j{\omega }_{0}t}+A_2{e}^{-j{\omega }_{0}t}$$

其中

$${\omega }_0=\sqrt{\frac{1}{LC}}$$

3.通过初始条件计算常数参数

现在得到了总的解

$$v=v_P+v_H$$

带入得

$$v=V_I+A_1{e}^{j{\omega }_{0}t}+A_2{e}^{-j{\omega }_{0}t}$$

其中

$${\omega }_0=\sqrt{\frac{1}{LC}}$$

根据已知的初始条件 $v_C(0)=0$，即 $v(0)=0$

带入可得

$$0=V_I+A_1+A_2$$

根据另一个已知条件 $i_L(0)=0$，因为：
$$i=C\frac{dv}{dt}$$

所以，当 t = 0 时，有

$$0=C{A}_{1}j{\omega }_0{e}^{j{\omega }_{0}t}+C{A}_2(-j{\omega }_0)e^{-j{\omega }_{0}t}$$

消掉公共项，可得

$$0=A_1-A_2$$

即
$$A_1=A_2$$

根据得到的方程组

$$\{\begin{array}{c}{A}_1=A_2\\ 0=V_I+A_1+A_2\end{array}$$

可以解得

$$A_1=A_2=-\frac{V_I}{2}$$

可以得到最终的 v(t) 的解为：

$$v(t)=V_I-\frac{V_I}{2}(e^{j{\omega }_{0}t}+e^{-j{\omega }_{0}t})$$

根据欧拉公式 $e^{jx}=cosx+jsinx$，上式还可整理成如下形式：

$$v(t)=V_I-V_{I}cos({\omega }_{0}t)$$

到此，推导结束，可以得到电容两端的电压以及电流($C\frac{dv}{dt}$)随时间的变化关系：

$$\begin{array}{c}v(t)=V_I-V_{I}cos({\omega }_{0}t)\\ i(t)=C{V}_I{\omega }_{0}sin({\omega }_{0}t)\end{array}$$

其中

$${\omega }_0=\sqrt{\frac{1}{LC}}$$

结果验证

取以下参数进行验证：

• 直流电压源电压 $V_I=1.3V$
• 电感 $L=3.7mH$
• 电容 $C=10uF$

1. 数学函数曲线

将选取的参数值带入电容电压函数中，得到
$$\begin{array}{c}v=1.3-1.3\ast \\ cos(\sqrt{\frac{1}{3.7\ast 10^{-3}\ast 10\ast 10^{-6}}}\ast t)\end{array}$$

绘制函数曲线如下

2. 仿真验证

根据选取的参数，在 LTspice 中进行仿真，与函数曲线结果一致，结果如下

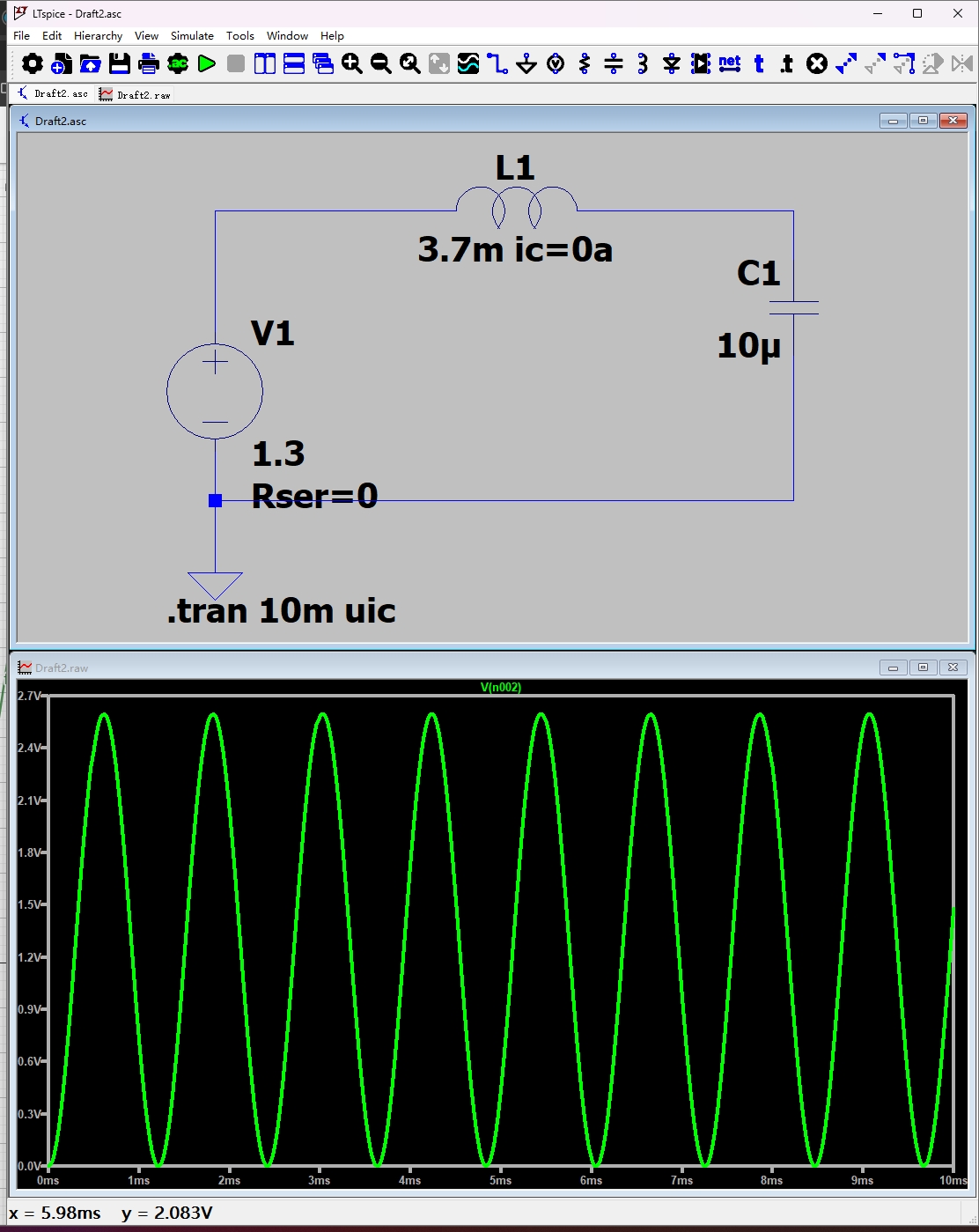
3. 实验验证

搭建了实验电路进行实际测试，发现结果与理论计算及仿真结果不一致，实验过程如下

1.实验电路

下图为实验用到的元件及装置，使用了 1.3V (标称1.2v，实测1.3v) 的 7 号电池 作为直流源，标称值 10uF 的电容，以及标称值 3.7mH 的电感线圈。

2.实验结果

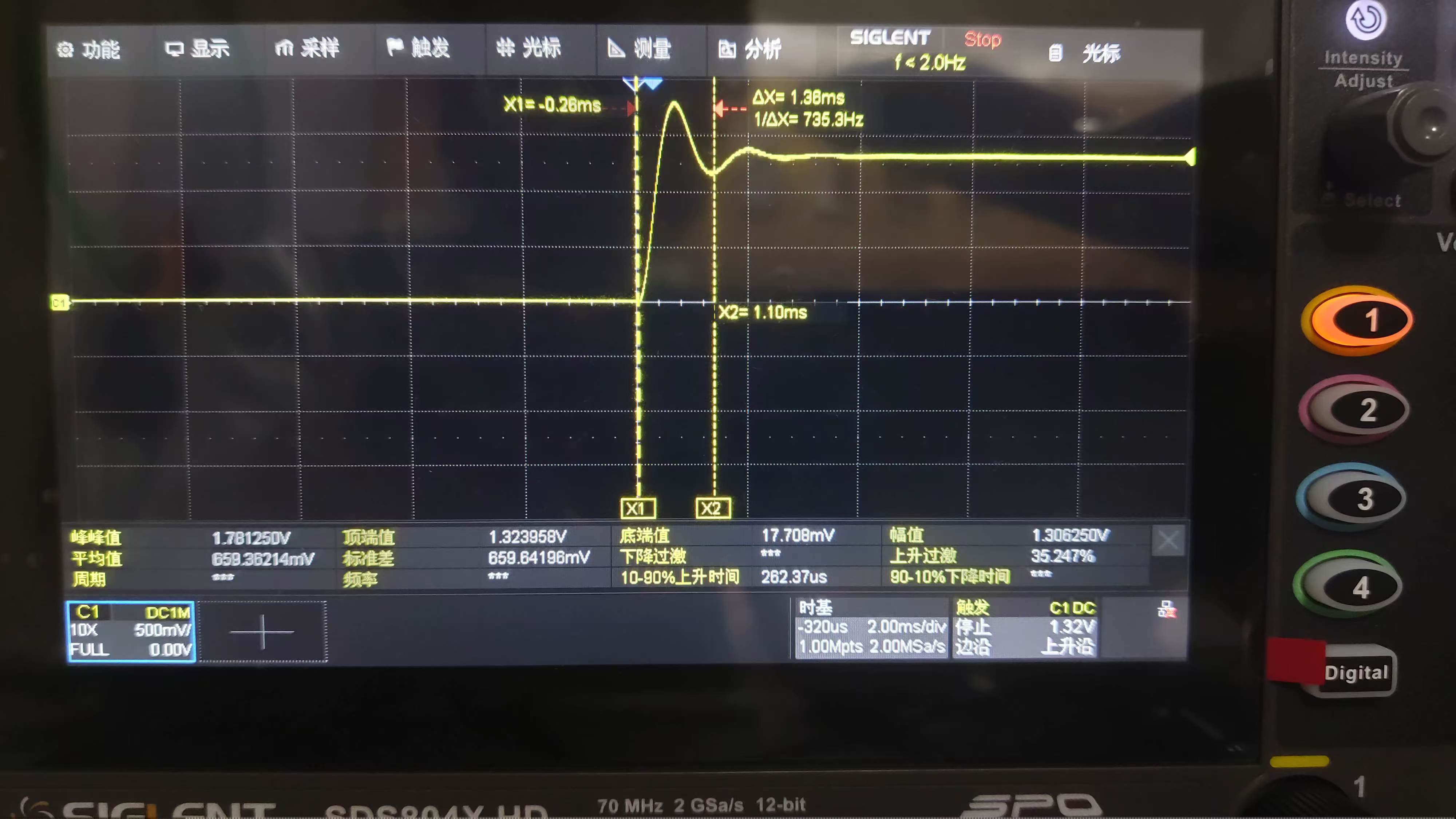
下图为示波器上升沿单次触发捕获的波形，可以看到波形与理论计算不一致。

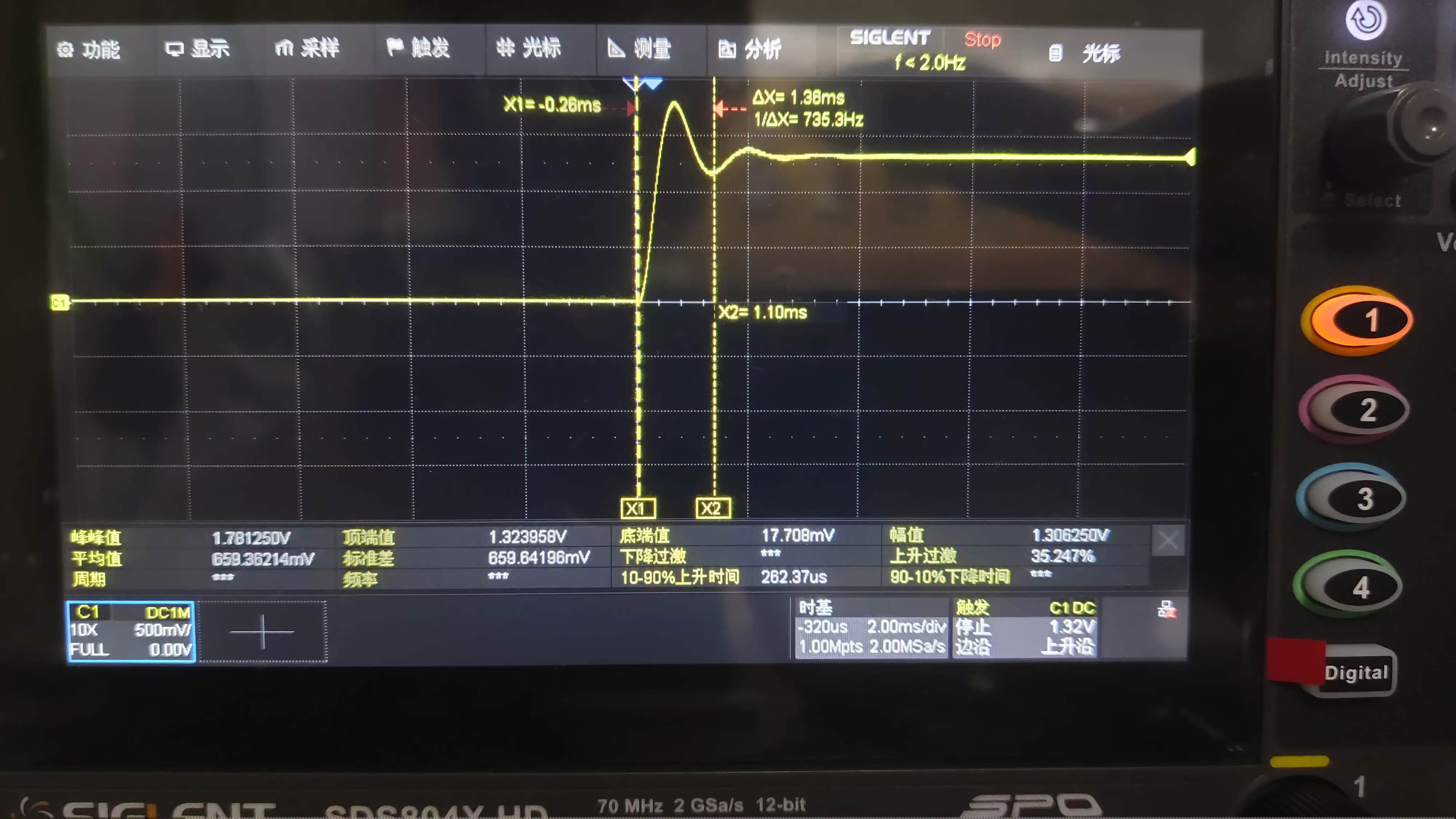
3.问题分析

这里不一致是因为电路中各部分包含的电阻所导致，电池包含内阻，导线、电感线圈都具有一定的电阻值，所以实际电路中还有电阻的串联需要考虑进去，下面继续对 LRC （电感电阻电容串联）电路进行分析。

LRC 电路公式推导

构造电路模型

根据上面的分析，我们实际实验的电路等效模型如下图所示

列 LRC 二阶微分方程

利用节点法，在图中红色的节点 v_A(t) 处，根据流入节点电流等于流出节点的电流，有：
$$\frac{1}{L}\underset{-\infty }{\overset{t}{\int }}(v_I(t)-v_A(t))\mathrm{d}t=\frac{v_A(t)-v(t)}{R}$$

根据电阻电容间的节点可以写出如下：

$$\frac{v_A(t)-v(t)}{R}=C\frac{dv(t)}{dt}$$

整理消元后得：

$$\begin{array}{c}\frac{1}{L}\underset{-\infty }{\overset{t}{\int }}(v_I(t)-C\frac{dv(t)}{dt}R-v(t))\mathrm{d}t\\ =C\frac{dv(t)}{dt}\end{array}$$

对两边对 t 进行微分：

$$LC\frac{d^{2}v(t)}{d{t}^2}=v_I(t)-C\frac{dv(t)}{dt}R-v(t)$$

移项并整理得：

$$\frac{d^{2}v(t)}{d{t}^2}+\frac{R}{L}\frac{dv(t)}{dt}+\frac{1}{LC}v(t)=\frac{v_I(t)}{LC}$$

这就是我们要解的 LRC 电路的二阶微分方程。

解 LRC二阶微分方程

设电压源输入信号为阶跃信号：
$$v_I(t)=\{\begin{array}{l}0,t\le 0\\ V_I,t>0\end{array}$$

初始条件为电容初始电压等于 0v， 电感初始电流等于 0A：

$v(0)=0,i(0)=0$

总的通解为特解+齐次解

$v(t)=v_p(t)+v_h(t)$

$v_p(t)$ ，特解

$v_h(t)$ ，齐次解

再次列出我们一直用的方法步骤：

1. 找出特解 v_p(t)
2. 找出对应的齐次方程的通解 v_h(t)
3. 根据初始条件计算通解中的常数参数

1. 找特解 v_p

$$\frac{d^2{v}_p(t)}{d{t}^2}+\frac{R}{L}\frac{d{v}_p(t)}{dt}+\frac{1}{LC}{v}_p(t)=\frac{V_I}{LC}$$

尝试 $v_p(t)=V_I$， 带入后等式成立，所以可以得到一个特解：
$$v_p=V_I$$

2. 找齐次解 v_h

$$\frac{d^2{v}_h(t)}{d{t}^2}+\frac{R}{L}\frac{d{v}_h(t)}{dt}+\frac{1}{LC}{v}_h(t)=0$$

尝试 $v_h(t)=A{e}^{st}$ 的形式，代入对应的齐次方程有：

$$A{s}^2{e}^{st}+\frac{R}{L}As{e}^{st}+\frac{1}{LC}A{e}^{st}=0$$

舍掉 A = 0 的情况，并约掉相同项，化简得到特征方程

$$s^2+\frac{R}{L}s+\frac{1}{LC}=0$$

引入新的符号简记方程，令

$$2\alpha =\frac{R}{L}$$

$${\omega }_0=\sqrt{\frac{1}{LC}}$$

特征方程对应的表示为

$$s^2+2\alpha s+{\omega }_0^2=0$$

解得：

$$\begin{array}{c}{s}_1=-\alpha +\sqrt{{\alpha }^2-{\omega }_0^2}\\ s_2=-\alpha -\sqrt{{\alpha }^2-{\omega }_0^2}\end{array}$$

可以的到齐次解为：

$$\begin{array}{c}{v}_h(t)=A_1{e}^{(-\alpha +\sqrt{{\alpha }^2-{\omega }_0^2})t}+\\ A_2{e}^{(-\alpha -\sqrt{{\alpha }^2-{\omega }_0^2})t}\end{array}$$

3. 根据初始条件计算未知常数

现在可以计算总的解为：

$$\begin{array}{c}v(t)=V_I+A_1{e}^{(-\alpha +\sqrt{{\alpha }^2-{\omega }_0^2})t}+\\ A_2{e}^{(-\alpha -\sqrt{{\alpha }^2-{\omega }_0^2})t}\end{array}$$

根据初始条件：

$$v(0)=0$$

可得
$$0=V_I+A_1+A_2$$

根据初始条件：

$$i(0)=0$$

以及电流方程：

$$\begin{array}{c}i(t)=C\frac{dv}{dt}\\ =C{A}_1(-\alpha +\sqrt{{\alpha }^2-{\omega }_0^2})e^{(-\alpha +\sqrt{{\alpha }^2-{\omega }_0^2})t}+\\ C{A}_2(-\alpha -\sqrt{{\alpha }^2-{\omega }_0^2})e^{(-\alpha -\sqrt{{\alpha }^2-{\omega }_0^2})t}\end{array}$$

可得：

$$\begin{array}{c}0=A_1(-\alpha +\sqrt{{\alpha }^2-{\omega }_0^2})+\\ A_2(-\alpha -\sqrt{{\alpha }^2-{\omega }_0^2})\end{array}$$

联立方程：

$$0=V_I+A_1+A_2$$
及
$$\begin{array}{c}0=A_1(-\alpha +\sqrt{{\alpha }^2-{\omega }_0^2})+\\ A_2(-\alpha -\sqrt{{\alpha }^2-{\omega }_0^2})\end{array}$$

可得最终的总解为：

$$\begin{array}{c}v(t)=V_I+A_1{e}^{(-\alpha +\sqrt{{\alpha }^2-{\omega }_0^2})t}+\\ A_2{e}^{(-\alpha -\sqrt{{\alpha }^2-{\omega }_0^2})t}\end{array}$$

其中，当 ${\alpha }^2-{\omega }_0^2\ne 0$ 时，

$$\begin{array}{c}{A}_1=\frac{V_I(\alpha +\sqrt{{\alpha }^2-{\omega }_0^2})}{-2\sqrt{{\alpha }^2-{\omega }_0^2}}\\ A_2=\frac{V_I(-\alpha +\sqrt{{\alpha }^2-{\omega }_0^2})}{-2\sqrt{{\alpha }^2-{\omega }_0^2}}\end{array}$$

当 ${\alpha }^2-{\omega }_0^2=0$ 时，对应后面临界阻尼的情况。

分情况讨论

根据 ${\alpha }^2-{\omega }_0^2$ 的正负关系，可以分三种情况讨论：

1. $\alpha >{\omega }_0$，为过阻尼 (Overdamped)

此时 $\sqrt{{\alpha }^2-{\omega }_0^2}$ 为实数，v(t) 可以简化为下面这个形式：

$$v(t)=V_I+A_1{e}^{-{\alpha }_{1}t}+A_2{e}^{-{\alpha }_{2}t}$$

可以绘制如下曲线，只看 t > 0 的部分，可以观察到过阻尼的响应曲线的形式。

2. $\alpha <{\omega }_0$，为欠阻尼 (Underdamped)

原式如下

$$\begin{array}{c}v(t)=V_I+A_1{e}^{(-\alpha +\sqrt{{\alpha }^2-{\omega }_0^2})t}+\\ A_2{e}^{(-\alpha -\sqrt{{\alpha }^2-{\omega }_0^2})t}\end{array}$$

因为 $ \alpha^2-\omega_02 < 0 $，所以在根号里可以提取出 -1， 原式可以化简为：

$$\begin{array}{c}v(t)=V_I+A_1{e}^{-\alpha t}{e}^{(j\sqrt{{\omega }_0^2-{\alpha }^2})t}+\\ A_2{e}^{-\alpha t}{e}^{(-j\sqrt{{\omega }_0^2-{\alpha }^2})t}\end{array}$$

为了简化方程，引入新的参数标记：

$${\omega }_d=\sqrt{{\omega }_0^2-{\alpha }^2}$$

则可简记为

$$v(t)=V_I+A_1{e}^{-\alpha t}{e}^{j{w}_{d}t}+A_2{e}^{-\alpha t}{e}^{-j{w}_{d}t}$$

根据欧拉公式：

$$e^{j{\omega }_{d}t}=cos({\omega }_{d}t)+jsin({\omega }_{d}t)$$

可以进一步化简

$$\begin{array}{c}v(t)=V_I+K_1{e}^{-\alpha t}cos({\omega }_{d}t)+\\ K_2{e}^{-\alpha t}sin({\omega }_{d}t)\end{array}$$

其中

$$K_1=A_1+A_2，K_2=(A_1-A_2)j$$

根据初始条件：$v(0)=0$，可以推出 $K_1=-V_I$

又因为：

$$\begin{array}{c}i(t)=C\frac{dv}{dt}\\ =-C{K}_1\alpha e^{-\alpha t}cos({\omega }_{d}t)-\\ C{K}_1{\omega }_d{e}^{-\alpha t}sin({\omega }_{d}t)-\\ C{K}_2\alpha e^{-\alpha t}sin({\omega }_{d}t)+\\ C{K}_2{\omega }_d{e}^{-\alpha t}cos({\omega }_{d}t)\end{array}$$

带入初始条件：$i(0)=0$，可得：

$$\begin{array}{c}0=-K_1\alpha +K_2{\omega }_d\\ K_2=-\frac{V_I\alpha }{{\omega }_d}\end{array}$$

将得到的 K₁, K₂ 带入可得

$$\begin{array}{c}v(t)=V_I-V_I{e}^{-\alpha t}cos({\omega }_{d}t)-\\ V_I\frac{\alpha }{{\omega }_d}{e}^{-\alpha t}sin({\omega }_{d}t)\end{array}$$

根据以下公式可知，同频率不同幅度的正余弦函数相加，可以写成一个正弦或者余弦的形式，如下：
$$\begin{array}{c}{A}_{1}cos(\theta )+A_{2}sin(\theta )\\ =\sqrt{A_1^2+A_2^2}cos(\theta -ta{n}^{-1}(\frac{A_2}{A_1}))\\ =\sqrt{A_1^2+A_2^2}sin(\theta +ta{n}^{-1}(\frac{A_1}{A_2}))\end{array}$$

$$\begin{array}{c}{A}_{1}cos(\theta )-A_{2}sin(\theta )\\ =\sqrt{A_1^2+A_2^2}cos(\theta +ta{n}^{-1}(\frac{A_2}{A_1}))\\ =\sqrt{A_1^2+A_2^2}sin(\theta -ta{n}^{-1}(\frac{A_1}{A_2}))\end{array}$$

可以把 v(t) 化简为一个余弦的形式

$$\begin{array}{c}v(t)=V_I-\\ V_I\frac{{\omega }_0}{{\omega }_d}{e}^{-\alpha t}cos({\omega }_{d}t-ta{n}^{-1}\frac{\alpha }{{\omega }_d})\end{array}$$

最终得到欠阻尼条件下 LRC 电路电容两端电压的表达式为：

$$\begin{array}{c}v(t)=V_I-\\ V_I\frac{{\omega }_0}{{\omega }_d}{e}^{-\alpha t}cos({\omega }_{d}t-ta{n}^{-1}\frac{\alpha }{{\omega }_d})\end{array}$$

其中，

$$\alpha =\frac{R}{2L}$$

$${\omega }_0=\sqrt{\frac{1}{LC}}$$

$${\omega }_d=\sqrt{{\omega }_0^2-{\alpha }^2}$$

可以绘制如下曲线，只看 t > 0 的部分，可以观察到欠阻尼的响应曲线的形式。

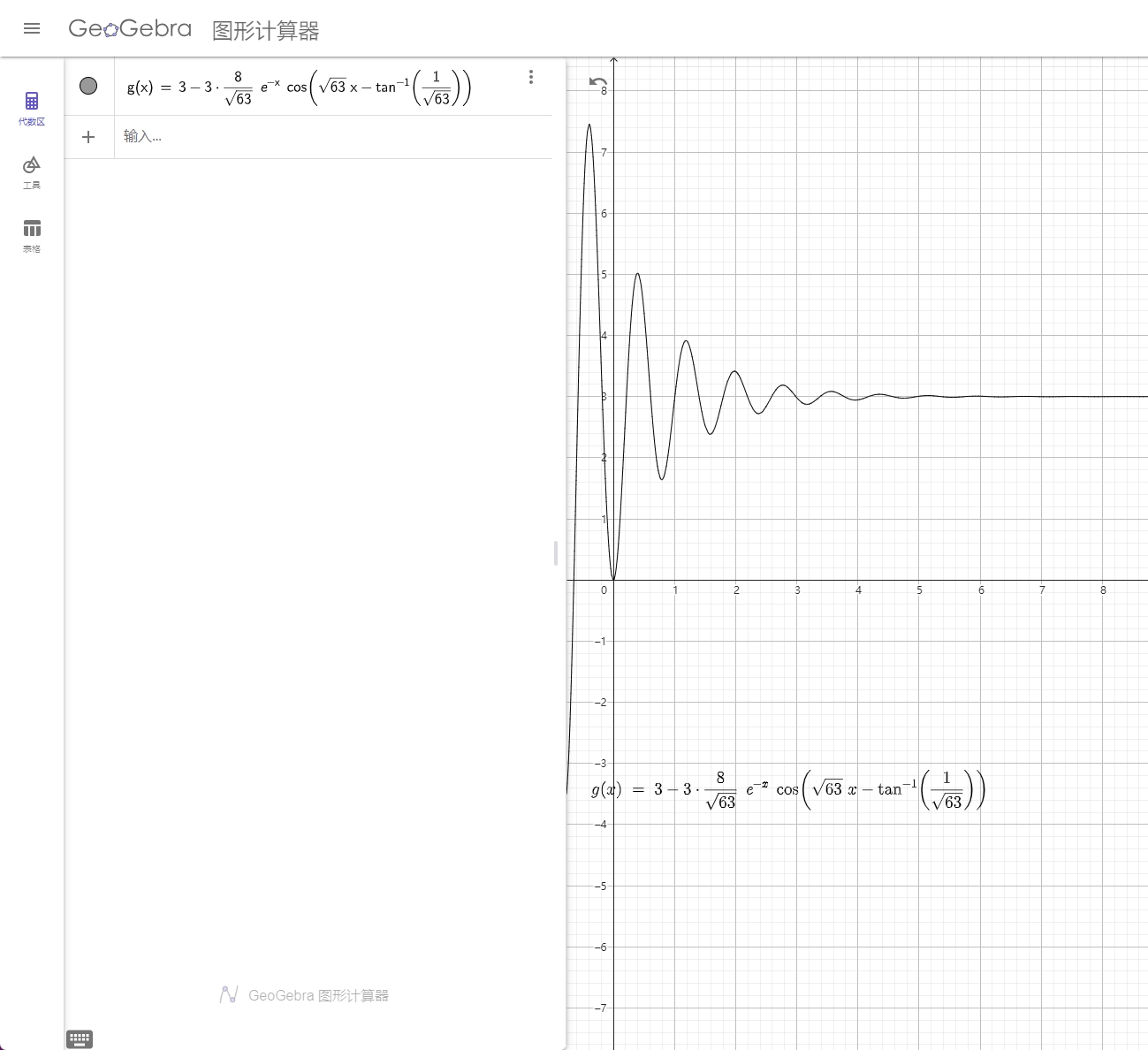
3. $\alpha ={\omega }_0$，为临界阻尼 (Critically damped)

这种情况暂时还没搞明白，后边搞明白了再补充。

快速判断输出波形的方法

通过下面的方法，可以快速判断电容两端的波形

首先计算两个参数

$$波形的频率{\omega }_d=\sqrt{{\omega }_0^2-{\alpha }^2}$$

$$品质因数Q=\frac{{\omega }_0}{2\alpha }$$

利用 $T=\frac{2\pi }{{\omega }_d}$ 可以计算最终震荡的周期，品质因数 Q 表示震荡的周期个数，即震荡 Q 个波形后趋于电压VI。

LRC 理论验证

回忆一下实验中设定的参数：

• 直流电压源电压 $V_I=1.3V$
• 电感 $L=3.7mH$
• 电容 $C=10uF$

并且通过调整仿真结果，与实际结果波形对比，可以推测 电阻 $R=18\Omega$。

快速推断大概波形

带入上边的公式计算频率和品质因数如下：

$${\omega }_d=\sqrt{\frac{1}{LC}-(\frac{R}{2L}{)}^2}$$

带入已知参数

$$\begin{gathered} \begin{array}{c}{\omega }_d=\\ \sqrt{\frac{1}{3.7\ast 10^{-3}\ast 10\ast 10^{-6}} \\ -(\frac{18}{2\ast 3.7\ast 10^{-3}}{)}^2}\end{array} \end{gathered}$$

解得

$${\omega }_d=4594.594$$

可以进一步得到周期

$$T=\frac{2\pi }{{\omega }_d}=0.0013675s=1.3675ms$$

继续计算品质因数

$$\begin{array}{l}Q=\frac{{\omega }_0}{2\alpha }\\ =\frac{\sqrt{\frac{1}{LC}}}{\frac{R}{L}}\\ =\frac{\sqrt{\frac{1}{3.7\ast 10^{-3}\ast 10\ast 10^{-6}}}}{\frac{18}{3.7\ast 10^{-3}}}\\ =1.06863244\end{array}$$

根据结果可以推断出，波形在震荡一个波形后收敛于输入电压 1.3v，并且波形的周期为 1.3675 毫秒。

精确计算

$$\begin{array}{c}\alpha =\frac{R}{2L}=\frac{18}{2\ast 3.7\ast 10^{-3}}=2432.432\\ {\omega }_0=\sqrt{\frac{1}{LC}}\\ =\sqrt{\frac{1}{3.7\ast 10^{-3}\ast 10\ast 10^{-6}}}=5198.75245\end{array}$$
$${\omega }_d=\sqrt{{\omega }_0^2-{\alpha }^2}=4594.594$$
$\alpha <{\omega }_0$，为欠阻尼，带入公式

$$\begin{array}{c}v(t)=V_I-\\ V_I\frac{{\omega }_0}{{\omega }_d}{e}^{-\alpha t}cos({\omega }_{d}t-ta{n}^{-1}\frac{\alpha }{{\omega }_d})\end{array}$$

带入绘图可得

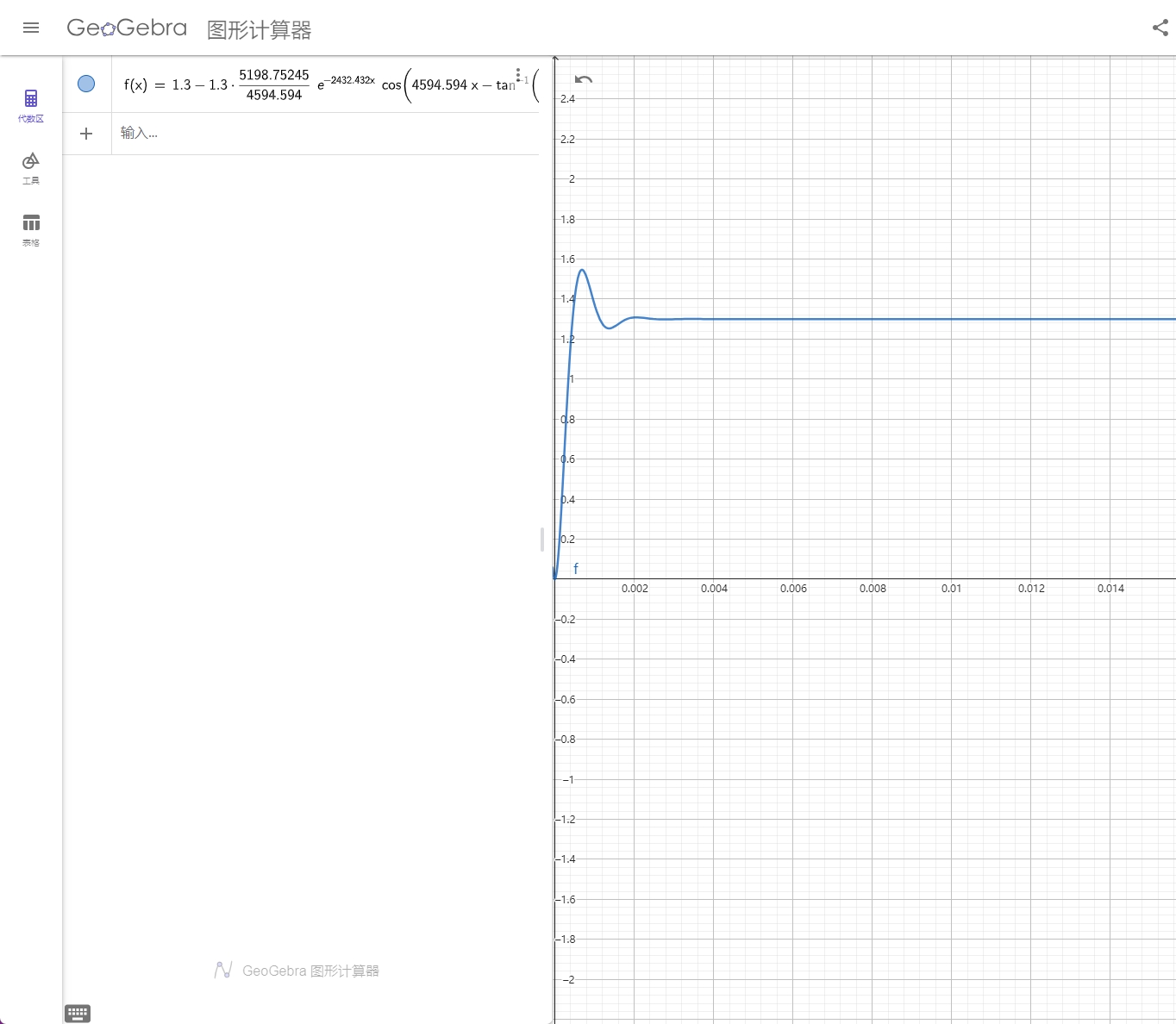
LRC 电路仿真验证

通过修改仿真电路，增加电阻 R ，调整 R 的值，使仿真波形与实验结果一致，大概可以看出整个电路中的引入电阻大概为 18 欧，仿真结果与实际结果均与计算结果一致，震荡一个周期后收敛与 1.3v，周期为 1.3ms 左右。

参考

麻省理工学院公开课——电路与电子学 p16.二阶系统上

https://www.bilibili.com/video/BV1ts411v7Ep?p=16

麻省理工学院公开课——电路与电子学 p17.二阶系统下

https://www.bilibili.com/video/BV1ts411v7Ep?p=17