梯度下降法多变量求线性回归
实际情况下很多时候所需求的目标不止一个因素影响会有多个,因此更多情况下多个变量会更加贴近生活现实
下面以俩个因素变量为例:
初始化:

lr = 0.0002 num = 100000 w = np.array([[0.5214, 0.5215]])
定义模型(也是预测值):
yy = np.matmul(w, x.T)#
x.T对张量x进行转置--11*2变为2*11
之后进行迭代
loss = 1 / 2.0 * np.sum((np.matmul(w, x.T) - y) ** 2)
w_list = []
loss_list = []
loss_list.append(loss)
for i in range(num):
w_gra = np.mean(np.matmul((yy - y), x))
w = w - lr * w_gra
loss = 1 / 2.0 * np.sum((np.matmul(w, x.T) - y) ** 2)
if loss > loss_list[-1]:
break
w_list.append(w)
loss_list.append(loss)
print(f"迭代第{i}次,梯度为{w_gra:10f},权重为:{w},损失:{loss:10f}")
之后进行预测值和真实值的对比

证明误差几乎可以忽略不记,对于这个数据来说w的值接近为1
完整代码:
import numpy as np
import torch
x = np.array([[0.180, 0.001 * 1], [0.100, 0.001 * 2],
[0.160, 0.001 * 3], [0.080, 0.001 * 4],
[0.090, 0.001 * 5], [0.110, 0.001 * 6],
[0.120, 0.001 * 7], [0.170, 0.001 * 8],
[0.150, 0.001 * 9], [0.140, 0.001 * 10],
[0.130, 0.001 * 11]
]) # 11*2
y = np.array([[0.180 + 0.001 * 1, 0.100 + 0.001 * 2,
0.160 + 0.001 * 3, 0.080 + 0.001 * 4,
0.090 + 0.001 * 5, 0.110 + 0.001 * 6,
0.120 + 0.001 * 7, 0.170 + 0.001 * 8,
0.150 + 0.001 * 9, 0.140 + 0.001 * 10,
0.130 + 0.001 * 11]
]) # 真实值
# 初始化
lr = 0.0002
num = 100000
w = np.array([[0.5214, 0.5215]])
# 定义模型
yy = np.matmul(w, x.T) # x.T对张量x进行转置--11*2变为2*11
# 定义目标函数:
loss = 1 / 2.0 * np.sum((np.matmul(w, x.T) - y) ** 2)
w_list = []
loss_list = []
loss_list.append(loss)
for i in range(num):
w_gra = np.mean(np.matmul((yy - y), x))
w = w - lr * w_gra
loss = 1 / 2.0 * np.sum((np.matmul(w, x.T) - y) ** 2)
if loss > loss_list[-1]:
break
w_list.append(w)
loss_list.append(loss)
print(f"迭代第{i}次,梯度为{w_gra:10f},权重为:{w},损失:{loss:10f}")
print(w)
yy = np.matmul(w, x.T)
print("预测值:", yy)
print("真实值:", y)
结果:
 梯度下降法进行多变量进行二分类
梯度下降法进行多变量进行二分类

数据的准备和初始化


以y=150为界限,把个体分为两类
迭代:
for i in range(num):
mis_flag = False
for i in range(n_samples):
y_fre = np.dot(weights, x[i])+bias
#判断是不是wu'fen
if y_fre * y[i] <= 0 :
weights +=lr * y[i] * x[i]
bias +=lr *y[i]
mis_flag =True
if not mis_flag:
break
print(weights)
print(bias)迭代完之后,确定了w和bias的值
对每个样本的y值进行区分
y的计算公式为:
pre = np.dot(weights , x[i])+bias
具体代码为:
y_fre = []
for i in range(n_samples):
pre = np.dot(weights , x[i])+bias
if(pre >= 0):
y_fre.append(1)
else:
y_fre.append(-1)
print(y)
print(y_fre)完整代码:
import numpy as np
import matplotlib.pyplot as plt
#数据
x = np.array([[0.180, 0.001 * 1], [0.100, 0.001 * 2],
[0.160, 0.001 * 3], [0.080, 0.001 * 4],
[0.090, 0.001 * 5], [0.110, 0.001 * 6],
[0.120, 0.001 * 7], [0.170, 0.001 * 8],
[0.150, 0.001 * 9], [0.140, 0.001 * 10],
[0.130, 0.001 * 11]
]) # 11*2
#分类标签
y = np.array([+1,-1,+1,-1,-1,-1,-1,+1,+1,+1,-1])
n_samples , n_features = x.shape
#初始化
weights = np.zeros(n_features)
bias = 0.0
lr = 0.0001
num = 100000
for i in range(num):
mis_flag = False
for i in range(n_samples):
y_fre = np.dot(weights, x[i])+bias
#判断是不是wu'fen
if y_fre * y[i] <= 0 :
weights +=lr * y[i] * x[i]
bias +=lr *y[i]
mis_flag =True
if not mis_flag:
break
print(weights)
print(bias)
y_fre = []
for i in range(n_samples):
pre = np.dot(weights , x[i])+bias
if(pre >= 0):
y_fre.append(1)
else:
y_fre.append(-1)
print(y)
print(y_fre)
运行结果:

y已经被区分好了
感知机的概念:

 模型:
模型:

作用:
分类:loss = (y_pre-y)^2还需要分段函数
回归:loss = (y_pre-y)^2(梯度下降法)
两个都需要求导:loss对权重(w)求导,
loss对偏置(bias)求导
激活函数
1,什么是激活(映射)函数作用是什么?:
激活函数(Activation Function)是一种添加到人工神经网络中的函数,旨在帮助网络学习数据中的复杂模式。类似于人类大脑中基于神经元的模型,激活函数最终决定了要发射给下一个神经元的内容。
作用:不使用激活函数的话,神经网络的每层都只是做线性变换,多层输入叠加后也还是线性变换。因为线性模型的表达能力通常不够,所以这时候就体现了激活函数的作用了,激活函数可以引入非线性因素。
2,常用激活函数:
(1)Sigmoid函数:
公式:

导数:
![]()
图像(左:原函数,右:导数):
 特点:它能够把输入的连续实值变换为0和1之间的输出,特别的,如果是非常大的负数,那么输出就是0;如果是非常大的正数,输出就是1.因为这个特点sigmoid函数特别适用于将预测概率作为输出的模型
特点:它能够把输入的连续实值变换为0和1之间的输出,特别的,如果是非常大的负数,那么输出就是0;如果是非常大的正数,输出就是1.因为这个特点sigmoid函数特别适用于将预测概率作为输出的模型
优点:便于求导的平滑函数,函数是可微的
缺点: 容易出现gradient vanishing--梯度消失,函数输出并不是zero-centered(中心化),幂运算相对来讲比较耗时
(2)ReLu函数
公式:

图像:

优点:在x>0的情况下不会出现梯度饱和,梯度消失的问题,收敛速度快,运算速度也快
缺点:输出值都是非0,存在神经元死亡在x<0时,梯度为零。这个时候神经元及之后的神经元永远梯度为0 ,不再对任何数据有影响,导致参数不再更新
(3)Tanh函数
公式:

图像:

它和sigmoid很像,但是还是有区别的:

优点 :输出均值是0,收敛速度要比sigmo快,可减少迭代次数
缺点:需要幂运算,计算成本高,也存在梯度消失
(4)Softmax函数
公式 :

图像:

Softmax 是用于多类分类问题的激活函数,在多类分类问题中,超过两个类标签则需要类成员关系。对于长度为 K 的任意实向量,Softmax 可以将其压缩为长度为 K,值在(0,1)范 围内,并且向量中元素的总和为 1 的实向量。只能用在输出层神经上 。
主要缺点:
在0 时不可微。负输入的梯度为零,这意味着对于该区域的激活,权重不会在反向传播期间更新,因此会产生永不激活的死亡神经元。
多层感知机:
多层感知机分为输入层,隐藏层,输出层。除了输入层没有激活函数,其他都有。
多层感知机思路就是将一次不能完成学习的东西分多次进行学习。针对XOR问题就是先学一个x,再学一个y,然后再将这两次学习的结果组合起来。
最后的出来的y是嵌套复合函数
隐藏层可以有多个:

BP神经网络:
bp神经网络全称为Back Propagation Neural Network,简称为BPNN
BP神经网络的原理就像下面的图一样,模仿人的大脑的原理,把看到的东西作为输入,然后经过大脑,最后作为输出。
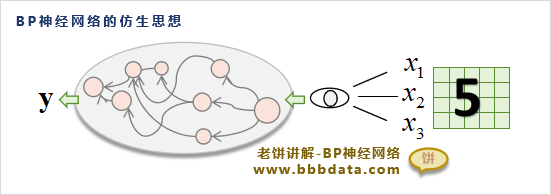
他的数学公式:

这是一个只有一个隐层的BP神经网络(加上输入层、输出层,称为三层BP神经网络),
BP神经网络也可以有多个隐层,多层的BP神经网络结构图如下:

多个隐层的BP神经网络的数学表达式进行套娃就可以了,
学习时先用三层的进行理解,因为三层的使用得较多。
BP使用均方差函数来评估网络的误差,它的公式如下:
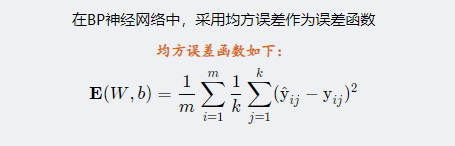





















 394
394

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








