机器学习实践 CH13 利用PCA来简化数据
一.引例
通过电视观看足球赛事时显示器大概包含100多万像素,同时人主要关注的是显示器中的球的位置,而球只需要很少的像素组成,此时人们就可以将显示器中的上百万个像素转换成一个三维图像,该图像就给出了球在运动场上的位置。上述图像从一百万维降到三维的过程就被称作降维。本章主要介绍降维技术中的主成分分析法(PCA)。
二.降维技术的使用原因
1.使得数据集更易使用;
2.降低很多算法的计算开销;
3.去除噪声;
4.使得结果易懂;
三.PCA简介
在PCA中数据从原来的坐标系转换到了新的坐标系,新坐标系的选择是由数据本身决定的。第一个新坐标轴选择的是原始数据中方差最大的方向,第二个新坐标轴的选择和第一个坐标轴正交且有最大的方差方向。该过程一直重复,重复次数为原始数据中特征的数目。我们会发现大部分方差都包含在最前面的几个新坐标轴中。因此我们可以忽略余下的坐标轴,即对数据进行降维处理。
四.PCA代码
from numpy import * #引入numpy模块
def loadDataSet(fileName, delim=’\t’):
fr = open(fileName) #打开文件
stringArr = [line.strip().split(delim) for line in fr.readlines()] # 读取整个文件,并制成行的列表,去掉列表前后空,并以‘\t’为间隔分开
datArr = [map(float,line) for line in stringArr] #把数据 float 化
return mat(datArr) 函数返回值
def pca(dataMat, topNfeat=9999999):
meanVals = mean(dataMat, axis=0) #求矩阵每一列的均值
meanRemoved = dataMat - meanVals #每一列减去相应的均值
covMat = cov(meanRemoved, rowvar=0) #求去掉均值后的矩阵的协方差矩阵
eigVals,eigVects = linalg.eig(mat(covMat))#求矩阵的特征值,特征向量
eigValInd = argsort(eigVals) #对特征值从小到大进行排序,获得排序前的序号
eigValInd = eigValInd[:-(topNfeat+1):-1] #从后往前取topNfeat个数
redEigVects = eigVects[:,eigValInd] #取出其对应的特征向量
lowDDataMat = meanRemoved * redEigVects#转换数据到新的空间
reconMat = (lowDDataMat * redEigVects.T) + meanVals
return lowDDataMat, reconMat
def replaceNanWithMean(): # 将所有的NAN替换成平均值
datMat = loadDataSet(‘secom.data’, ’ ‘)
numFeat = shape(datMat)[1]
for i in range(numFeat):
meanVal = mean(datMat[nonzero(~isnan(datMat[:,i].A))[0],i]) #values that are not NaN (a number)
datMat[nonzero(isnan(datMat[:,i].A))[0],i] = meanVal #set NaN values to mean
return datMat
图1.代码:
from numpy import *
import matplotlib
import matplotlib.pyplot as plt
import pca
dataMat = pca.loadDataSet(‘testSet.txt’)
lowDMat, reconMat = pca.pca(dataMat, 1)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(dataMat[:,0], dataMat[:,1], marker=’^’, s=90)
ax.scatter(reconMat[:,0], reconMat[:,1], marker=’o’, s=50, c=’red’)
plt.show()
图2.代码:
from numpy import *
import matplotlib
import matplotlib.pyplot as plt
import pca
dataMat = pca.replaceNanWithMean()
below is a quick hack copied from pca.pca()
meanVals = mean(dataMat, axis=0)
meanRemoved = dataMat - meanVals #remove mean
covMat = cov(meanRemoved, rowvar=0)
eigVals,eigVects = linalg.eig(mat(covMat))
eigValInd = argsort(eigVals) #sort, sort goes smallest to largest
eigValInd = eigValInd[::-1]#reverse
sortedEigVals = eigVals[eigValInd]
total = sum(sortedEigVals)
varPercentage = sortedEigVals/total*100
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(range(1, 21), varPercentage[:20], marker=’^’)
plt.xlabel(‘Principal Component Number’)
plt.ylabel(‘Percentage of Variance’)
plt.show()
图1.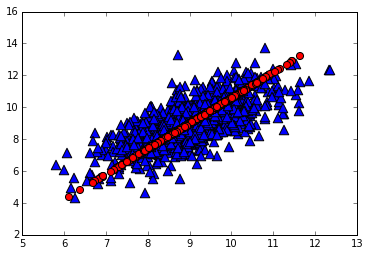
图2.








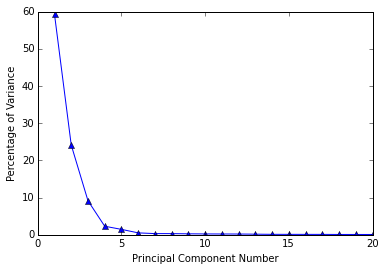














 664
664

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








