在使用计算机求根的时候,由于计算机的数字离散性,通常需要通过试一试的方法确定一个初始值,然后根据这个初始值重复迭代过程,使其最后的函数值趋近于0。但是更多的时候,我们需要让这个过程在计算机中自动进行。目前使用普遍的初始值的猜想方法主要有两个:
1、交叉法(Bracketing Methods):基于两个猜想的初始值坐落在两边,假想根在这两个初始值的中间;
2、开型法(Open Methods):可以涉及到一个或多个初始值的猜想,但是没必要将初始值放在实际的根的两边;
比较两种方法,Bracketing Methods几乎在所有情况下都能使用,但是收敛速度较慢,需要更多的迭代次数;而Open Methods在有些情况下不能使用,但是收敛速度较快。
下面首先介绍几种Bracketing Methods:
1、增量搜索(Intcremental Search)
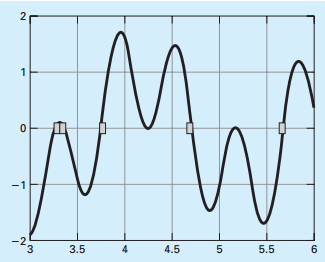
假如两个上下初始值有式子 f(xl)f(xu) < 0,xl表示较小的初始值猜想,xu表示较大的初始值猜想。则至少有一个实根在xl和xu之间。增量搜索有一个搜索精度问题:通常情况下,值得确定出现在f(xl)f(xu)的值改变方向的时候,但是如果每次搜索的步长太小,就会导致迭代次数过多,收敛时间很长;如果搜索步长较大就可能导致空间上最接近,最精确的那个跟被丢掉。如下图:
上图中最右边的根有可能因为搜索步长太大而被丢失。
下面是Matlab的Incremental Search函数:
function xb = incsearch(func,xmin,xmax,ns)
% incsearch: incremental search root locator
% xb = incsearch(func,xmin,xmax,ns):
% finds brackets of x that contain sign changes
% of a function on an interval
% input:
% func = name of function
% xmin, xmax = endpoints of interval
% ns = number of subintervals (default = 50)
% output:
% xb(k,1) is the lower bound of the kth sign change
% xb(k,2) is the upper bound of the kth sign change
% If no brackets found, xb = [].
if nargin < 3
error('At least 3 arguments required');
end
if nargin < 4
ns = 50;
end
x = linspace(xmin,xmax,ns);
f = func(x);
nb = 0;
xb = [];
for k = 1 : length(x) - 1
if sign(f(k)) ~= sign(f(k + 1))
nb = nb + 1;
xb(nb,1) = x(k);
xb(nb,2) = x(k + 1);
end
end
if isempty(xb)
disp('No brackets found')
disp('Check interval or increase ns')
else
disp('Number of brackets: ')
disp(nb)
endf(x) = sin(10x) + cos(3x)
5
ans =
3.2449 3.3061
3.3061 3.3673
3.7347 3.7959
4.6531 4.7143
5.6327 5.6939
这是根的位置图:
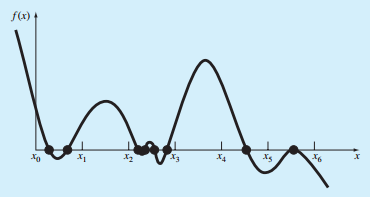
对分法如下图所示:首先猜想出两个初始值,找到两个初始值的中间位置,两个初始值分别与中间位置坐标的函数值乘积,如果函数值乘积小于0,则选择函数值乘积小于0的那一边进行迭代,以下的步奏以此类推。
function [root, fx, ea, iter] = bisect(func,xl,xu,es,maxit,varargin)
% bisect: root location zeroes
% [root,fx,ea,iter]=bisect(func,xl,xu,es,maxit,p1,p2,...):
% uses bisection method to find the root of func
% input:
% func = name of function
% xl, xu = lower and upper guesses
% es = desired relative error (default = 0.0001%)
% maxit = maximum allowable iterations (default = 50)
% p1,p2,... = additional parameters used by func
% output:
% root = real root
% fx = function value at root
% ea = approximate relative error (%)
% iter = number of iterations
if nargin < 3
error('At least 3 input arguments required');
end
test = func(xl,varargin{:}) * func(xu,varargin{:});
if test > 0
error('No sign change');
end
if nargin < 4 | isempty(es)
es = 0.0001;
end
if nargin < 5 | isempty(maxit)
maxit = 50;
end
iter = 0;
xr = xl;
ea = 100;
while(1)
xrold = xr;
xr = (xl + xu)/2;
iter = iter + 1;
if xr ~= 0
ea = abs((xr - xrold)/xr) * 100;
end
test = func(xl,varargin{:}) * func(xr,varargin{:});
if test < 0
xu = xr;
elseif test > 0
xl = xr;
else
ea = 0;
end
if ea <= es | iter >= maxit
break;
end
end
root = xr;
fx = func(xr,varargin{:});
这里同时定义了相对误差:
x_new是当前迭代值,x_old是前一次的迭代值。迭代的时候需要满足一定的的误差条件,只要满足一定的误差范围,可以中断迭代,得到最终的值。
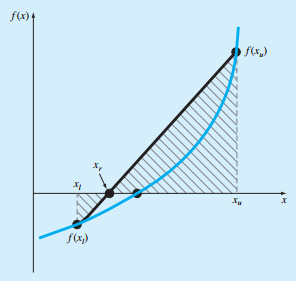
3、试位法(False Position Method),也可以叫线性插值法(Linear Interpolation Method)
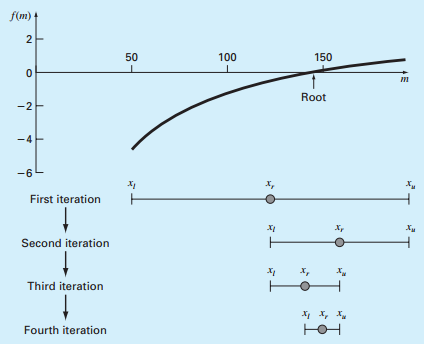
通过函数值上面的两个点画出直线,与x轴的交点找到xr。根据xr得到一个函数值,并且用xr替换与xl和xu中函数值符号相同的端值。以此进行迭代。xr的计算方程如下:








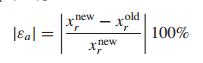
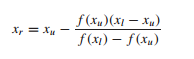














 746
746

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








