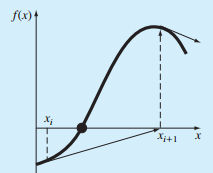
求根的方法有很多,前面介绍了用交叉法(Bracketing Method)求函数的根,本文介绍几种用开型法(Open Methods)求根的方法。但着重介绍牛顿-拉普森(Newton-Raphson)法。在Bracketing Methods中,一般需要两个初始的猜想值,用于迭代的起始。但是在Open Methods中,只需要一个起始值或者两个但是不需要让它们分布在精确值对的两侧。但是Open Methods方法的缺点是,在有些情况下他不能得到收敛的值,如下图:
1、牛顿-拉普森(Newton-Raphson)方法
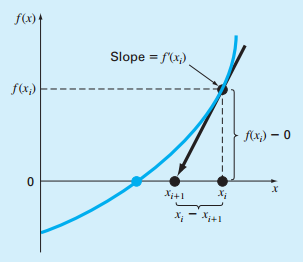
牛顿-拉普森迭代算法的推导,如图:
斜率slope能通过如下方程得到:
其中,xi为开始的假设值。则下一个x值的求取形式如下:








 本文介绍了数值分析中开型法(Open Methods)求根,重点讲解了牛顿-拉普森(Newton-Raphson)方法的迭代公式,通过实例展示了即使初始预测不佳,最终仍能收敛到正确结果。同时提到了Secant Method、Modified Secant Method和Brent's Method,这些方法在处理多根和特定情况时可能更具挑战性。
本文介绍了数值分析中开型法(Open Methods)求根,重点讲解了牛顿-拉普森(Newton-Raphson)方法的迭代公式,通过实例展示了即使初始预测不佳,最终仍能收敛到正确结果。同时提到了Secant Method、Modified Secant Method和Brent's Method,这些方法在处理多根和特定情况时可能更具挑战性。
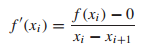
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 767
767

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








