数学建模—投资组合问题

引言

 求解问题来之98年的数模赛题（一道比笔者还老的经典老题），在阅读了几篇相关文献的同时，结合建模课给出的ppt汇总成此文。

上题

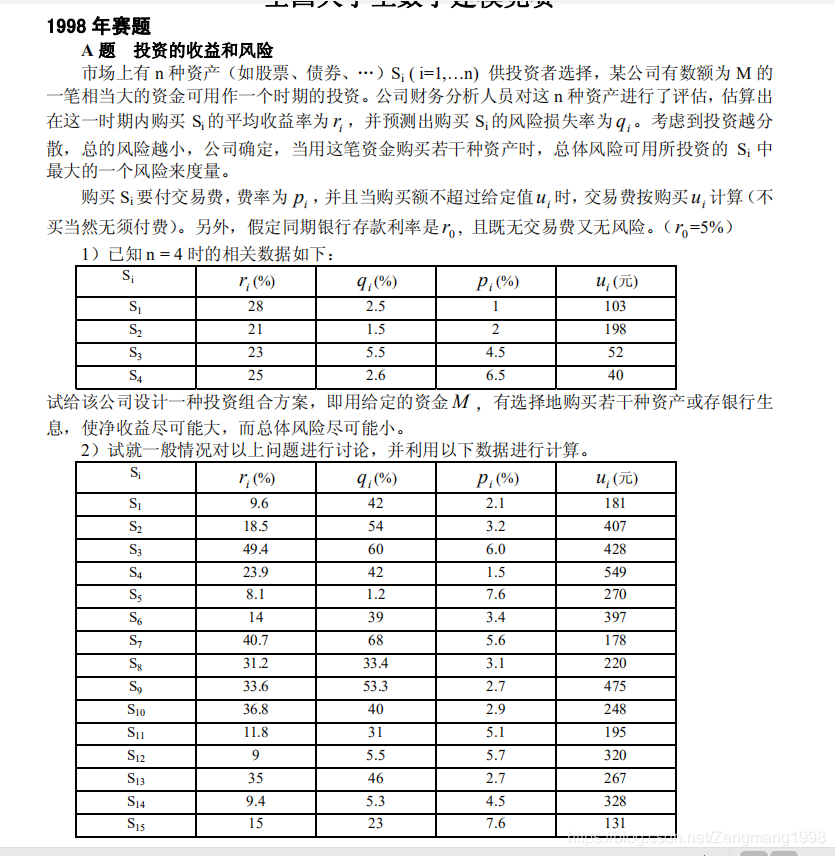
一段分析

 不难看出这是一道典型的组合优化题，根据题意，客户希望冒着最小的风险得到最大的收益，想要做这一点，就需要数学的帮助了。同时，问题1与问题2的求解模型是一样的，那么在给出模型的求解方案后，也需要有敏锐的观察力来分析出一些弦外之声，这可能需要结合当时的政策去做一些恰当的分析了（大胆yy）。

模型建立

 此处笔者珍惜键盘，偷懒直接用笔者的实验报告的内容来做阐述。

约定符号

多目标模型建立

 根据题意，利用金额M进行投资的过程中，主要需要满足的要求有以下两个：
1、获得尽可能的大的的收益；
2、承担尽可能小的风险损失。
根据题目的两个要求，笔者建立了出对应双目标规划数学模型为：

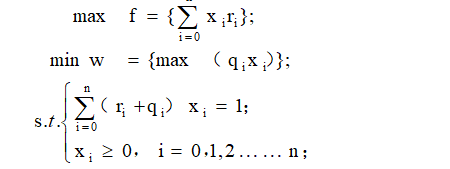
单目标模型建立

 我们不妨假设客户可以承受的最大风险率为a，则上述的双目标规划模型可以简化成建立成的单目标规划模型为：

模型求解

 此处模型建立完成后，笔者利用求解工具为matlab中的linprog函数，将问题中的相关资产数据代入其中进行求解。

问题1求解

 针对问题1，可得到对应单目标规划公式：

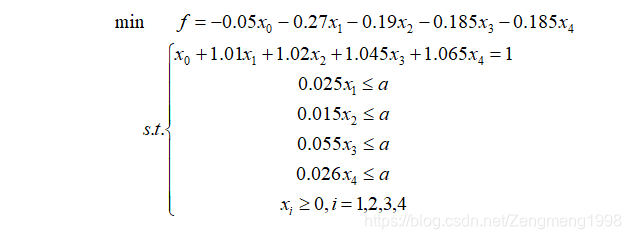
在求解过程中，笔者将的求解步长定为0.001，假设投资客户的理想承担风险在0-1之间，使用逐步迭代的方式，通过matlab工具实现求得如图1所示的与f的关系图像。

 根据图1不难看出，当投资客户的承担风险率与投资的回报率成在前一段区间成单调增的关系，当承担风险率在a=40%或以上时，客户可以获得回报率将趋于平稳且为最优，因此笔者取通过matlab求得所对应的最优解值为：
y =(0.0000 ,0.2400,0.4000 0.1091,0.2212);f=0.2019。即当在问题1条件下当客户的可承担风险率接近或大于40%时，所对应的投资组合为金额M中的24%投资资产1、40%用于投资资产2、10.91%用于投资资产3、22.1%用于投资资产4，可以得到最大为20.19%回报率。

问题2求解

 针对问题2，可得到单目标规划公式：

这里求解方式与问题1相同，笔者不做赘述，根据问题的所给的投资资产数据，
得到如图2所示的与f的关系图像。

 根据图2，我们可以得到f关于的变化规律，当客户的可承担风险率接近或大于60%时，可以得到的最大的回报，因此笔者取=0.6，代入模型中通过matlab求解得到：
y=（0.0000,0.0000,0.0000,0.9434,0.0000,0.0000,0.0000,0.0000,0.0000,0.0000,0.0000,0.0000,0.0000,0.0000,0.0000,0.0000);
f =0.4094;

注

 本文主要内容为建模过程的硬核求解部分，其余分析内容，笔者做出省略，请读者自行大胆yy，模型建立求解的过程的不足之处，望读者多加指正。其中代码笔者将分享至账号CSDN主页的资源与Github中，有进一步研究需求的读者可自行移步下载。

参考文献

[1]数模课程ppt
[2]陈云贤，证券投资论，北京工业大学出版社，北京，1992.
[3]程仕军，系统工程，极大化证券投资组合的投资收益率，1994.