WPBC乳腺癌数据集建模（Ⅱ）—预后诊断模型建立

前言

&#8195；经过前面的补充数据寻找、和原有数据的描述性统计与降维寻找对乳腺癌较大的10个指标的找寻工作后，笔者开始尝试建立关于乳腺癌的预后诊断模型。本文主要内容为模型的算法阐述与建模思路。其中不足，往读者多多指正。

模型假设

1、获取数据真实有效；
2、32项指标都对患者是否复发的一定影响因素；
……

建模过程

建模数据

1、原有数据经过一定的缺失值处理德等操作后得到数据集data_2其包括乳针吸细胞的的32特征（30项细胞特征、一项肿瘤特征、一项淋巴状态特征）194项数据，其是关于预后患者是否复发的数据；
2、补充数据集：在WPBC官网上找到的诊断数据，其共有30项特征（30项细胞特征）569例数据，为数据集data，其主要是判断患者是否肿瘤为恶性的数据。

• data数据一览

data.head()

	id	diagnosis	radius_mean	texture_mean	perimeter_mean	area_mean	smoothness_mean	compactness_mean	concavity_mean	concave points_mean	...	radius_worst	texture_worst	perimeter_worst	area_worst	smoothness_worst	compactness_worst	concavity_worst	concave points_worst	symmetry_worst	fractal_dimension_worst
0	842302	M	17.99	10.38	122.80	1001.0	0.11840	0.27760	0.3001	0.14710	...	25.38	17.33	184.60	2019.0	0.1622	0.6656	0.7119	0.2654	0.4601	0.11890
1	842517	M	20.57	17.77	132.90	1326.0	0.08474	0.07864	0.0869	0.07017	...	24.99	23.41	158.80	1956.0	0.1238	0.1866	0.2416	0.1860	0.2750	0.08902
2	84300903	M	19.69	21.25	130.00	1203.0	0.10960	0.15990	0.1974	0.12790	...	23.57	25.53	152.50	1709.0	0.1444	0.4245	0.4504	0.2430	0.3613	0.08758
3	84348301	M	11.42	20.38	77.58	386.1	0.14250	0.28390	0.2414	0.10520	...	14.91	26.50	98.87	567.7	0.2098	0.8663	0.6869	0.2575	0.6638	0.17300
4	84358402	M	20.29	14.34	135.10	1297.0	0.10030	0.13280	0.1980	0.10430	...	22.54	16.67	152.20	1575.0	0.1374	0.2050	0.4000	0.1625	0.2364	0.07678

5 rows × 32 columns

- data_2数据一览

data2.head()

	id	outcome	time	radius_mean	texture_mean	perimeter_mean	area_mean	smoothness_mean	compactness_mean	concavity_mean	...	perimeter_worst	area_worst	smoothness_worst	compactness_worst	concavity_worst	concave points_worst	symmetry_worst	fractal_dimension_worst	diameter of the excised tumor in centimeters	Lymph node status
0	119513	0	31	18.02	27.600000	117.50	1013.0	0.094890	0.103600	0.1086	...	139.70	1436.0	0.119500	0.192600	0.3140	0.1170	0.267700	0.08113	5.0	5
1	8423	0	61	17.99	22.300979	122.80	1001.0	0.118400	0.142642	0.3001	...	184.60	2019.0	0.162200	0.665600	0.7119	0.2654	0.460100	0.11890	3.0	2
2	842517	0	116	21.37	17.440000	137.50	1373.0	0.088360	0.118900	0.1255	...	159.10	1949.0	0.118800	0.344900	0.3414	0.2032	0.433400	0.09067	2.5	0
3	843483	0	123	11.42	20.380000	77.58	386.1	0.102774	0.142642	0.2414	...	98.87	567.7	0.143921	0.364567	0.6869	0.2575	0.322251	0.17300	2.0	0
4	843584	1	27	20.29	14.340000	135.10	1297.0	0.100300	0.132800	0.1980	...	152.20	1575.0	0.137400	0.205000	0.4000	0.1625	0.236400	0.07678	3.5	0

5 rows × 35 columns

思路构建（思路简化可用于摘要）

 在模型建立过程中尝试了SVM算法、kNN算法、通过PCA降维的SVM模型构建算法。
 笔者首先将原有的数据集data_2分成了两份：70%的数据作为训练集train用于模型训练；30%的数据作为测试集test用于模型的测试，计算模型的预测准确率。利用SVM算法建立得到的训练模型的预测准确率为79.66%，随后对模型进行如下改进：
1、在WPBC官网找到相关补充数据data（用于诊断检查者的肿瘤是否为阳性的数据集）对模型数据进行补充，希望通过增加训练数据的量来提高训练的准确率。笔者将data分为两份（做法与上同），得到模型预测准确率为高达98%，于是尝试将原数据进行列处理后将其放入模型中j进行模型测试，发现预后预测的准确率只有55.93% 反思得到：模型的data与data_2的并不完全相同，data数据集的指标相对data_2缺少两项，且其检测的针对人群亦不相同，data是检测者（想要知道自己是否患癌症）的人群数据，data_2针对的预后人群（检测其是否复发），因此，data的SVM诊断模型对data_2的诊断有一定的帮助，但不够理想。
2、更换算法，尝试利用KNN算法对数据data_2进行预测模型的建立。数据分法同上文，得到了KNN预后诊断模型，得到的预测准确率为76.27%，相对SVM的检测效果，仍不够理想。
3、利用PCA主成分分析算法对数据data_2进行降维处理后，通过SPSS提取出7个主成分，做训练的输入变量数据train_x,将其7个主成分数据列与诊断结果列（outcome）构成新的数据集data_PCA,数据分成两份（做法同上）得到的基于PCA降维后的SVM算法预后诊断模型的准确率为 84.75% 得到了一个相对较为理想的结果。作为最后的预后诊断模型。

算法模型简述

SVM支持向量机

支持向量机的思想是希望构建基于线性分类的思想的分类器算法。目的是希望构建一个超平面使得数据得到分类。

定义分离超平面：$w^{T}x+b=0$
定义几何间隔：$r=\frac{label(w^{T}x+b)}{||w|{|}_2}$
支持向量机目的就是分类的超平面到最近的点的几何最大，列出数学模型，经过推导，可把它转化成一个接凸二次规划问题：$$\min \frac{1}{2}||w|{|}^2$$ $$s.t.y_i(w^T{x}_i+b)\ge 1,i=1,2,..,m$$
利用用拉格朗日乘子法和KKT条件求解最优值（推导得到其对偶问题）：$$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2+\sum _{i=1}^m{\alpha }_i(-y_i(w^T{x}_i+b)+1)$$
具体的算法实现步骤：

• 线性分类的支持向量机算法（基于最大间隔）
  
• 非线性的SVM分类
  思想，利用核函数映射将非线性的数据映射成可进行线性分类的数据。
  
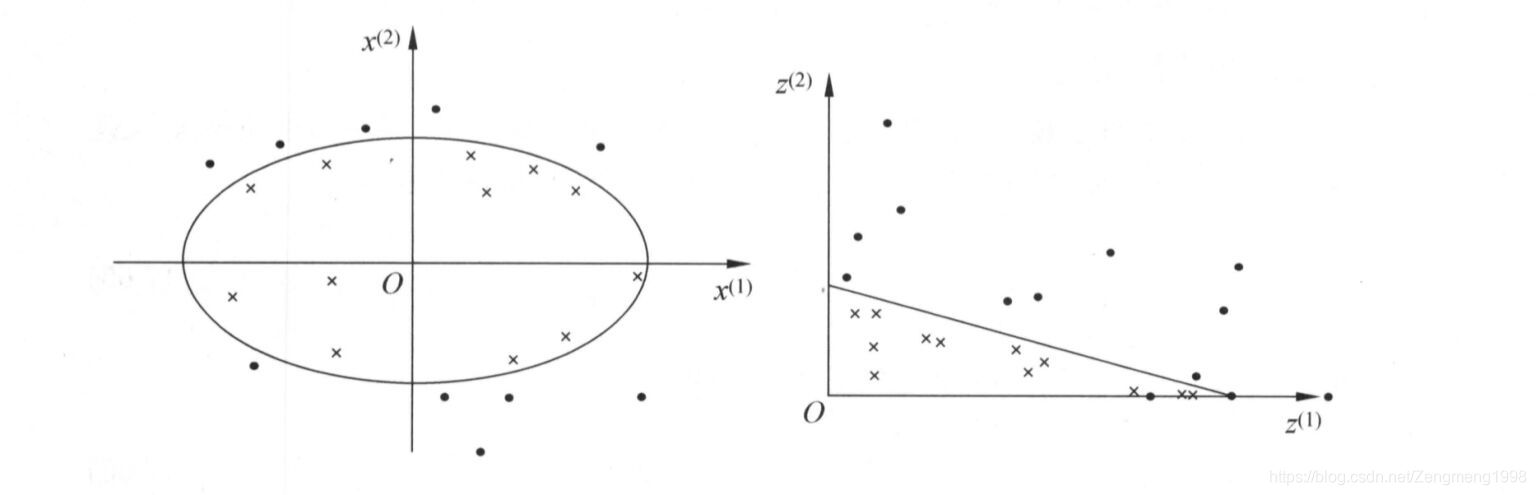
  算法实现步骤：
  

PCA主成分分析

是一种常用的降维算法。算法的实现步骤为：

KNN

基于距离聚类的分类算法，算法实现步骤为：

模型反思与推广

推广与优点：
1、补充数据得到的训练模型虽然在判断预后患者是否复发上效果不理想，但是其在诊断检测的肿瘤的良恶性上，是可以推广的；
2、在判断患者预后是否复发的应用上，基于PCA建立SVM复发诊断模型，具有一定的推广价值；
3、最后采用的算法为SVM算法，小样本训练集上能够得到比其它算法好很多的结果。SVM有优秀的泛化能力，这是是因为其本身的优化目标是结构化风险最小，而不是经验风险最小，因此，通过margin的概念，得到对数据分布的结构化描述，减低了对数据规模和数据分布的要求；
4、与传统的学习算法（如神经网络、模式识别）相比：SVM理论提供了一种避开高维空间的复杂性,直接用此空间的内积函数(既是核函数),再利用在线性可分的情况下的求解方法直接求解对应的高维空间的决策问题.当核函数已知,简化了高维空间问题的求解难度，相对于其他算法，具有较好的泛化推广能力。
不足：
1、误差的分类优化，比如与假阳性案例相比，自定义损失函数以惩罚假阴性更为重要（真实R但预测为N）案例，因为假阴性在真实环境中可能威胁生命，而假阳性只是相对烦恼；
2、我们预测错误的案例仍待深入研究。这将帮助我了解模型出了什么问题以及如何（如果可能）解决此问题；
3、训练数据量不够多，可以进一步找到相关的补充数据得到更加理想的结果；
4、求解函数的二次规划的过程中,SVM会占用大量的存储空间。

参考

李航.《统计学习方法》
SVM的优缺点