本文转自:http://blog.csdn.net/zhiyi_2012/article/details/12972813
在数学中,数量积(也称为内积、标量积、点积、点乘)是接受在实数R上的两个向量并返回一个实数值标量的二元运算。它是欧几里得空间的标准内积。
几何学定义与例子
两个向量a = [a1, a2,…, an]和b = [b1, b2,…, bn]的点积定义为:
这里的Σ指示总和符号。
例如,两个三维向量[1, 3, −5]和[4, −2, −1]的点积是
-
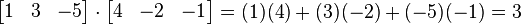 。
。
使用矩阵乘法并把(纵列)向量当作n×1 矩阵,点积还可以写为:
-
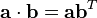 ,
,
这里的bT指示矩阵b的转置。
使用上面的例子,将一个1×3矩阵(就是行向量)乘以一个3×1向量得到结果(通过矩阵乘法的优势得到1×1矩阵也就是标量):
-
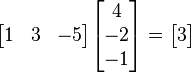 。
。
几何解释
在欧几里得空间中,点积可以直观地定义为
-
 ,
,
这里 |x| 表示x的范数(长度),θ表示两个向量之间的角度。
注意:点积的形式定义和这个定义不同;在形式定义中,a和b的夹角是通过上述等式定义的。
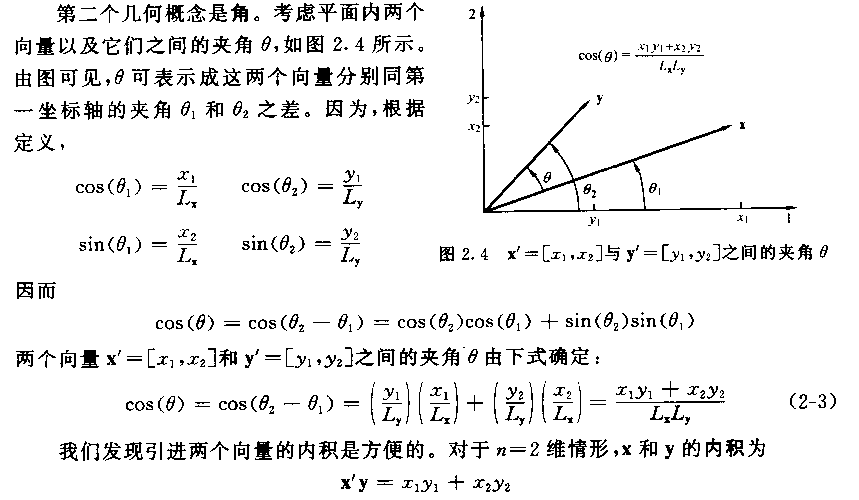
这样,两个互相垂直的向量的点积总是零。若a和b都是单位向量(长度为1),它们的点积就是它们的夹角的余弦。那么,给定两个向量,它们之间的夹角可以通过下列公式得到:
这个运算可以简单地理解为:在点积运算中,第一个向量投影到第二个向量上(这里,向量的顺序是不重要的,点积运算是可交换的),然后通过除以它们的标量长度来“标准化”。这样,这个分数一定是小于等于1的,可以简单地转化成一个角度值。
需要注意的是,点积的几何解释通常只适用于 (
( )。在高维空间,其他的域或模中,点积只有一个定义,那就是
)。在高维空间,其他的域或模中,点积只有一个定义,那就是
点积可以用来计算合力和功。若b为单位向量,则点积即为a在方向b的投影,即给出了力在这个方向上的分解。功即是力和位移的点积。
注:这样引出内积概念更加自然








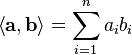
















 93万+
93万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








