机器学习 logistic回归的多分类（手写代码实现） python

最新推荐文章于 2024-08-24 18:06:30 发布

阿伦很努力

最新推荐文章于 2024-08-24 18:06:30 发布

阅读量533

点赞数 10

文章标签：机器学习回归分类

本文链接：https://blog.csdn.net/Zljhaodai/article/details/137679660

版权

本文介绍了如何使用LogisticRegression进行多分类问题的处理，重点讲解了softmax激活函数的运用以及参数优化的方法，包括梯度下降法的实现。作者还提到了利用极大似然估计法估计模型参数的可能性，并强调了矩阵计算在机器学习中的重要性，尤其是在np库的支持下。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

写在前面：

1.按课本所说，二分类可以使用sigmoid，softmax作为激活函数，扩展成多分类的情况

2.为了优化logistic回归模型的参数k和b，我采用梯度下降法（涉及学习率和迭代次数），该部分算法参考了网上的一些示例代码。

# 引用库，numpy库用于矩阵计算，sklearn库用于获取鸢尾花数据集，数据集划分
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
"""""
用于多分类的激活函数：softmax函数（将输入向量中的每个元素映射为一个处于 (0, 1) 之间的实数，并且所有元素的和等于 1。）
将一组实数转化为表示概率的值。
若是二分类，可考虑sigmoid函数
"""
def softmax(X):
    exps = np.exp(X - np.max(X)) # 第一步：将输入全部指数化（减去其中最大值，避免数据溢出）
    return exps / np.sum(exps, axis=1, keepdims=True) # 第二步：将每一行的每个元素除该行的和（保持原形状不变）

class LogisticRegression:
    # 模型参数，权值k，偏b，学习率（默认0.01，用于梯度下降），迭代次数（默认1000次）
    def __init__(self, learning_rate=0.01, num_iterations=1000):
        self.learning_rate = learning_rate
        self.num_iterations = num_iterations
        self.k = None
        self.b = None

    # 训练模型
    def fit(self, X, y):
        # 获取 样本数，特征数，类别数
        num_samples, num_features = X.shape
        num_classes = len(np.unique(y))

        # 初始化 权值k and 偏置b
        # k的形状（num_features*num_classes）
        # b的形状 (1*num_classes)
        self.k = np.zeros((num_features, num_classes))
        self.b = np.zeros(num_classes)

        # 梯度下降法，迭代1000次，优化模型参数
        for _ in range(self.num_iterations):

            # linear_model的形状是(num_samples*num_classes) 线性变换
            linear_model = np.dot(X, self.k) + self.b

            # 进softmax函数进行映射，得到该sample属于不同class的概率
            y_pred = softmax(linear_model)

            # error[i, j] 表示第 i 个样本在第 j 个类别上的误差值。
            # error 形状 (num_samples, num_classes)
            error = y_pred - np.eye(num_classes)[y]

            # 计算梯度
            dk= (1 / num_samples) * np.dot(X.T, error)
            db = (1 / num_samples) * np.sum(error, axis=0)

            # 更新参数
            self.k -= self.learning_rate * dk
            self.b -= self.learning_rate * db

    # 计算某sample属于个class的概率
    def predict_prob(self, X):
        linear_model = np.dot(X, self.k) + self.b
        y_pred = softmax(linear_model)
        return y_pred

    # 返回所有测试sample的预测类型
    def predict(self, X):
        y_pred_prob = self.predict_prob(X)
        y_pred = np.argmax(y_pred_prob, axis=1)
        return y_pred

# 加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=215275)

# 创建并训练 Logistic 回归模型
model = LogisticRegression()
model.fit(X_train, y_train)

# 在测试集上进行预测
predictions = model.predict(X_test)

# 打印预测结果 and 计算准确率
accuracy = 0
for i in range(len(predictions)):
    if predictions[i] == y_test[i]:
        accuracy += 1
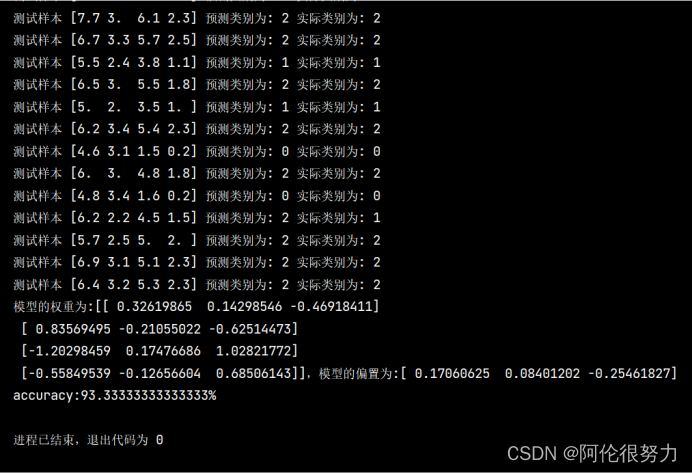
    print(f"测试样本 {X_test[i]} 预测类别为: {predictions[i]} 实际类别为: {y_test[i]}")
print(f"模型的权重为:{model.k}，模型的偏置为:{model.b}")
print(f"accuracy:{(accuracy/len(predictions)*100)}%")