题目设计背景
反射式系统没有色差,在很宽的波段范围内都可以保持良好的像质,光学系统中的光路可以折叠,系统透过率高,热稳定性强,不易受到辐射的影响。镜片可以做得很大,且容易实现轻量化。离轴三反系统常用于空间相机、遥感系统等。
系统设计要求

共轴系统初始参数计算

将主镜与次镜、次镜与三镜、三镜与像面之间的距离分别设置为d1=-130mm、d2=130mm、l3'=-130mm。
根据方程组计算初始结构。

其中Φ是系统总光焦度(焦距倒数),![]() ,c1、c2、c3是三个球面的待求曲率(半径的倒数)。
,c1、c2、c3是三个球面的待求曲率(半径的倒数)。
整理得

我使用卡西欧计算器解方程式功能计算求得方程1,进而求出方程式2,3的解。计算结果如下:
 或
或 
进而,根据下示公式计算![]() 、
、![]() 、
、![]() 、
、![]() 。
。

计算结果如下:
![]() ,其中
,其中![]() 不符合要求,因此舍去这一组结果。
不符合要求,因此舍去这一组结果。
另一组计算结果如下:

下面继续求非球面系数。

令![]() ,我在Matlab利用代码求解,代码与运行结果如下:
,我在Matlab利用代码求解,代码与运行结果如下:
a1 = 0.4873380445;
a2 = 1.947118885;
b1 = 1.110698735;
b2 = 0.4864206763;
syms e12 e22 e32
eqns = [e12 == 1 + 1/(b1^3*b2^3)*(e22*a1*b2^3*(1+b1)^3 - e32*a1*a2*(1+b2)^3-a1*b2^3*(1+b1)*(1-b1)^2+a1*a2*(1+b2)*(1-b2)^2);
e22*(a1-1)*b2^3*(1+b1)^3-e32*(a2*(a1-1)+b1*(1-a2))*(1+b2)^3 == (a1-1)*b2^3*(1+b1)*(1-b1)^2-(a2*(a1-1)+b1*(1-a2))*(1+b2)*(1-b2)^2-2*b1*b2;
e22*b2*(a1-1)^2*(1+b1)^3/(4*a1*b1^2)-e32*(a2*(a1-1)+b1*(1-a2))^2*(1+b2)^3/(4*a1*a2*b1^2*b2^2)== b2*(a1-1)^2*(1+b1)*(1-b1)^2/(4*a1*b1^2)-(a2*(a1-1)+b1*(1-a2))^2*(1+b2)*(1-b2)^2/(4*a1*a2*b1^2*b2^2)-b2*(a1-1)*(1+b1)*(1-b1)/(a1*b1)-(a2*(a1-1)+b1*(1-a2))*(1+b2)*(1-b2)/(a1*a2*b1*b2)-b1*b2+b2*(1+b1)/a1-(1+b2)/(a1*a2)];
vars = [e12 e22 e32];
[e12, e22, e32] = solve(eqns, vars);
e12 = double(e12);
e22 = double(e22);
e32 = double(e32);
最终全部初始结构计算结果如下:

离轴系统与ZEMAX设计
法1(2×3视场点)
首先将计算好的初始结构输入至ZEMAX中,将系统孔径选为入瞳直径,设定为90mm,设定波长为8、10、12μm,10μm为中心波长。接下来设定视场,选定矩形视场,由于x方向视场对称,只取0-2°,y方向-1.5-1.5°视场。由于需要设置视场离轴,将y方向中心视场设为15°,那么最终设置好的视场如下图所示。

接下来对经过视场离轴后的系统进行优化。优化主要通过REAY和REAX操作数控制像高完成。
首先计算Y方向像高。Y方向视场为13.5-16.5°,焦距137mm,那么Y方向像高
![]()
X方向视场为0-2°,焦距137mm,那么X方向像高
![]()
设置X、Y方向像高,配合DIFF操作数计算实际像高,并用OPGT、OPLT控制实际像高与理想像高的差距只在10μm范围内。优化评价函数设置为 “波前-RMS-质心”。将全部半径设置为变量,将主镜与三镜的厚度设为变量,将次镜的厚度的设为 “拾取”,拾取为主镜厚度的相反数。将圆锥系数与偶次非球面的6-8阶系数设置为变量。进行优化。
如图所示。 可以发现经过优化后的系统基本已满足设计要求。





法2(3×3视场点)
法2与法1思路基本一致,只是在视场点数量的设定上有一点改变。如下图所示。

这种方法在优化过程中,设置像高操作数时,是取相邻视场在像面上的像高值进行优化,而法1选定的是x、y视场在像面上最大视场与最小视场上的像高进行优化的。法2的优化方式更加准确、细致。

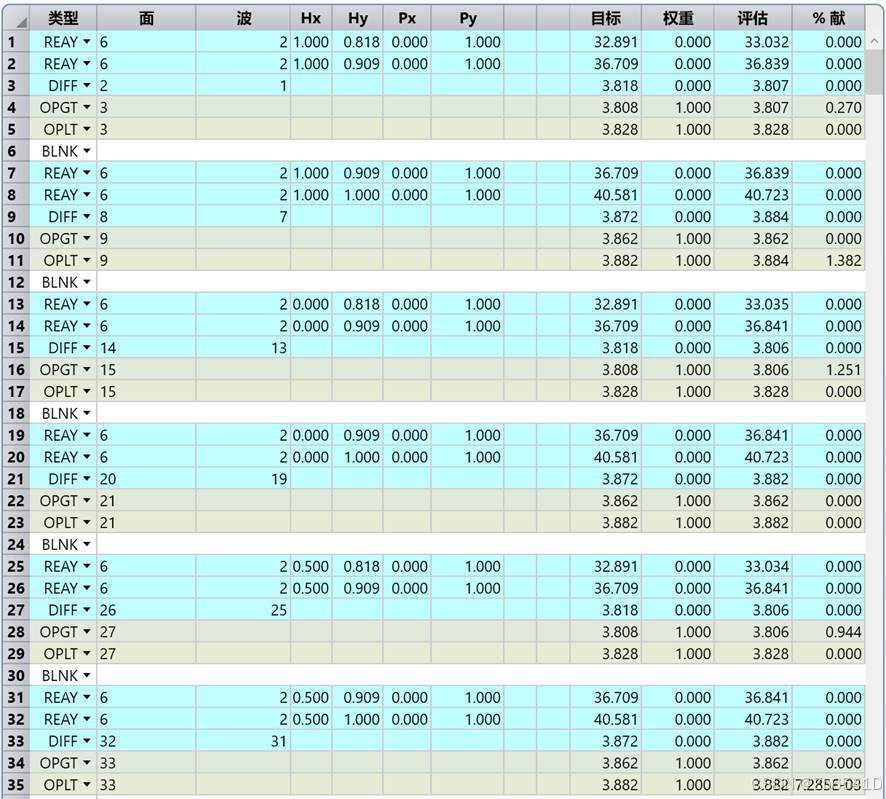

然而这样优化后,视场遮拦较严重,如下图所示。

因此我改变了自变量,将主镜的厚度改为固定变量,由于次镜厚度拾取自主镜,因此次镜厚度也为固定变量,保持其他设置不变。执行优化,优化后效果较好,但像面处光线与次镜上的光线距离较近。因此在像面前添加坐标断点,将倾斜X与倾斜Y设为变量,同时重新添加主镜厚度为变量。进行优化,优化后效果较好,且均已达到各个设计要求。
最终系统设计结果




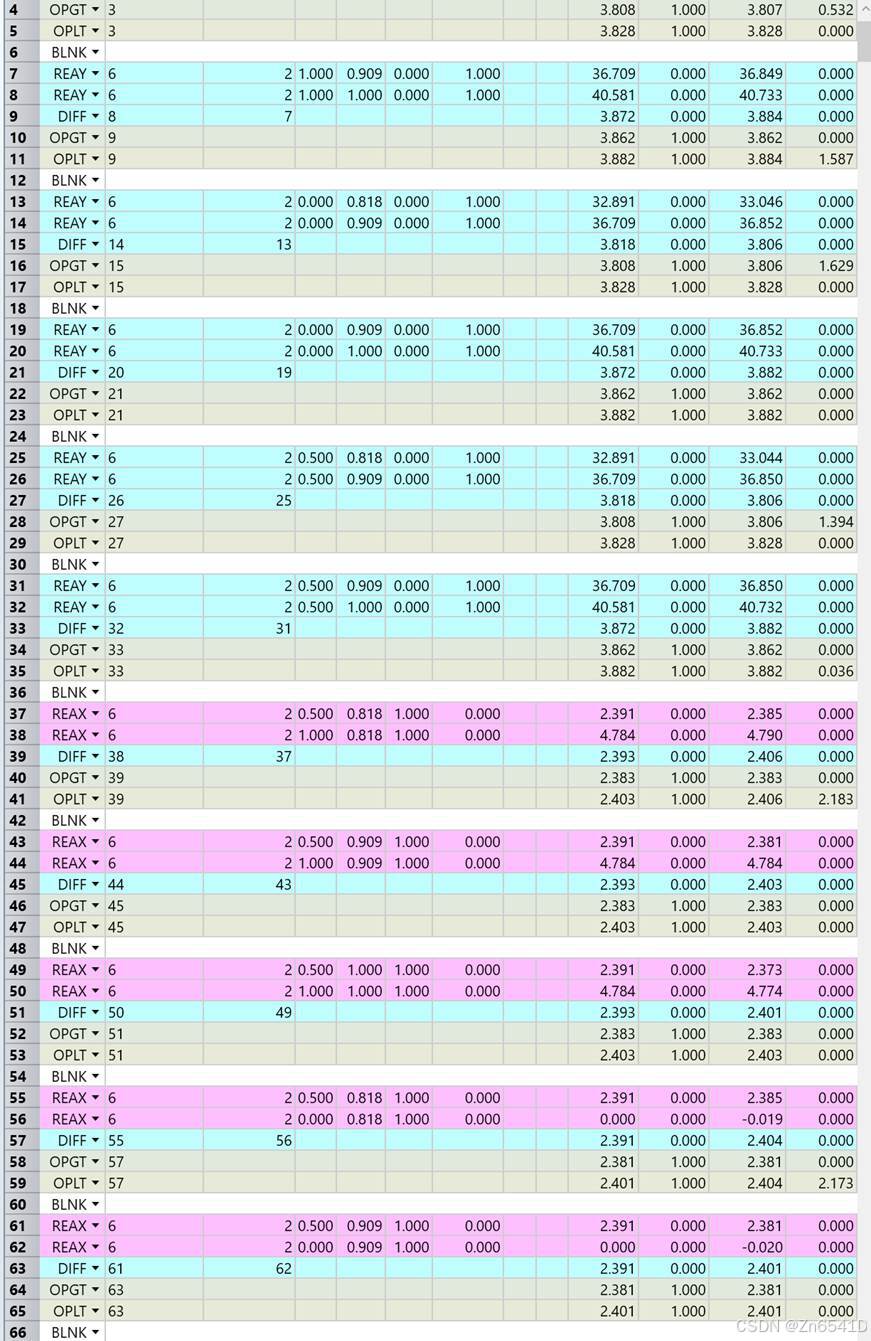



点列图已经优化至半径最小状态。通过操作数88-106的DIFF的评估值,可以看出全视场实际像高与理想像高相差上下浮动在25μm范围内,即全视场畸变已控制在40μm内。通过观察MTF曲线,黑色线为衍射极限,可以看到在空间频率25时,MTF曲线已基本接近衍射极限。

























 3513
3513

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








