人工智能学习教程笔记-09：浅层神经网络

文章部分内容参考自https://captainbed.net、https://captainbed.vip/1-3-3/

浅层神经网络

浅层神经网络的计算流程同单神经元网络几乎一样，只不过更为复杂而已。

浅层神经网络的向量化

向量化这种用法在人工智能编程中几乎无处不在，可以说我们在人工智能编程中大多数情况下处理的最小数据单元就是向量，而我们编写多神经元网络就会用到比向量更高一个级别的数据单元——矩阵。所以说浅层神经网络的向量化实际上是矩阵化。

以下图的浅层神经网络为例：

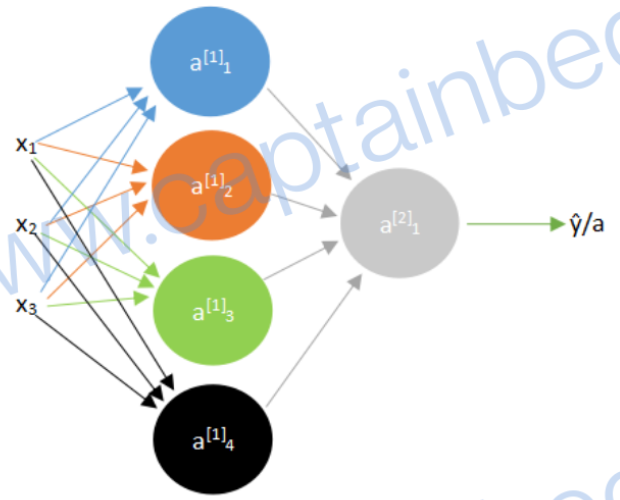
上标表示第几层，下标表示第几行，其最初的形式如下：

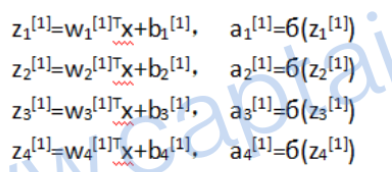
我们知道，每一个权重值$w_i^{[j]T}$都是一个行向量，其中有对应$x_1～x_3$的三个值，此时我们有四个这样的行向量，就组成了一个$4\ast 3$的矩阵。向量的形式如下所示：

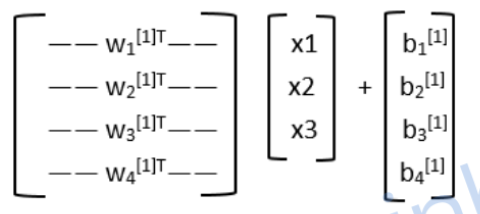
tips：看不懂就去复习一下线性代数矩阵乘法

我们省去下标，按照矩阵的形式还可以简写为：

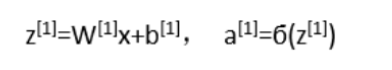
第二层同理：

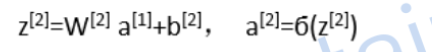
然而考虑到我们训练神经网络往往需要很多训练样本，写法如下（上标的括号中的数表示第i个训练样本）：

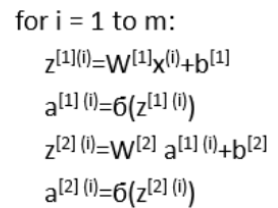
之前在向量化中提到我们一般不推荐使用for循环，要尽可能使用向量化来替代for循环。我们把每一个样本的特征向量x也组合成一个矩阵，如下所示：

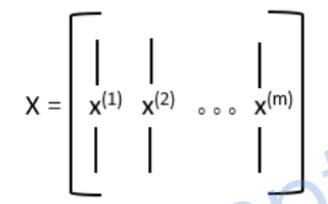
这样以来，上面for循环可以写成如下矩阵乘法的形式（如果看不明白去复习一下矩阵乘法）：

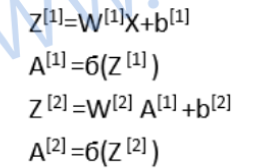
其中的Z和A都是矩阵，矩阵中的每一个列向量对应一个训练样本（例如$z^{[1](2)}$就是第二个样本第一层的z）：

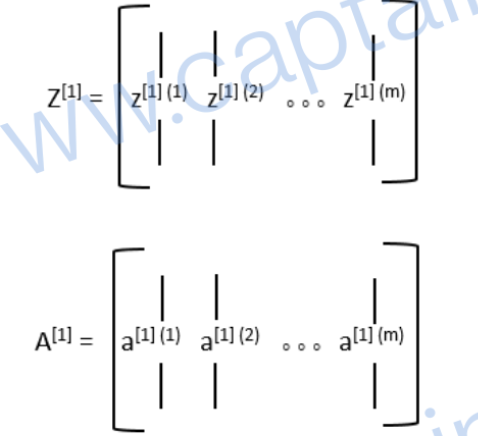
浅层神经网络的损失函数

我们通过下面的式子求出多神经元神经网络的损失函数，相比于单神经元神经网络的损失函数仅仅多了A的上标，毕竟每层都要求一遍损失函数：

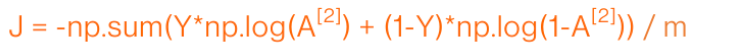
⭐浅层神经网络的反向传播

反向传播（Back propagation）可以说已经是神经网络模型的标配了，其求解偏导数的效率是最高的。

浅层神经网络计算偏导数的思路和单神经元网络是一样的，我们先计算出最后一层的偏导数，再反着往前推，计算前一层的，再求前一层的偏导数，以此类推。

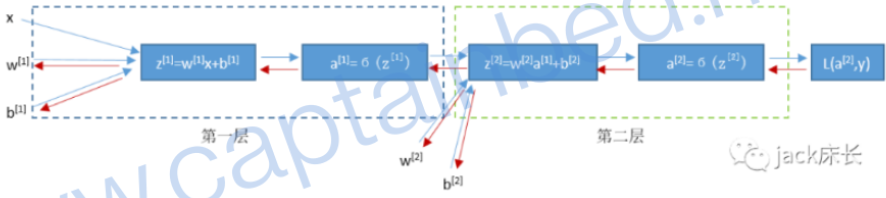
求第二层偏导数

第二层偏导数公式如下，同单神经元网络是一样的（单样本），可以把$a^{[1]}$看作是$x$：

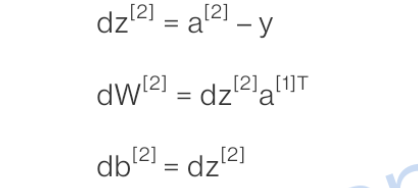
⭐️求第一层偏导数

第一层的偏导数与第二层就不一样了，因为第二层直接与损失函数相邻，而第一层与损失函数没有直接的联系。
💡可以看一下上面的损失函数用的是最后一层的$a^{[2]}$​​来求的，中间的层仅仅用来过渡。

我们要通过链式求导法则来求第一层的偏导数：

$\{\begin{array}{ll}\frac{\partial L}{\partial z^{[1]}}=\frac{\partial L}{\partial a^{[1]}}\frac{\partial a^{[1]}}{\partial z^{[1]}}& \\ \frac{\partial L}{\partial a^{[1]}}=\frac{\partial L}{\partial z^{[2]}}\frac{\partial z^{[2]}}{\partial a^{[1]}}& \end{array}$

而$\frac{\partial z^{[2]}}{\partial a^{[1]}}$我们前面已经求出来了，最终推导结果如下：

$\frac{\partial L}{\partial a^{[1]}}=W^{[2]T}\frac{\partial L}{\partial z^{[2]}}$

$\frac{\partial L}{\partial z^{[1]}}=W^{[2]T}\ast \frac{\partial L}{\partial z^{[2]}}\frac{\partial g^{[1]}}{\partial z^{[1]}}$（$g^{[1]}$表示sigmoid激活函数，其实还可以用其他激活函数）

得出$d{z}^{[1]}$后，$d{w}^{[1]}$以及$d{b}^{[1]}$就可以通过$d{z}^{[1]}$求出来了，公式与单神经元网络是一样的：

$d{w}^{[1]}=d{z}^{[1]}{X}^T$

$d{b}^{[1]}=d{z}^{[1]}$​

多训练样本时

多训练样本时我们要通过向量化将向量变为矩阵（小写字母变大写），来提高运算效率。而且还要除以样本总数m来求平均值。

最后一个np.sum()的参数不同，是因为第一层不再只有一个神经元了，$d{z}^{[1]}$的维度是$(n^{[1]},m)$（$n^{[1]}$是第一层神经元的个数，m是训练样本个数），我们需要将每一个神经元对应的训练样本的结果参数累加起来：

asix=1的作用就是让sum只累加每一行中的所有元素。而keepdims是为了防止sum的输出结果变成$(n^{[1]},)$这样的形式，我们需要的形式是$(n^{[1]},1)$。