MMD ：maximum mean discrepancy

MMD：maximum mean discrepancy。最大平均差异。最先提出的时候用于双样本的检测（two-sample test）问题，用于判断两个分布p和q是否相同。它的基本假设是：如果对于所有以分布生成的样本空间为输入的函数f，如果两个分布生成的足够多的样本在f上的对应的像的均值都相等，那么那么可以认为这两个分布是同一个分布。现在一般用于度量两个分布之间的相似性。在[1]中从任意空间到RKHS上介绍了MMD的计算，这里根据这个顺序来介绍。
1.任意函数空间（arbitary function space）的MMD
具体而言，基于MMD（maximize mean discrepancy）的统计检验方法是指下面的方式：基于两个分布的样本，通过寻找在样本空间上的连续函数f，求不同分布的样本在f上的函数值的均值，通过把两个均值作差可以得到两个分布对应于f的mean discrepancy。寻找一个f使得这个mean discrepancy有最大值，就得到了MMD。最后取MMD作为检验统计量（test statistic），从而判断两个分布是否相同。如果这个值足够小，就认为两个分布相同，否则就认为它们不相同。同时这个值也用来判断两个分布之间的相似程度。如果用F表示一个在样本空间上的连续函数集，那么MMD可以用下面的式子表示：

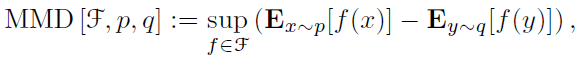
假设X和Y分别是从分布p和q通过独立同分布(iid)采样得到的两个数据集，数据集的大小分别为m和n。基于X和Y可以得到MMD的经验估计(empirical estimate)为：