一、用神经网络进行监督学习

夏天&菊次郎

已于 2024-04-13 10:03:26 修改

阅读量1.5k

点赞数 40

分类专栏：神经网络与深度学习文章标签：神经网络深度学习机器学习

于 2024-03-07 22:01:27 首次发布

本文链接：https://blog.csdn.net/a1171171/article/details/136547304

版权

神经网络与深度学习专栏收录该内容

4 篇文章 0 订阅

订阅专栏

本文详细介绍了监督学习中的回归与分类任务，包括线性回归、梯度下降法在logistic回归中的应用，以及向量化技术的意义。通过实例阐述了损失函数和代价函数的概念，并讨论了学习率对优化过程的影响。

摘要由CSDN通过智能技术生成

监督学习的两个任务：回归与分类

回归：预测一个具体的数值输出

分类：预测离散的输出

（一）logistic回归的损失函数与代价函数

一、符号表示

m:训练样本的数量

x:输入特征

y:输出变量（要预测的目标变量），真实值

（x,y）表示一个训练样本

$(x^{(i)},y^{(i)})$ 表示第i个训练样本

二、二分类算法

在识别一幅图像中是否有猫时，输出的结果有两种：有（用1表示），无（用0表示）。

假如图像大小为64*64*3=12288，

定义输入特征 $x=\begin{bmatrix} p_1& p_2 & ...& p_{12288} \end{bmatrix}^{T}$ ， $x$ 是一个 $n_{x}$ =12288维的向量， $x\in \mathbb{R}^{n_{x}}$ ,输出变量 $y\in\left \{ 0 ,1\right \}$

m个训练样本集： $\left \{ \left ( x^{(1)},y^{(1)} \right ),......,\left ( x^{(m)},y^{(m)} \right ) \right \}$

令输入特征为 $X=\left [ x^{(1)}, x^{(2)},...,x^{(m)}\right ]_{n_{x}\ast m},X \in \mathbb{R}^{n_{x}*m}$

输出为 $Y=\left [ y^{(1)}, y^{(2)},..., y^{(m)} \right ]_{1*m},Y \in \mathbb{R}^{1*m}$

三、线性回归

表达式： $h(x)=\theta _{0}+\theta _{1}x$

参数 $\theta _{0}$ 、 $\theta _{1}$ 该如何选择呢？

定义一个代价函数: $J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^{m}(h(x^{(i)})-y^{(i)})^{2}$

也称平方误差函数，使函数最小化，得到最优的参数 $\theta _{0}$ 、 $\theta _{1}$ 的值

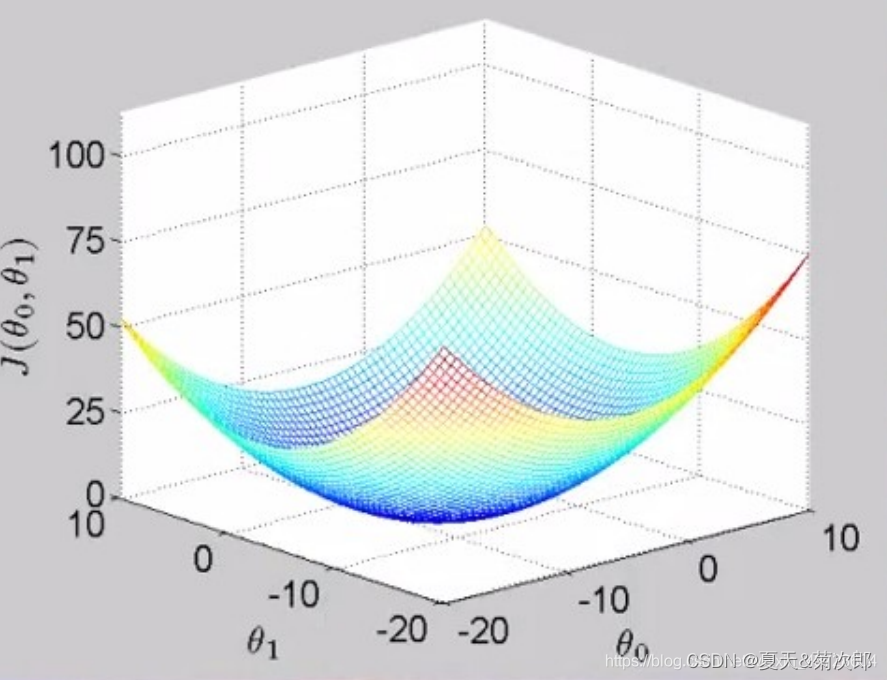
等高线：

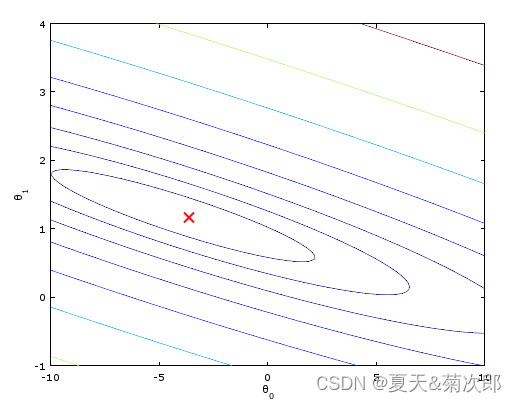
怎么最小化代价函数 $J(\theta_0,\theta_1)$ 呢？

四、梯度下降法

重复以下过程直到收敛：

$\theta_j=\theta_j-\alpha*\frac{\partial J(\theta_0,\theta_1)}{\partial \theta_ j} \qquad(j=0,1)$

为保证所有参数同步更新，采用如下办法：

$temp0=\theta_0-\alpha*\frac{\partial J(\theta_0,\theta_1)}{\partial \theta_0}$

$temp1=\theta_1-\alpha*\frac{\partial J(\theta_0,\theta_1)}{\partial \theta_1}$

$\theta _{0}=temp0$

$\theta _{1}=temp1$

其中 $\alpha$ 代表学习率，介于0-1之间，控制着步长， $\alpha$ 值的选取很重要。当 $\alpha$ 太小时，如下左图，每次只能移动一点点，需要很多步才能找到局部最低点，当 $\alpha$ 太大时，如下右图，可能会越过局部最低点，甚至可能离最低点越来越远，导致无法收敛。

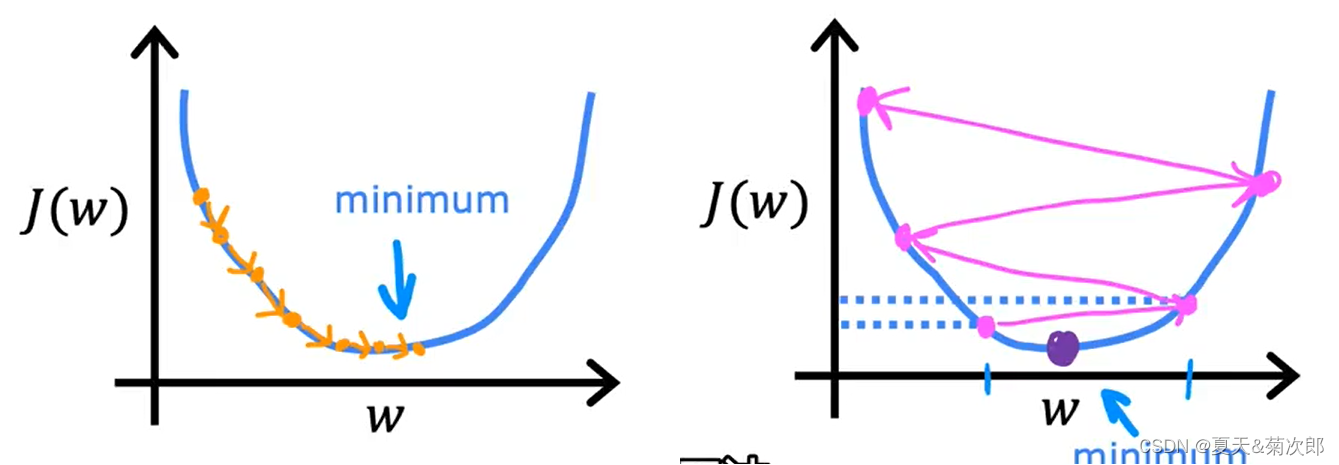
注意，当逐步接近最小值点时，导数值会逐步变小，因此移动的步幅也会变小

五、logistic回归

给定 x，预测值 $\hat{y}=P(y=1|x)\approx y,0\leq \hat{y}\leq 1,x\epsilon R^{n_{x}}$

参数： $\omega \epsilon R^{n_{x}},\quad b\epsilon R$

输出： $\hat y=\sigma (\omega ^{T}x+b)=\sigma (z)=\frac{1}{1+e^{-z}}$ (令 $z=\omega ^{T}x+b$ )

$\sigma$ 函数的作用是为了保证 $\hat y$ 在0-1之间， $\sigma$ 函数图像如下图所示：

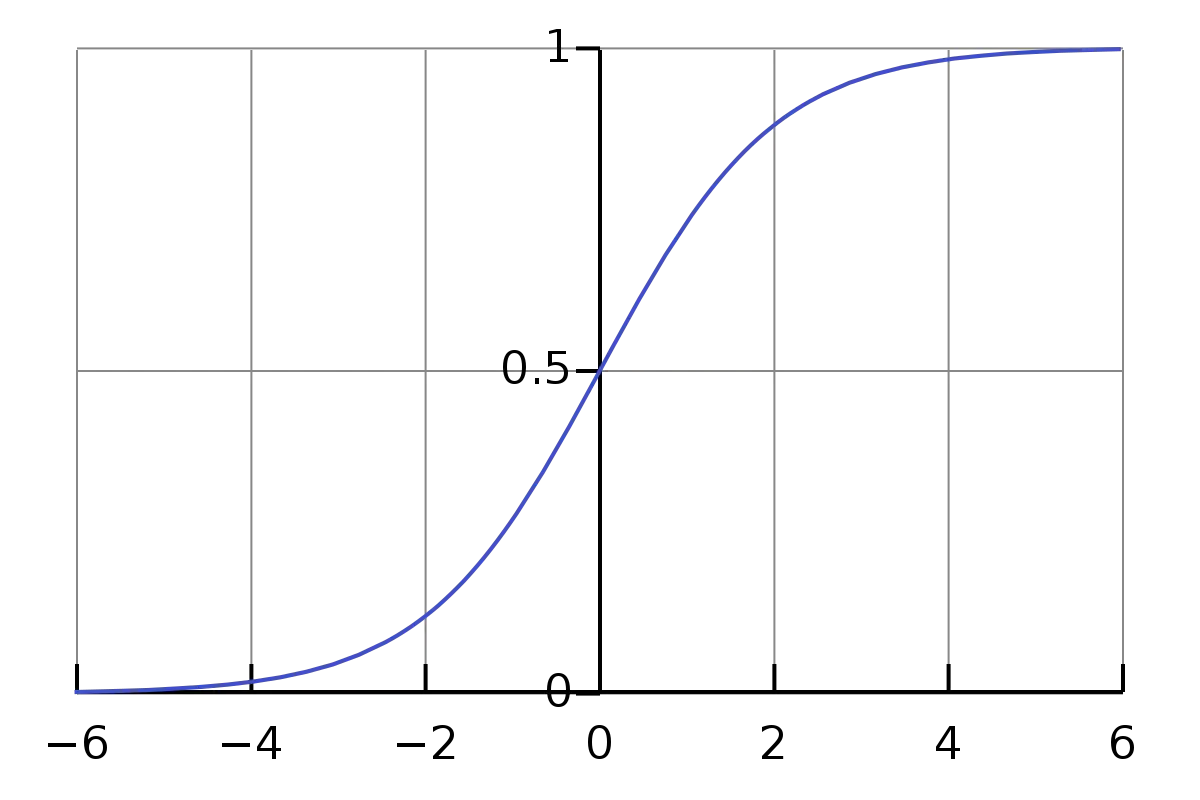
logistic回归的任务：通过代价函数，优化 $\omega ,b$

（一）logistic回归的损失函数与代价函数

1.损失函数（误差函数）

$L(\hat y,y)=-(ylog \hat y+(1-y)log(1-\hat y))$

当y=1时， $L(\hat y,y)=-log \hat y$ ,L 越小， $\hat y$ 越大，越接近y（=1）

当y=0时， $L(\hat y,y)=-log (1- \hat y)$ ,L 越小， $\hat y$ 越小，越接近y（=0）

注：损失函数是在单个训练样本中定义的，是凸函数，可以用梯度下降法进行优化。

2.代价函数(成本函数)

代价函数是在整个训练集上定义的，用来衡量在所有样本上的表现

$J(\omega ,b)=\frac{1}{m}\sum_{i=1}^{m}L(\hat y^{(i)},y^{(i)})$

$=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log \hat y^{(i)}+(1-y^{(i)})log(1-\hat y^{(i)})]$

（二）logistic回归中的梯度下降法

1.单样本、两个输入特征的情况

正向过程：

$\left\{\begin{matrix} z=w_{1}x_{1}+w_{2}x_{2}+b\\a=\hat y=g(z)=\sigma (z) \\L(a,y)=-(yloga+(1-y)log(1-a)) \end{matrix}\right.$

反向传播：

$\left\{\begin{matrix} da=\frac{\partial L}{\partial a}=-\frac{y}{a}+\frac{1-y}{1-a}\\ \\dz=\frac{\partial L}{\partial z}=\frac{\partial L}{\partial a}*\frac{\partial a}{\partial z}=a-y\\ \\dw=\frac{\partial L}{\partial w}=x*dz\end{matrix}\right.$

$dw_{1}=\frac{\partial L}{\partial w_{1}}=x_{1}*dz,dw_{2}=\frac{\partial L}{\partial w_{2}}=x_{2}*dz .db=dz$

更新w1,w2,b：

$w_{1}=w_{1}-\alpha *dw_{1}, w_{2}=w_{2}-\alpha *dw_{2}, b=b-\alpha *db$

2.m个样本、nx个输入特征的情况的情况

$J(\omega ,b)=\frac{1}{m}\sum_{i=1}^{m}L(a^{(i)},y)$

$=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log a^{(i)}+(1-y^{(i)})log(1-a^{(i)})]$

$a^{(i)}=\hat{y}^{(i)}=\sigma (z^{(i)})=\sigma (\omega ^{T}x^{(i)}+b)$

$\frac{\partial J(w,b) }{\partial w_1}=\frac{1}{m}\sum_{i=1}^{m}\frac{\partial L(a^{(i)},y^{(i)}) }{\partial w_1} \, \, \, (\frac{\partial L(a^{(i)},y^{(i)}) }{\partial w_1}=dw_{1}^{(i)})$

初始化： $J=0,dw_{1}=0,...,dw_{n_x}=0,db=0$

一次梯度下降：

For i=1 to m :

$z^{(i)}=w^{T}x^{(i)}+b$

$a^{(i)}=\sigma (z^{(i)})$

$J+=-[y^{(i)}log a^{(i)}+(1-y^{(i)})log(1-a^{(i)})]$

$dz^{(i)}=a^{(i)}-y^{(i)}$

$\left\{\begin{matrix} dw_1+=x_{1}^{(i)}dz^{(i)}\\ dw_2+=x_{2}^{(i)}dz^{(i)} \\ ...\\ dw_{n_x}+=x_{n_x}^{(i)}dz^{(i)} \end{matrix}\right.$

$db+=dz^{(i)}$

$J/=m$

$\left\{\begin{matrix} dw_1/=m \\ ... \\ dw_{n_x}/=m \end{matrix}\right.$

$db/=m$

$\left\{\begin{matrix} w_1=w_1-\alpha dw_1\\ ...\\w_{n_x}=w_{n_x}-\alpha dw_{n_x} \end{matrix}\right.$

六、向量化

向量化的意义

$\overrightarrow{a}=(1,2,3),\overrightarrow{b}=(4,5,6),c=0$ ，向量a与b相乘

method 1:for循环

a=[1,2,3]
b=[4,5,6]
c=0
for i in range(3):
    c+=a[i]*b[i]
print c

method 2:内置函数np.dot(a,b)

import numpy as np
a=[1,2,3]
b=[4,5,6]
c=np.dot(a,b)

使用内置函数计算比for循环速度快得多，因此在设计新网络时，或只是回归时尽量避免使用for循环。

夏天&菊次郎

关注

40
点赞
踩
36

收藏

觉得还不错? 一键收藏
0
评论
一、用神经网络进行监督学习

监督学习的两个任务：回归与分类回归：预测一个具体的输出分类：预测的输出。
复制链接

扫一扫

专栏目录

一、用神经网络进行监督学习

一、符号表示

二、二分类算法

三、线性回归

四、梯度下降法

五、logistic回归

（一）logistic回归的损失函数与代价函数

1.损失函数（误差函数）

2.代价函数(成本函数)

（二）logistic回归中的梯度下降法

1.单样本、两个输入特征的情况

2.m个样本、nx个输入特征的情况的情况

六、向量化

向量化的意义

“相关推荐”对你有帮助么？