0 前言
🙋欢迎光临我的博客!我衷心希望这里的分享能够对你有所帮助。祝愿你拥有美好的一天!☀️☀️☀️今天,我想与大家分享我在研究生一年级时完成的现代信号处理仿真课程的大作业之一。如果其中有任何不足之处,还请大家多多包涵。
目录
✈️0 前言
✈️1 问题背景
☁️1.1 建立算法
☁️1.3 通过仿真,分析模型参数及初始值对卡尔曼滤波递推算法的影响。
✈️2 实验目的
✈️3 实验原理
✈️4 实验过程
✈️参考资料与文献
1 问题背景
假设雷达对在三维空间作匀加速运动的目标进行观测,测量值为目标的三维坐标(x,y,z),对目标的距离、速度、加速度进行估计。运动目标的初始位置为,初始速度为
,加速度为
,目标三维的加加速度都是均值为0的高斯噪声,均方差都是
。雷达对目标的三维距离观测噪声都是均值为0的高斯噪声,均方差都是30m。建立雷达对目标的跟踪算法,并进行仿真分析,给出仿真分析结果。
1.1 建立算法
(1)建立状态方程及观测方程;
(2)给出卡尔曼滤波递推算法公式;
(3)确定模型参数及初始值。
1.2 编程仿真计算
(1)模拟目标真实运动轨迹;
(2)形成观测数据;
(3)递推估计目标三维距离、速度及加速度;
(4)计算估计误差。
1.3 通过仿真,分析模型参数及初始值对卡尔曼滤波递推算法的影响。
2 实验目的
1.掌握卡尔曼滤波的准则、基本原理和解决问题的基本思路;
2.加深对信号模型、卡尔曼滤波及参数物理意义的理解;
3.熟练掌握卡尔曼滤波算法的基本特点及递推流程;
4.分析讨论实际状态值和估计值的误差。
3 实验原理
卡尔曼滤波是一种效率高的最优估计算法,能够从一系列的不完全及包含噪声的测量中,估计动态系统的状态,广泛应用于导航、控制、雷达、遥感遥测及计算机图像处理等领域。
卡尔曼滤波是以线性最小均方误差为准则的最佳递归滤波器,它根据前一个估计值和最近一个观察数据来估计状态变量(信号)的当前值。它以状态方程和观测方程为信号模型(系统模型),采用递推方法进行估计,它的解是以状态变量估计值的形式给出。
卡尔曼滤波的信号模型是用状态方程和观测方程来表示的,因此设计卡尔曼滤波器要求已知状态方程、观测方程和相关的统计特性。它不需要知道全部过去的数据,只需利用当前的观测数据,采用递推的计算方法估计状态变量。它既可以用于平稳和非平稳随机过程,同时也可以应用于时不变和时变系统,因而被广泛应用。
由于公式太多,涉及到公式部分我将用图片替代,如果图片模糊,请向我告知😊


4 实验过程



仿真实验结果如图5.1~图5.4所示。
由图5.1可知,卡尔曼滤波能够很好的估计出运动目标的位置信息,对三维空间中的运动目标跟踪效果比较好。
由图5.2-5.5可知,尽管模型滤波之后误差相对有所降低,但是仍然出现大幅度的震荡效果,不能有效的趋于稳态。然而从系统增益来看,又能很快趋于平稳值,说明滤波器是趋于稳态的。因此卡尔曼滤波也是趋于稳态的。
对于模型跟踪误差存在震荡误差的问题,猜测是系统过程噪声和观测噪声过大造成,为进一步对探究模型的稳定性,将减小系统噪声,进一步对模型进行模拟。
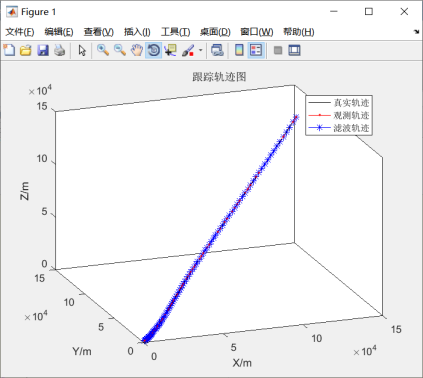
图5.1 卡尔曼滤波结果
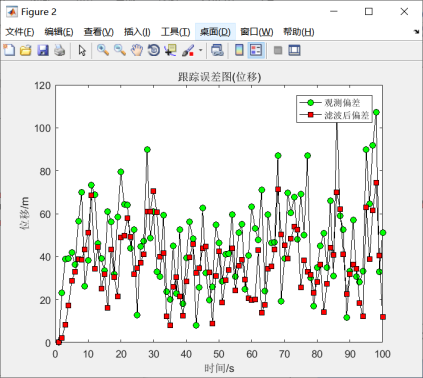
图5.2 位移跟踪误差结果
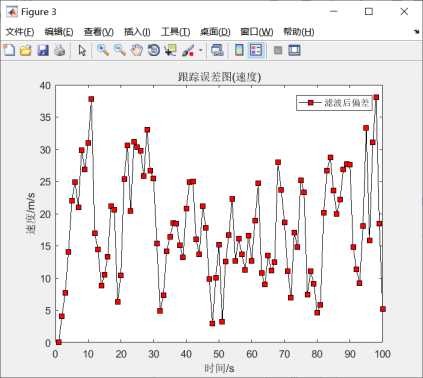
图5.3 速度跟踪误差结果
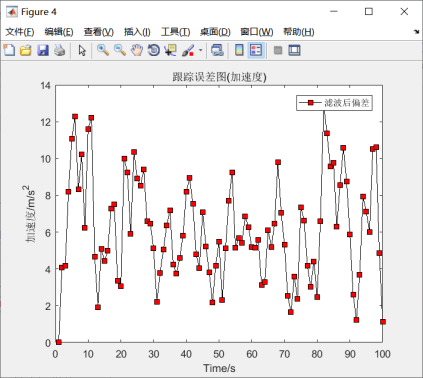
图5.4 加速度跟踪误差结果
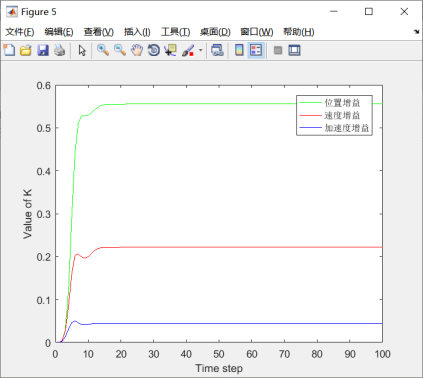
图5.5 滤波增益结果
(2)系统噪声改为都是均值为0的高斯噪声,均方差都是,观测噪声都是均值为0的高斯噪声,均方差都是30m,滤波均方误差初始值为单位阵的情况。
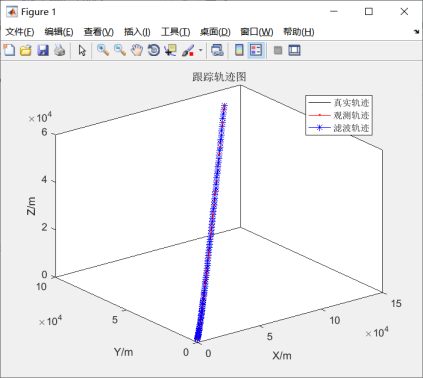
图5.6 卡尔曼滤波结果
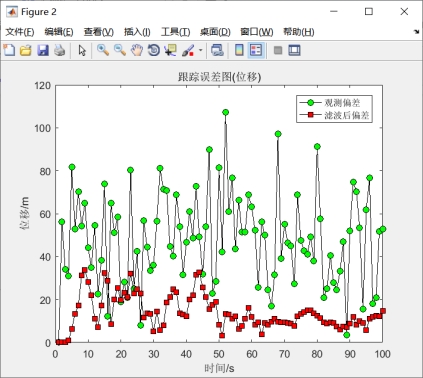
图5.7 位移跟踪误差结果
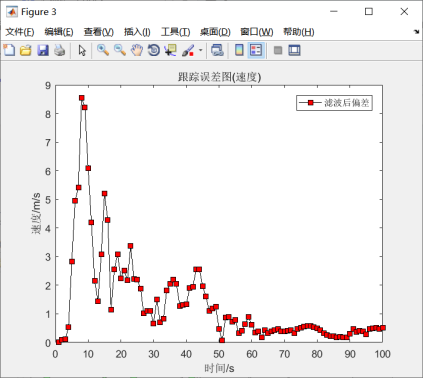
图5.8 速度跟踪误差结果
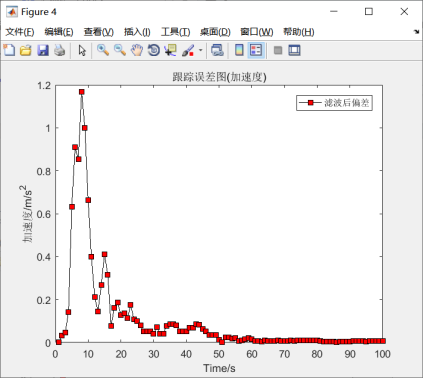
图5.9 加速度跟踪误差结果
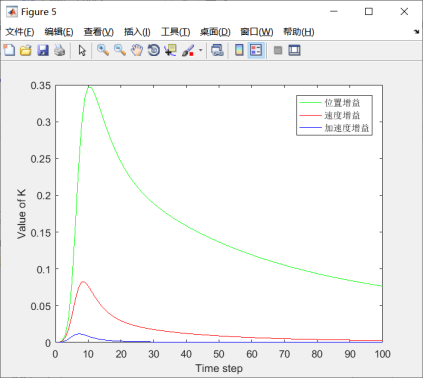
图5.10 滤波增益结果
仿真实验结果如图5.6-5.10所示。由图5.6可知,卡尔曼滤波依然能够很好的估计出目标的位置信息,对目标有较好的跟踪效果。由图5.7-5.9所示,滤波之后的位移偏差明显有所改善,速度和加速度,滤波增益都在趋于稳态。因此卡尔曼滤波是稳定的。说明模拟结果与事先假定的模型基本相符。
(3)系统噪声都是均值为0的高斯噪声,均方差都是,观测噪声都是均值为0的高斯噪声,均方差都是100m,滤波均方误差初始值为单位阵。
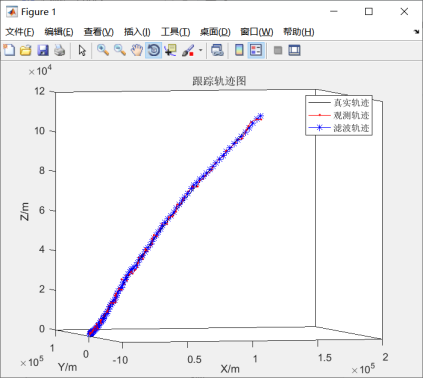
图5.11 跟踪轨迹图
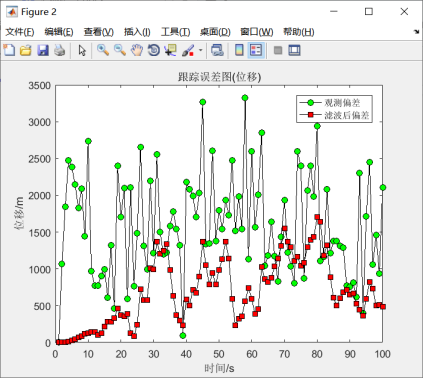
图5.12 位移跟踪误差图
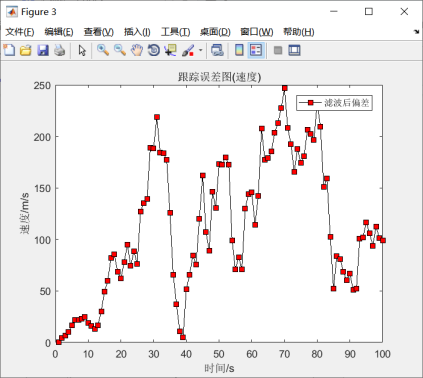
图5.13 速度跟踪误差图
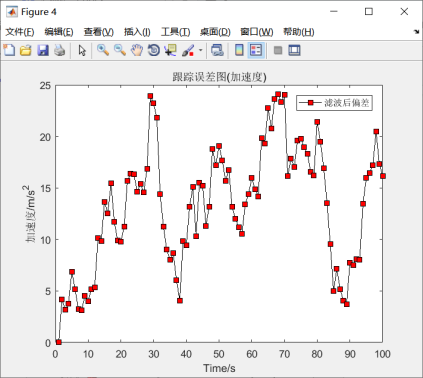
图5.14 加速度跟踪误差图
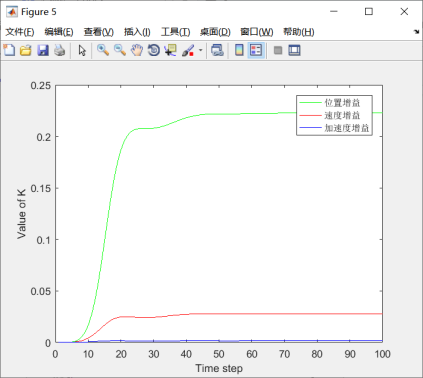
图5.15 滤波增益结果
仿真实验结果如图5.11-5.15所示。
由图5.11可知,观测轨迹出现更大的偏移,但是系统依然能够很好的预测出目标的位置信息。从图5.12-5.15来看,位移、速度、加速度都是在一定的区间上下浮动,总体来说,滤波之后的误差更小,同时增益也是很快趋于一个平稳值,说明卡尔曼滤波是稳定的。因此,系统模拟结果与先前假定的模型基本符合。
(4)系统噪声都是均值为0的高斯噪声,均方差都是,观测噪声都是均值为0的高斯噪声,均方差都是0.01m,滤波均方误差初始值为单位阵。
仿真实验结果如图5.16-5.20所示。
由图5.16可知,卡尔曼滤波对目标有较好的跟踪特性。从图5.17-5.19来看,尽管是在一定水平上下浮动的,但是从纵坐标数据来看,浮动数据之间减小,所以从宏观上来说,卡尔曼滤波是稳定的。因此系统模拟结果与先前假定的模型基本吻合。
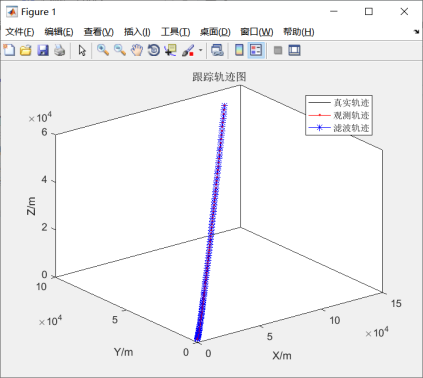
图5.16 跟踪轨迹图
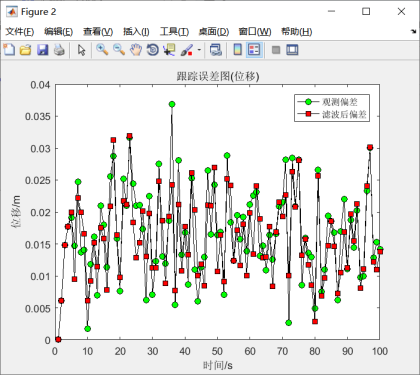
图5.17 位移跟踪误差图
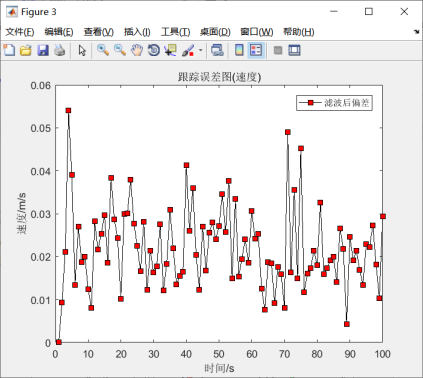
图5.18 速度跟踪误差图
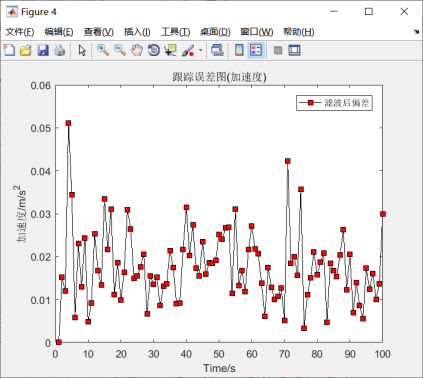
图5.19 加速度跟踪误差图
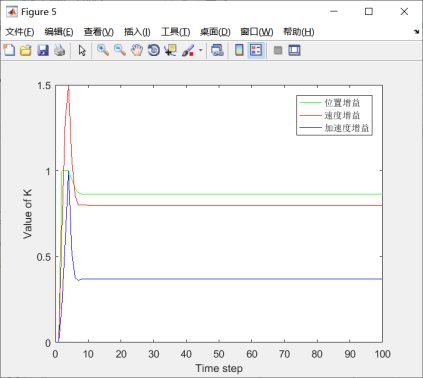
图5.20 增益效果图
由以上仿真结果可知,过程噪声和观测噪声的变化都能引起卡尔曼滤波误差的变化,当噪声减小时,误差减小,同时模型也能快速收敛;当噪声增大时,误差变大,同时模型收敛速度也变慢。此外还观察到加速度的变化对增益以及误差都会有所影响,主要原因是在模型中不管是位移还是速度,都受到自身加速度和噪声加速度的影响。
ps:以上内容均为我个人的观点和理解。如果在某些方面存在错误或不足,我非常欢迎各位读者提出宝贵的意见和建议,一同探讨和学习。
clc;
clear;
close all;
%% 设定初始数据以及初始化
n=9; % 状态维度
T=1; % 采样时间
N=100; % 跟踪总时长
% 过程噪声
q=0.01; % 过程噪声均方差
Qk=q^2*eye(3); % 定义过程噪声的协方差矩阵
% 观测噪声
p=30; % 观测噪声均方差
Pk=p^2*eye(3);
% 过程噪声和观测噪声都为高斯白噪声,均值为0,方差分别是Q和R
W=sqrtm(Qk)*randn(3,N); % 过程噪声:产生均值为0,方差为Q的一个(2*T)的随机数矩阵
V=sqrtm(Pk)*randn(3,N); % 观测噪声:高频随机干扰信号,产生均值为0,方差为Q的一个(2*T)的随机数矩阵
% 状态转移矩阵
A=[1, T, T^2/2';
0, 1, T ;
0, 0, 1 ];
Ak=blkdiag(A,A,A);
% 过程噪声驱动噪声
B=[ T^2/2;
T;
1 ];
Bk=blkdiag(B,B,B);
% 观测矩阵
H=[1,0,0,0,0,0,0,0,0;
0,0,0,1,0,0,0,0,0;
0,0,0,0,0,0,1,0,0];
X=zeros(9,N); % 定义一个矩阵存储信息
X(:,1)=[1000,200,20,1000,100,15,1000,100,10]'; % 定义初始状态向量,初始位置,初始速度,加速度
Z=zeros(3,N); % 雷达对位置的预测
Z(:,1)=[X(1,1),X(4,1),X(7,1)]; % 观测值初始化 %[1000,1000,1000]
Xkf=zeros(9,N); %Kalman滤波初始化
Xkf(:,1)=X(:,1);
K_store = zeros(9, 3, N); % 初始化一个用于存储增益K的三维矩阵
P=eye(9); % 协方差阵初始化
%% 模拟目标运动,观测站对目标进行观测,卡尔曼滤波,生成真实轨迹,观测轨迹和滤波轨迹
for k=2:N
% 目标真实轨迹
X(:,k)=Ak*X(:,k-1)+Bk*W(:,k-1); % 系统状态方程
% 目标观测轨迹
Z(:,k)=H*X(:,k)+V(:,k); % 系统的观测方程
% 开始滤波
Xpred=Ak*Xkf(:,k-1); % 第一步:状态预测
Ppred=Ak*P*Ak'+Bk*Qk*Bk'; % 第二步:协方差预测
K=Ppred*H'*inv(H*Ppred*H'+Pk); % 第三步:求增益 %inv:矩阵求逆
K_store(:,:,k) = K; % 保存增益K的值
Xkf(:,k)=Xpred+K*(Z(:,k)-H*Xpred); % 第四步:状态更新
P=(eye(9)-K*H)*Ppred; % 第五步:协方差更新
end
%% 绘制轨迹图
figure
hold on;
box on;
title('跟踪轨迹图');
xlabel('X/m');
ylabel('Y/m');
zlabel('Z/m');
plot3(X(1,:),X(4,:),X(7,:),'-k'); % 真实轨迹
plot3(Z(1,:),Z(2,:),Z(3,:),'-r.'); % 观测轨迹
plot3(Xkf(1,:),Xkf(4,:),Xkf(7,:),'-b*'); % Kalman滤波轨迹
legend('真实轨迹','观测轨迹','滤波轨迹')
view(3); % 设置三维视角
%% 位移误差分析
for i=1:N
Err_Observation(i)=RMS(X(:,i),Z(:,i)); % 滤波前误差
Err_KalmanFilter(i)=RMS(X(:,i),Xkf(:,i)); % 滤波后误差
end
% 画图
figure
hold on;
box on;
title('跟踪误差图(位移)');
xlabel('时间/s');
ylabel('位移/m');
plot(Err_Observation,'-ko','MarkerFace','g');
plot(Err_KalmanFilter,'-ks','MarkerFace','r');
legend('观测偏差','滤波后偏差')
%% 速度误差分析
for i=1:N
Err_KalmanFilter(i)=RMS1(X(:,i),Xkf(:,i)); % 滤波后误差
end
% 画图
figure
hold on;
box on;
title('跟踪误差图(速度)');
xlabel('时间/s');
ylabel('速度/m/s');
plot(Err_KalmanFilter,'-ks','MarkerFace','r');
legend('滤波后偏差')
%% 加速度误差分析
for i=1:N
Err_KalmanFilter(i)=RMS2(X(:,i),Xkf(:,i)); % 滤波后误差
end
% 画图
figure
hold on;
box on;
title('跟踪误差图(加速度)');
xlabel('Time/s');
ylabel('加速度/m/s^2');
plot(Err_KalmanFilter,'-ks','MarkerFace','r');
legend('滤波后偏差')
%%
figure
title('增益K随时间的变化');
plot(squeeze(K_store(1,1,:)), 'g'); % 位置对应的增益随时间的变化
hold on; % 绘制多条曲线命令
plot(squeeze(K_store(2,1,:)), 'r'); % 速度对应的增益,用红色表示
hold on;
plot(squeeze(K_store(3,1,:)), 'b'); % 加速度对应的增益,用蓝色表示
xlabel('Time step');
ylabel('Value of K');
legend('位置增益','速度增益','加速度增益')
%% 计算位移欧氏距离
function deviation=RMS(X1,X2)
if length(X2)<=3
deviation=sqrt((X1(1)-X2(1))^2+(X1(4)-X2(2))^2+(X1(7)-X2(3))^2); % 返回X1和X2之间的欧式距离
else
deviation=sqrt((X1(1)-X2(1))^2+(X1(4)-X2(4))^2+(X1(7)-X2(7))^2); %
end
end
%% 计算速度误差
function deviation1 = RMS1(X1,X2)
deviation1=sqrt((X1(2)-X2(2))^2+(X1(5)-X2(5))^2+(X1(8)-X2(8))^2); % 返回X1和X2之间的欧式距离
end
%% 计算加速度误差
function deviation1 = RMS2(X1,X2)
deviation1=sqrt((X1(3)-X2(3))^2+(X1(6)-X2(6))^2+(X1(9)-X2(9))^2); % 返回X1和X2之间的欧式距离
end参考资料与文献
- 基于卡尔曼滤波算法在三维球轨迹中跟踪应用-CSDN博客
- 机动目标跟踪——匀加速运动模型(一维)_目标跟踪运动模型-CSDN博客
- 黄小平,王岩.卡尔曼滤波原理及应用[M].电子工业出版社,2015.
结语: 恭喜你完成了这篇博客的阅读!我衷心希望我的分享能够为你带来启发和帮助。愿你拥有一个宁静而美好的夜晚,好梦相伴。🌛🌛🌛























 1190
1190

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








