高等数学 映射

1.映射的概念

什么叫映射，在书中我们定义为两个非空集合X，Y，存在一个法则使得对X中的每个元素x都能按照法则在Y中找到唯一对应值，这就叫映射。

然而书中讲的比较晦涩难懂，下面我将通过图来加深大家对概念的理解：

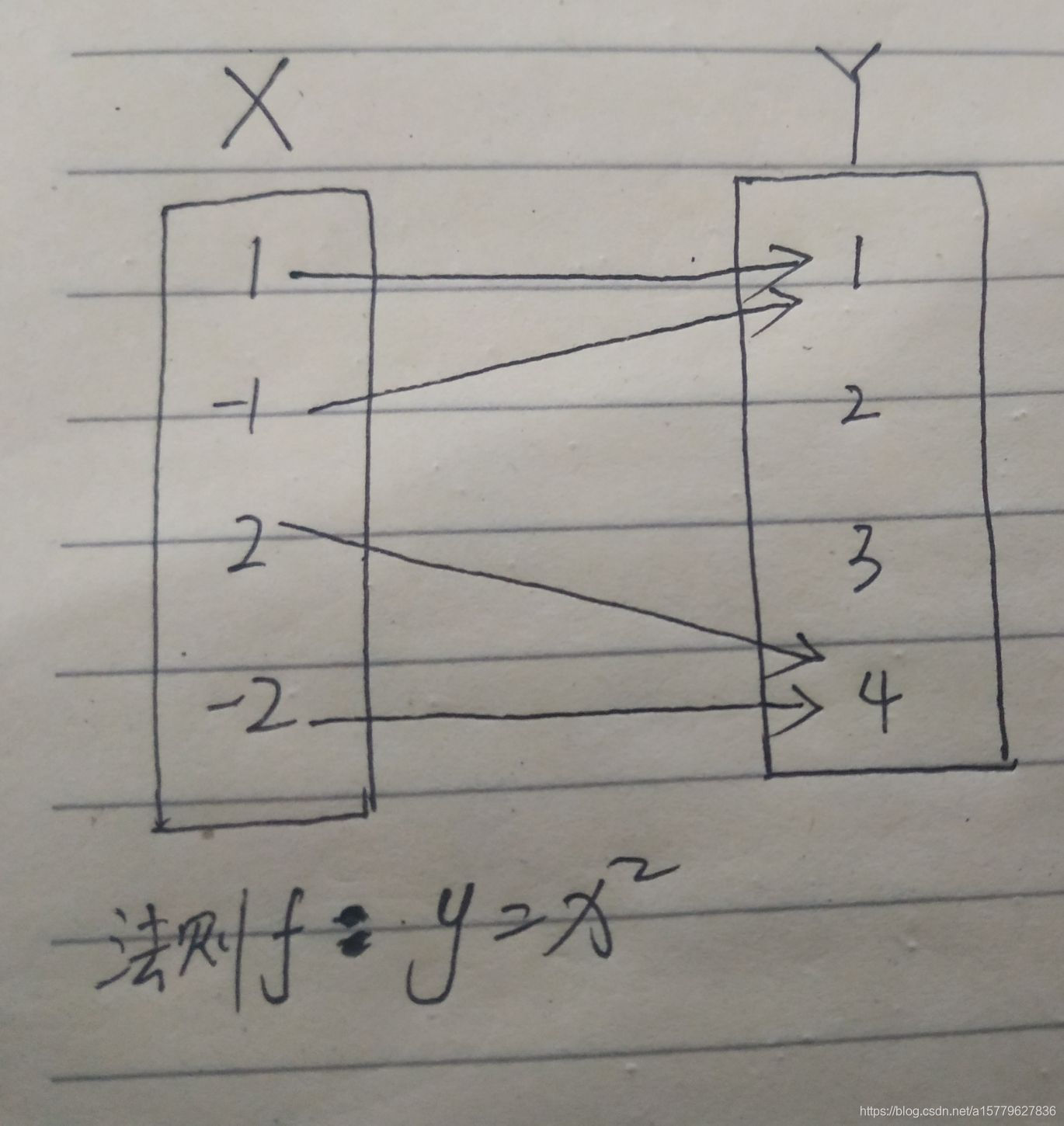
如上图：根据这个定义，我们可以从中得知，x与y的关系，是多对一的关系，也就是说允许大于等于一个x对应同一个y，但是每个x只能指向一个y，这听起来有点拗口，但是请记住“x与y的关系是多对一的”，这里的多是指大于等于一。

在这里，我们称x为元素y的一个原像，而y称为元素x的像。

而根据定义我们可以知道，在映射关系中，X中的每个元素x都能在Y中找到唯一对应的元素y，根据这个我们可以得出：

X中的所有元素都必须能在Y中找到对应的像，而Y中的元素则不一定能在X中找到原像。也就是书上所说的对于对应法则f，f（x）的值域与Y是被包含关系。

如果当Y中的元素都能在X中找到原像，那我们就称这个映射为：满射。

当在映射中X与Y的关系，也就是像与原像的关系是一一对应时，我们就称之为：单射

当这个映射满足单射和，满射两个关系时，我们就称之为：双射

 

2.逆映射与复合映射 

逆映射在书中是这样说到：只有在单射才存在逆映射。但是从映射的定义看来：两个非空集合X，Y，存在一个法则使得对X中的每个元素x都能按照法则在Y中找到唯一对应值。 注意，书中说的是X中的每个元素x都能在Y中找到像。

所以满足单射是逆映射的一个充分条件，而非充要条件，既是逆映射，则就是X与Y能颠倒运算，也就是X和Y既能做原像，也能做像，所以一个逆运算必须满足满射和单射的条件，也就是双射。

也就是说双射是逆运算的充要条件。

 

对于复合映射如下图所示：

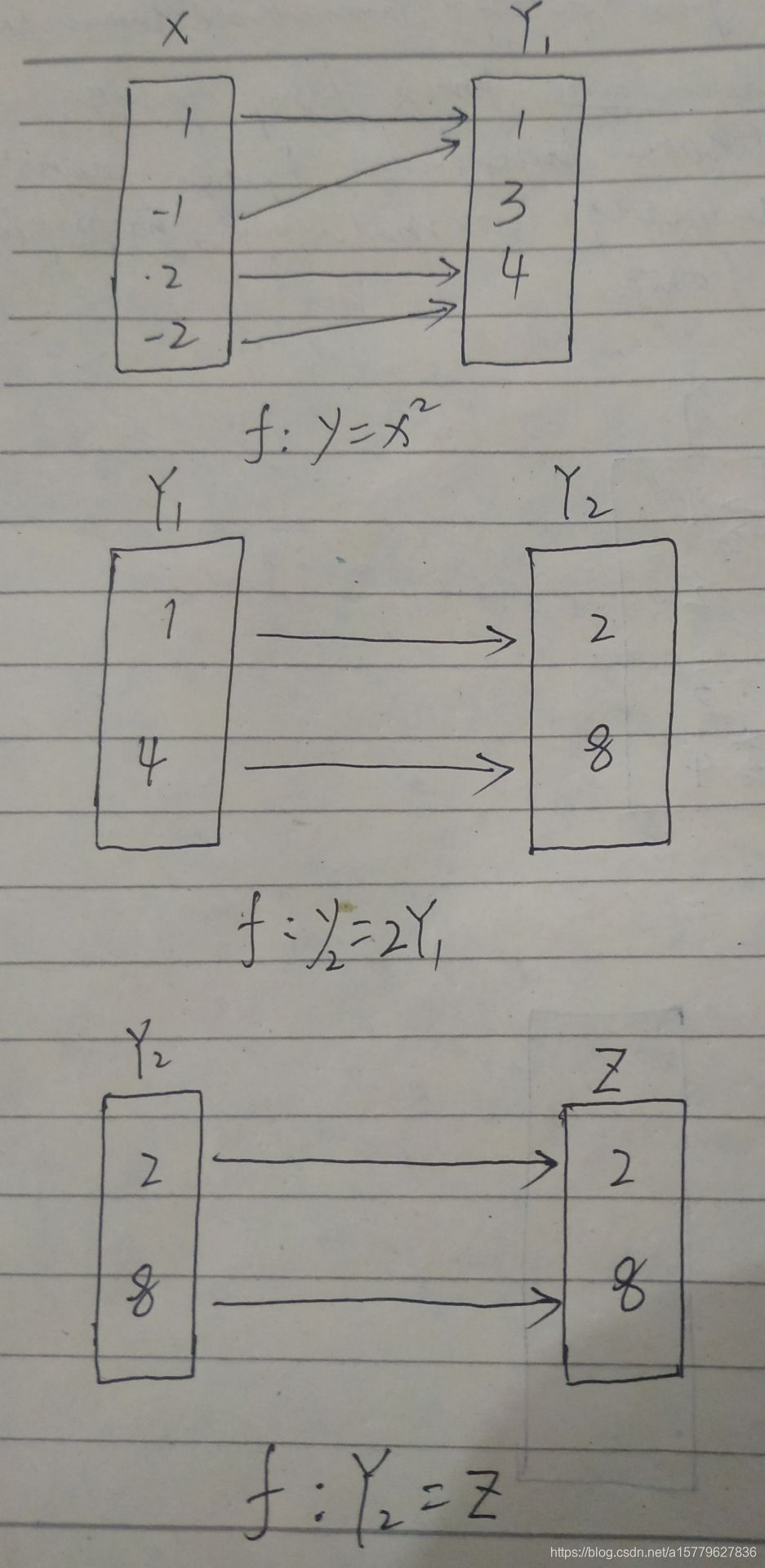
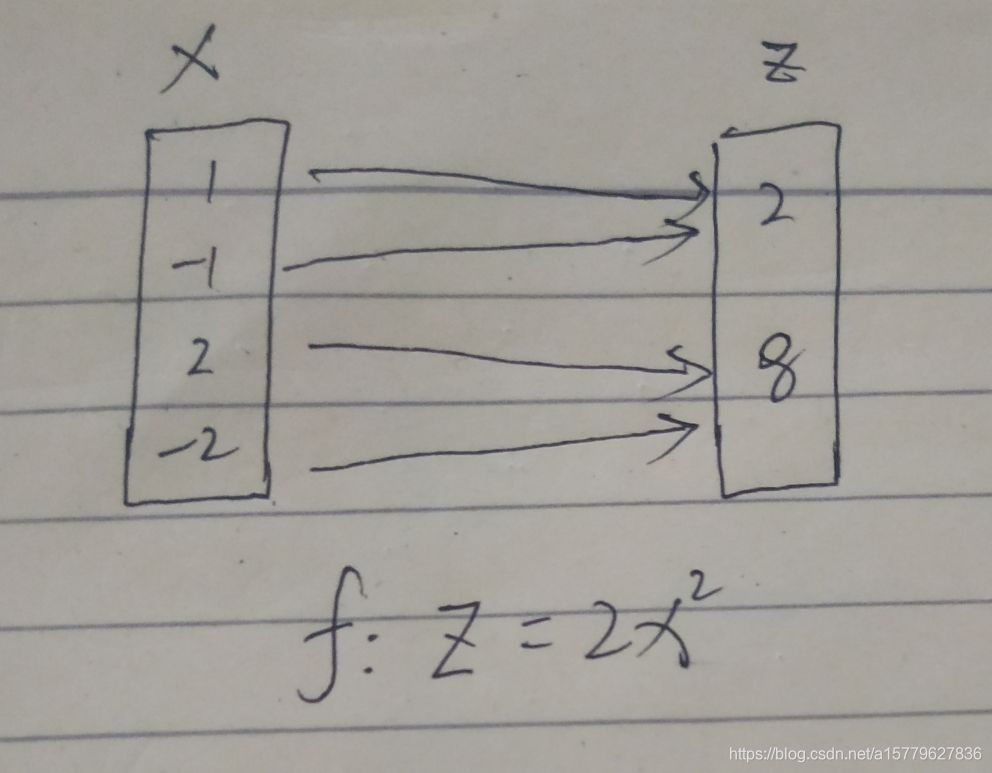
 如上两图所示，对于复合映射，我们可以理解为一个复合运算，其实和复合运算类似。就是对于两个“g：X—Y1，f：Y2—Z”映射而言，X—Y1映射的像也就是Y1能找到一个对应法则并使Y1中有原像的元素y在Y2中找到像，我们就称“g和f构成复合映射”

由定义可知g的值域必须包含在Y2的定义域内，否则不能构成复合映射。

其次，映射是有顺序的g与f的复合映射有意义不代表f与g的复合映射有意义，即使他们都有意义，但其意义未必相同。

具体详情，可以自己画图理解。