《概率论与数理统计》学习笔记3-二维随机变量及其分布

目录

二维随机变量及其分布函数

二维离散型随机变量及其概率分布

连续型随机变量及其概率密度

条件分布

二维随机变量的函数分布

---

二维随机变量及其分布函数

        二维随机变量的定义：

                X和Y是定义在随机试验E的样本空间Ω上的两个随机变量，他们构成的向量（𝑋，𝑌）称为二维随机变量/向量

        二维随机变量分布函数的定义：

                {𝑋≤𝑥}与{𝑌≤𝑦}的交事件记为{𝑋≤𝑥,𝑌≤𝑦}，则称：

                为二维随机变量（𝑋，𝑌）的分布函数/联合分布函数

        二维随机变量分布函数𝐹(𝑥,𝑦)的性质：

                1）

                        对任意固定x：

                2）𝐹(𝑥,𝑦)对每个固定变量是单调不减函数

                3）𝐹(𝑥,𝑦)关于x和y均右连续

                4）对任意的𝑥1<𝑥2，𝑦1<𝑦2，有：

        边缘分布：

                随机变量X的分布函数为𝐹𝑋(𝑥)，随机变量Y的分布函数为𝐹𝑌(𝑦)，分别称为二维随机变量（𝑋，𝑌）的关于X和关于Y的边缘分布函数

        随机变量的独立性：

                二维随机变量（𝑋，𝑌）与边缘分布函数𝐹𝑋(𝑥)和𝐹𝑌(𝑦)满足:

                则称X与Y相互独立

二维离散型随机变量及其概率分布

        二维离散型随机变量的定义：

                如果二维随机变量（𝑋，𝑌）所有可能取值是有限对或可列无限对，则称（𝑋，𝑌）是二维离散型随机变量

        二维离散型随机变量的概率分布/联合分布律：

                上式称为二维随机变量（𝑋，𝑌）的概率分布或联合分布律

        边缘概率分布/边缘分布律：

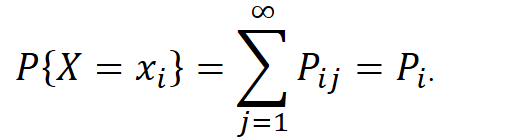
                上式称为二维随机变量（𝑋，𝑌）关于X的边缘分布律

        离散型随机变量的独立性：

                上式为离散型随机变量X和Y相互独立的充分必要条件

连续型随机变量及其概率密度

        二维连续型随机变量及概率密度的定义：

                 称(𝑋,𝑌)为二维连续型随机变量，𝐹(𝑥,𝑦)为分布函数，𝑓(𝑥,𝑦)为联合概率密度

        概率密度𝑓(𝑥,𝑦)的性质：

                1）𝑓(𝑥,𝑦)≥0

                2）

                3）若𝑓(𝑥,𝑦)在(𝑥,𝑦)处连续：

                4）

        边缘概率密度：

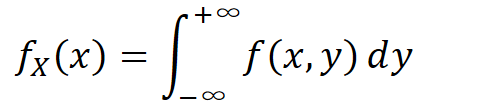
                𝑓𝑋(𝑥)称为二维随机变量𝑋,𝑌关于X的边缘概率密度

        连续型随机变量的独立性：

                上式为连续型随机变量X和Y相互独立的充分必要条件

        二维均匀分布：

                称（X，Y）在区域D上服从均匀分布

        二维正态分布：

                称（X，Y）服从参数为(𝜇1，𝜇2，𝜎1，𝜎2，𝜌)的二维正态分布，记作:

                X和Y相互独立的充分必要条件是𝜌=0

条件分布

        离散型随机变量的条件分布：

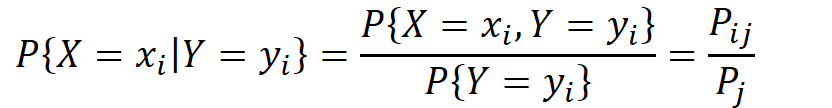
                为在条件𝑌=𝑌𝑗下随机变量X的条件概率分布

        连续型随机变量的条件分布：

                若极限存在，则称此极限值𝐹𝑋|𝑌(𝑋|𝑌)为在Y=y的条件下X的条件分布函数

                𝑓𝑋|𝑌(𝑥|𝑦)称为在Y=y的条件下X的条件概率密度

二维随机变量的函数分布

        二维离散型随机变量的函数分布：

                列出𝑋+𝑌、𝑋/𝑌所有可能取值，计算二维变量中所有符合条件的概率之和

        二维连续型随机变量的函数分布：

                Z的函数分布为：

                其概率密度为：

        X+Y的概率密度密度：

                如果X和Y相互独立：

                若X和Y服从正态分布𝑋~𝑁(𝜇1,𝜎12)和𝑌~𝑁(𝜇2,𝜎22)，则Z=X+Y也服从正态分布，且:

        𝑀=𝑚𝑎𝑥(𝑥,𝑦)和𝑁=𝑚𝑖𝑛(𝑥,𝑦)的分布函数：