四元数：从复数到四元数

0、前言

所谓四元数（Quaternion），一句话说就是复数的拓展，那么四元数只是简单的维度增加的复数吗？它代表了什么样的物理意义和数学道理呢？

1、四元数的定义

四元数是复数的拓展。我们知道一个复数是：

如果我们将复数的实部和虚部同样表示成复数，且这两个新的复数采用新的复数单位，即：

再规定新加上新的复数单位后的复数单位之间的运算：

那么新的表示为：

那么这个由三个复数单位表示的“超复数 (Hyper-complex)”，就叫做四元数，用Q表示，我们整理一下表示方法，也可写作：

值得一提的是，如果我们继续将四元数的实部和虚部的所有指数写成复数并加入更多的复数单位，我们可以得到7个复数单位的八维复数，称为八元数(Octonion)或双四元数(Bi-quaternion)。以此类推还有16元数、32元数等等。

2、四元数的运算法则

2.1 四元数的复数单位：

四元数的三个复数单位的运算法则如下：

2.2 四元数的模值：

2.3 四元数乘法：

3、四元数的物理意义 

3.1 旋转的自由度

我们知道，我们如果把复数看成一个二维矢量，对复数乘上一个复数，就相当于对其进行旋转和拉伸，而乘以单位复数相当于二维旋转。

复数有两个自由度，就是它的实部和虚部，如果用极坐标表示：

那么它的自由度就是它的模长（1个自由度）和旋转（1个自由度）。

所以复数乘法，相当于对二维空间的向量进行旋转+拉伸。

而四元数也是相同的道理。

先给出结论，四元数乘法，相当于对三维空间的向量进行旋转+拉伸。

上面说到，不管模长，复数旋转是一个自由度。

那么我们看四元数，毫无疑问它的自由度是4，减去模长的一个自由度，那么可知四元数的旋转是三个自由度。

那如何理解四元数的旋转（三维旋转）是三个自由度?

3.2 复数旋转/二维旋转

还是先从复数说起。其实旋转存在一个旋转轴，假设旋转前的向量为，旋转后的向量为，旋转轴为，垂直于和同在的平面，向量绕旋转轴旋转。

二维空间中， 对于任意的和，它们同在的平面始终是xy平面，因此所有二维旋转的旋转轴都是相同的，都是垂直于xy平面的，唯一的自由度就是旋转的角度。

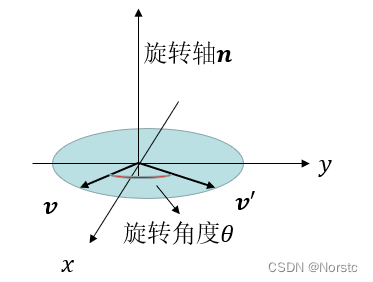
3.3 四元数旋转/三维旋转

三维空间中，对于任意的  和 ，它们同在的平面不一定相同，因此旋转的旋转轴是在变化的。

所以为了描述三维旋转，在确定旋转角度的同时，也要确定旋转轴。

三维空间的旋转轴，也就是三维向量的方向，其自由度为2，所以有：

旋转轴自由度+旋转角度自由度=2+1=3，这与我们先前的结论相同。

实际上，四元数也可以用极坐标的形式表示，即：

 具体推导涉及四元数的欧拉公式，这里不赘述。

下图给出了三维旋转的示例，其中h和h'是旋转前和旋转后的向量，ψ是旋转角度。