零、前言
对于条件分布(y|x;θ),对于线性回归模型有![]() ,而对分类问题有
,而对分类问题有![]() 。其实这些分布均是广义线性模型(GLM)的特殊情况。
。其实这些分布均是广义线性模型(GLM)的特殊情况。
我们通过定义广义线性模型,可以据此求出拟合函数h(x)
一、指数分布族(Exponential Family)
其定义如下
![]()
其中,η称为自然参数(natural parameter),T(y)称为充分统计量(sufficient statistic)(通常T(y)=y)。当a、b、T都确定了,就定义了以η为参数的指数分布族。
下面以伯努利分布与正态分布为例子,从指数分布族推导出它们。
1.1 Bernoulli分布
伯努利分布可写作:

对比指数分布族的定义,可知![]() ,同时也有:
,同时也有:

注意,这时我们可以得到![]() ,即sigmoid函数的表达式,其意义后篇将说明。
,即sigmoid函数的表达式,其意义后篇将说明。
1.2 Gaussian分布
实际上,σ^2的选取不影响各函数与参数的确定,这里不再证明,为了简化,我们令σ^2=1,于是有

根据指数分布族的定义,我们得到

实际上,指数分布、泊松分布、伽马分布、狄利赫里分布等很多分布也属于指数分布族,这里不再叙述。
二、GLM模型的建立
2.0 GLM的假设
对于回归或是分类问题,我们的目标是若其分布属于指数分布族的某种分布,那么根据这求出拟合函数h。具体假设如下:
1.![]()
2.拟合函数h为条件概率期望关于特征x的函数,即![]()
3.自然参数满足![]()
其中假设3对η的线性假设,就是GLM中线性的由来。
2.1 普通的最小二乘
在线性回归模型中,最小二乘是最大似然,其中y|x服从高斯分布。
那么在GLM,若假设对给定x的y服从高斯分布,根据前文的证明,有μ=η,又根据线性假设η=θTx,所以μ=θTx=E(y|x)=h(x),所以得到h是线性回归
2.2 Logistic回归
对于二分问题,根据前文所述,有![]() ,根据线性假设,有φ
,根据线性假设,有φ![]() =hθ(x),所以在二分问题中,h为logistic回归/sigmoid分布
=hθ(x),所以在二分问题中,h为logistic回归/sigmoid分布
2.3 Softmax回归
由二分问题演化,现在考虑k分问题,即y是离散的且。
分类问题要对每个类别有一个判决概率φi。注意到如果对与k个分类都有对应的概率的话,会出现冗余。因为如果知道k-1个概率的话,第k个可以从其补集求出。因此,我们定义k-1个概率,![]() ,且有
,且有![]() ,那么有
,那么有![]() ,因此令
,因此令![]() 。
。
我们队T(y)的定义如下

为一k-1维向量。
那么多项式分布可表示如下
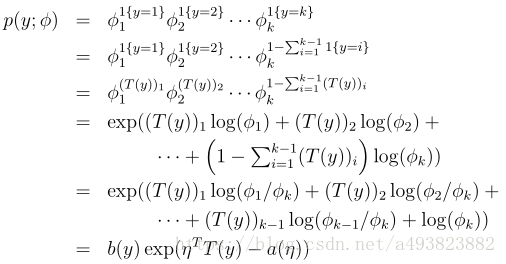
所以多项式分布也属于指数分布族,且有

令![]() ,那么有
,那么有

所以得到![]() ,将其带入到φi中有
,将其带入到φi中有

上式将η映射到φi,此函数称为softmax函数
又根据线性假设,对于每个η有![]() ,同时令ηk=0,对求和式没有影响,那么有
,同时令ηk=0,对求和式没有影响,那么有

综上所述,得到的预测函数h为:
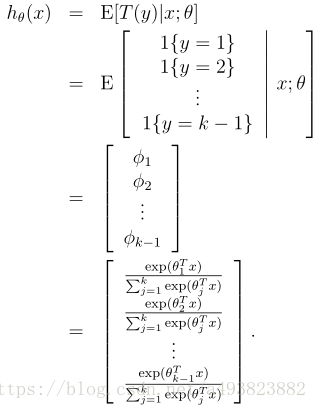
这是对于前k-1个概率,那么φk可用补集的方法求出。
最后是对softmax回归的参数最优化,对其输入m个训练样本的对数似然函数易得如下

对此最大化可用牛顿法或梯度上升法等
























 2588
2588

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








