【集成学习】task2 回归模型

使用sklearn构建完整机器学习项目流程

• 明确项目任务：回归/分类
• 收集数据集并选择合适的特征。
• 选择度量模型性能的指标。
• 选择具体的模型并进行训练以优化模型。
• 评估模型的性能并调参。

回归模型

回归分析是一种预测性的建模技术，它研究的是因变量（目标）和自变量（特征）之间的关系。这种技术通常用于预测分析，时间序列模型以及发现变量之间的因果关系。通常使用曲线/线来拟合数据点，目标是使曲线到数据点的距离差异最小。

本节依旧以波斯顿房价数据集为例

# 引入相关科学计算包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline 
plt.style.use("ggplot")      
import seaborn as sns

from sklearn import datasets
boston = datasets.load_boston()     # 返回一个类似于字典的类
X = boston.data
y = boston.target
features = boston.feature_names
boston_data = pd.DataFrame(X,columns=features)
boston_data["Price"] = y
boston_data.head()

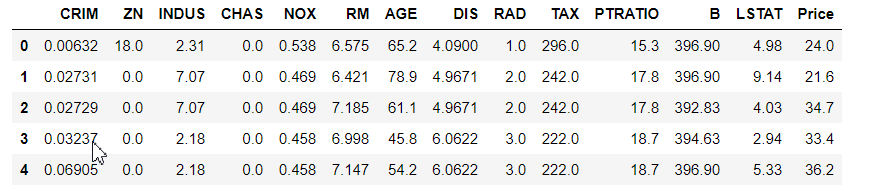
特征含义

• CRIM：各城镇的人均犯罪率
• ZN：规划地段超过25,000平方英尺的住宅用地比例
• INDUS：城镇非零售商业用地比例
• CHAS：是否在查尔斯河边(=1是)
• NOX：一氧化氮浓度(/千万分之一)
• RM：每个住宅的平均房间数
• AGE：1940年以前建造的自住房屋的比例
• DIS：到波士顿五个就业中心的加权距离
• RAD：放射状公路的可达性指数
• TAX：全部价值的房产税率(每1万美元)
• PTRATIO：按城镇分配的学生与教师比例
• B：1000(Bk - 0.63)^2其中Bk是每个城镇的黑人比例
• LSTAT：较低地位人口
• Price：房价

回归模型评价指标

• MSE均方误差：$\text{MSE}(y,\hat{y})=\frac{1}{n_{\text{samples}}}{\sum }_{i=0}^{n_{\text{samples}}-1}(y_i-{\hat{y}}_i{)}^2.$
• MAE平均绝对误差:$\text{MAE}(y,\hat{y})=\frac{1}{n_{\text{samples}}}{\sum }_{i=0}^{n_{\text{samples}}-1}\left|y_i-{\hat{y}}_i\right|$
• $R^2$决定系数：$R^2(y,\hat{y})=1-\frac{{\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2}{{\sum }_{i=1}^n(y_i-\bar{y}{)}^2}$
• 解释方差得分: e x p l a i n e d _ v a r i a n c e ( y , y ^ ) = 1 − V a r { y − y ^ } V a r { y } explained\_{}variance(y, \hat{y}) = 1 - \frac{Var\{ y - \hat{y}\}}{Var\{y\}} explained_variance(y,y^​)=1−Var{y}Var{y−y^​}​

https://scikit-learn.org/stable/modules/model_evaluation.html#regression-metrics

在这个案例中，我们使用MSE均方误差为模型的性能度量指标。

---

线性回归模型

线性回归就是回归问题中的一种，线性回归假设目标值与特征之间线性相关，即满足一个多元一次方程。通过构建损失函数，来求解损失函数最小时的参数w ：
假设：数据集 D = { ( x 1 , y 1 ) , . . . , ( x N , y N ) } D = \{(x_1,y_1),...,(x_N,y_N) \} D={(x1​,y1​),...,(xN​,yN​)}，$x_i\in R^p,y_i\in R,i=1,2,...,N$，$X=(x_1,x_2,...,x_N{)}^T,Y=(y_1,y_2,...,y_N{)}^T$
假设X和Y之间存在线性关系，模型的具体形式为$\hat{y}=f(w)=w^{T}x$

(a) 最小二乘估计：
我们需要衡量真实值$y_i$与线性回归模型的预测值$w^T{x}_i$之间的差距，在这里我们和使用二范数的平方和L(w)来描述这种差距，即：
$$\begin{gathered} L(w)=\sum _{i=1}^N||w^T{x}_i-y_i|{|}_2^2=\sum _{i=1}^N(w^T{x}_i-y_i{)}^2=(w^T{X}^T-Y^T)(w^T{X}^T-Y^T{)}^T=w^T{X}^{T}Xw-2w^T{X}^{T}Y+Y{Y}^T \\ 因此，我们需要找到使得L(w)最小时对应的参数w，即： \\ \hat{w}=argminL(w) \\ 为了达到求解最小化L(w)问题，我们应用高等数学的知识，使用求导来解决这个问题： \\ \frac{\partial L(w)}{\partial w}=2X^{T}Xw-2X^{T}Y=0,因此： \\ \hat{w}=(X^{T}X{)}^{-1}{X}^{T}Y \end{gathered}$$
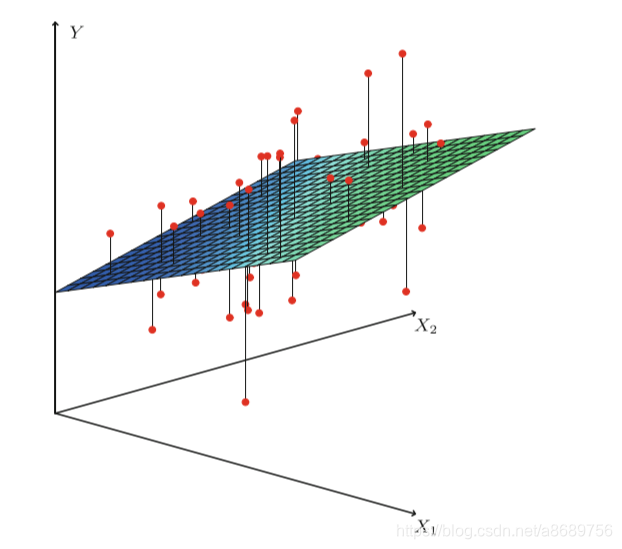
(b) 几何解释：
在线性代数中，我们知道两个向量a和b相互垂直可以得出：$<a,b>=a.b=a^{T}b=0$,而平面X的法向量为Y-Xw，与平面X互相垂直，因此：$X^T(Y-Xw)=0$，即：$w=(X^{T}X{)}^{-1}{X}^{T}Y$

© 概率视角：
假设噪声$ϵ\backsim N(0,{\sigma }^2),y=f(w)+ϵ=w^{T}x+ϵ$，因此：$y|x_i,wN(w^{T}x,{\sigma }^2)$
我们使用极大似然估计MLE对参数w进行估计：
$$\begin{gathered} L(w)=logP(Y|X;w)=log\prod _{i=1}^{N}P(y_i|x_i;w)=\sum _{i=1}^{N}logP(y_i|x_i;w) \\ =\sum _{i=1}^{N}log(\frac{1}{\sqrt{2\pi \sigma }}exp(-\frac{(y_i-w^T{x}_i{)}^2}{2{\sigma }^2}))=\sum _{i=1}^N[log(\frac{1}{\sqrt{2\pi }\sigma })-\frac{1}{2{\sigma }^2}(y_i-w^T{x}_i{)}^2] \\ argma{x}_{w}L(w)=argmi{n}_w[l(w)=\sum _{i=1}^N(y_i-w^T{x}_i{)}^2] \\ 因此：线性回归的最小二乘估计<==>噪声ϵ\backsim N(0,{\sigma }^2)的极大似然估计 \end{gathered}$$

使用线性回归演示

from sklearn import linear_model      # 引入线性回归方法
lin_reg = linear_model.LinearRegression()       # 创建线性回归的类
lin_reg.fit(X,y)        # 输入特征X和因变量y进行训练
print("模型系数：",lin_reg.coef_)             # 输出模型的系数
print("模型得分：",lin_reg.score(X,y))    # 输出模型的决定系数R^2

线性回归的推广

在线性回归中，我们假设因变量和特征之间是线性关系，但是当数据存在非线性关系时就无法用线性回归去表达，我们想去推广线性回归模型，使得推广后的模型更能表达非线性的关系，可以采用以下方法：

其他方法见：非线性模型：多项式回归、局部样条、平滑样条、 广义相加模型GAM分析https://www.bilibili.com/read/cv10113813

多项式回归

为了体现因变量和特征的非线性关系，一个很自然而然的想法就是将标准的线性回归模型：
$$y_i=w_0+w_1{x}_i+{ϵ}_i$$
换成一个多项式函数：
$$y_i=w_0+w_1{x}_i+w_2{x}_i^2+...+w_d{x}_i^d+ϵ$$
对于多项式的阶数d不能取过大，一般不大于3或者4，因为d越大，多项式曲线就会越光滑，在X的边界处有异常的波动。
多项式回归实例介绍：
https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.PolynomialFeatures.html?highlight=poly#sklearn.preprocessing.PolynomialFeatures
sklearn.preprocessing.PolynomialFeatures(degree=2, *, interaction_only=False, include_bias=True, order=‘C’):

• 参数：

degree：特征转换的阶数。
interaction_onlyboolean：是否只包含交互项，默认False 。
include_bias：是否包含截距项，默认True。 order：str in {‘C’, ‘F’},
default ‘C’，输出数组的顺序。

from sklearn.preprocessing import PolynomialFeatures
X_arr=np.arange(6).reshape(3,2)
print('原始X为：\n',X_arr)


#生成一个新的特征矩阵，该矩阵由度小于或等于指定度的特征的所有多项式组合组成。例如，如果输入样本是二维且格式为[a，b]，
#则2阶多项式特征为[1，a，b，a ^ 2，ab，b ^ 2]。
poly = PolynomialFeatures(2)
print("2次转化X：\n",poly.fit_transform(X_arr))


#只包含交互项,即1,a,b,ab
poly=PolynomialFeatures(interaction_only=True) 
print("2次转化X：\n",poly.fit_transform(X_arr))

---

广义可加模型(GAM)：

广义可加模型GAM实际上是线性模型推广至非线性模型的一个框架，在这个框架中，每一个变量都用一个非线性函数来代替，但是模型本身保持整体可加性。GAM模型不仅仅可以用在线性回归的推广，还可以将线性分类模型进行推广。具体的推广形式是：
标准的线性回归模型：
$$y_i=w_0+w_1{x}_{i1}+...+w_p{x}_{ip}+{ϵ}_i$$
GAM模型框架：
$$y_i=w_0+\sum _{j=1}^p{f}_j(x_{ij})+{ϵ}_i$$
GAM模型的优点与不足：

• 优点：

简单容易操作，能够很自然地推广线性回归模型至非线性模型，使得模型的预测精度有所上升；
由于模型本身是可加的，因此GAM还是能像线性回归模型一样把其他因素控制不变的情况下单独对某个变量进行推断，极大地保留了线性回归的易于推断的性质。

• 缺点：

GAM模型会经常忽略一些有意义的交互作用，比如某两个特征共同影响因变量，不过GAM还是能像线性回归一样加入交互项$x^{(i)}\times x^{(j)}$的形式进行建模；
但是GAM模型本质上还是一个可加模型，如果我们能摆脱可加性模型形式，可能还会提升模型预测精度