2022考研笔记-数学(python实现-极坐标系下的各种图形)

1.极坐标系下的各种图形

笛卡尔心形线为极坐标系下的数学常见图形
本案例用numpy和matplotlib库实现

• NumPy(Numerical Python) 是 Python
  语言的一个扩展程序库，支持大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库。
• Matplotlib 是 Python 编程语言及其数值数学扩展包 NumPy 的可视化操作界面。它为利用通用的图形用户界面工具包，如
  Tkinter, wxPython, Qt 或 GTK+ 向应用程序嵌入式绘图提供了应用程序接口（API）。

import numpy as np 
import matplotlib.pyplot as plt

# 心形线
a = 1
theta = np.linspace(0, 2*np.pi, 1000)
r = a*(1 - np.cos(theta))
plt.axes(polar = True)
plt.plot(theta, r)
plt.show()

# 玫瑰线
a = 1
theta = np.linspace(0, 2*np.pi, 1000)
r = a* np.sin(3*theta)
plt.axes(polar = True)
plt.plot(theta, r)
plt.show()

# 阿基米德螺线
a = 1
theta = np.linspace(0, 10*np.pi, 1000)
r = a * theta
plt.axes(polar = True)
plt.plot(theta, r)
plt.show()

# 伯努利双纽线
a = 1
theta = np.linspace(0, 2*np.pi, 1000)
r = np.sqrt(2*(a**2)*np.cos(2*theta))
plt.axes(polar = True)
plt.plot(theta, r)
plt.show()

画出四个图形如下：

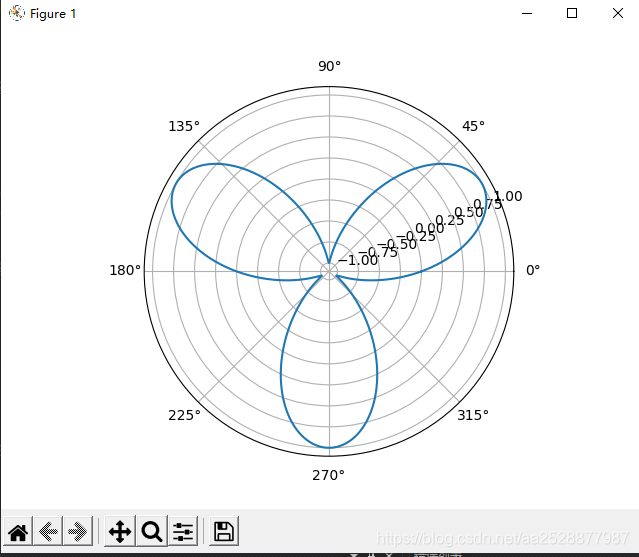
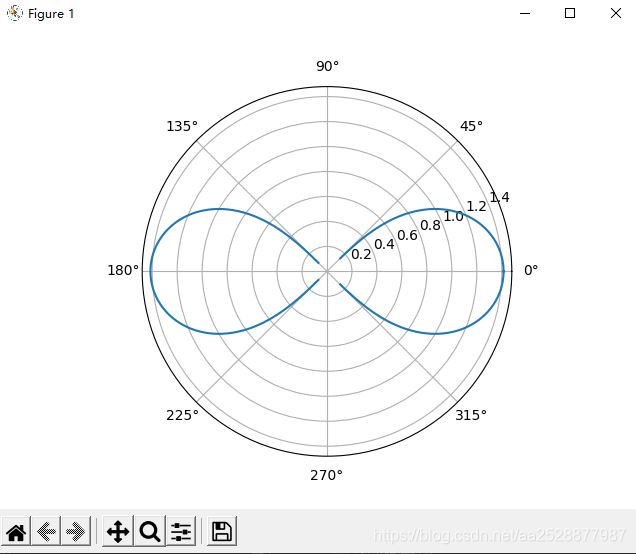
np.linspace来选取0到2π的1000个点，计算r，polar=True 为极坐标图

• NumPy 官网 http://www.numpy.org/
• NumPy 源代码：https://github.com/numpy/numpy
• SciPy 官网：https://www.scipy.org/
• SciPy 源代码：https://github.com/scipy/scipy
• Matplotlib 官网：https://matplotlib.org/
• Matplotlib 源代码：https://github.com/matplotlib/matplotlib