Eigenfaces
The problem with the image representation we are given is its high dimensionality. Two-dimensional 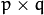 grayscale images span a
grayscale images span a 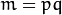 -dimensional vector space, so an image with
-dimensional vector space, so an image with 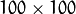 pixels lies in a
pixels lies in a 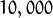 -dimensional image space already. The question is: Are all dimensions equally useful for us? We can only make a decision if there’s any variance in data, so what we are looking for are the components that account for most of the information. The Principal Component Analysis (PCA) was independently proposed by Karl Pearson (1901) and Harold Hotelling (1933) to turn a set of possibly correlated variables into a smaller set of uncorrelated variables. The idea is, that a high-dimensional dataset is often described by correlated variables and therefore only a few meaningful dimensions account for most of the information. The PCA method finds the directions with the greatest variance in the data, called principal components.
-dimensional image space already. The question is: Are all dimensions equally useful for us? We can only make a decision if there’s any variance in data, so what we are looking for are the components that account for most of the information. The Principal Component Analysis (PCA) was independently proposed by Karl Pearson (1901) and Harold Hotelling (1933) to turn a set of possibly correlated variables into a smaller set of uncorrelated variables. The idea is, that a high-dimensional dataset is often described by correlated variables and therefore only a few meaningful dimensions account for most of the information. The PCA method finds the directions with the greatest variance in the data, called principal components.
Algorithmic Description
Let 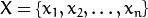 be a random vector with observations
be a random vector with observations 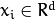 .
.
- Compute the mean
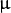
- Compute the the Covariance Matrix S
- Compute the eigenvalues
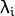 and eigenvectors
and eigenvectors 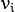 of
of 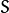
- Order the eigenvectors descending by their eigenvalue. The
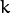 principal components are the eigenvectors corresponding to the
principal components are the eigenvectors corresponding to the 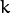 largest eigenvalues.
largest eigenvalues.
The 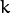 principal components of the observed vector
principal components of the observed vector 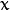 are then given by:
are then given by:
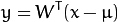
where 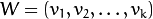 .
.
The reconstruction from the PCA basis is given by:
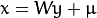
where 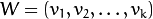 .
.
The Eigenfaces method then performs face recognition by:
- Projecting all training samples into the PCA subspace.
- Projecting the query image into the PCA subspace.
- Finding the nearest neighbor between the projected training images and the projected query image.
Still there’s one problem left to solve. Imagine we are given 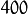 images sized
images sized 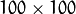 pixel. The Principal Component Analysis solves the covariance matrix
pixel. The Principal Component Analysis solves the covariance matrix 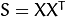 , where
, where 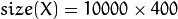 in our example. You would end up with a
in our example. You would end up with a 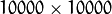 matrix, roughly
matrix, roughly 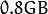 . Solving this problem isn’t feasible, so we’ll need to apply a trick. From your linear algebra lessons you know that a
. Solving this problem isn’t feasible, so we’ll need to apply a trick. From your linear algebra lessons you know that a  matrix with
matrix with 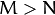 can only have
can only have 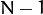 non-zero eigenvalues. So it’s possible to take the eigenvalue decomposition
non-zero eigenvalues. So it’s possible to take the eigenvalue decomposition 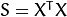 of size
of size  instead:
instead:
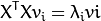
and get the original eigenvectors of 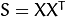 with a left multiplication of the data matrix:
with a left multiplication of the data matrix:
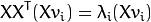
The resulting eigenvectors are orthogonal, to get orthonormal eigenvectors they need to be normalized to unit length. I don’t want to turn this into a publication, so please look into[Duda01] for the derivation and proof of the equations.
示例:
输入200张50x100图像,reshape成Mat(200,5000)
均值维度(1,5000)
特征值维度(min(n,200,5000),1)//n:配置的主成分个数
特征向量维度(min(n,200,5000),5000)








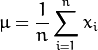
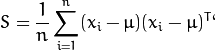
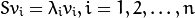













 1689
1689











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








