很多人都有误解,以为深度学习比机器学习先进。其实深度学习是机器学习的一个分支。可以理解为具有多层结构的模型。具体的话,深度学习是机器学习中的具有深层结构的神经网络算法,即机器学习>神经网络算法>深度神经网络(深度学习)。
关于深度学习的理论推导,太大太复杂,一些常见的深度学习算法本人也是模模糊糊的,看过好多次的,隔断时间就会忘记,现在对其系统的整理一下(从历史,致命问题出发,再看具体算法的思想,框架,优缺点和改进的方向,又总结了CNN和RNN的比较)。
一、历史:多层感知机到神经网络,再到深度学习
神经网络技术起源于上世纪五、六十年代,当时叫感知机(perceptron),拥有输入层、输出层和一个隐含层。输入的特征向量通过隐含层变换达到输出层,在输出层得到分类结果。(扯一个不相关的:由于计算技术的落后,当时感知器传输函数是用线拉动变阻器改变电阻的方法机械实现的,脑补一下科学家们扯着密密麻麻的导线的样子…)
心理学家Rosenblatt提出的单层感知机有一个严重得不能再严重的问题,即它对稍复杂一些的函数都无能为力(比如最为典型的“异或”操作)。
这个缺点直到上世纪八十年代才被Rumelhart、Williams、Hinton、LeCun等人发明的多层感知机解决,多层感知机解决了之前无法模拟异或逻辑的缺陷,同时更多的层数也让网络更能够刻画现实世界中的复杂情形。
多层感知机可以摆脱早期离散传输函数的束缚,使用sigmoid或tanh等连续函数模拟神经元对激励的响应,在训练算法上则使用Werbos发明的反向传播BP算法。这就是我们现在所说的【神经网络】,BP算法也叫BP神经网络具体过程可参见我转载的文章(http://blog.csdn.net/abc200941410128/article/details/78708319)。
但是BP神经网络(多层感知机)面临在致命问题(见下节)。随着神经网络层数的加深,有两个重大问题:一是优化函数越来越容易陷入局部最优解,并且这个“陷阱”越来越偏离真正的全局最优。利用有限数据训练的深层网络,性能还不如较浅层网络。同时,另一个不可忽略的问题是“梯度消失”现象更加严重。
2006年,Hinton利用预训练方法缓解了局部最优解问题,将隐含层推动到了7层,神经网络真正意义上有了“深度”,由此揭开了深度学习的热潮,随后的DBN、CNN、RNN、LSTM等才逐渐出现。
这里的“深度”并没有固定的定义——在语音识别中4层网络就能够被认为是“较深的”,而在图像识别中20层以上的网络屡见不鲜。
为了克服梯度消失,ReLU、maxout等传输函数代替了sigmoid,形成了如今DNN的基本形式。单从结构上来说,全链接的多层感知机是没有任何区别的。
二、深度神经网络的致命问题
随着神经网络层数的加深,有三个重大问题:一是非凸优化问题,即优化函数越来越容易陷入局部最优解;二是(Gradient Vanish)梯度消失问题;三是过拟合问题。
2.1 非凸优化问题
线性回归,本质是一个多元一次函数的优化问题,设f(x,y)=x+y
多层神经网络,本质是一个多元K次函数优化问题,设f(x,y)=xy
在线性回归当中,从任意一个点出发搜索,最终必然是下降到全局最小值附近的。所以置0也无妨(这也是为什么我们往往解线性回归方程时初值为0)。
而在多层神经网络中,从不同点出发,可能最终困在局部最小值。局部最小值是神经网络结构带来的挥之不去的阴影,随着隐层层数的增加,非凸的目标函数越来越复杂,局部最小值点成倍增长,利用有限数据训练的深层网络,性能还不如较浅层网络。。避免的方法一般是权值初始化。为了统一初始化方案,通常将输入缩放到[−1,1],但是仍然无法保证能够达到全局最优,其实这也是科学家们一直在研究而未解决的问题。
所以,从本质上来看,深度结构带来的非凸优化仍然不能解决(包括现在的各类深度学习算法和其他非凸优化问题都是如此),这限制着深度结构的发展。
2.2 (Gradient Vanish)梯度消失问题
这个问题实际上是由激活函数不当引起的,多层使用Sigmoid系函数,会使得误差从输出层开始呈指数衰减。在数学上,激活函数的作用就是将输入数据映射到0到1上(tanh是映射-1到+1上)。至于映射的原因,除了对数据进行正则化外,大概是控制数据,使其只在一定的范围内。当然也有另外细节作用,例如Sigmoid(tanh)中,能在激活的时候,更关注数据在零(或中心点)前后的细小变化,而忽略数据在极端时的变化,例如ReLU还有避免梯度消失的作用。通常,Sigmoid(tanh)多用于全连接层,而ReLU多用于卷积层。
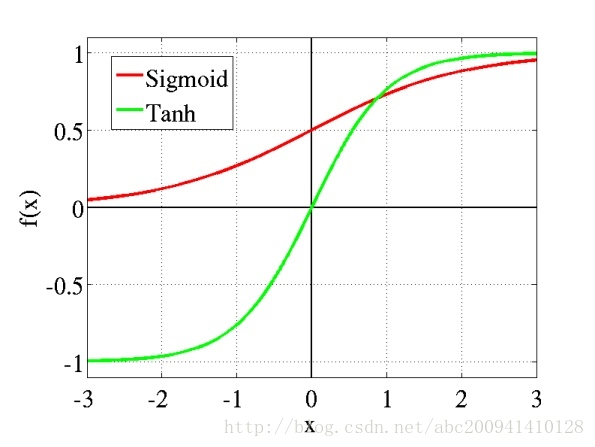
Sigmoid
ReLU
“梯度消失”现象具体来说,我们常常使用sigmoid作为神经元的输入输出函数。对于幅度为1的信号,在BP反向传播梯度时,每传递一层,梯度衰减为原来的0.25。层数一多,梯度指数衰减后低层基本上接受不到有效的训练信号。
幸运的是,这个问题已经被Hinton在2006年提出的逐层贪心预训练权值矩阵变向减轻,最近提出的ReLu则从根本上提出了解决方案。
2012年,Hinton组的Alex Krizhevsky率先将受到Gradient Vanish影响较小的CNN中大规模使用新提出的ReLu函数。
2014年,Google研究员贾扬清则利用ReLu这个神器,成功将CNN扩展到了22层巨型深度网络,见知乎。
对于深受Gradient Vanish困扰的RNN,其变种LSTM也克服了这个问题。
2.3 过拟合问题
这就是神经网络的最后一个致命问题:过拟合,庞大的结构和参数使得,尽管训练error降的很低,但是test error却高的离谱。
过拟合还可以和Gradient Vanish、局部最小值混合三打,具体玩法是这样的:
由于Gradient Vanish,导致深度结构的较低层几乎无法训练,而较高层却非常容易训练。
较低层由于无法训练,很容易把原始输入信息,没有经过任何非线性变换,或者错误变换推到高层去,使得高层解离特征压力太大。
如果特征无法解离,强制性的误差监督训练就会使得模型对输入数据直接做拟合。
其结果就是,A Good Optimation But a Poor Generalization,这也是SVM、决策树等浅层结构的毛病。
Bengio指出,这些利用局部数据做优化的浅层结构基于先验知识(Prior): Smoothness
即,给定样本(xi,yi),尽可能从数值上做优化,使得训练出来的模型,对于近似的x,输出近似的y。
然而一旦输入值做了泛型迁移,比如两种不同的鸟,鸟的颜色有别,且在图像中的比例不一,那么SVM、决策树几乎毫无用处。
因为,对输入数据简单地做数值化学习,而不是解离出特征,对于高维数据(如图像、声音、文本),是毫无意义的。
然后就是最后的事了,由于低层学不动,高层在乱学,所以很快就掉进了吸引盆中,完成神经网络三杀。
三、深度学习里面的基本模型
深度学习里面的基本模型大致分为了3类:多层感知机模型;深度神经网络模型和递归神经网络模型。其代表分别是DBN(Deep belief network) 深度信念网络、CNN(Convolution Neural Networks)卷积神经网络、RNN(Recurrent neural network) 递归神经网络。
3.1 DBN(Deep belief network) 深度信念网络
2006年,Geoffrey Hinton提出深度信念网络(DBN)及其高效的学习算法,即Pre-training+Fine tuning,并发表于《Science》上,成为其后深度学习算法的主要框架。DBN是一种生成模型,通过训练其神经元间的权重,我们可以让整个神经网络按照最大概率来生成训练数据。所以,我们不仅可以使用DBN识别特征、分类数据,还可以用它来生成数据。
3.1.1 网络结构
深度信念网络(DBN)由若干层受限玻尔兹曼机(RBM)堆叠而成,上一层RBM的隐层作为下一层RBM的可见层。
(1) RBM
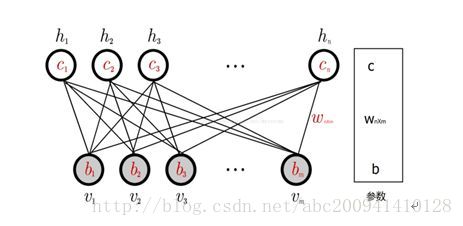
一个普通的RBM网络结构如上图所示,是一个双层模型,由m个可见层单元及n个隐层单元组成,其中,层内神经元无连接,层间神经元全连接,也就是说:在给定可见层状态时,隐层的激活状态条件独立,反之,当给定隐层状态时,可见层的激活状态条件独立。这保证了层内神经元之间的条件独立性,降低概率分布计算及训练的复杂度。RBM可以被视为一个无向图模型,可见层神经元与隐层神经元之间的连接权重是双向的,即可见层到隐层的连接权重为W,则隐层到可见层的连接权重为W’。除以上提及的参数外,RBM的参数还包括可见层偏置b及隐层偏置c。RBM可见层和隐层单元所定义的分布可根据实际需要更换,包括:Binary单元、Gaussian单元、Rectified Linear单元等,这些不同单元的主要区别在于其激活函数不同
(2) DBN
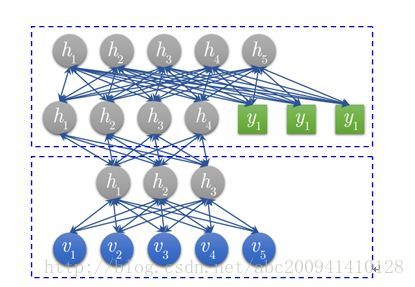
DBN模型由若干层RBM堆叠而成,如果在训练集中有标签数据,那么最后一层RBM的可见层中既包含前一层RBM的隐层单元,也包含标签层单元。假设顶层RBM的可见层有500个神经元,训练数据的分类一共分成了10类,那么顶层RBM的可见层有510个显性神经元,对每一训练数据,相应的标签神经元被打开设为1,而其他的则被关闭设为0
3.1.2 训练过程和优缺点
DBN的训练包括Pre-training和Fine tuning两步,其中Pre-training过程相当于逐层训练每一个RBM,经过Pre-training的DBN已经可用于模拟训练数据,而为了进一步提高网络的判别性能, Fine tuning过程利用标签数据通过BP算法对网络参数进行微调。
对DBN优缺点的总结主要集中在生成模型与判别模型的优缺点总结上。
1、优点:
- 生成模型学习联合概率密度分布,所以就可以从统计的角度表示数据的分布情况,能够反映同类数据本身的相似度;
- 生成模型可以还原出条件概率分布,此时相当于判别模型,而判别模型无法得到联合分布,所以不能当成生成模型使用。
2、缺点:
- 生成模型不关心不同类别之间的最优分类面到底在哪儿,所以用于分类问题时,分类精度可能没有判别模型高;
- 由于生成模型学习的是数据的联合分布,因此在某种程度上学习问题的复杂性更高。
- 要求输入数据具有平移不变性。
关于 判别模型与生成模型可以参看(http://blog.csdn.net/erlib/article/details/53585134)
3.1.3 改进模型
DBN的变体比较多,它的改进主要集中于其组成“零件”RBM的改进,有卷积DBN(CDBN)和条件RBM(Conditional RBM)等。
DBN并没有考虑到图像的二维结构信息,因为输入是简单的将一个图像矩阵转换为一维向量。而CDBN利用邻域像素的空域关系,通过一个称为卷积RBM(CRBM)的模型达到生成模型的变换不变性,而且可以容易得变换到高维图像。
DBN并没有明确地处理对观察变量的时间联系的学习上,Conditional RBM通过考虑前一时刻的可见层单元变量作为附加的条件输入,以模拟序列数据,这种变体在语音信号处理领域应用较多。
3.2 CNN(Convolution Neural Networks)卷积神经网络
卷积神经网络是人工神经网络的一种,已成为当前语音分析和图像识别领域的研究热点。它的权值共享网络结构使之更类似于生物神经网络,降低了网络模型的复杂度,减少了权值的数量。该优点在网络的输入是多维图像时表现的更为明显,使图像可以直接作为网络的输入,避免了传统识别算法中复杂的特征提取和数据重建过程。
全链接DNN的结构里下层神经元和所有上层神经元都能够形成连接,带来了参数数量的膨胀问题。例如,1000*1000的像素图像,光这一层就有10^12个权重需要训练。此时我们可以用卷积神经网络CNN,对于CNN来说,并不是所有上下层神经元都能直接相连,而是通过“卷积核”作为中介。同一个卷积核在所有图像内是共享的,图像通过卷积操作后仍然保留原先的位置关系。图像输入层到隐含层的参数瞬间降低到了100*100*100=10^6个
卷积网络是为识别二维形状而特殊设计的一个多层感知器,这种网络结构对平移、比例缩放、倾斜或者共他形式的变形具有高度不变性。
3.2.1 网络结构
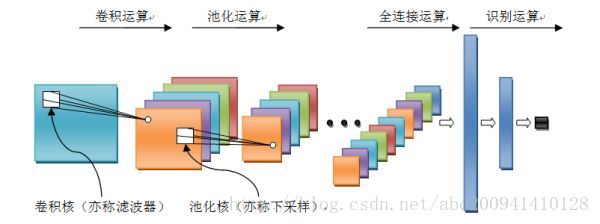
卷积神经网络是一个多层的神经网络,其基本运算单元包括:卷积运算、池化运算、全连接运算和识别运算。
- 卷积运算:前一层的特征图与一个可学习的卷积核进行卷积运算,卷积的结果经过激活函数后的输出形成这一层的神经元,从而构成该层特征图,也称特征提取层,每个神经元的输入与前一层的局部感受野相连接,并提取该局部的特征,一旦该局部特征被提取,它与其它特征之间的位置关系就被确定。l
- 池化运算:能很好的聚合特征、降维来减少运算量。它把输入信号分割成不重叠的区域,对于每个区域通过池化(下采样)运算来降低网络的空间分辨率,比如最大值池化是选择区域内的最大值,均值池化是计算区域内的平均值。通过该运算来消除信号的偏移和扭曲。
- 全连接运算:输入信号经过多次卷积核池化运算后,输出为多组信号,经过全连接运算,将多组信号依次组合为一组信号。
识别运算:上述运算过程为特征学习运算,需在上述运算基础上根据业务需求(分类或回归问题)增加一层网络用于分类或回归计算。
3.2.2 训练过程和优缺点
卷积网络在本质上是一种输入到输出的映射,它能够学习大量的输入与输出之间的映射关系,而不需要任何输入和输出之间的精确的数学表达式,只要用已知的模式对卷积网络加以训练,网络就具有输入输出对之间的映射能力。卷积网络执行的是有监督训练,所以其样本集是由形如:(输入信号,标签值)的向量对构成的。
1、优点:
- 权重共享策略减少了需要训练的参数,相同的权重可以让滤波器不受信号位置的影响来检测信号的特性,使得训练出来的模型的泛化能力更强;
- 池化运算可以降低网络的空间分辨率,从而消除信号的微小偏移和扭曲,从而对输入数据的平移不变性要求不高。
2、缺点:
- 深度模型容易出现梯度消散问题。
3.2.3 改进模型
卷积神经网络因为其在各个领域中取得了好的效果,是近几年来研究和应用最为广泛的深度神经网络。比较有名的卷积神经网络模型主要包括1986年Lenet,2012年的Alexnet,2014年的GoogleNet,2014年的VGG,2015年的Deep Residual Learning。这些卷积神经网络的改进版本或者模型的深度,或者模型的组织结构有一定的差异,但是组成模型的机构构建是相同的,基本都包含了卷积运算、池化运算、全连接运算和识别运算。
3.3 RNN(Recurrent neural network) 递归神经网络
全连接的DNN除了以上问题以外还存在着另一个问题——无法对时间序列上的变化进行建模。然而,样本出现的时间顺序对于自然语言处理、语音识别、手写体识别等应用非常重要。对了适应这种需求,就出现了题主所说的另一种神经网络结构——循环神经网络RNN(不知道为什么很多叫循环的。计算机术语里循环一般是同一层次的,Recurrent 其实是时间递归,所以本文叫他递归神经网络)。
在普通的全连接网络或CNN中,每层神经元的信号只能向上一层传播,样本的处理在各个时刻独立,因此又被成为前向神经网络(Feed-forward Neural Networks)。而在RNN中,神经元的输出可以在下一个时间戳直接作用到自身。
即:(t+1)时刻网络的最终结果O(t+1)是该时刻输入和所有历史共同作用的结果。RNN可以看成一个在时间上传递的神经网络,它的深度是时间的长度!正如我们上面所说,“梯度消失”现象又要出现了,只不过这次发生在时间轴上
为了解决时间上的梯度消失,机器学习领域发展出了长短时记忆单元(LSTM),通过门的开关实现时间上记忆功能,并防止梯度消失。
3.3.1 网络结构
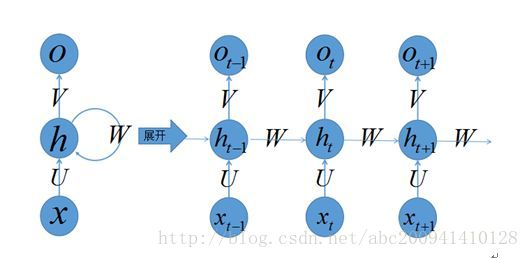
左侧是递归神经网络的原始结构,如果先抛弃中间那个令人生畏的闭环,那其实就是简单“输入层=>隐藏层=>输出层”的三层结构,但是图中多了一个非常陌生的闭环,也就是说输入到隐藏层之后,隐藏层还会输入给自己,使得该网络可以拥有记忆能力。我们说递归神经网络拥有记忆能力,而这种能力就是通过W将以往的输入状态进行总结,而作为下次输入的辅助。可以这样理解隐藏状态:h=f(现有的输入+过去记忆总结)
3.3.2 训练过程和优缺点
递归神经网络中由于输入时叠加了之前的信号,所以反向传导时不同于传统的神经网络,因为对于时刻t的输入层,其残差不仅来自于输出,还来自于之后的隐层。通过反向传递算法,利用输出层的误差,求解各个权重的梯度,然后利用梯度下降法更新各个权重。
1、优点:
- 模型是时间维度上的深度模型,可以对序列内容建模。
2、缺点:
- 需要训练的参数较多,容易出现梯度消散或梯度爆炸问题;
- 不具有特征学习能力。
3.3.3 改进模型
递归神经网络模型可以用来处理序列数据,递归神经网络包含了大量参数,且难于训练(时间维度的梯度消散或梯度爆炸),所以出现一系列对RNN优化,比如网络结构、求解算法与并行化。
近年来bidirectional RNN (BRNN)与 LSTM在image captioning, language translation, and handwriting recognition这几个方向上有了突破性进展 。
3.4 混合结构
除了以上三种网络,和我之前提到的深度残差学习、LSTM外,深度学习还有许多其他的结构。举个例子,RNN既然能继承历史信息,是不是也能吸收点未来的信息呢?因为在序列信号分析中,如果我能预知未来,对识别一定也是有所帮助的。因此就有了双向RNN、双向LSTM,同时利用历史和未来的信息。双向RNN、双向LSTM,同时利用历史和未来的信息。
事实上,不论是那种网络,他们在实际应用中常常都混合着使用,比如CNN和RNN在上层输出之前往往会接上全连接层,很难说某个网络到底属于哪个类别。
不难想象随着深度学习热度的延续,更灵活的组合方式、更多的网络结构将被发展出来。尽管看起来千变万化,但研究者们的出发点肯定都是为了解决特定的问题。如果想进行这方面的研究,不妨仔细分析一下这些结构各自的特点以及它们达成目标的手段。
3.5 CNN和RNN的比较
RNN的重要特性是可以处理不定长的输入,得到一定的输出。当你的输入可长可短, 比如训练翻译模型的时候, 你的句子长度都不固定,你是无法像一个训练固定像素的图像那样用CNN搞定的。而利用RNN的循环特性可以轻松搞定。
在序列信号的应用上,CNN是只响应预先设定的信号长度(输入向量的长度),RNN的响应长度是学习出来的。
CNN对特征的响应是线性的,RNN在这个递进方向上是非线性响应的。这也带来了很大的差别。
CNN 专门解决图像问题的,可用把它看作特征提取层,放在输入层上,最后用MLP 做分类。
RNN 专门解决时间序列问题的,用来提取时间序列信息,放在特征提取层(如CNN)之后。
RNN,递归型网络,用于序列数据,并且有了一定的记忆效应,辅之以lstm。
CNN应该侧重空间映射,图像数据尤为贴合此场景。
CNN 卷积擅长从局部特征逼近整体特征,
RNN 擅长对付时间序列。
四、一些基本概念和知识
4.1 线性回归、线性神经网络、Logistic/Softmax回归
这个参考http://blog.csdn.net/erlib/article/details/53585134
或者其他资料。
4.2 关于卷积、池化、激活函数等
入门参考:http://blog.csdn.net/u010859498/article/details/78794405
详细了解可自己谷歌百度
4.3 推荐一个比较好的入门资料
台大电机系李宏毅教授的讲义《一天搞懂深度学习》
有人做简略的翻译过
https://www.jianshu.com/p/c30f7c944b66
参考资料:
http://blog.csdn.net/erlib/article/details/53585134
https://www.zhihu.com/question/34681168/answer/156552873
http://blog.csdn.net/u010859498/article/details/78794405
























 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








