拼多多今年社招一面试题！

最新推荐文章于 2024-06-26 11:05:18 发布

数据结构和算法

最新推荐文章于 2024-06-26 11:05:18 发布

阅读量1.6k

点赞数 22

文章标签：算法

本文链接：https://blog.csdn.net/abcdef314159/article/details/134985814

版权

算法学习网址：wansuanfa.com (玩算法的拼音)

这题是LeetCode的第33题，难度为中等，应该说不算难，一网友在今年拼多多的社招面试中遇到这题，除了拼多多考这道题以外，我们看到微软，360，字节，快手等都考过。

其中一网友在微软的面试中因为这题的边界条件忘记判断被拒，真的是很遗憾，以后做题还是要认真一些。我一直以为像微软这样的大厂面试应该是非常难的，没想到这种中等的题也会考，下面我们就来看下这道题。

问题描述

来源：LeetCode第33题

难度：中等

整数数组 nums 按升序排列，数组中的值互不相同。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标从 0 开始计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你旋转后的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例1：

输入：nums = [4,5,6,7,0,1,2], target = 0

输出：4

示例2：

输入：nums = [4,5,6,7,0,1,2], target = 3

输出：-1

问题分析

这题说的是一个有序数组，数组中的值都不相同，但在某个位置进行了旋转，然后给定一个值target，让我们查找target，但是查找的时候有条件限制，就是查找的时间复杂度是O(log n)。

如果没有这个条件限制，我们可以一个个查询，时间复杂度是O(n)。但因为有这个条件的限制，我们可以考虑使用折半查找，也就是二分查找。

一般情况下如果使用二分查找数组必须是有序的，但这里的有序数组被旋转了一下，没关系，我们依然可以使用二分查找。注意这里中间值mid指向的值和target比较的时候要分4种情况，我们画个图来看下。

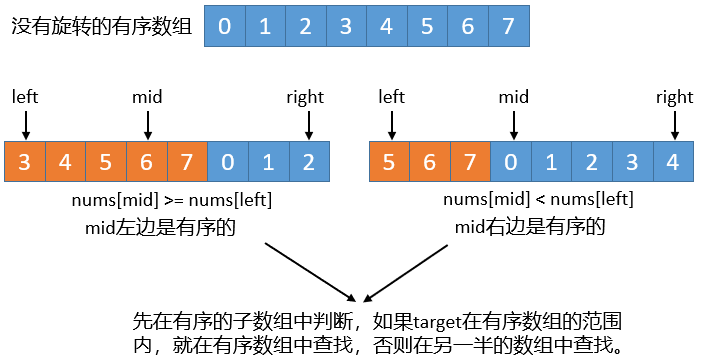
这里再来说下，如果nums[mid] >= nums[left]，说明mid左边是有序的，因为有序数组是递增的，只有有序的情况下nums[mid]才会大于等于nums[left]。

否则也就是nums[mid] < nums[left]，如果是有序数组nums[mid]不可能小于nums[left]，如果nums[mid]的值小于nums[left]，说明在left到mid之间出现了旋转。

最后我们再来看下代码：

public int search(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = (left + right) >>> 1;
        if (nums[mid] == target)// 如果找到直接返回下标。
            return mid;
        if (nums[mid] >= nums[left]) {// 左边是有序的。
            // 再判断 target 是在 mid 的左边还是右边，从而调整左右边界。
            if (target >= nums[left] && target < nums[mid]) {
                right = mid - 1;// 在mid的左边
            } else {
                left = mid + 1;// 在mid的右边
            }
        } else {//右边是有序的，同上
            if (target > nums[mid] && target <= nums[right]) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
    }
    return -1;
}

-------------------------end-------------------------

笔者简介

博哥，真名：王一博，毕业十多年，《算法秘籍》作者，专注于数据结构和算法的讲解，在全球30多个算法网站中累计做题2000多道，在公众号中写算法题解700多题，对算法题有自己独特的解题思路和解题技巧，喜欢的可以给个关注，也可以下载我整理的1000多页的PDF算法文档。