故障诊断学习

信号处理&故障诊断

Dsp相关

时域

帧长度/frame size -------------------- T

时间间隔/时间分辨率 ---------------- $$\Delta t$$

数据块大小(分析点数) ---------------- N

频域

采样（频）率 -------------------------- fs

最大频率/带宽 ------------------------ $$f_{max}$$

频率分辨率 --------------------------- $$\Delta f$$

谱线数-------------------------------- N/2

1.帧长度/frame size：T

进行一次FFT分析所截取的时域信号长度，称为1帧数据或frame size，单位为s，也称1个时域数据块。由于实际采集的时域信号时间很长，而一次FFT分析只能分析有限长度的时域信号，因此，需要将采样时间很长的时域信号截断成一帧一帧的frame size。这个截取过程叫做信号截断。而信号截断又分为周期截断和非周期截断。

假设有一段10s的时域信号，取1帧的长度 T = 1s ，无重叠，则该信号将被截断为10帧，如下图所示。按此规律进行FFT计算，将得到10个瞬时频谱，如果将这些瞬时频谱进行平均，那么平均次数为10次，最终的FFT分析结果为这10个瞬时频谱的平均结果。

以上截取是没有考虑信号重叠的，有时会用百分比来表示重叠，若重叠率为50%，表示这一帧信号将与下一帧信号有50%是共用的。也就是第一帧的后50%作为第二帧的前50%。有时也用时间增量或转速增量来表示，在这以时间增量为例进行说明。我们每截取的一帧时间长度是固定的，但是隔多长时间截取一帧呢？这个隔多长时间截取一帧，就是所谓的步长或增量(increment)，如下图所示。

当增量小于frame size时，相邻两帧数据之间有重叠，重叠率计算公式如下

重叠率 = *(frame size – increment)/frame size 100%

当增量等于frame size时，相邻两帧数据之间无重叠，但两帧数据刚好无缝连接，如第一个图所示。

当增量大于frame size时，相邻两帧数据之间无重叠，但两帧数据之间有间隙，也就是有部分时域数据是不参与FFT计算的。

2. 时间间隔&时间分辨率： $$\Delta t$$

相邻两个时域数据点的采样时间差，称为时间间隔，等于采样频率的倒数，单位为s。时间间隔越小，采样率越高，采样越密集，信号越接近真实信号，时间间隔如下图所示。假设采样频率为1000Hz，则时间分辨率为1ms，表示采集两个数据点的时间间隔为1ms，同时表明1s采集1000个数据点。时间分辨率是指信号在时间轴上的分辨能力，时间间隔是两个采样点之间的时间差。

3. 数据块大小： N

一帧数据所对应的数据点数（样本点，分析点数），称为时域数据块大小（time block size），如上图中黑色实心点，即表示1个数据点。因此，一帧数据除用时间长度来描述之外，也可以用数据点数来描述。它们之间的关系如下：
$$T=N\ast \Delta t$$
因此，一帧数据包含多少个数据点，是可以计算出来的。有的软件不是通过设置频率分辨率的大小来决定一帧数据的长度（等于频率分辨率的倒数），而是通过设置数据块大小 来决定一帧数据的长度。

4. 采样率： $$fs$$

由于计算机不能处理模拟信号，因此，必须通过采样将模拟信号转换成数字信号。用来表征采样快慢的参数称为采样（频）率，单位为Hz。本质上，称呼采样频率为采样率更合适，因为它表征的是采样的速率，采样率高，则采样快。采样率是表示每秒钟采集多少个样本点（或数据点），也可用sample/s或样本点数/秒表示。

采样频率越高，采两个样本点的时间间隔越短，采集到的数字信号越接近真实信号。

5.最大频率/带宽： $$fmax$$

采样频率的一半，称为带宽，或最大分析频率，或奈奎斯特频率。它与采样率的关系如下
$$fmax=fs/2$$
也就是说，最终分析出来的所有频率都位于带宽以内，哪怕是存在频率混叠，呈现出来的频率也在这个区间。因此，为了防止高于带宽以上的频率成分混叠到带宽以内，需要在模数转换前进行抗混叠滤波。

6. 频率间隔：$$\Delta f$$

我们已经明白采集到的时域信号是离散的，两个时域数据点的时间差称为时间间隔。同理，频谱也是离散的，相邻两条谱线的频率差或频率间隔。FFT计算得到的结果只位于频率分辨率的整数倍处，也就是谱线处，其他地方无结果，如下图所示。假设图中的虚线为谱线，各条谱线对应的频率为频率分辨率的整数倍。计算得到的频谱结果只位于这样的谱线处。

频率结果只能位于各条谱线上，谱线与谱线之间是没有结果的，频谱的这种离散效应，称为栅栏效应。就好像人们通过篱笆看外面的世界一样，只能通过相邻两块篱笆之间的缝隙看到外面的世界，而篱笆却挡住了人们的视线。那么，相邻两块篱笆之间的缝隙比拟为频谱图中的谱线，也只有谱线上才有数据，谱线之间的区域是没有结果的，如下图所示，只有谱线上才有红色的频率结果，最后的频谱曲线是根据这些谱线上的点连成的曲线。

频率间隔越大，相邻谱线间隔越远，因此，求得的频率误差越大。FFT分析时，频率误差最大不会大于半个频率间隔。因为频率是按四舍五入的原则归到最近的谱线上。频率间隔的倒数为做一次FFT所截断的时域信号的长度 ，也就是一帧数据长度。当频率间隔越小时，必然一帧数据的长度很大。因此，在做FFT计算时，不能设置过小的频率间隔，也不能设置过大的频率间隔，频率间隔过大可能导致频率误差加大。

另一方面，当对旋转机械进行瀑布图分析时，频率间隔的大小跟转速改变速率有关系。下图分别为0.5Hz（上）和5Hz（下）的频率间隔，计算同一升速信号的瀑布图结果。0.5Hz对应的时域数据块长度为2s，5Hz对应的时域数据块长度为0.2s，从图中可以看出，5Hz的频率分辨率下各阶次更明显，这是因为相应的时域数据块更短，在这个更短的时间内，转速变化没有0.5Hz对应的时域数据块的转速变化大，因此，频率更清晰。时域数据块越短，越可以认为在该时间段内信号是稳态信号。

因此，当做瀑布图分析时，需要根据转速的变化速率来选择合适的频率分辨率。更优的频率分辨率（频率间隔越小），频谱拖尾更严重，特别是在转速高的情况下。信号出现“拖尾”现象是因为信号的频率在采集时域数据块的过程中变化明显。故对于旋转机械的瀑布图分析，应着重注意频率分辨率对分析结果的影响。

7. 谱线数： N/2

频谱图中谱线的总条数，称为谱线数。也可以理解为带宽按频率分辨率进行等分，等分的份数即为谱线数。N个时域样本点的FFT得到N/2条谱线，也就是说两个时域数据点能得到一条谱线。

谱线数与带宽、频率分辨率的关系如下
$$N/2=fmax/\Delta f$$
由于这三者是相互关联的，因此，当进行数据采集时，只需要设置其中两个参数就可以了，第三个参数，自动变化为相对应的值。像在Testlab软件中，这三个参数的设置界面如下图所示。在这，建议大家设置带宽和频率分辨率这两个参数。因为设置了带宽后，采样频率也就确定了。频率分辨率确定后，谱线数也随之确定了。另外，设置频率分辨率更直观。

时间分辨率与采样频率的关系：
$$\Delta t=1/fs$$
帧长度与数据块大小、时间分辨率、采样频率和频率分辨率的关系：
$$T=N\ast \Delta t=N/fs=1/\Delta f$$
带宽与采样频率、频率分辨率、谱线数和帧长度的关系
$$fmax=fs/2=\Delta f\ast N/2=N/2\ast 1/T$$
频率分辨率与帧长度、采样频率、数据块大小、带宽和谱线数的关系
$$\Delta f=1/T=fs/N=fmax/(N/2)$$

通过上面的关系式，我们明白了频率分辨率与一帧数据长度的关系。减少一帧数据长度 T，相当于增大频率分辨率$$\Delta f$$ ，意味着差的频率分辨率。要想获得更优的频率分辨率$$\Delta f$$ ，相当于截取更长的时域数据 T，如下图所示，增加一帧数据长度T ，频率分辨率将减小，谱线更密，计算得到的频率更精确。

信号处理名词相关

振动噪声信号处理时，经常出现一些令人混淆的名称，如宽带与带宽、谱线与线谱和相关分析与相干分析等等，特别是对初学者而言，更难于理解。在这，将对这些易混淆的名称进行解释说明，使你明白它们之间的区别与联系。

1.模拟信号与数字信号

模拟信号是指在时间和幅值上都是连续变化的信号。表征的物理量是连续变化的，如某个位置的振动加速度、背景噪声、温度等。许多传感器输出的信号都是连续的模拟信号，但是模拟信号不能用于计算机处理。

数字信号指时间和幅值的取值都是离散的，用有限个离散的数字来表征连续变化的信号，则称为数字化。通常这些离散的数字用有限位（bit）的二进制数（0和1）来表示，方便计算机处理。

如下图所示，红色信号为随时间变化的连续模拟信号，为了方便在计算上处理这个信号，需要将它转化为数字信号，也就是从时间轴上对它进行采样。用这些离散的采样数据点（实心黑色点）来表征它，采样点之间的信息是没有的，因此，采样时会丢失很多信息。

2. 时域与频域

采集到的信号都是随时间变化的数字信号，如下图所示为加速度随时间变化曲线。这个信号横轴为时间，也就是说信号的幅值随时间变化，因而，可以说信号是时间的函数，因此，把这个信号称为时域信号。故时域是指以时间为变量的函数所在的域。

对时域信号进行FFT变换，得到的结果是幅值随频率的变化曲线，也就是以频率为变量的函数，因此，频域是指以频率为变量的函数所在的域。

3. 角度域与阶次域

对于旋转机械而言，如果采集信号的同时还采集了旋转轴的转速信号，那么，时间与角度是有对应关系的。因此，可以将时域信号转换到角度域，也就是说，此时信号是角度的函数，故角度域是指以角度为变量的函数所在的域。

对角度域的信号作FFT变换，得到的结果是幅值随阶次变化的函数，此时信号的横轴是阶次。因此，阶次域是指以阶次为变量的函数所在的域，所下图所示。

1. 阶次的物理意义

按照振动理论来分，可以把振动分成线振动和角振动。线振动是我们通常所说的常规的振动，用位移、速度和加速度来描述，对应的载荷是力；角振动是旋转振动或扭转振动，用角位移、角速度和角加速度来描述，对应的载荷是力矩或扭矩。一个刚体有6个自由度，分别为3个平动自由度和3个转动自由度，那么平动对应的是线振动，转动对应的是角振动。

对于常规的振动（线振动）而言，通常用频率来描述一秒钟内振动往复的次数，这就是所谓的振动频率。如图1所示，在一秒钟内有两个周期，因此，振动频率是2Hz，或者说一秒钟内振动这个事件发生的次数是2次。用时间和频率来描述常规的线振动。

图1 振动频率

对于扭转振动而言，通常用阶次这个名词来描述，阶次表示的是旋转部件每旋转一圈（360度）事件发生的次数。与阶次相对应的是角度或者旋转的圈数，而每旋转一圈对应360度，因此，圈数与角度是等价的。扭转振动中的阶次与圈数（或角度）对应于常规振动中的振动与时间。如图2所示，横轴表示圈数或角度，那么在一圈内振动的周期是2个，那么振动这个事件发生2次，我们可以说阶次是2阶次。因此，阶次的物理意义是表示每圈事件发生的次数。

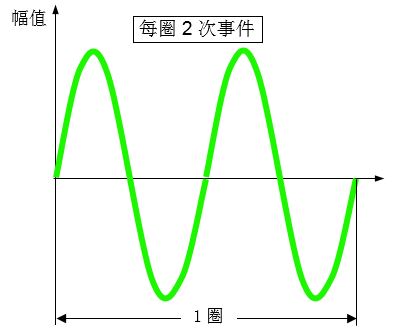
图2 阶次

4. 传递函数与频响函数

以部分分式的形式写出单自由系统的传递函数，形如

因为传递函数是复值函数，所以传递函数是两个变量σ和ω的函数，这两个变量分别是复平面的实部和虚部。

如果我们考虑系统传递函数的切片——频响函数，那么在σ=0时估计这个函数，也就是说传递函数沿频率jω轴估计。那么我们可以写出频响函数，形如

如果我们对比传递函数和频响函数的表达式，会发现在传递函数中独立变量是"s=σ+jω"，而频响函数中独立的变量是"jω"，因此，频响函数是传递函数的子集。

另一方面，传递函数表示的是输出与输入之比，不仅仅用于模态分析，还可用于其他领域，可用于为任何信号生成传递函数。测量信号可以是一般的信号，如电路分析、声学测量、传导性测量等等。自变量的取值可以是复平面上任意实部与虚部，并且实部与虚部可以表征任何物理量。而频响函数是响应与激励之比。响应是振动、噪声或应变信号，输入信号为力，体积加速度等，频响函数的取值只是虚部，虚部表示的物理量一定是频率，而非其他物理量。

5. 拉普拉斯域与傅立叶域

通过上面已经明显传递函数和频响的区别。传递函数的自变量是实部和虚部，而频响函数的自变量仅仅是虚轴。现在如果我们绘出传递函数所对应的曲线图，该图将映射成一个曲面，因为这个函数是通过两个独立变量σ和ω定义的。因为这些数值是复数，所以，我们可以分别绘出它们的实部和虚部图，当然也可以绘出函数的幅值和相位图。如用幅值来表示，那么将如下图蓝色区域所示。

在这，传递函数的自变量取值整个复平面，包括实部和虚部，因而，称以实部与虚部为自变量的函数所在的域为拉普拉斯域。之所以称为拉普拉斯域是因为对传递函数进行变换的方法是拉普拉斯变换。

如果我们考虑系统传递函数沿jω轴估计的幅值，并且将其投影到沿jω轴的切片平面上，那么我们将看到如上图所示的投影切片。而这正好是我们用FFT分析仪测量得到的曲线：频响函数。并且可以看出，这只有一个独立变量ω用于描述频响函数。同时，我们也注意到我们仅用一条曲线，而不是一个曲面来描述系统的频响函数。把以虚部（频率轴）为自变量的函数所在的域称为傅立叶域，之所以称傅立叶域，是因为变换方法为傅立叶变换。

频响函数是传递函数的特例，实际上我们也可以说傅立叶变换是拉普拉斯变换的特例。传递函数的自变量是整个复平面，也就是拉普拉斯域，而频响函数的自变量仅是沿虚轴，也就是沿频率轴，对应的是傅立叶域。

在这你可能会问：傅立叶域不就是沿频率轴变化，那么，它跟频域有什么区别呢？频域仅仅是随频率变化，是从实数的角度来考虑的。而傅立叶域是从复数的角度来考虑的，频率轴是以jω为变量，注意是复数j与频率ω的乘积。

6. 物理空间与模态空间

物理空间是指我们生活中的现实世界，而模态空间是指用模态来表征的模态坐标空间。从数学角度上讲，对物理空间上的运动方程通过特征值求解和模态变换方程，将这组物理空间上耦合的方程进行解耦，解耦后的方程为一组单自由度系统的运动方程，此时转换后的新坐标系统，称为模态空间。

因此，模态转换是将方程从物理空间通过模态转换方程转换到模态空间的过程；是将一组复杂的、耦合的物理方程转换成一组解耦的单自由度系统的过程。因而，我们可以将下图中的物理模型分解成一组单自由度系统，如图中所示的蓝色1阶、红色2阶和绿色3阶。模态空间使得我们更易于用单自由度系统去描述结构系统。

因此，模态转换是将方程从物理空间通过模态转换方程转换到模态空间的过程；是将一组复杂的、耦合的物理方程转换成一组解耦的单自由度系统的过程。因而，我们可以将下图中的物理模型分解成一组单自由度系统，如图中所示的蓝色1阶、红色2阶和绿色3阶。模态空间使得我们更易于用单自由度系统去描述结构系统。

在物理空间上任一位置测量得到的响应实际上是当前结构所受的激励力所激起来的模态空间中的各阶模态在当前测量位置产生的响应的叠加。

以上各种域或空间：时域与频域、角度域与阶次域、模态空间和物理空间并没有实质性的不同，仅仅是形式不同而已。每个域只是描述或者察看数据更方便。然而，有时从一个域察看某些信息会比其他的域更容易、更便捷。比如，总的时域响应不能确定有多少阶模态对结构的响应有贡献，但是频域的总的频响函数就能清楚地显示有多少阶模态被激起和每一阶模态对应的频率是多少。因此，我们经常将数据从一个域变换到另一个域，仅仅是因为数据更易于解释某些问题。

7. 阶与阶次

描述结构的固有频率或模态，通常用阶，而描述旋转机械通常用阶次。阶次是结构旋转部件因旋转造成的振动或/和噪声的响应，这个阶次响应与转速和转频之间有对应关系。确切地说阶次是转速或转频的倍数，对转速保持不变。独立于轴的实际转速，是参考轴转速的倍数或者分数。而结构的振动噪声响应通常出现在转速的倍数或者分数处，也就是这些阶次处。

而“阶”是结构固有属性的一种描述方式，跟外界的激励是没有关系的，描述的是结构的固有频率或模态有多少“阶”或第几“阶”。并且，一般是针对结构而言的，该结构可以是旋转结构，也可以不是旋转结构。而阶次一定是针对旋转结构而言的，只有当结构处于旋转激励时，我们才谈阶次，此时，也经常将阶次简称阶，但不是我们描述结构固有属性所说的那个“阶”。

如下面左侧瀑布图中斜线是我们所说的某阶次，右侧垂直频率轴的亮线或峰值是共振频率，对应某阶固有频率。阶用来描述固有频率或模态，阶次用来描述响应与转速或转频的倍数关系。

8. 共振频率与固有频率

共振是指系统受到外界激励时产生的响应表现为大幅度的振动，此时外界激励频率与系统的固有频率相同或者非常接近。共振是一种现象，共振发生时的频率称为共振频率。不管共振发生与否，结构的固有频率是不变的，而只有当外界的激励频率接近或等于系统的固有频率时，系统才发生共振现象。

当结构的阻尼非常小时，共振频率近似等于结构的固有频率，也是材料自身分子的自由振动频率。因而，单个共振是外界的激励频率等于或非常接近结构或材料的固有频率时，结构或材料发生大幅度的振动。当激励频率与固有频率相等或接近时，才发生共振。因而，共振频率不一定完全与固有频率相等，共振频率是从外界的激励频率来讲的，而固有频率是从结构属性来讲的。虽然很多情况下，都认为共振频率就是固有频率。

在频响函数曲线中，共振峰所对应的频率为结构的固有频率。但很多情况，共振不是发生在单一频率（固有频率）处，而是具有一定宽度的共振带。也就是存在一个频率区间，在这个区间内很容易发生共振。在colormap图中，经常可以看到如下所示的垂直频率轴的具有一定宽度的高亮区域，这个区域就是所谓的共振带区域。这个区域一定是在结构的某一阶固有频率附近。从下图可以看出，共振频率具有一定带宽，而结构的固有频率一定是一个单值频率。

9. 基频与主频

基频是指结构的第一阶固有频率。结构发生振动时，通常不会是以某一个频率振动，而是有多个振动频率，通常在这些振动频率中，能量最大的振动频率称为主频。因此，这个主频可能是结构的固有频率，也可能是强迫响应频率。

如下图所示的PSD曲线中，存在三个峰值（假设都是固有频率），因而这三个峰值对应三阶固有频率，其中最低阶的固有频率为基频，峰值最大的频率为主频。基频一定是固有频率，主频可能不一定是结构的固有频率，主频主要看的是能量的大小。因为我们知道，当结构产生强迫振动时，振动的频率是与外界激励频率相等的，但此时，这个激励频率很大程度上不是结构的固有频率，而它的能量又是最大的，此时，主频就不是固有频率。

10. AC与DC

AC和DC是交流和直流耦合的简称，在选择输入模式时，可能选择不同的耦合方式会影响到数据中的频率成分。大多数信号都有AC成分和DC成分，DC成分是0Hz的部分，对应时域信号中的直流分量（或称为直流偏置），AC成分是信号中的交变部分，包含信号中所有的非零频率成分，如下图所示。

如上图所示，交变的AC部分围绕DC偏置波动，有时称这个直流分量DC部分为基线，即信号围绕基线波动。对直流偏置进行FFT分析，得到0Hz的成分。对交变部分进行FFT分析，则得到信号中的非零频率成分。

AC耦合只允许信号中的交变部分通过，将移除信号中的直流分量（DC部分），通常使用隔直电容器实现。AC耦合可有效地阻隔掉信号中的DC部分，使信号的平均值为0。DC耦合同时允许信号中的交变部分（AC）和直流分量（DC）通过。因此，当选择不同的耦合方式时，会影响到信号中直流偏置（实际上还有少量低频成分）。

11.带宽与宽带

FFT分析时，信号分析的最大频率范围称为带宽，通常是采样频率的一半，如下图所示，分析的最高频率为4096Hz，因此，带宽为4096Hz。也就是说带宽是频谱分析时能观测到的最大频率上限。

宽带是指信号的频率分布，若信号频率范围很广（信号频率成分是连续的），可以认为是一个宽带信号。对于锤击法而言，则是一种宽带激励技术，这是因为力脉冲对应的力谱是一个连续的宽频信号，能激起很宽的频率区间内的模态。

带宽和宽带都可以认为是一个频率区间，但带宽一定是指这样一个频率区间：0-半个采样频率；而宽带是指信号的频率分布在一个连续的宽频带。

12. 宽带与窄带

与宽带相对应的是窄带，假设信号的频率宽度为B，中心频率为f0，如下图所示。通常认为窄带信号满足以下要求：信号的频率宽度B远小于中心频率f0，通常要求B/f0<0.1。例如，单频信号则属于窄带信号，以及我们大多数情况下测量的信号只包含若干个单频成分，那么这也是窄带信号，对应的频谱称为窄带谱。如使用步进正弦进行激励时，则这种激励技术是一种窄带激励技术，因为每一时刻只有一个频率成分。

另外，也可以从频率成分来理解宽带与窄带，若信号相邻频率成分相差很小，则可认为是一个宽带信号，如宽带随机信号；若相邻频率成分相差甚远，则属于窄带信号，如正弦信号。

宽带与窄带并没有严格的区分，如信号频率宽度多少以下为窄带，多少以上为宽带。因此，二者是一个相对的概念。

13. 谱线与线谱

FFT分析得到的频谱不是连续的，而是离散的，相邻两个离散频率点的间距为一个频率分辨率，这些离散的频率点对应一条条谱线。或者说，带宽按频率分辨率来划分，划分了很多等份，每个等分处为一条谱线，如下图中的虚线所示，这些谱线处的频率是频率分辨率的整数倍。若带宽为400Hz，频率分辨率为1Hz，则有400条谱线，频率对应1-400之间的自然数。FFT计算得到的结果只分布在这些谱线上，其他地方没有数值。这些谱线并不是真实的线条，而只是代表在这个位置有一个FFT计算数值。

线谱是指信号的频率成分近似一条直线，如对正弦波做FFT分析，如果信号截断刚好是周期的整数倍，那么，得到的频谱结果就是线谱，如下图所示，线谱是从频谱的形状上来说的。

14.平均

平均是指对各帧时域数据的频谱（图中的S表示FFT频谱）进行平均，最后得到平均的频谱结果。对瞬时频谱进行平均时，不是最后才进行平均，而是边计算边进行平均。如下图所示，第一帧数据的频谱结果S1与第二帧数据的频谱结果S2进行第一次平均得到平均的结果A1，然后A1再与第三帧数据的频谱结果S3进行第二次平均，得到结果A2，如此进行，直到与最后一帧数据的频谱结果进行平均，得到最终的结果为止。

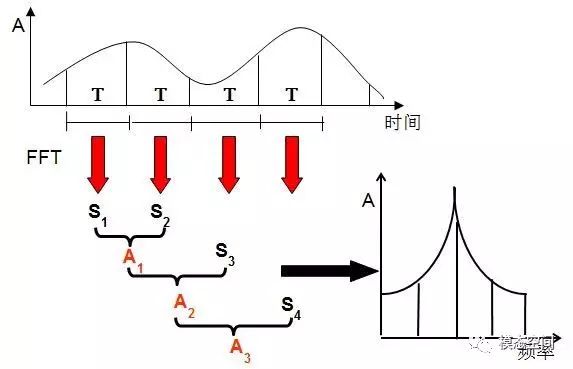
​ 频谱平均示意图

平均的方式有很多种，如线性平均、能量平均、指数平均等，每一种平均方式计算公式都是不一样的，因此，做FFT平均时，还需要选择合适的平均方式。

15. 重叠与步长

FFT分析只能对有限长度的时域信号进行变换，当频率分辨率确定以后，每次FFT变换的时域数据块长度是固定不变的，或者说一帧数据的长度（Frame Size）是固定的，等于频率分辨率的倒数。因此，FFT分析所截取的时域信号长度是固定的，但每次如何截取这一段固定长度的时域信号，就可能会采用不同的方式了。常见的方式有重叠和步长（时间步长或转速步长）。

如果采用重叠的方式，通常用百分比来表示重叠，表示相邻两帧数据之间重叠的比例。如重叠50%，表示这一帧的信号将与下一帧的信号有50%是共用的。也就是第一帧的后50%作为第二帧的前50%。

如果用步长(incement)的方式，又分为时间步长和转速步长，在这以时间步长为例进行说明。我们每截取的一帧数据时间长度是固定的，但是隔多长时间截取一帧呢？这个隔多长时间截取一帧，就是所谓的步长或增量，如下图所示。

当步长小于frame size时，相邻两帧数据之间有重叠，重叠率计算公式如下

重叠率 = (frame size – increment)/frame size *100%

当步长等于frame size时，相邻两帧数据之间无重叠，但两帧数据刚好无缝连接。

当步长大于frame size时，相邻两帧数据之间无重叠，但两帧数据之间有间隙，也就是有部分时域数据是不参与FFT计算的。

若频率分辨率为1Hz，时间步长为0.5s，则重叠率为50%，因此，实质上重叠与步长只是不同的表示方式，本质上是相同的。

如果用转速步长方式，则表示转速每变化多少截取一帧数据，如转速每变化40RPM截取一帧。按转速步长时每帧数据的重叠情况与时间步长类似，此时与转速改变速率有关。

16.稳态与跟踪

FFT分析时有两种模式：稳态和跟踪。稳态模式得到的结果为所有帧时域数据对应频谱的平均结果，且是一张二维频谱图。但跟踪模式不作平均，分别计算各帧时域数据对应的频率，将这些频谱按时间或转速先后顺序排列保存起来，每个瞬时频谱也是一张二维频谱，但如果要显示所有的频谱结果，则需要用瀑布图或colormap图来显示跟踪模式的结果。

17.自谱与互谱

自谱也称为自功率谱，本质是由频谱计算得到的，它是复数频谱乘以它的共轭。因此，自谱是实数，没有相位信息。由于它是实数，因此可以进行线性平均。由于是复数频谱与它的共轭的乘积，因此自谱有平方形式，平方形式的自谱称为自功率谱。对平方形式的自谱再求平方根，对应为线性形式，称为线性自功率谱。

线性自功率谱是最常用的，因为对于窄带信号而言，用它来表示是最合适，原因见文章《谱线是怎样影响随机信号和周期信号的PSD或自谱的？》。因此，绝大多数情况，测量的信号都是窄带信号，因此它是很多商业软件默认的谱函数形式。

互谱也是通过频谱计算得到的，但是是一个信号的频谱乘以另一个信号的频谱的共轭得到，它的结果为复数形式，有幅值和相位信息，任一频率下的相位为两个信号的相位差。因此，计算互谱时，一定是两个信号。互谱只有平方形式，因此，互谱一定是互功率谱。如果对互谱进行线性平均，两个信号不相关的成分将会被弱化。

互功率谱蕴涵两个信号之间在幅值和相位上的相互关系信息。它在任意频率处的相位值，是这两个信号在该频率的相对相位（相位差），因此，可用于研究两个信号的相位关系。另一方面，相位移动，表示的是时间移动，因此，可利用互谱检测和确定信号传递的延迟。

自谱与互谱的一个典型应用是计算频响函数FRF和相干。如进行H1估计时，用的是响应与激励的互谱除以激励的自谱，而H2估计刚好相反，用的是响应的自谱除以响应和激励的互谱。

18.自相关与互相关

自相关函数描述信号某瞬间数值与另一瞬时数值的依赖关系，由于自相关是偶函数，函数值可正可负，但在0时刻有最大值。这个最大值为信号的均方值。自相关函数是时域分析方法，它与自谱是一对傅立叶变换对。由于自相关在时间轴上是偶函数，当取时间大于0的一半来计算频谱时，得到的频谱称为半谱。自相关可用于检测混淆在无规则信号中的周期信号。

两个信号的互相关函数表示这两个信号之间一般的依赖关系，互相关函数也是一个可正可负的函数，不一定在0时刻处有最大值，也不一定是偶函数，但如果两个信号互换时，函数对称于纵轴。互相关与互谱是一对傅立叶变换对。若两个信号是两个相互独立的信号，则它们的互相关函数为零。反之，若互相关函数不等于零，则可用相关函数来表述它们的相关性。

19.相关分析与相干分析

通过上面的描述，我们已经明白相关分析是时域的分析方法，用于检测信号中的相关性。实旨上，相关分析是一种线性滤波。相关分析主要应用于以下几个方面：（1）对信号本身的分析，主要找出隐藏于不规则信号中的规律信号；（2）求两个信号之间的关系；（3）系统动态特性的测量；（4）以相关函数为基础，进行FFT变换计算自功率谱和互功率谱。

相干函数定义为输入和输出信号的互功率谱的平方除以输入信号自功率谱和输出信号自功率谱的乘积。因此，相干分析是频域的分析方式，可用于检验互功率谱和传递函数测量的有效性。

二者有一定的联系：用时域内互相关函数获得的信息，可以用频域的相干函数来获得。这是因为相干分析时用到的互功率谱函数可以由时域互相关函数得到。

20.阶次分析与阶次跟踪

阶次分析是从频域对阶次进行分析，但阶次跟踪是从阶次域对阶次进行分析。虽然二者最终的目的都是提取到想要的阶次，但又有太多的差异。阶次跟踪更偏向于对高阶次进行分析，如齿轮箱、离合器等结构。二者都需要测量转速，但阶次分析的转速是用来跟踪做频谱分析的，阶次跟踪测量转速是为了获得等角度采样数据；阶次分析是频域的，阶次跟踪是阶次域的；阶次分析是等时间采样的，阶次跟踪是等角度采样的（变采样频率）；阶次分析对于共振测量是有帮助的，但阶次跟踪却起不到这个作用；对于高阶次而言，阶次分析效果不如阶次跟踪好；阶次分析时频率分辨率固定不变，阶次跟踪时阶次分辨率固定不变；阶次跟踪不存在泄漏，无须加窗，但阶次跟踪需要加窗。

混叠

数据采集时，如果采样频率不满足采样定理，可能会导致采样后的信号存在混叠。那什么是混叠，混叠会造成什么样的误差？除了频率误差之外，还是否有其他误差？幅值正确吗？

1. 混叠定义

当采样频率设置不合理时，即采样频率低于2倍的信号频率时，会导致原本的高频信号被采样成低频信号。如下图所示，红色信号是原始的高频信号，但是由于采样频率不满足采样定理的要求，导致实际采样点如图中蓝色实心点所示，将这些蓝色实际采样点连成曲线，可以明显地看出这是一个低频信号。在图示的时间长度内，原始红色信号有18个周期，但采样后的蓝色信号只有2个周期。也就是采样后的信号频率成分为原始信号频率成分的1/9，这就是所谓的混叠：高频混叠成低频了。

对连续信号进行等时间采样时，如果采样频率不满足采样定理，采样后的信号频率就会发生混叠，即高于奈奎斯特频率（采样频率的一半）的频率成分将被重构成低于奈奎斯特频率的信号。这种频谱的重叠导致的失真称为混叠，也就是高频信号被混叠成了低频信号。

2. 混叠实例

倘若对一个正弦信号进行采样，如果采样频率等于信号频率，那么采样的时间间隔等于信号周期，因而，信号的每个周期只能采集到一个数据，如下面左图所示，将这样采样数据点连成线条，得到的线条将是一条直线，因而，对应的频率成分为0Hz。

如果采样频率为这个正弦信号的频率成分的2倍，因而，采样的时间间隔为信号周期的一半，因此，信号每个周期内的采样点数为2，也就是每个周期采集两个数据点，如上面右图所示。将这些采样点连成线条，得到的信号形状为三角波，虽然信号的频率成分没有失信，但是很难保证信号的幅值不失真。因为这两个采样点很难位于正弦信号的波峰与波谷处。也就是说，在很大程度上，采样后的信号的幅值是失真的。

通常情况下，若采样频率小于2倍的信号频率，即fs<2fa*，那么，采样后的信号将存在混叠。如下面左图所示，由于信号中存在超出奈奎斯特频率的信号存在，采样后的信号，将会使超过奈奎斯特频率成分之上的频率关于奈奎斯特频率镜像到奈奎斯特频率以下的可观测区域，如下面右图所示。

在这给出一个扫频的混叠实例。扫频信号为100-600Hz，采样频率为1000Hz，因而可观测到500Hz以内的信号成分。因此，对100-500Hz以内的信号进行采样，频率是没有问题的，但是对于超出500Hz以上的频率成分，从下面动态图中的频谱可以看出这部分信号最后混叠成了400-500Hz。

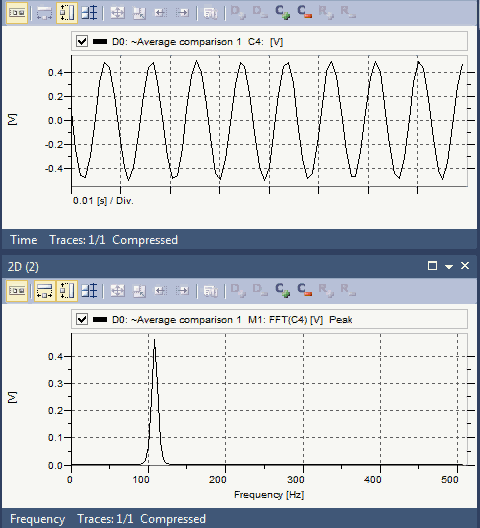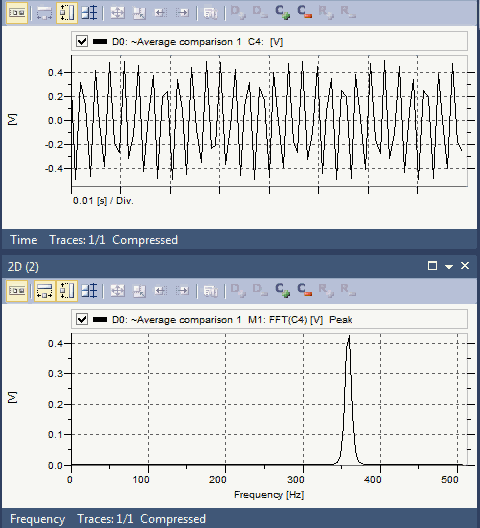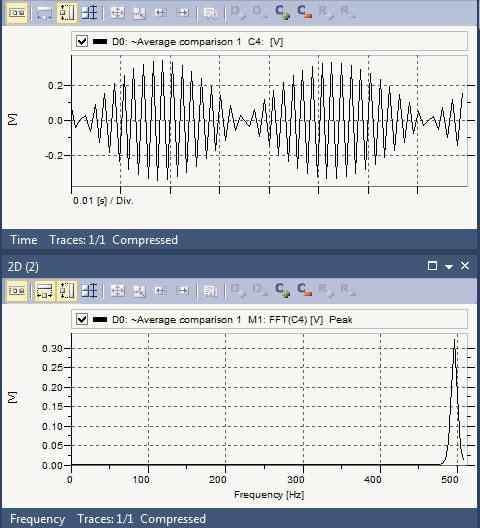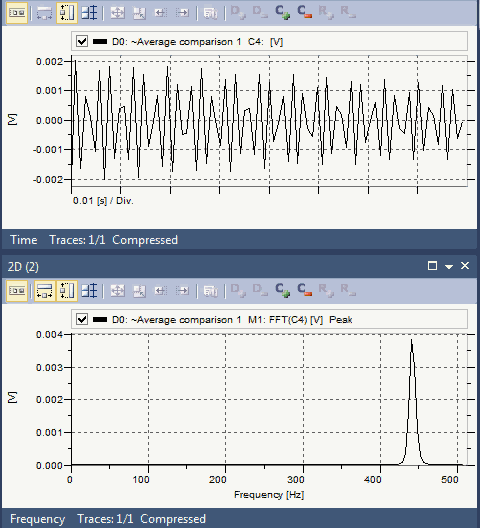
用于演示混叠现象的最经典例子之一是所谓的“车轮效应”。在影片里当马车越走越快时，马车车轮似乎越走越慢，然后甚至朝反方向运转。刚开始轮辐逆时针运转，然后逐渐变慢并开始顺时针运转。

与车轮效应相同的是转动的吊扇，小时候都见过家中的吊扇，当转速越来越快时，出现的现象是先顺时针旋转，然后静止，然后逆时针旋转。这是因为人眼在看物体时，人眼也有一定的采样速率。当人眼的采样速率跟不上越来越快的转速时，就会出现混叠现象。静止不动时的转速对应的频率就是人眼的采样速率。

人眼在观看转动的吊扇时，对于倒转现象是因为高速旋转的叶片转速非常快，在短时间内从0度顺时针旋转到330度时（假设的情况），人眼观察到的似乎是从360度逆时针旋转到330度，因此，看起来像是在倒转。

最小化混叠

既然信号可能存在混叠，怎样才能最小化混叠或者消除混叠呢？

初看起来，如果信号中没有高于奈奎斯特频率的频率成分，那么则不存在混叠。这要求采样频率极高，使得实际信号都位于奈奎斯特频率以下。但这不总是实用和可能，因为，您永远不知道真实信号的频率成分。另一个方面，虽然采样频率极高可以一定程度上避免混叠，但这样会导致出现大的数据文件，同时，最高采样频率受数据采集设备的限制。

另外，采样定理只保证了信号不被歪曲为低频信号，即使高的采样频率也不能保证不受高频信号的干扰，如果传感器输出的信号中含有比奈奎斯特频率还高的频率成分存在，ADC同样会以所选采样频率加以采样，使高于奈奎斯特频率的频率成分混入分析带宽之内。

故在采样前，应把高于奈奎斯特频率成分以上的频率滤掉，这就需要抗混叠滤波器，它是一个低通滤波器：低于奈奎斯特频率的频率通过，移除高于奈奎斯特频率的频率成分，这是理想的滤波器。

实际情况是任何滤波器都不是理想的滤波器，抗混叠滤波器也不例外。滤波器存在滤波陡度，在滤波截止频率（奈奎斯特频率）以上的一些区域还存在混叠的可能性，这个区域对应带宽的80%以上部分，也就是带宽的80%-100%区域。如下图所示，高于奈奎斯特频率以上的频率成分会关于奈奎斯特频率镜像到带宽的80%-100%区域，形成混叠，而带宽80%以内的区域，是无混叠的。

当然了，如果信号中没有高于奈奎斯特频率的成分存在，则整个带宽都不存在混叠。当信号还有高于奈奎斯特频率有成分存在时，按采样定理设置采样频率时，带宽的80%以上频带则存在混叠，如下图红框所示区域即遭受了频率混叠的影响。由于带宽以上还有信号存在，因此，这些频率关于带宽镜像到了带宽以内。

通过这一部分的分析可知，即使使用抗混叠滤波器，在带宽的80%以上的频率区间还可能存在混叠，如要整个频带都无混叠，则采样频率至少高于信号频率的2.5倍以上。

计算混叠后的频率

若没有抗混叠滤波器存在，信号必然存在混叠，那么怎么求解混叠后的频率成分？在这介绍两种方法：一种称为镜像法，一种称为公式法。

镜像法

假设信号的频率fa大于采样频率fs，因此，采样后必然存在混叠。这时，信号频率将会关于离它最近的整数倍的奈奎斯特频率镜像，如果镜像后的频率位于观测的带宽以内，则是混叠后的频率。如果镜像后的频率还未位于观测的带宽以内，则会关于下一个整数倍的奈奎斯特频率镜像（往0Hz方向），直到镜像到带宽以内为止。

如下图所示，信号的频率fa首先关于3倍奈奎斯特频率镜像，但此时还不是带宽以内，所以，之前镜像后的频率又关于2倍奈奎斯特频率镜像，但还不是带宽以内，需要继续将关于2倍奈奎斯特频率镜像后的频率关于1倍奈奎斯特频率镜像，这时，频率终于位于观测的带宽以内，这就是混叠后的频率fd。

公式法

对于混叠现象，也可以从下面的数学公式得到混叠后的频率

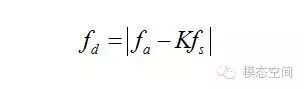
K是个整数，取值从0开始，适当的取值应使得|fa-Kfs|最小。因而，可以将上式写成

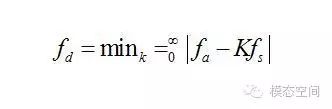
比如考虑采样频率为500Hz，采集各种不同频率的信号，结果如下表所示，注意数字化后的频率重复出现。

实际频率fa Hz	最小K值	混叠的频率fd Hz
180	0	180
280	1	220
380	1	120
480	1	20
580	1	80
680	1	180
780	2	220
880	2	120
980	2	20

5. 阶次混叠

除了频率混叠之外，还会存在阶次混叠。由于阶次可以在频域显示也可以在阶次域显示，因此，阶次混叠存在频域混叠和阶次域混叠两种情况。

在频域显示时，阶次是斜线，高于最大阶次以上的阶次成分会关于最大阶次线镜像到最大阶次以内，如下面左图所示。当在阶次域时，阶次垂直于横纵，此时阶次混叠类似于频率混叠，如下面右图所示。

下图中，左图为60个PPR采集得到的信号，那么，能分析到的最大阶次为30阶次。信号的主要阶次为1，2，10，17阶次。右图为20个PPR采集得到的信号，那么，能分析的最大阶次为10阶次。此时，右图中的主要阶次为1，2，3，10阶次。右图中没有17阶次，多出来一个3阶次。这是由于采用20个PPR进行信号采集时，只能采集得到10阶次以内的信息，17阶次高于最大阶次，此时，17阶次将关于最大阶次线混叠成了3阶次（17阶次关于10阶次镜像成了3阶次），这是阶次混叠现象。

机械振动信号，时频域特征提取

''' ============== 特征提取的类 =====================
时域特征 ：11类
频域特征 : 13类
总共提取特征 ： 24类

参考文献 英文文献 016_C_(Q1 时域和频域共24种特征参数 )  Fault diagnosis of rotating machinery based on multiple ANFIS combination with GAs

'''

import numpy as np

import scipy.stats
import matplotlib.pyplot as plt

class Fea_Extra():
    def __init__(self, Signal, Fs = 25600):
        self.signal = Signal
        self.Fs = Fs

    def Time_fea(self, signal_):
        """
        提取时域特征 11 类
        """
        N = len(signal_)
        y = signal_
        t_mean_1 = np.mean(y)                                    # 1_均值（平均幅值）

        t_std_2  = np.std(y, ddof=1)                             # 2_标准差

        t_fgf_3  = ((np.mean(np.sqrt(np.abs(y)))))**2           # 3_方根幅值

        t_rms_4  = np.sqrt((np.mean(y**2)))                      # 4_RMS均方根

        t_pp_5   = 0.5*(np.max(y)-np.min(y))                     # 5_峰峰值  (参考周宏锑师姐 博士毕业论文)

        #t_skew_6   = np.sum((t_mean_1)**3)/((N-1)*(t_std_3)**3)
        t_skew_6   = scipy.stats.skew(y)                         # 6_偏度 skewness

        #t_kur_7   = np.sum((y-t_mean_1)**4)/((N-1)*(t_std_3)**4)
        t_kur_7 = scipy.stats.kurtosis(y)                        # 7_峭度 Kurtosis

        t_cres_8  = np.max(np.abs(y))/t_rms_4                    # 8_峰值因子 Crest Factor

        t_clear_9  = np.max(np.abs(y))/t_fgf_3                   # 9_裕度因子  Clearance Factor

        t_shape_10 = (N * t_rms_4)/(np.sum(np.abs(y)))           # 10_波形因子 Shape fator

        t_imp_11  = ( np.max(np.abs(y)))/(np.mean(np.abs(y)))  # 11_脉冲指数 Impulse Fator

        t_fea = np.array([t_mean_1, t_std_2, t_fgf_3, t_rms_4, t_pp_5,
                          t_skew_6,   t_kur_7,  t_cres_8,  t_clear_9, t_shape_10, t_imp_11 ])

        #print("t_fea:",t_fea.shape,'\n', t_fea)
        return t_fea

    def Fre_fea(self, signal_):
        """
        提取频域特征 13类
        :param signal_:
        :return:
        """
        L = len(signal_)
        PL = abs(np.fft.fft(signal_ / L))[: int(L / 2)]
        PL[0] = 0
        f = np.fft.fftfreq(L, 1 / self.Fs)[: int(L / 2)]
        x = f
        y = PL
        K = len(y)
        # print("signal_.shape:",signal_.shape)
        # print("PL.shape:", PL.shape)
        # print("L:", L)
        # print("K:", K)
        # print("x:",x)
        # print("y:",y)

        f_12 = np.mean(y)

        f_13 = np.var(y)

        f_14 = (np.sum((y - f_12)**3))/(K * ((np.sqrt(f_13))**3))

        f_15 = (np.sum((y - f_12)**4))/(K * ((f_13)**2))

        f_16 = (np.sum(x * y))/(np.sum(y))

        f_17 = np.sqrt((np.mean(((x- f_16)**2)*(y))))

        f_18 = np.sqrt((np.sum((x**2)*y))/(np.sum(y)))

        f_19 = np.sqrt((np.sum((x**4)*y))/(np.sum((x**2)*y)))

        f_20 = (np.sum((x**2)*y))/(np.sqrt((np.sum(y))*(np.sum((x**4)*y))))

        f_21 = f_17/f_16

        f_22 = (np.sum(((x - f_16)**3)*y))/(K * (f_17**3))

        f_23 = (np.sum(((x - f_16)**4)*y))/(K * (f_17**4))

        #f_24 = (np.sum((np.sqrt(x - f_16))*y))/(K * np.sqrt(f_17))    # f_24的根号下出现负号，无法计算先去掉


        #print("f_16:",f_16)

        #f_fea = np.array([f_12, f_13, f_14, f_15, f_16, f_17, f_18, f_19, f_20, f_21, f_22, f_23, f_24])
        f_fea = np.array([f_12, f_13, f_14, f_15, f_16, f_17, f_18, f_19, f_20, f_21, f_22, f_23])

        #print("f_fea:",f_fea.shape,'\n', f_fea)
        return f_fea

    def Both_Fea(self):
        """
        :return: 时域、频域特征 array
        """
        t_fea = self.Time_fea(self.signal)
        f_fea = self.Fre_fea(self.signal)
        fea = np.append(np.array(t_fea), np.array(f_fea))
        #print("fea:", fea.shape, '\n', fea)
        return fea

时频域统计特征

振动信号原始统计特征分为两类：时域统计特征、频域统计特征。

信号的时域特征是通过统计分析信号的各种时域参数、指标的估计或计算得到的，如表所示，分为有量纲参数和无量纲参数两种，其中1-9为有量纲参数和10-15无量纲参数。

def get_time_domain_features(data):
    '''data为一维振动信号'''
    x_rms = 0
    absXbar = 0
    x_r = 0
    S = 0
    K = 0
    k = 0
    x_rms = 0
    fea = []
    len_ = len(data.iloc[0, :])
    mean_ = data.mean(axis=1)  # 1.均值
    var_ = data.var(axis=1)  # 2.方差
    std_ = data.std(axis=1)  # 3.标准差
    max_ = data.max(axis=1)  # 4.最大值
    min_ = data.min(axis=1)  # 5.最小值
    x_p = max(abs(max_[0]), abs(min_[0]))  # 6.峰值
    for i in range(len_):
        x_rms += data.iloc[0, i] ** 2
        absXbar += abs(data.iloc[0, i])
        x_r += math.sqrt(abs(data.iloc[0, i]))
        S += (data.iloc[0, i] - mean_[0]) ** 3
        K += (data.iloc[0, i] - mean_[0]) ** 4
    x_rms = math.sqrt(x_rms / len_)  # 7.均方根值
    absXbar = absXbar / len_  # 8.绝对平均值
    x_r = (x_r / len_) ** 2  # 9.方根幅值
    W = x_rms / mean_[0]  # 10.波形指标
    C = x_p / x_rms  # 11.峰值指标
    I = x_p / mean_[0]  # 12.脉冲指标
    L = x_p / x_r  # 13.裕度指标
    S = S / ((len_ - 1) * std_[0] ** 3)  # 14.偏斜度
    K = K / ((len_ - 1) * std_[0] ** 4)  # 15.峭度

    fea = [mean_[0],absXbar,var_[0],std_[0],x_r,x_rms,x_p,max_[0],min_[0],W,C,I,L,S,K]
    return fea

小波包

傅里叶变换

做完FFT（快速傅里叶变换）后，可以在频谱上看到清晰的四条线，信号包含四个频率成分。

如上图，最上边的是频率始终不变的平稳信号。而下边两个则是频率随着时间改变的非平稳信号，它们同样包含和最上信号相同频率的四个成分。
做FFT后，我们发现这三个时域上有巨大差异的信号，频谱（幅值谱）却非常一致。尤其是下边两个非平稳信号，我们从频谱上无法区分它们，因为它们包含的四个频率的信号的成分确实是一样的，只是出现的先后顺序不同。

可见，傅里叶变换处理非平稳信号有天生缺陷。它只能获取一段信号总体上包含哪些频率的成分，但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号，可能频谱图一样。

然而平稳信号大多是人为制造出来的，自然界的大量信号几乎都是非平稳的，所以在比如生物医学信号分析等领域的论文中，基本看不到单纯傅里叶变换这样naive的方法。

上图所示的是一个正常人的事件相关电位。对于这样的非平稳信号，只知道包含哪些频率成分是不够的，我们还想知道各个成分出现的时间。知道信号频率随时间变化的情况，各个时刻的瞬时频率及其幅值——这也就是时频分析。

短时傅里叶变换(STFT)

一个简单可行的方法就是——加窗。我又要套用方沁园同学的描述了，“把整个时域过程分解成无数个等长的小过程，每个小过程近似平稳，再傅里叶变换，就知道在哪个时间点上出现了什么频率了。”这就是短时傅里叶变换。

时域上分成一段一段做FFT，不就知道频率成分随着时间的变化情况了吗！

用这样的方法，可以得到一个信号的时频图了：

图上既能看到10Hz, 25 Hz, 50 Hz, 100 Hz四个频域成分，还能看到出现的时间。两排峰是对称的，所以大家只用看一排就行了。

是不是棒棒的？时频分析结果到手。但是STFT依然有缺陷。

使用STFT存在一个问题，我们应该用多宽的窗函数？

窗太宽太窄都有问题：

窗太窄，窗内的信号太短，会导致频率分析不够精准，频率分辨率差。窗太宽，时域上又不够精细，时间分辨率低。
（这里插一句，这个道理可以用海森堡不确定性原理来解释。类似于我们不能同时获取一个粒子的动量和位置，我们也不能同时获取信号绝对精准的时刻和频率。这也是一对不可兼得的矛盾体。我们不知道在某个瞬间哪个频率分量存在，我们知道的只能是在一个时间段内某个频带的分量存在。 所以绝对意义的瞬时频率是不存在的。）

上图对同一个信号（4个频率成分）采用不同宽度的窗做STFT，结果如右图。用窄窗，时频图在时间轴上分辨率很高，几个峰基本成矩形，而用宽窗则变成了绵延的矮山。但是频率轴上，窄窗明显不如下边两个宽窗精确。

所以窄窗口时间分辨率高、频率分辨率低，宽窗口时间分辨率低、频率分辨率高。对于时变的非稳态信号，高频适合小窗口，低频适合大窗口。然而STFT的窗口是固定的，在一次STFT中宽度不会变化，所以STFT还是无法满足非稳态信号变化的频率的需求。

小波变换

那么你可能会想到，让窗口大小变起来，多做几次STFT不就可以了吗？！没错，小波变换就有着这样的思路。
但事实上小波并不是这么做的（关于这一点，方沁园同学的表述“小波变换就是根据算法，加不等长的窗，对每一小部分进行傅里叶变换”就不准确了。小波变换并没有采用窗的思想，更没有做傅里叶变换。）
至于为什么不采用可变窗的STFT呢，我认为是因为这样做冗余会太严重，STFT做不到正交化，这也是它的一大缺陷。

于是小波变换的出发点和STFT还是不同的。STFT是给信号加窗，分段做FFT；而小波直接把傅里叶变换的基给换了——将无限长的三角函数基换成了有限长的会衰减的小波基。这样不仅能够获取频率，还可以定位到时间了~

这个基函数会伸缩、会平移（其实本质并非平移，而是两个正交基的分解）。缩得窄，对应高频；伸得宽，对应低频。然后这个基函数不断和信号做相乘。某一个尺度（宽窄）下乘出来的结果，就可以理解成信号所包含的当前尺度对应频率成分有多少。于是，基函数会在某些尺度下，与信号相乘得到一个很大的值，因为此时二者有一种重合关系。那么我们就知道信号包含该频率的成分的多少。

仔细体会可以发现，这一步其实是在计算信号和三角函数的相关性。

看，这两种尺度能乘出一个大的值（相关度高），所以信号包含较多的这两个频率成分，在频谱上这两个频率会出现两个峰。

以上，就是粗浅意义上傅里叶变换的原理。

如前边所说，小波做的改变就在于，将无限长的三角函数基换成了有限长的会衰减的小波基。

这就是为什么它叫“小波”，因为是很小的一个波嘛~

从公式可以看出，不同于傅里叶变换，变量只有频率ω，小波变换有两个变量：尺度a（scale）和平移量 τ（translation）。尺度a控制小波函数的伸缩，平移量 τ控制小波函数的平移。尺度就对应于频率（反比），平移量 τ就对应于时间。

当伸缩、平移到这么一种重合情况时，也会相乘得到一个大的值。这时候和傅里叶变换不同的是，这不仅可以知道信号有这样频率的成分，而且知道它在时域上存在的具体位置。

而当我们在每个尺度下都平移着和信号乘过一遍后，我们就知道信号在每个位置都包含哪些频率成分。

看到了吗？有了小波，我们从此再也不害怕非稳定信号啦！从此可以做时频分析啦！

做傅里叶变换只能得到一个频谱，做小波变换却可以得到一个时频谱！

小波包分解

小波包是为了克服小波分解在高频段的频率分辨率较差，而在低频段的时间分辨率较差的问题的基础上而提出的。

它是一种更精细的信号分析的方法，提高了信号的时域分辨率。

下面是两者的对比图：

*能量谱*

给出两部分代码，写成两个函数。一个是小波包分解与重构，另一个是能量谱函数。

下载地址：https://download.csdn.net/download/ckzhb/10030651

代码名称：wavelet_packetdecomposition_reconstruct

function wpt= wavelet_packetdecomposition_reconstruct( x,n,wpname )
%% 对信号进行小波包分解，得到节点的小波包系数。然后对每个节点系数进行重构。 
% Decompose x at depth n with wpname wavelet packets.using Shannon entropy.
%   
%  x-input signal,列向量。
%  n-the number of decomposition layers
%  wpname-a particular wavelet.type:string.
%
%Author hubery_zhang
%Date 20170714

%%
wpt=wpdec(x,n,wpname);
% Plot wavelet packet tree (binary tree)
plot(wpt)
%% wavelet packet coefficients.default：use the front 4.
cfs0=wpcoef(wpt,[n 0]);
cfs1=wpcoef(wpt,[n 1]);
cfs2=wpcoef(wpt,[n 2]);
cfs3=wpcoef(wpt,[n 3]);
figure;
subplot(5,1,1);
plot(x);
title('原始信号');
subplot(5,1,2);
plot(cfs0);
title(['结点 ',num2str(n) '  1',' 系数'])
subplot(5,1,3);
plot(cfs1);
title(['结点 ',num2str(n) '  2',' 系数'])
subplot(5,1,4);
plot(cfs2);
title(['结点 ',num2str(n) '  3',' 系数'])
subplot(5,1,5);
plot(cfs3);
title(['结点 ',num2str(n) '  4',' 系数'])
%% reconstruct wavelet packet coefficients.
rex0=wprcoef(wpt,[n 0]);
rex1=wprcoef(wpt,[n 1]);
rex2=wprcoef(wpt,[n 2]);
rex3=wprcoef(wpt,[n 3]);
figure;
subplot(5,1,1);
plot(x);
title('原始信号');
subplot(5,1,2);
plot(rex0);
title(['重构结点 ',num2str(n) '  1',' 系数'])
subplot(5,1,3);
plot(rex1);
title(['重构结点 ',num2str(n) '  2',' 系数'])
subplot(5,1,4);
plot(rex2);
title(['重构结点 ',num2str(n) '  3',' 系数'])
subplot(5,1,5);
plot(rex3);
title(['重构结点 ',num2str(n) '  4',' 系数'])
end

代码名称：wavelet_energy_spectrum

function E = wavelet_energy_spectrum( wpt,n )
%% 计算每一层每一个节点的能量
%  wpt-wavelet packet tree
%  n-第n层能量
% 
% Author hubery_zhang
% Date  20170714

%%
% 求第n层第i个节点的系数
E(1:2^n )=0;
for i=1:2^n 
E(i) = norm(wpcoef(wpt,[n,i-1]),2)^2; %20180604更新 原代码：E(i) = norm(wpcoef(wpt,[n,i-1]),2)
end
%求每个节点的概率
E_total=sum(E); 
for i=1:2^n
p_node(i)= 100*E(i)/E_total;
end
% E = wenergy(wpt); only get the last layer
figure;
x=1:2^n;
bar(x,p_node);
title(['第',num2str(n),'层']);
axis([0 2^n 0 100]);
xlabel('结点');
ylabel('能量百分比/%');
for j=1:2^n
text(x(j),p_node(i),num2str(p_node(j),'%0.2f'),...
    'HorizontalAlignment','center',...
    'VerticalAlignment','bottom')
end

end

EMD和类EMD方法

1. EEMD (Ensemble Empirical Mode Decomposition) EEMD是EMD的一种改进算法，可以通过增加噪声，使得分解结果更加稳定，鲁棒性更强。但是，EEMD会产生大量的模态成分，导致计算成本较高，同时，噪声的添加也可能会影响分解结果的精度。
2. CEEMD (Complete Ensemble Empirical Mode Decomposition with Adaptive Noise) CEEMD是对EEMD的进一步改进，它采用了自适应噪声策略，不需要手动设置噪声，能够有效地避免噪声影响，并提高了分解的准确性。但是，同样由于大量的模态成分，计算成本也比较高。
3. CEEMDAN (Complete Ensemble Empirical Mode Decomposition with Adaptive Noise and AM-FM Components) CEEMDAN是对CEEMD的扩展，引入了AM-FM（包络-调制）变换，以进一步提高信号分解的效果。但是，同样会产生大量的模态成分，计算成本较高。
4. VMD (Variational Mode Decomposition) VMD是一种全局优化的信号分解方法。它是基于能量函数的变分原理，在极小化该能量函数的过程中，得到一系列数学模态函数。VMD具有良好的分解性能和计算效率，但对于噪声的鲁棒性较差。
5. ICEEMDAN (Intrinsic Complete Ensemble Empirical Mode Decomposition with Adaptive Noise) ICEEMDAN是对CEEMDAN的改进，它使用了内部迭代的方法，在分解过程中获得更好的精度。但是，ICEEMDAN也会产生大量的模态成分，计算成本较高。
6. LMD (Local Mean Decomposition) LMD是一种局部平均分解方法，它通过对信号进行局部平均，得到一系列信号分量。LMD对于非线性和非平稳信号处理效果较好，但需要选择合适的窗口大小。
7. EWT (Empirical Wavelet Transform) EWT是一种基于小波的信号分解方法，它将小波分解中的预定义小波函数替换为自适应信号分量。EWT对信号分解的精度和计算效率都有很好的表现，特别是在非平稳信号的情况下。

如果希望得到更好的鲁棒性和准确性，可以考虑使用CEEMDAN或ICEEMDAN方法；如果要求计算效率较高，可以选择VMD或EWT方法。

VMD和能量熵的信号分析

由于传统的EMD分解容易方法容易出现模态混叠和端点效应的问题，提出用VMD的分解方法来对电机轴承故障进行研究。VMD模态分解数量K值必须人为设定，为了避免人为设置参数的影响，提出PSO优化VMD的方法来确定最佳的模态分解数量K和惩罚因子的参数，并且和传统EMD分解的MF进行时域和频域的对比，以仿真信号和电机轴承故障实验数据信号作为研究对象，进行EMD和VMD的分解。最后结合小波包能量熵理论提出了一种基于VMD能量熵的量化分析方法，利用VMD得到其相对能量特征分布，通过计算相应熵值，对电机轴承不同磨损在不同工况下进行量化分析。

短时Fourier

) VMD是一种全局优化的信号分解方法。它是基于能量函数的变分原理，在极小化该能量函数的过程中，得到一系列数学模态函数。VMD具有良好的分解性能和计算效率，但对于噪声的鲁棒性较差。
5. ICEEMDAN (Intrinsic Complete Ensemble Empirical Mode Decomposition with Adaptive Noise) ICEEMDAN是对CEEMDAN的改进，它使用了内部迭代的方法，在分解过程中获得更好的精度。但是，ICEEMDAN也会产生大量的模态成分，计算成本较高。
6. LMD (Local Mean Decomposition) LMD是一种局部平均分解方法，它通过对信号进行局部平均，得到一系列信号分量。LMD对于非线性和非平稳信号处理效果较好，但需要选择合适的窗口大小。
7. EWT (Empirical Wavelet Transform) EWT是一种基于小波的信号分解方法，它将小波分解中的预定义小波函数替换为自适应信号分量。EWT对信号分解的精度和计算效率都有很好的表现，特别是在非平稳信号的情况下。

如果希望得到更好的鲁棒性和准确性，可以考虑使用CEEMDAN或ICEEMDAN方法；如果要求计算效率较高，可以选择VMD或EWT方法。

VMD和能量熵的信号分析

由于传统的EMD分解容易方法容易出现模态混叠和端点效应的问题，提出用VMD的分解方法来对电机轴承故障进行研究。VMD模态分解数量K值必须人为设定，为了避免人为设置参数的影响，提出PSO优化VMD的方法来确定最佳的模态分解数量K和惩罚因子的参数，并且和传统EMD分解的MF进行时域和频域的对比，以仿真信号和电机轴承故障实验数据信号作为研究对象，进行EMD和VMD的分解。最后结合小波包能量熵理论提出了一种基于VMD能量熵的量化分析方法，利用VMD得到其相对能量特征分布，通过计算相应熵值，对电机轴承不同磨损在不同工况下进行量化分析。

短时Fourier

经典Fourier变换只能反映信号的整体特性(完全是时域或者频域)。要求信号满足平稳条件