目录
Dijkstra算法

原理讲解
首先介绍广度优先搜索算法(Breadth First Search,BFS):从出发点依次访问各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得“先被访问节点的邻接点先于后被访问的节点的邻接点”被访问。
什么意思?
以下图为例,从图中节点1出发,依次访问它附近的邻接节点2和8,再去依次访问节点2附近的邻接节点3和5,然后访问节点8下的节点6和节点9,最后再访问节点4和节点7。这就叫广度优先搜索。

Dijkstra算法属于典型的广度优先搜索算法(Breadth First Search,BFS)。
这个【例子】可以直观的告诉我们什么是Dijkstra算法:如下拓扑结构图所示,D点为起点,A点为终点,利用Dijkstra算法获取由D到A的最短路径。

【分析】
将“离起始位置距离最短的”节点存入集合,比如说起点
与自身的距离最短为0,我们就将
存放进集合
,此时
.

将“拓扑结构图中其他未确定离起始点距离和未求解出路径的”节点存入集合,未知的距离用
表示,则有
.
然后我们发现在集合中
点距离起始
点最短,那么把
点从集合
移入集合
,此时
.
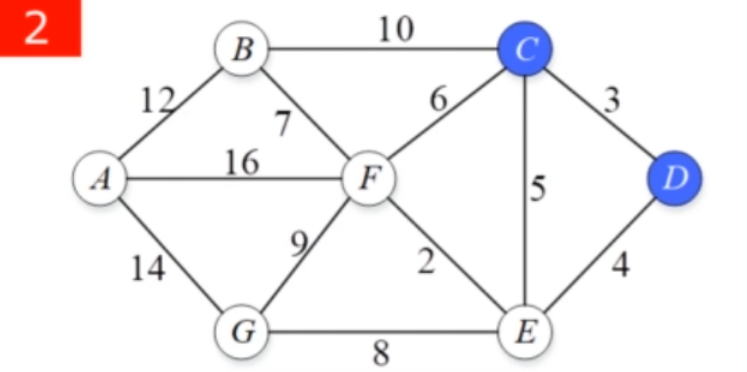
由于点的确定,集合
中
点的邻接点到起始
点的距离发生了更新,即
点到
点的距离更新为
,记为
;
点到
点的距离更新为
,记为
;由于
点到
点的距离原来是4,经过C点变为了
,保留最短距离,故仍然是
。综上,此时的集合
为
.
发现此时集合中的
点距离起始
点最短,把
点从集合
移入集合
,此时
.

同样的由于点的确定,邻接点
和邻接点
的距离数据发生了更新,
点到
点距离更新为
,
点到
点距离更新为
,即
.
发现此时集合中的
点距离起始
点最短,把
点从集合
移入集合
,此时
.

集合内各节点距离数据发生了更新
此时我们发现已经找到一条通往点的路径,我们先记住这条路径和距离(代价)
,距离为
.
接着同样的依次将点和
点移入集合
,同样可以得到通往
点的路径
和
,距离(代价)分别为
和
,由此我们就能得到最短一条路径为
。

代码实现
我们通过Matlab来进行Dijkstra算法的仿真
准备目录结构:

利用Matlab绘制一个栅格地图,并封装为defColorMap函数:
function [field,cmap] = defColorMap(rows, cols)
cmap = [1 1 1; ... % 1-白色-空地
0 0 0; ... % 2-黑色-静态障碍
1 0 0; ... % 3-红色-动态障碍
1 1 0;... % 4-黄色-起始点
1 0 1;... % 5-紫色-目标点
0 1 0; ... % 6-绿色-到目标点的规划路径
0 1 1]; % 7-青色-动态规划的路径
% 构建颜色MAP图
colormap(cmap);
% 定义栅格地图全域,并初始化空白区域
field = ones(rows, cols);
% 障碍物区域
obsRate = 0.3;
obsNum = floor(rows*cols*obsRate);
obsIndex = randi([1,rows*cols],obsNum,1);
field(obsIndex) = 2;
Dijkstra.m用于初始化算法:
% Dijkstra算法
clc
clear
close all
%% 栅格界面、场景定义
% 行数和列数
rows = 10;
cols = 20;
[field,cmap] = defColorMap(rows, cols);
% 起点、终点、障碍物区域
startPos = 2;
goalPos = rows*cols-2;
field(startPos) = 4;
field(goalPos) = 5;
%% 算法初始化
% S/U的第一列表示栅格节点线性索引编号
% 对于S,第二列表示从源节点到本节点已求得的最小距离,不再变更;
% 对于U,第二列表示从源节点到本节点暂时求得的最小距离,可能会变更
U(:,1) = (1: rows*cols)';
U(:,2) = inf;
S = [startPos, 0];
U(startPos,:) = [];
% 更新起点的邻节点及代价
neighborNodes = getNeighborNodes(rows, cols, startPos, field);
for i = 1:8
childNode = neighborNodes(i,1);
% 判断该子节点是否存在
if ~isinf(childNode)
idx = find(U(:,1) == childNode);
U(idx,2) = neighborNodes(i,2);
end
end
% S集合的最优路径集合
for i = 1:rows*cols
path{i,1} = i;
end
for i = 1:8
childNode = neighborNodes(i,1);
if ~isinf(neighborNodes(i,2))
path{childNode,2} = [startPos,neighborNodes(i,1)];
end
end
%% 循环遍历
while ~isempty(U)
% 在U集合找出当前最小距离值的节点,视为父节点,并移除该节点至S集合中
[dist_min, idx] = min(U(:,2));
parentNode = U(idx, 1);
S(end+1,:) = [parentNode, dist_min];
U(idx,:) = [];
% 获得当前节点的临近子节点
neighborNodes = getNeighborNodes(rows, cols, parentNode, field);
% 依次遍历邻近子节点,判断是否在U集合中更新邻节点的距离值
for i = 1:8
% 需要判断的子节点
childNode = neighborNodes(i,1);
cost = neighborNodes(i,2);
if ~isinf(childNode) && ~ismember(childNode, S)
% 找出U集合中节点childNode的索引值
idx_U = find(childNode == U(:,1));
% 判断是否更新
if dist_min + cost < U(idx_U, 2)
U(idx_U, 2) = dist_min + cost;
% 更新最优路径
path{childNode, 2} = [path{parentNode, 2}, childNode];
end
end
end
end
%% 画栅格界面
% 找出目标最优路径
path_opt = path{goalPos,2};
field(path_opt(2:end-1)) = 6;
% 画栅格图
image(1.5,1.5,field);
grid on;
set(gca,'gridline','-','gridcolor','k','linewidth',2,'GridAlpha',0.5);
set(gca,'xtick',1:cols+1,'ytick',1:rows+1);
axis image;getNeighborNodes.m是用于获得邻接点信息的函数:
function neighborNodes = getNeighborNodes(rows, cols, lineIndex, field)
[row, col] = ind2sub([rows,cols], lineIndex);
neighborNodes = inf(8,2);
%% 查找当前父节点临近的周围8个子节点
% 左上节点
if row-1 > 0 && col-1 > 0
child_node_sub = [row-1, col-1];
child_node_line = sub2ind([rows,cols], child_node_sub(1), child_node_sub(2));
neighborNodes(1,1) = child_node_line;
if field(child_node_sub(1), child_node_sub(2)) ~= 2
cost = norm(child_node_sub - [row, col]);
neighborNodes(1,2) = cost;
end
end
% 上节点
if row-1 > 0
child_node_sub = [row-1, col];
child_node_line = sub2ind([rows,cols], child_node_sub(1), child_node_sub(2));
neighborNodes(2,1) = child_node_line;
if field(child_node_sub(1), child_node_sub(2)) ~= 2
cost = norm(child_node_sub - [row, col]);
neighborNodes(2,2) = cost;
end
end
% 右上节点
if row-1 > 0 && col+1 <= cols
child_node_sub = [row-1, col+1];
child_node_line = sub2ind([rows,cols], child_node_sub(1), child_node_sub(2));
neighborNodes(3,1) = child_node_line;
if field(child_node_sub(1), child_node_sub(2)) ~= 2
cost = norm(child_node_sub - [row, col]);
neighborNodes(3,2) = cost;
end
end
% 左节点
if col-1 > 0
child_node_sub = [row, col-1];
child_node_line = sub2ind([rows,cols], child_node_sub(1), child_node_sub(2));
neighborNodes(4,1) = child_node_line;
if field(child_node_sub(1), child_node_sub(2)) ~= 2
cost = norm(child_node_sub - [row, col]);
neighborNodes(4,2) = cost;
end
end
% 右节点
if col+1 <= cols
child_node_sub = [row, col+1];
child_node_line = sub2ind([rows,cols], child_node_sub(1), child_node_sub(2));
neighborNodes(5,1) = child_node_line;
if field(child_node_sub(1), child_node_sub(2)) ~= 2
cost = norm(child_node_sub - [row, col]);
neighborNodes(5,2) = cost;
end
end
% 左下节点
if row+1 <= rows && col-1 > 0
child_node_sub = [row+1, col-1];
child_node_line = sub2ind([rows,cols], child_node_sub(1), child_node_sub(2));
neighborNodes(6,1) = child_node_line;
if field(child_node_sub(1), child_node_sub(2)) ~= 2
cost = norm(child_node_sub - [row, col]);
neighborNodes(6,2) = cost;
end
end
% 7.下节点
if row+1 <= rows
child_node_sub = [row+1, col];
child_node_line = sub2ind([rows,cols], child_node_sub(1), child_node_sub(2));
neighborNodes(7,1) = child_node_line;
if field(child_node_sub(1), child_node_sub(2)) ~= 2
cost = norm(child_node_sub - [row, col]);
neighborNodes(7,2) = cost;
end
end
% 8.右下节点
if row+1 <= rows && col+1 <= cols
child_node_sub = [row+1, col+1];
child_node_line = sub2ind([rows,cols], child_node_sub(1), child_node_sub(2));
neighborNodes(8,1) = child_node_line;
if field(child_node_sub(1), child_node_sub(2)) ~= 2
cost = norm(child_node_sub - [row, col]);
neighborNodes(8,2) = cost;
end
end
最后运行Dijkstra.m程序即可。

制作不易,对您有帮助的话就点赞收藏支持一下,感谢感谢~
























 6161
6161

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










