贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础。朴素贝叶斯分类就是其中一种,之所以称为朴素, 是因为其思想很简单,且建立在两个看似鲁莽的假设之上。朴素贝叶斯认为,概率最大的那个类,就是待分类对象的所属类,且假设(1)所有特征属性统计独立;(2)所有特征属性同等重要,权重相同。这两个看似鲁莽的假设,在很多实际应用中却有很好的效果,因此朴素贝叶斯分类器任然被广泛使用。
一、理论基础
想必大家都应该很熟悉贝叶斯定理:
通过该定理,我们可以从P(A|B)求得P(B|A),而往往P(A|B)是比较容易直接求出的,P(B|A)却很难直接得到,这就是这个定理的价值所在。将这个定理用到分类问题中,可以重写为:
其中Ci表示第i个类别,w表示一组特征属性,即 w = { a1, a2, a3, ......}。上式可以这样解释:
在实际使用中,w出现的概率即P(w)一般不考虑,因为其对所有类别都是相等的,要比较概率的大小,只需比较上式中的分子即可。
现在的问题就是,如何求得分子中的两项。
我们知道w是一组特征属性,我们将其展开写为下式:
还记得朴素贝叶斯的两个假设吗,所有特征属性统计独立且权重相同,由此我们可以得到:
因此,我们只需在训练时,统计每一个类别中每一个特征属性的频率,然后将他们乘起来即可。
对于p(ci)的求取,很是简单,只需统计训练样本中ci类别出现的频率即可。
实际上,以上方法是不完整的,只对特征属性都是二值分布(取值只有0和1)时适用,即只适用于离散情况下的分类。完整的,我们应该将p( aj | ci )看做一个概率分布,而不仅仅只是一个概率,这样,当特征属性是连续值时,应该通过概率分布来求得当前属性值所对应的概率。一般的,我们假设连续特征属性的概率分布为正态分布,也即高斯分布:
这样在训练时,可以通过一组aj求得其平均值和方差,从而得到高斯分布。当然,高斯分布只针对一般情况,特征属性的概率分布也可以满足其他任意一种分布。
一句话,朴素贝叶斯的训练过程,就是求取特征属性概率分布的过程。
二、代码实现
在编写代码之前,先要做一些细节上的处理。首先,我们要计算多个概率的乘积,而概率的值往往都较小,相乘之后可能会underflow,变成0,得到错误的结果。因此我们对乘式两边取自然对数,将乘法转换为加法:
别忘了最后还要加上p(ci)的对数。由于取对数不会改变原来乘式的单调性,因此可以直接用相加后的结果进行比较,对数大的,概率也大。
其次,在进行离散情况下的分类时,我们使用频率来代替概率,因此有可能出现概率为0的情况,如果将0概率带入计算,结果必然是零。为了解决这一问题,我们引入Laplace校准,具体方法很简单,就是对每一特征属性的计数都加1,这样即使该属性没有出现过一次,也有一个较小的概率,且当训练样本较大时,这一修改不会造成什么影响。
在Machine Learning In Action一书中,作者只实现了一个离散的二分类的分类器,我用C#实现了一个较通用的,可以处理离散或者连续的情况,也可以进行多个类别的分类,其中将概率分布抽象为一个类(Distribution),用户可以自己定义一个分布,也可以使用内置的二值分布或高斯分布,其中的DistributionFitter用于根据一组数据求出一个分布的参数,比如高斯分布的均值和方差,并返回这一分布。
以下是部分代码:
public class NaiveBayes<TLabel> where TLabel : IComparable
{
public class Category
{
public TLabel Label
{
get;
private set;
}
public double Frequency
{
get;
private set;
}
public Distribution[] FactorDistributions
{
get;
private set;
}
public Category(TLabel label, double frequency, Distribution[] distributions)
{
Label = label;
Frequency = frequency;
FactorDistributions = new Distribution[distributions.Length];
distributions.CopyTo(FactorDistributions, 0);
}
}
public Category[] Categories
{
get;
private set;
}
/// <summary>
/// High level training method. Use distributions defined by customers.
/// </summary>
/// <param name="categories">User defined categories</param>
public void Train(Category[] categories)
{
Categories = new Category[categories.Length];
categories.CopyTo(Categories, 0);
}
/// <summary>
/// Train a NaiveBayes with source samples.
/// </summary>
/// <param name="samples">Source samples. double[i] means the i-th eigen factor.</param>
/// <param name="labels">Labels of categories. Must have the same count with the samples</param>
/// <param name="distribution_fitter">A known distribution of each eigen factor</param>
public void Train(List<double[]> samples, TLabel[] labels, DistributionFitter distribution_fitter)
{
if (samples.Count != labels.Length)
throw new ArgumentException("'samples' has different count with 'labels'");
Dictionary<TLabel, List<double>[]> training_dict = new Dictionary<TLabel, List<double>[]>(new DicCmp<TLabel>());
int l = 0;
foreach (var sample in samples)
{
//Store all factors and their samples.
List<double>[] factor_table;
if (training_dict.ContainsKey(labels[l]))
{
factor_table = training_dict[labels[l]];
}
else
{
factor_table = new List<double>[sample.Length];
for (int i = 0; i < factor_table.Length; ++i)
{
factor_table[i] = new List<double>(samples.Count);
}
training_dict.Add(labels[l], factor_table);
}
//Add new sample to eigen factors.
for (int i = 0; i < factor_table.Length; ++i)
{
factor_table[i].Add(sample[i]);
}
++l;
}
Categories = new Category[training_dict.Count];
double total_sample_count = samples.Count;
int c = 0;
foreach (var category in training_dict)
{
Distribution[] distributions = new Distribution[category.Value.Length];
//Calculate each factor's distribution.
for (int i = 0; i < distributions.Length; ++i)
{
distributions[i] = distribution_fitter.Fit(category.Value[i].ToArray());
}
//Save every categories and their factors.
Categories[c] = new Category(category.Key, category.Value[0].Count / total_sample_count, distributions);
++c;
}
}
public TLabel Classify(double[] vector)
{
KeyValuePair<TLabel, double>[] label_prob_pairs = new KeyValuePair<TLabel, double>[Categories.Length];
int c = 0;
//Calculate each category's probability. Use log to avoid underflow.
foreach (var category in Categories)
{
double p = 0;
for (int i = 0; i < vector.Length; ++i)
{
p += Math.Log(category.FactorDistributions[i].GetProbability(vector[i]));
}
p += Math.Log(category.Frequency);
label_prob_pairs[c] = new KeyValuePair<TLabel, double>(category.Label, p);
++c;
}
//Sort via probability.
Array.Sort(label_prob_pairs, new SortCmp<TLabel>());
//The last item has the max probability.
return label_prob_pairs[label_prob_pairs.Length - 1].Key;
}
}最后总结一下朴素贝叶斯分类的优缺点。
优点:
1、存储容量小,训练完成后只需保存少许概率分布即可;
2、分类时计算量小,只需计算几个乘法或对数加法即可;
3、可以处理多分类问题;
4、实现也较简单;
缺点:
1、对准备的训练数据较敏感,数据量的大小与完备与否对训练结果有较大影响;
2、由于两个很强的假设,导致朴素贝叶斯分类在某些问题上效果不好,使用范围有限;
3、需要知道特征属性的概率分布,有时候概率分布是很难求得的。










 本文介绍了朴素贝叶斯分类的基本原理,包括贝叶斯定理的应用,以及朴素贝叶斯的两个核心假设。讨论了如何在训练过程中计算特征属性的概率分布,并提供了使用C#实现的通用分类器,支持离散和连续特征,同时指出该方法的优缺点及适用场景。
本文介绍了朴素贝叶斯分类的基本原理,包括贝叶斯定理的应用,以及朴素贝叶斯的两个核心假设。讨论了如何在训练过程中计算特征属性的概率分布,并提供了使用C#实现的通用分类器,支持离散和连续特征,同时指出该方法的优缺点及适用场景。
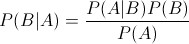
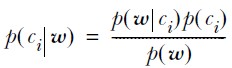

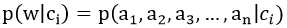
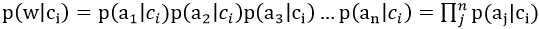
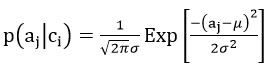
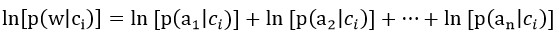
















 295
295

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








