在泛函分析中,卷积(捲積)、旋積、疊積或摺積,是通过两个函数f和g生成第三个函数的一种数学算子,表征函数f与经过翻转和平移的g的重叠部分的面积。如果将参加卷积的一个函数看作区间的指示函数,卷积还可以被看作是“移动平均”的推广。
卷积是分析数学中一种重要的运算。设: ,
, 是
是 上的两个可积函数,作积分:
上的两个可积函数,作积分:
可以证明,关于几乎所有的 ,上述积分是存在的。这样,随着
,上述积分是存在的。这样,随着 的不同取值,这个积分就定义了一个新函数
的不同取值,这个积分就定义了一个新函数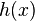 ,称为函数
,称为函数 与
与 的卷积,记为
的卷积,记为 。我们可以轻易验证:
。我们可以轻易验证: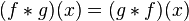 ,并且
,并且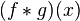 仍为可积函数。这就是说,把卷积代替乘法,
仍为可积函数。这就是说,把卷积代替乘法, 空间是一个代数,甚至是巴拿赫代数。
空间是一个代数,甚至是巴拿赫代数。
卷积与傅里叶变换有着密切的关系。例如两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换,利用此一性质,能简化傅里叶分析中的许多问题。
由卷积得到的函数 一般要比
一般要比 和
和 都光滑。特别当
都光滑。特别当 为具有紧支集的光滑函数,
为具有紧支集的光滑函数, 为局部可积时,它们的卷积
为局部可积时,它们的卷积 也是光滑函数。利用这一性质,对于任意的可积函数
也是光滑函数。利用这一性质,对于任意的可积函数 ,都可以简单地构造出一列逼近于
,都可以简单地构造出一列逼近于 的光滑函数列
的光滑函数列 ,这种方法称为函数的光滑化或正则化。
,这种方法称为函数的光滑化或正则化。
卷积的概念还可以推广到数列、测度以及广义函数上去。
具体定义:
函数f与g的卷积记作 ,它是其中一个函数翻转并平移后与另一个函数的乘积的积分,是一个对平移量的函数。
,它是其中一个函数翻转并平移后与另一个函数的乘积的积分,是一个对平移量的函数。
积分区间取决于f与g的定义域。
对于定义在离散域的函数,卷积定义为
参考:
维基百科













![(f * g)[m] = \sum_n {f[n] g[m - n]}](https://upload.wikimedia.org/math/8/7/d/87d76adca3c545f6832302da3f434c38.png)














 3748
3748

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








