线性代数
这一部分主要是对机器学习和深度学习用到的线性代数知识的总结,包括线性变换的物理意义与几何意义,直观的理解线性变换,以及特征值分解与奇异值分解的物理意义、几何意义,从信息的角度理解他们,最后,用线性代数实现PCA(从方差最大化角度)
线性变换
线性变换
变换是向量的的运动,变换让向量从一个地方(对应输入向量),运动到了另一个地方(对应输出向量)。

我们说将变换作用于某个空间,意思是将该变换应用于空间中的每一个向量。
空间中的向量可以用一些规则分布的点来表示。
下面是变换前的样子,

下面是变换后的样子。

变换后,空间中的点(即向量)运动到了其他的位置上。
二维空间变换中,等间距的平行网格可以更好地展示变换的性质。(下图是变换前后的等距线在同一坐标平面上的表示)

即线性变换是:
- 变换前后,所有的直线仍然是直线
- 变换前后,原点保持不变

换句话说,线性变换是原点不变,并使网络线保持平行且等距分布的变换。

线性变换的描述
以平面直接坐标系为例,假定我们有一个向量 v=[−1 2]。我们可以将它看成是 2 个基向量 i, j 的线性组合。线性组合的系数分别对应向量的 2 个分量。

在某个线性变换的作用下,i, j 以及 v 都运动到了新的位置。

线性变换前后网络线保持平行且等距分布,这一性质有一个重要的推论:线性变换后的 v 是变换后的 i 和 j 的线性组合,并且线性组合的系数和变换前一样(仍然是 -1 和 2)

即,线性变换前
i=[1 0],j =[0 1],则v =−1 [1 0]+2 [0 1]=[−1 2]
假定,经过某个线性变换后之后
i=[−1 2],j =[3 0],则v =−1 [1 −2]+2 [3 0]=[5 2]

所以,我们只要知道线性变换之后,i, j 的位置(坐标),就可以计算出任意一个向量经过同样的线性变换之后的位置(坐标)。

这意味着,对于一个线性变换,我们只需要跟踪基向量在变换前后的变化,就可以掌握整个空间(即全部向量)的变化。我们将线性变换后的基向量坐标按列组合起来,可以拼接成一个矩阵。线性变换的全部信息便都包含在这个矩阵当中了。

给定一个 2×2 的矩阵 [a c b d] 以及某个向量 [x y]。
矩阵对应着某个线性变换,它的 2 列 [a c] 和 [b d] 分别表示 2 个基向量 [1 0] 和 [0 1] 经过线性变换之后的坐标。

那么,向量 [x y] 经过该线性变换之后,其新坐标的计算方法如下:

将向量 [x y] 与矩阵 A相乘得到向量 b,即 Ax⃗ =b⃗ 。所以,矩阵相乘的意义是对向量做变换,即向量的运动。

常见的线性变换
对于线性变换,我们只需要跟踪原来的基向量在线性变换后的位置(坐标),然后把它们按列拼成一个矩阵,这个矩阵就是相应的线性变换矩阵。
旋转变换:
原来的 2 个基向量 [1 0] 和 [0 1] ,逆时针旋转90 度之后,变成了 [0 1] 和 [−1 0] ,把它们拼成 一个矩阵.这便是逆时针旋转 90 度对应的线性变换矩阵。

剪切变换:

投影变换:

常见的矩阵与变换
- 正交矩阵:将一组正交基旋转到另一组正交基,所以,对向量做旋转变换
- 实对称矩阵:对特征向量做且只做拉伸剪切变换
总之,线性变换是操纵空间的一种手段。线性变换保持原点不动,网格线平行且等距分布。只需要几个数字(变换后基向量的坐标)就可以清晰地描述一个线性变换。将变换后基向量的坐标按列拼接成一个矩阵。这个矩阵为我们提供了一种描述线性变换的语言。线性变换作用于一个向量,对应于用线性变换矩阵左乘该向量。
特征值分解
信息角度—-主成分分析
- 数据离散性越大,代表数据在所投影的维度上具有越高的区分度,这个区分度就是信息量
- 所以选取正确的坐标轴,然后根据各个维度上的数据方差大小,决定保留哪些维度的数据,这样的做法就是主成分分析的核心思想。
- 特征值对应的特征向量就是理想中想取得正确的坐标轴,而特征值就等于数据在旋转之后的坐标上对应维度上的方差。
- 在数据挖掘中,就会直接用特征值来描述对应特征向量方向上包含的信息量,而某一特征值除以所有特征值的和的值就为:该特征向量的方差贡献率(方差贡献率代表了该维度下蕴含的信息量的比例)。
奇异值分解SVD
- 正交矩阵 正交矩阵的行(列)向量都是两两正交的单位向量,正交矩阵对应的变换为正交变换,它有两种表现:旋转和反射。正交矩阵将标准正交基映射为标准正交基。
EVD
- 比如将x用A的所有特征向量表示为
- 通过第一个变换就可以把x表示为[a1 a2 … am]’:
- 在新的坐标系表示下,由中间那个对角矩阵对新的向量坐标换,其结果就是将向量往各个轴方向拉伸或压缩
- 最后一个变换就是U对拉伸或压缩后的向量做变换,由于U和U’是互为逆矩阵,所以U变换是U’变换的逆变换。
- 比如将x用A的所有特征向量表示为
3.SVD
- A=UDV’,U和V是两组正交单位向量,D是对角阵,表示奇异值,它表示我们找到了U 和V这样两组基,A矩阵的作用是将一个向量从V这组正交基向量的空间旋转到U这组正交基向量空间,并对每个方向进行了一定的缩放,缩放因子就是各个奇异值。如果V维度比U大,则表示还进行了投影。

- 特征值分解和奇异值分解都是给一个矩阵(线性变换)找一组特殊的基,特征值分解找到了特征向量这组基,在这组基下该线性变换只有缩放效果。而奇异值分解则是找到另一组基,这组基下线性变换的旋转、缩放、投影三种功能独立地展示出来了。
- 信息角度:奇异值往往对应着矩阵中隐含的重要信息,且重要性和奇异值大小相关。每个矩阵都可以表示为一系列秩为1的”小矩阵”之和,奇异值衡量这些小矩阵的对于矩阵的权重。
物理意义
- SVD提供了一种非常便捷的矩阵分解方式,能够发现数据中十分有意思的潜在模式。
- 主成分分析就是对数据的协方差矩阵进行了类似的分解(特征值分解),但这种分解只适用于对称的矩阵,而 SVD 则是对任意大小和形状的矩阵都成立。

- 我们可以看出矩阵的秩是3,也就是主要信息都包含在三个列向量里面
- 我们对矩阵进行奇异值分解以后,得到奇异值分别是σ1 = 14.72 σ2 = 5.22 σ3 = 3.31,矩阵A就可以表示成 A=u1σ1v1T+u2σ2v2T+u3σ3v3Tvi A = u 1 σ 1 v 1 T + u 2 σ 2 v 2 T + u 3








 本文深入浅出地介绍了机器学习中线性代数的基础知识,包括线性变换的物理和几何意义、特征值分解与奇异值分解的应用,以及如何从方差最大化角度理解PCA。通过实例解析线性变换矩阵、正交矩阵和奇异值分解,强调它们在数据降维和信息提取中的作用。
本文深入浅出地介绍了机器学习中线性代数的基础知识,包括线性变换的物理和几何意义、特征值分解与奇异值分解的应用,以及如何从方差最大化角度理解PCA。通过实例解析线性变换矩阵、正交矩阵和奇异值分解,强调它们在数据降维和信息提取中的作用。
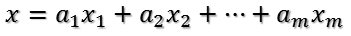
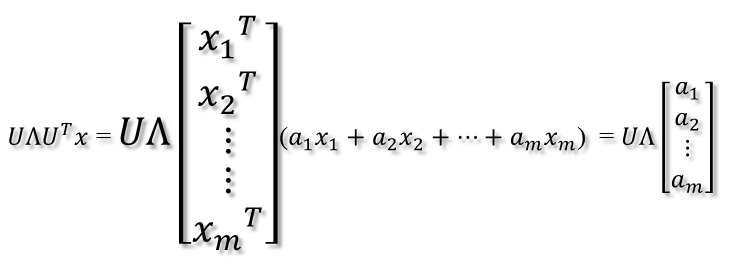
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1403
1403

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








