从零开始学《离散数学》-电子科技大学

1.1.1集合论基础 集合的初见

什么是集合？

定义

A set is a group of objects. (simplest way)

By a set we mean any collection M into a whole of definite distinct objects m (which

we called elements of M) of our perception or of our thought. (Cantor’s way)

集合 是由指定范围内的满足给定条件的所有对象聚集在一起构成，每一个对象称

为这个集合的元素。(In chinese)

外延公理 + 空集存在公理 + 无序对公理 + 并集公理 + 幂集公理 + 无穷公理 +

替换公理 + 正则公理 + 选择公理。(ZFC 公理化集合论)

例子

所有英文字母

所有小于 100 的正奇数

中国所有的残疾人

世界上所有的数学家

某植物园的所有植物

天安门广场所有的路灯和树

集合的符号表示

通常情况下

用带或不带下标的大写英文字母表示集合: A, B, C, · · · , A1, B1, C1, · · ·

用带或不带下标的小写英文字母表示元素: a, b, c, · · · , a1, b1, c1, · · ·

常用集合 (我们的老朋友)

自然数集合 N: 0, 1, 2, 3, · · ·

整数集合 Z: · · · , −2, −1, 0, 1, 2, · · ·

有理数集合 Q 与实数集合 R，等等

属于关系

若 a 是集合 A 中的元素，则称 a属于A，记为 a ∈ A

若 a 不是集合 A 中的元素，则称 a不属于A，记为 a ∈/ A

枚举法

列出集合中的全部元素或者仅列出一部分元素，其余用省略号 (· · · ) 表示。

A = {a, b, c, d}

B = {2, 4, 6, 8, 10, · · · }

叙述法

通过刻画集合中元素所具备的某种性质或特性来表示一个集合。

P = {x|P(x)}

A = {x|x是英文字母中的元音字母}

B = {x|x ∈ Z, x < 10}

C = {x|x = 2k, k ∈ N}

文氏图/Venn图

文氏图是利用平面上的点来做成对集合的图解方法。一般使用平面上的方形或圆

形表示一个集合，而使用平面上的一个小圆点来表示集合的元素。

基数

集合 A 中的元素个数称为集合的基数(base number)，记为 |A|

若一个集合的基数是有限的，称该集合为有限集(finite set)

若一个集合的基数是无限的，称该集合为无限集(infinite set)

A = {a, b, c}, |A| = 3

B ={ a, {b, c} }, |B| = 2

1.2.1集合论基础 特殊集合与集合间关系

空集

Definition

不含任何元素的集合叫做空集(empty set)，记作 ∅.

Example

设 A = {x|x ∈ R, x2 < 0}, 则 A = ∅

|∅| = 0, |{∅}| = 1

空集是绝对唯一的。

全集

Definition

针对一个具体范围，我们考虑的所有对象的集合叫做全集(universal set)，记作 U 或 E.

在文氏图一般使用方形表示全集。

Example

在立体几何中，全集是由空间的全体点组成的；

在我国的人口普查中，全集是由我国所有人组成的。

全集是相对唯一的。

集合的相等关系

元素的基本特性

集合中的元素是无序的。{1, 2, 3, 4} 与 {2, 3, 1, 4} 相同。

集合中的元素是不同的。{1, 2, 2, 3, 4, 3, 4, 2} 与 {1, 2, 3, 4} 相同。

citing example

设E = {x|(x − 1)(x − 2)(x − 3) = 0, x ∈ R}, F = {x|x ∈ Z+, x2 < 12},

可见 E 和 F 具有相同的元素 {1, 2, 3}, 此时称两个集合相等。

Theorem (外延性原理)

两个集合 A 和 B 相等，当且仅当它们的元素完全相同，记为 A = B, 否则 A 和 B 不相等，记为A ̸= B.

子集和真子集

citing example

设 A = {BASIC, PASCAL, ADA}, B = {ADA, PASCAL},

此时 A 中含有 B 中所有的元素，这种情况称为A 包含 B.

Definition

设 A, B 是任意两个集合，

如果 B 的每个元素都是 A 中的元素，则称 B 是 A 的子集，也称做B 被 A 包含或A 包含B，记作B ⊆ A，否则记作B ⊈ A.

如果 B ⊆ A 并且 A ̸= B，则称 B 是 A 的真子集，也称做B 被 A 真包含或A 真包含 B，记作B ⊂ A，否则记作B ̸⊂ A.

”⊆” 关系的数学语言描述为：B ⊆ A ⇔ 对 ∀x, 如果 x ∈ B, 则 x ∈ A.

文氏图:B ⊆ A

由子集定义可有

∅ ⊆ A

A ⊆ A

Example

已知 A = {1, 2, 3, 4}, B = {1, 2, 4}, C = {2, 3}, D = {3, 2}，可见

A ⊆ A, B ⊆ A, C ⊆ A, D ⊆ A,

C ⊆ D, D ⊆ C, 同时, C = D

证明集合相等

Theorem

设 A, B 为任意两个集合，则 A = B ⇔ A ⊆ B 并且 B ⊆ A

⋆⋆⋆ 上面的定理非常重要，这是证明集合相等的一种非常有效的方式。

证明框架

证明：

首先证明 A ⊆ B：∀x ∈ A, · · · , x ∈ B. ∴ A ⊆ B.

其次证明 B ⊆ A：∀x ∈ B, · · · , x ∈ A. ∴ B ⊆ A.

由以上两点，可知 A=B。

n 元集的子集

Example

设 A = {a, b, c}，求出 A 的所有子集。

解：由于 |A|=3，因而 A 的子集可能包含的元素个数 m = 0, 1, 2, 3

m = 0, 即没有任何元素，也就是空集 ∅

m = 1, 从 A 中任取 1 个元素，则有 C13 = 3 个：{a}, {b}, {c}

m = 2, 从 A 中任取 2 个元素，则有 C23 = 3 个：{a, b}, {b, c}, {a, c}

m = 3, 从 A 中任取 3 个元素，则有 C33 = 1 个：{a, b, c}

以上 8 个集合就是 A 的所有子集。

⋆ 推广: 对于任意 n 元集合 A，它的 m 元 (0 ⩽ m ⩽ n) 子集个数为  个,

所以不同的子集个数为：

幂集

Definition

设 A 为任意集合，把 A 的所有不同子集构成的集合叫做 A 的幂集(power set), 记作 P(A)，即，

x ∈ P(A) ⇔ x ⊆ A

P(A) = {x|x ⊆ A}

Example

设 A = {a, b, c}，B = a, {b, c} ，求他们的幂集 P(A) 和 P(B)。

解：P(A) = ∅, {a}, {b}, {c}, {a, b},{b, c}, {a, c}, {a, b, c}

P(B) = ∅, {a}, {b, c} ,{ a, {b, c}}

说明

幂集也叫做集族或集合的集合，对集族的研究在数学方面、知识库和表处理语言以及人工智能等方面都有十分重要的意义。

1.3.1集合论基础 集合的运算

并集

Definition

设 A, B 是两个集合，则集合 A 与 B 的并集定义为：

A ∪ B = {x|x ∈ A 或 x ∈ B}

Example

集合 {1, 3, 5} 和集合 {1, 2, 3} 的并集是 {1, 2, 3, 5};

若集合 A 是选修了音乐欣赏的学生，B 是选修了西方文学的学生，则 A ∪ B 是选修了音乐欣赏或选修了西方文学或两门课都同时选修的学生.

交集

Definition

设 A, B 是两个集合，则集合 A 与 B 的交集定义为：A ∩ B = {x|x ∈ A 并且 x ∈ B}

Example

集合 {1, 3, 5} 和集合 {1, 2, 3} 的交集是 {1, 3};

若集合 A 是选修了音乐欣赏的学生，B 是选修了西方文学的学生，则 A ∩ B 是即选修了音乐欣赏又选修了西方文学的学生.

补集

Definition

设 U 是全集，则集合 A 的补集定义为：

A = {x|x ∈/ A}

Example

集合 {1, 3, 5} 对于全集 {1, 2, 3, 4, 5, 6, 7, 8} 的补集是 {2, 4, 6, 7, 8};

若集合 A 是选修了音乐欣赏的学生，全集 U 是所有在校学生，则 A的 补集是没有选修音乐欣赏的学生.

差集

Definition

设 A, B 是两个集合，则集合 A 与 B 的差集定义为：A − B = {x|x ∈ A 并且 x ∈/ B}

Example

集合 {1, 3, 5} 和集合 {1, 2, 3} 的差集是 {5};

若集合 A 是选修了音乐欣赏的学生，B 是选修了西方文学的学生，则 A − B 是选修了音乐欣赏但没有选修西方文学的学生.

对称差集

Definition

设 A, B 是两个集合，则集合 A 与 B 的对称差集定义为：A ⊕ B = {x|(x ∈ A 并且 x ∈/ B)或者(x ∈/A 并且 x ∈ B)}

Example

集合 {1, 3, 5} 和集合 {1, 2, 3} 的对称差集是 {2, 5};

若集合 A 是选修了音乐欣赏的学生，B 是选修了西方文学的学生，则 A ⊕ B 是只选修了音乐欣赏和西方文学两门课中某一门的学生.

并集和交集的扩展

Definition

设 A1, A2, · · · , An 是任意 n 个集合，则这 n 个集合的并集是包含那些至少是这组集合中一个集合成员的元素的集合，即

 

Definition

设 A1, A2, · · · , An 是任意 n 个集合，则这 n 个集合的交集是包含那些属于这组集合中所有集合成员的元素的集合，即

Example

设 A = {0, 2, 4, 6, 8}, B = {0, 1, 2, 3, 4}, C = {0, 3, 6, 9}，则

A ∪ B ∪ C = {0, 1, 2, 3, 4, 6, 8, 9}

A ∩ B ∩ C = {0}

1.4.1集合论基础 集合的运算定律

集合运算的基本等式

Theorem

设 U 为全集，A, B, C 为任意集合。

1 A ∪ A = A, A ∩ A = A.(幂等律)

2 A ∪ B = B ∪ A, A ∩ B = B ∩ A.(交换律)

3 A ∪ (B ∪ C) = (A ∪ B) ∪ C, A ∩ (B ∩ C) = (A ∩ B) ∩ C.(结合律)

4 A ∪ ∅ = A, A ∩ U = A.(同一律)

5 A ∪ U = U, A ∩ ∅ = ∅.(零律)

6 A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C), A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C).(分配律)

7 A ∪ (A ∩ B) = A, A ∩ (A ∪ B) = A.(吸收律)

8 ∩ A = ∅,  ∪ A = U.(矛盾律和排中律)

9 = A.(双重否定律)

10  =  ∩ ,   =  ,(德摩根律)

集合相等的证明

回顾证明方法

如需证明集合 A 和 B 相等，通常的方法是证明两个集合间的相互包含关系，即

A = B⇔ A ⊆ B 并且 B ⊆ A

而证明集合的包含关系则使用如下方法：B ⊆ A ⇔ ∀x ∈ B, x ∈ A

证明：

首先证明 A ⊆ B：∀x ∈ A, · · · , x ∈ B. ∴ A ⊆ B.

其次证明 B ⊆ A：∀x ∈ B, · · · , x ∈ A. ∴ B ⊆ A.

由以上两点，可知 A=B。

可用于证明德摩根律的等式之一： =  ∩ ,

1.5.1集合论基础 可数集合与不可数集合

有限 → 无限，量变 → 质变

皮亚诺公理自然数集的定义

1891 年, 意大利数学家皮亚诺公开发表了基于序数的自然数定义公理。这组公理包括：

• 0 是自然数

• 每个自然数 n 都有一个后继，这个后继也是一个自然数，记为 S(n)；
• 两个自然数相等当且仅当它们有相同的后继，即 m = n 当且仅当 S(m) = S(n)；
• 没有任何自然数的后继是 0；
• (归纳公理) 若 φ 是关于一个自然数的预测，如果❶φ(0) 为真；❷当 φ(n) 为真，则有 φ(S(n)) 为真；则 φ(n) 对任意自然数 n 都成立(数学归纳法)

冯 • 诺依曼的自然数定义

20 世纪初，集合称为数学的基本概念之后，数学奇才，计算机之父冯 • 诺依曼基于基数，利用一个集合的序列来定义自然数：

• ∅ ∈ N
• 若n ∈ N, 则n′ ≡ n ∪ {n} ∈ N。

从而，这个集合序列的基数就可以来定义自然数：

0 ≡ |∅|;

1 ≡ |∅ ∪ {∅}| = |{∅}|;

2 ≡ |{∅} ∪ {{∅}}| = |{∅, {∅}}|;

.......

如何比较集合的大小？

比较下列的集合对，哪一个的元素个数更多？

集合 {1, 2, 3} 与集合 {a, b, c, d, · · · , x, y, z}

自然数集合 N = {0, 1, 2, · · · } 与奇数集合 {1, 3, 5, 7, · · · }

对于两个有限集合而言，比较二者的大小只需要看集合的基数，但对于无限集合

却没有这么简单。如何比较无限集合的“大小”呢？这里需要采用一种通过判断

两个无限集合之间是否存在一种一一对应的关系来解决这个问题。

等势

定义

设 A, B 为两个集合，若在 A, B 之间存在一种一一对应的关系：Ψ : A → B

则称 A 与 B 是等势的 (equipotential)，记作：A ∼ B

由等势定义可以看出，如果 A = B，那么 A ∼ B，反之却不成立

可数集合

定义

凡与自然数集合 N 等势的集合，称为可数集合(countable set)，该集合的基数记为ℵ0(读作阿列夫零)

例子

试证明下列集合都是可数集合.

(1)  = {x|x ∈ N, x是正奇数};

(2) P = {x|x ∈ N, x是素数};

(3) 有理数集合Q;

证明

在  与 N 之间建立一个一一对应关系 φ1 : N → O+ 如下:

所以   是可数集合

在 P 与 N 之间建立一个一一对应关系 φ2 : N → P 如下:

所以 P 是可数集合

有理数集合 Q

在 Q 与 N 之间建立一个一一对应关系 φ3 : N → Q 如下图所示。

注意，所有有理数以p/q 的形式表示，其上标表示对应的自然数。

所以 Q 是可数集合。

从有限到无限，不仅仅是简单数量上的变化 (量变)，而引起了本质的改变 (质变)。

两个无限集合的“大小”已经不能单纯使用集合中的元素个数来衡量。

ℵ0表示一切可数集合的基数，是一种抽象的表达。

表面上个数完全不相等的两个集合之间仍可能存在等势关系，如集合与其真子集之间，这体现了有限集合和无限集合的根本差别。

不可数集合

定义

开区间 (0, 1)称为不可数集合，凡与开区间 (0, 1) 等势的集合，称为不可数集合，该类集合的基数记为ℵ(读作阿列夫)

例子

2.1.1命题逻辑 什么是命题

数理逻辑的起源和发展

什么是命题

注意：数理逻辑研究的中心问题是推理，而推理的前提和结论都是命题。因而命题是推理的基本单位。

Definition

具有确切真值的陈述句称为命题(proposition)。该命题可以取一个“值”，称为真值。真值只有“真”和“假”两种，分别用“T”(或“1”) 和“F”(或“0”)表示。

Example

成都是一个旅游城市。真值：T

北京是中国的首都。真值：T

3 能被 2 整除。真值：F

非命题

注意：一切没有判断内容的句子，如命令句 (或祈使句)、感叹句、疑问句、二义性的陈述句等都不能作为命题。

Example

这个语句是假的；

x + y > 0；

把门关上；

滚出去！

你要出去吗？

复合命题 (如何产生新命题)

Example

四川不是一个国家；

3 既是素数又是奇数；

张谦是大学生或是运动员；

如果周末天气晴朗，则我们将到郊外旅游；

两个三角形全等当且仅当三角形的三条边全部相等。

Definition

原子命题 (简单命题)：不能再分解为更为简单命题的命题。

复合命题：可以分解为更为简单命题的命题。这些简单命题之间是通过如“或者”、“并且”、“不”、“如果......则...... ”、“当且仅当”等这样的关联词和标点符号复合而成。

约定：通常用大写的带或不带下标的英文字母表示命题 (包括原子命题和复合命题)。A,B,C,· · · ,P,Q,R,· · · , Ai,Bi,Ci,· · · ,Pi,Qi,Ri,· · ·

2.2.1命题逻辑 命题联结词

引入

注意：回顾复合命题中，一般是通过联结词和标点符号将简单命题联结成复杂的语句，最常见的联结词主要有以下五种：“或者”、“并且”、“不”、“如果......       则......”、“当且仅当”

Example

四川不是一个国家；

3既是素数又是奇数；

张谦是大学生或是运动员；

如果周末天气晴朗，则我们将到郊外旅游；

两个三角形全等当且仅当三角形的三条边全部相等

否定联结词

Definition

设 P 是任意一个命题，复合命题“非 P”(或 “P 的否定”)称为 P 的否定式(negation)，记作¬P，

“¬” 为否定联结词。P 为真当且仅当 ¬P 为假。

“¬” 是自然语言中的 “非”、“不”、“没有” 等的逻辑抽象

合取联结词

Definition

设 P、Q 是任意两个命题，复合命题“P 并且 Q”(或 “P 和 Q”)称为 P 与 Q 的合取式(conjunction)，

记作P ∧ Q，“∧” 为合取联结词。P ∧ Q 为真当且仅当 P，Q 同为真

注意

“∧” 是自然语言中的 “并且”、“既…又…”、“但”、“和”、“与”、“不仅…而且…”、“虽然…但

是…”、“一面…, 一面…” 等的逻辑抽象；但不是所有的“和”，“与”都要使用合取联结词

表示，要根据句子的语义进行分析。

例如

2 和 3 的最小公倍数是 6；

点 a 位于点 b 与点 c 之间。

这两个命题都是简单命题，不能再分。

析取联结词

Definition

设 P、Q 是任意两个命题，复合命题“P 或 Q”称为 P 与 Q 的析取式(disjunction)，记作P ∨ Q，

“∨” 为析取联结词。P ∨ Q 为真当且仅当 P，Q 至少有一个为真

注意

联结词 “∨” 是自然语言中的 “或”、“或者” 等的逻辑抽象。自然语言中的 “或” 有 “可兼

或”(或称为同或)、“不可兼或”(即异或) 两种。严格来讲，析取联结词实际上代表的是可兼

或，异或有时会使用单独的异或联结词 “⊕” 或 “” 来表示。

例子

命题：张红生于 1982 年或 1983 年，令

P: 张红生于 1982 年；

Q: 张红生于 1983 年。

P 与 Q 不能同时为真，即为“不可兼或”。

蕴涵联结词

Definition

设 P、Q 是任两个命题，复合命题“如果 P，则 Q”称为 P 与 Q 的蕴涵式(implication)，记

作P → Q，“→” 为蕴涵联结词。P → Q 为假当且仅当 P 为真且 Q 为假。一般把蕴涵式 P → Q

中的 P 称为该蕴涵式的前件，Q 称为蕴涵式的后件。

注意

在自然语言中，前件为假，不管结论真假，整个语句的意义，往往无法判断。但对于数理

逻辑中的蕴涵联结词来说，当前件 P 为假时，不管 Q 的真假如何，则 P → Q 都为真。此

时称为 “善意推定”。

例子

命题：如果角 A 和角 B 是对顶角，则角 A 等于角 B。

这个命题是我们非常熟悉的一个定理，当然是真命题。当前件为假时，这个定理依然成立。

例子

设 P：约翰学习微积分，Q：约翰是大学一年级学生。则以下的复合命题均可用 P → Q 表示

如果约翰学习微积分，则他是大学一年级学生。如果 P，则 Q

因为约翰学习微积分，所以他是大学一年级学生。因为 P，所以 Q

只要约翰学习微积分，他就是大学一年级学生。只要 P，就 Q

约翰学习微积分仅当他是大学一年级学生。P 仅当 Q

只有约翰是大学一年级学生，他才能学习微积分。只有 Q，才 P

除非约翰是大学一年级学生，他才能学习微积分。除非 Q，才 P

除非约翰是大学一年级学生，否则他不学习微积分。除非 Q，否则 ¬P

等价联结词

Definition

设 P、Q 是任两个命题，复合命题“P 当且仅当 Q”称为 P 与 Q 的等价式(equivalence)，记

作P ↔ Q，“↔” 为等价联结词(也称作双条件联结词)。P ↔ Q 为真当且仅当 P、Q 同为真假。

“↔” 是自然语言中的 “等价”、“充分必要条件”、“当且仅当” 等的逻辑抽象。

2.3.1命题逻辑 命题符号化及其应用

回顾命题联结词

命题联接词 “∧”、“∨”、“↔” 具有对称性，而 “¬”、“→” 没有

命题联结词的真值表

联结词是两个命题真值之间的联结，而不是命题内容之间的连接，

因此复合命题的真值只取决于构成他们的各简单命题的真值，而与它们的内容无关，与二者之间是否有关系无关

Example

命题 1：雪是白的当且仅当北京是中国的首都。

命题 2：如果 2 是偶数，则天上就可以掉馅饼。

尽管两个简单命题的内容之间无关联，但二者均为合法命题，且具有确定的真值。

命题联结词的优先级

优先级顺序

• 所有五个联接词的优先顺序为：否定，合取，析取，蕴涵，等价；
• 同级的联结词，按其出现的先后次序 (从左到右)；
• 若运算要求与优先次序不一致时，可使用括号；同级符号相邻时，也可使用括号。括号中的运算为最高优先级。

Example

¬P ∨ ¬Q → R ∧ S ↔ T 的运算步骤是如何呢？

¬P ∨ (¬Q → R) ∧ S ↔ T的运算步骤又是如何？

复合命题符号化

设命题       P : 你陪伴我;      Q : 你代我叫车子;      R : 我将出去

符号化下述语句：

如果你陪伴我并且代我叫辆车子，则我将出去。符号化为：(P ∧ Q) → R

如果你不陪伴我或不代我叫辆车子，我将不出去。符号化为：(¬P ∨ ¬Q) → ¬R

除非你陪伴我或代我叫车子，否则我将不出去。符号化为：R → (P ∨ Q) 或 (¬P ∧ ¬Q) → ¬R

命题联接词与开关电路

设命题 P；开关 S1 闭合；命题 Q；开关 S2 闭合。则用复合命题表示：

(图 1) 开关电路的 “串联”：P ∧ Q

(图 2) 开关电路的 “并联”：P ∨ Q

(图 3) 开关电路的 “断开”：¬P

命题联接词与逻辑电路

命题联接词 “∧”、“∨”、“¬” 对应于与门、或门和非门电路，从而命题逻辑是计算机硬件

电路的表示、分析和设计的重要工具。

命题联接词与网页检索

布尔检索

在布尔检索中，联接词 “∧”（一般用 AND 表示）用于匹配包含两个检索项的记

录，联接词 “∨”（一般用 OR 表示）用于匹配包含两个检索项至少一个的记录，

而联接词 “¬”（一般用 NOT 表示）用于排除某个特定的检索项

例子

New AND Mexico AND universities：

检索新墨西哥州各大学的网页。

(New AND Mexico OR Arizona) AND universities：

检索新墨西哥州或亚利桑那州各大学的网页。

命题联接词与位运算

位运算

计算机中的信息采用二进制的方式来表达。每个二进制位只能是 1 或 0，可对应于某一个布尔变量的真值。

当我们需要判断该布尔变量的真值时，就可以利用按位与（bitwiseAND）或按位或（bitwise OR）以及按位取反（bitwise NOT）等来操作

这是 TCP/IP 网络协议栈中的 IP 报头的基本格式，考虑：如何获取版本号？ipdata[0]&0xF0 >> 4

2.4.1命题逻辑 命题公式和真值表

命题变元

定义：一个特定的命题是一个常值命题，它不是具有值 “T”(“1”)，就是具有值 “F”(“0”)

一个任意的没有赋予具体内容的原子命题是一个变量命题，常称它为命题变量 (或命题变元)(propositional variable)，

该命题变量无具体的真值，它的变域是集合{T, F}(或 {0, 1})

 

复合命题是由原子命题与联结词构成的命题。

所以，当其中的原子命题是命题变元时，此复合命题也即为命题变元的函数，且该函数的值仍为“真”或“假”值，

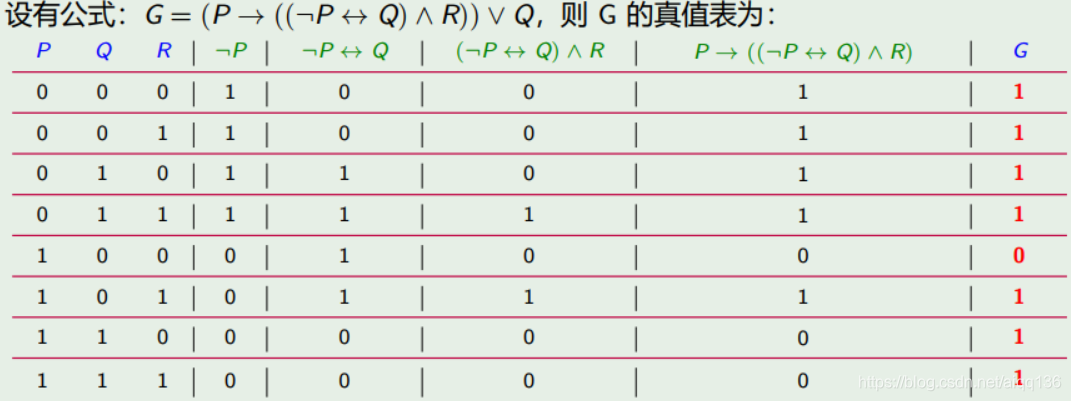
这样的函数可形象地称为“真值函数” 或 “命题公式”，此命题公式没有确切的真值。例如：G = P ∧ Q → ¬R.

命题公式

定义

命题演算的合式公式 (well formed formula，wff)，又称命题公式 (简称公式)，按如下规则生成：

1. 命题变元本身是一个公式；（如：P, Q, R, · · · ）
2. 如 G 是公式，则(¬G)也是公式；（如：¬P, ¬Q, ¬R, · · · ）
3. 如 G，H 是公式，则(G ∧ H)、(G ∨ H)、(G → H)、(G ↔ H)也是公式；（如：P ∧ Q, (¬Q) → R, · · · ）

仅由有限步使用规则 (1)、(2)、(3)后所得到的包含命题变元、联结词和括号的符号串才是命题公式.（如：¬(P ∧ Q) ↔ R, (¬Q ∨ (P ∧ ¬R)) → R, · · · ）

如果 G 是含有 n 个命题变元 P1、P2、P3、· · · 、Pn 的公式，可记为：G(P1, P2, P3, · · · , Pn) 或简写为 G。

说明

• 原子命题变元是最简单的合式公式，称为原子合式公式，简称原子公式；
• 命题公式没有真值，只有对其命题变元进行真值指派后，方可确定命题公式的真值；
• 整个公式的最外层括号可以省略；公式中不影响运算次序的括号也可以省略。
• 在实际应用中，为了便于存储和运算，命题公式常用二元树的方式来表达。

公式的解释

定义

设 P1、P2、P3、· · · 、Pn 是出现在公式 G 中的所有命题变元，

指定 P1、P2、P3、· · · 、Pn 一组真值，则这组真值称为 G 的一个解释，常记为 I。

例子

设有公式：G = P → (¬Q ∧ R)

P = 0, Q = 1, R = 0是 G 的一个解释，使得 G 的真值为 1。

P = 1, Q = 0, R = 0是 G 的一个解释，使得 G 的真值为 0。

如果公式 G 在解释 I 下是真的，则称I 满足 G，此时 I 是 G 的成真赋值；

如果 G 在解释 I 下是假的，则称I 弄假于 G，此时 I 是 G 的成假赋值。

真值表

一般来说，若有 n 个命题变元，则应有 个不同的解释。

利用真值表，可得到公式的所有成真赋值和成假赋值。

定义

由公式 G 在其所有可能的解释下所取真值构成的表，称为 G 的真值表(truth table)

真值表画法

一般我们将公式中的命题变元放在真值表的左边，将公式的结果放在真值表的右边。有时为了清楚起见，可将求公式的中间结果也放在真值表中。

2.5.1命题逻辑 命题公式的分类和等价

真值表告诉我们什么？

命题公式分类

Definition

公式 G 称为永真公式(重言式,tautology)，如果在它的所有解释之下其真值都为“真”。

公式 G 称为永假公式(矛盾式,contradiction)，如果在它的所有解释之下其真值都为“假”。有时也称永假公式为不可满足公式。

公式 G 称为可满足公式(satisfiable)，如果它不是永假的

三种特殊公式之间的关系

1. G 是永真的当且仅当 ¬G 是永假的；
2. G 是可满足的当且仅当至少有一个解释 I，使 G 在 I 下为真。
3. 若 G 是永真式，则 G 一定是可满足式，但反之可满足公式不一定是永真式；

命题公式分类

公式的等价

考虑上一个例子中的永真公式 G1 = (P → Q) ↔ (¬P ∨ Q)，将这个公式拆开，令G = P → Q，H = ¬P ∨ Q，

从而 G1 = G ↔ H，由于 G1 是永真公式，根据等价联接词的定义可知 G,H 必同为真或者同为假。此时我们称公式 G,H 具有逻辑等价关系。

Definition

设 G，H 是两个命题公式，P1，P2，P3，· · · ，Pn是出现在 G，H 中所有的命题变元，如果对于

P1，P2，P3，· · · ，Pn 的 个解释，G 与 H 的真值结果都相同，则称公式 G 与 H 是等价的，

记作G = H。（或G ⇔ H）

公式等价的充分必要条件

Theorem

对于任意两个公式 G 和 H，G = H 的充分必要条件是公式 G ↔ H 是永真公式。

Proof.

必要性：假定 G = H，则 G，H 在其任意解释 I 下或同为真或同为假，于是由 “↔” 的意义知，公式 G ↔ H 在其任何的解释 I 下，其真值为“真”，即 G ↔ H 为永真公式。

充分性：假定公式 G ↔ H 是永真公式，I 是它的任意解释，在 I 下，G ↔ H 为真，因此，G，H 或同为真，或同为假，由于 I 的任意性，故有 G = H。

命题公式的可判定性

可判定性: 能否给出一个可行方法，完成对任意公式的判定类问题。（类型或等价判定）

命题公式是可判定的。

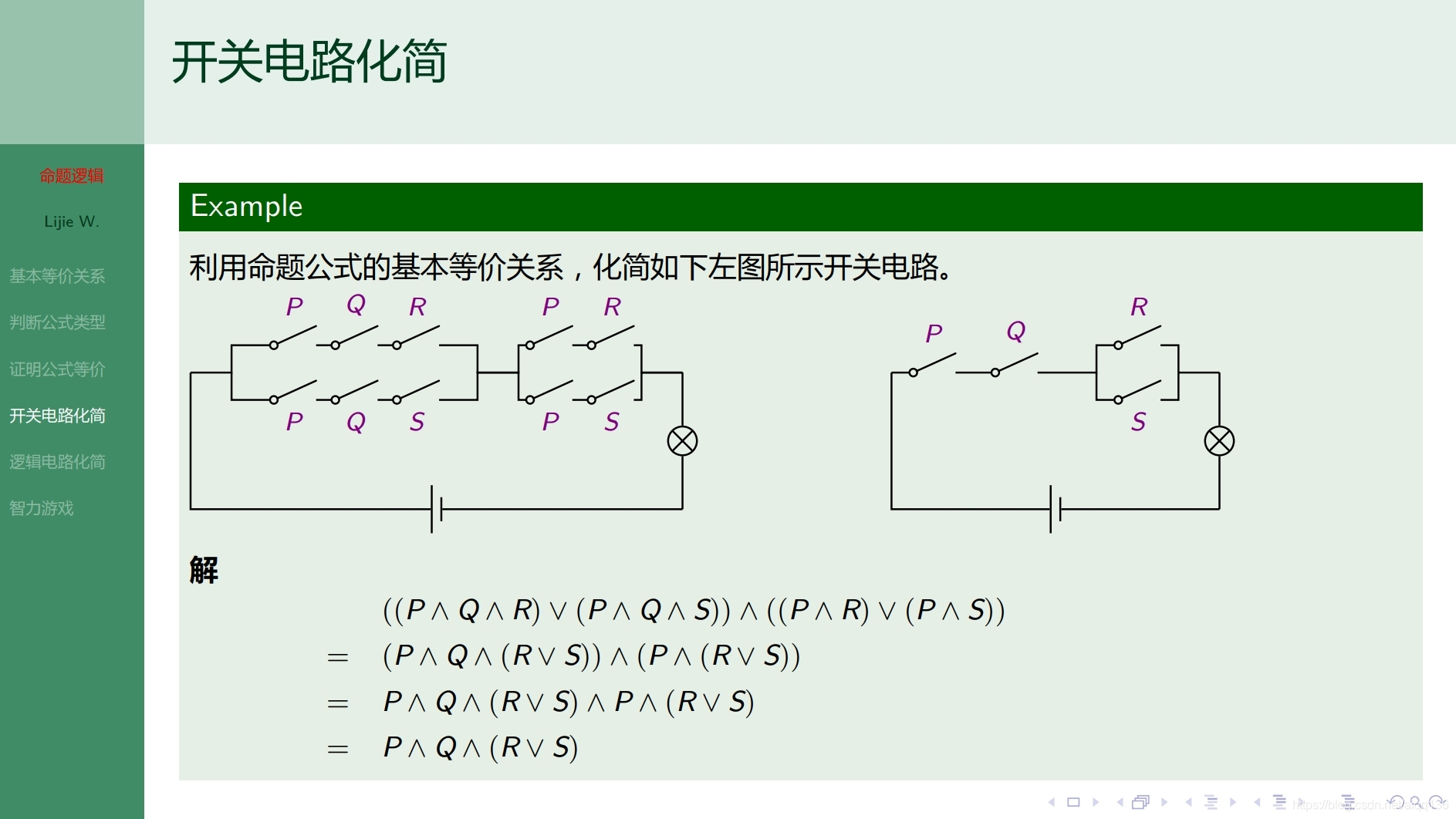
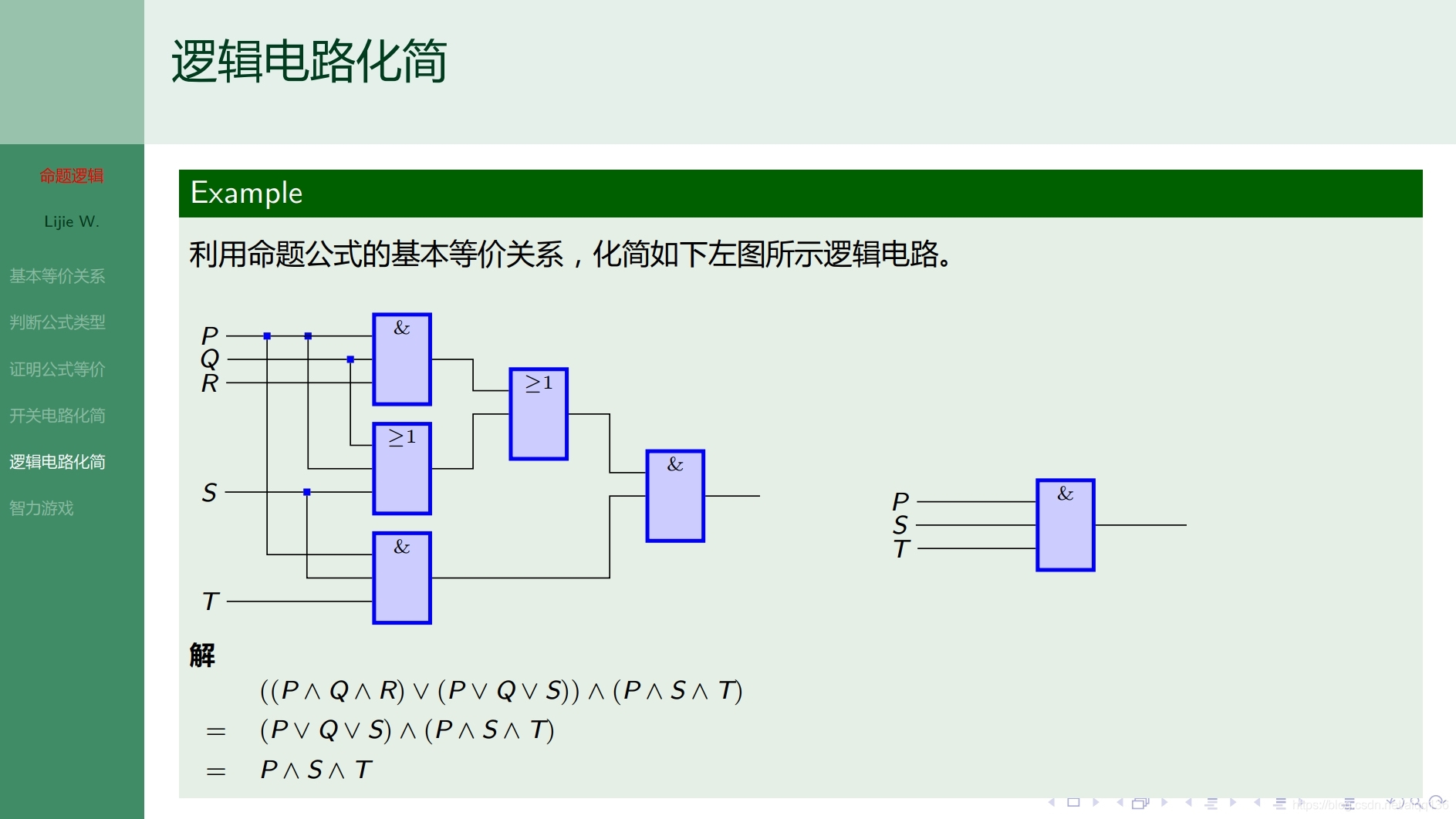
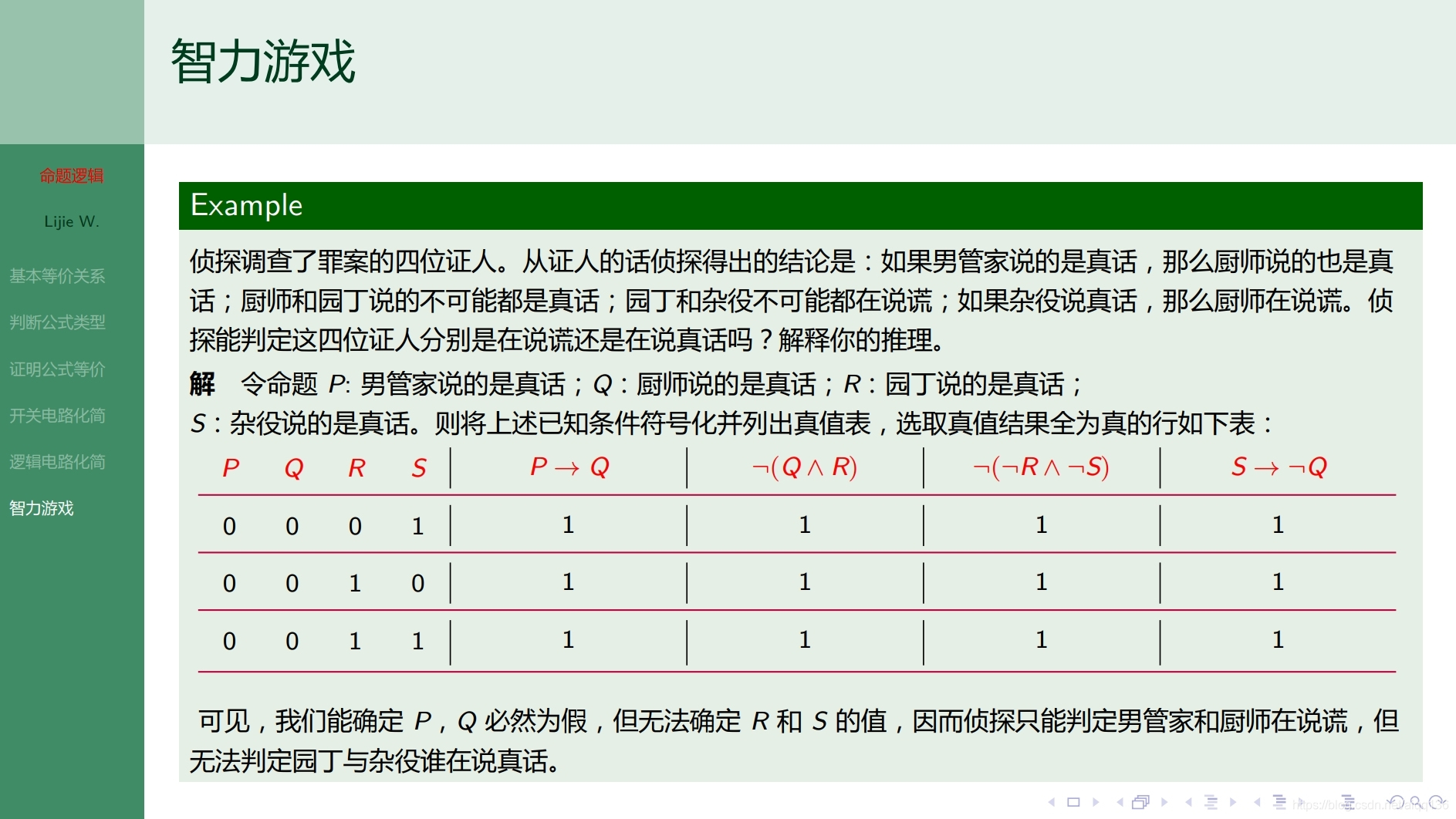
2.6.1命题逻辑 基本等价关系及其应用

3.1.1命题逻辑 范式

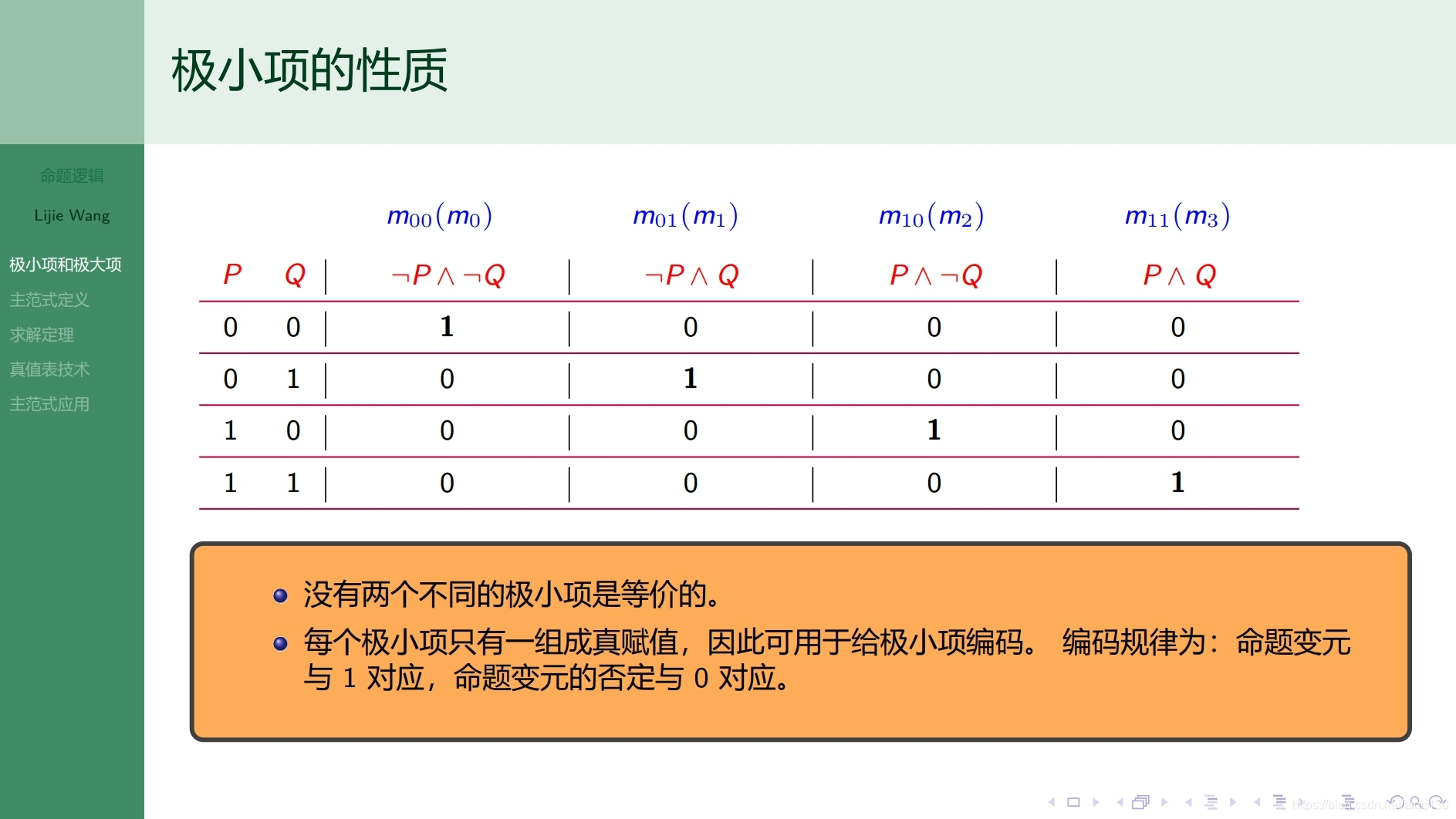
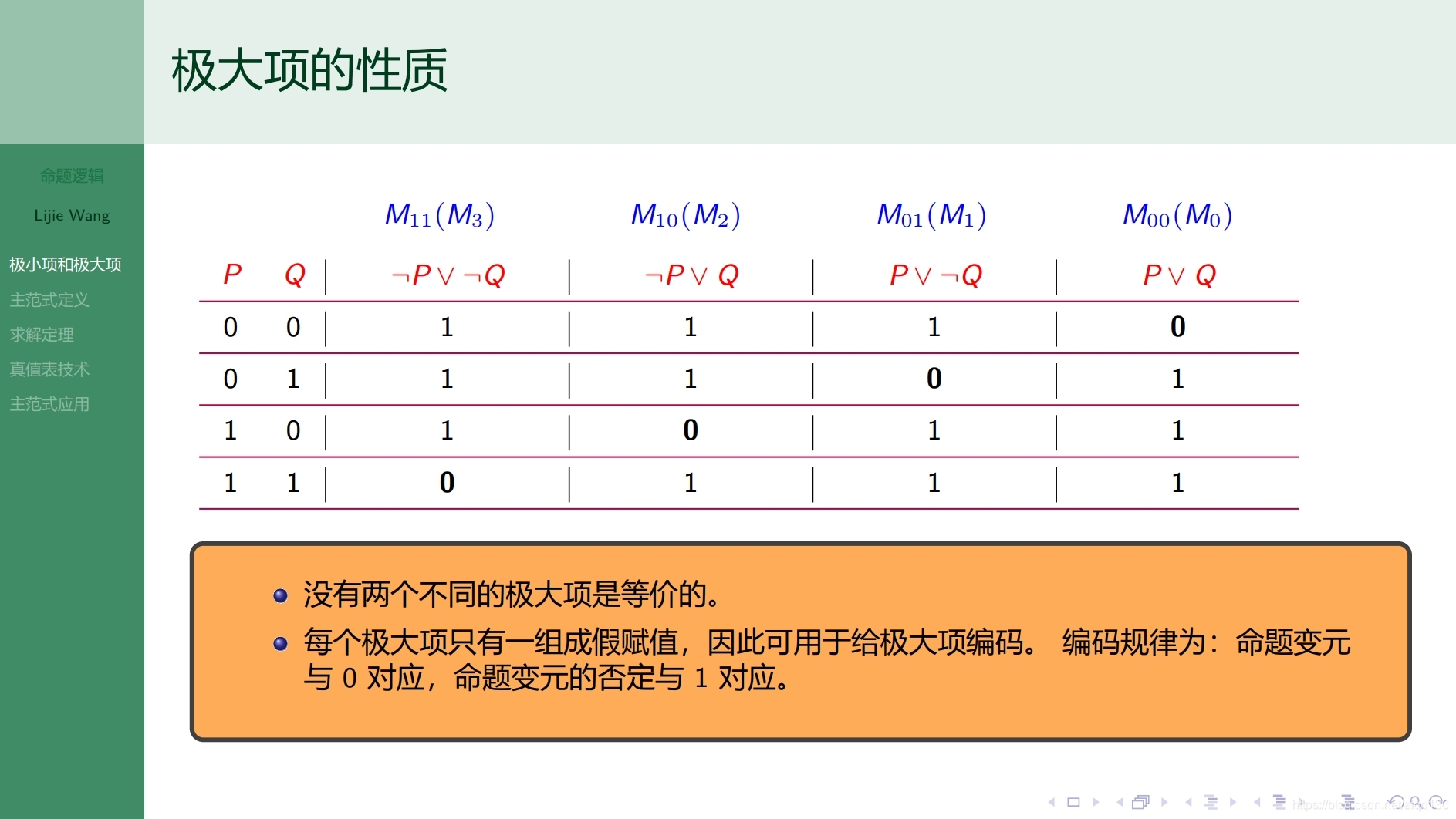
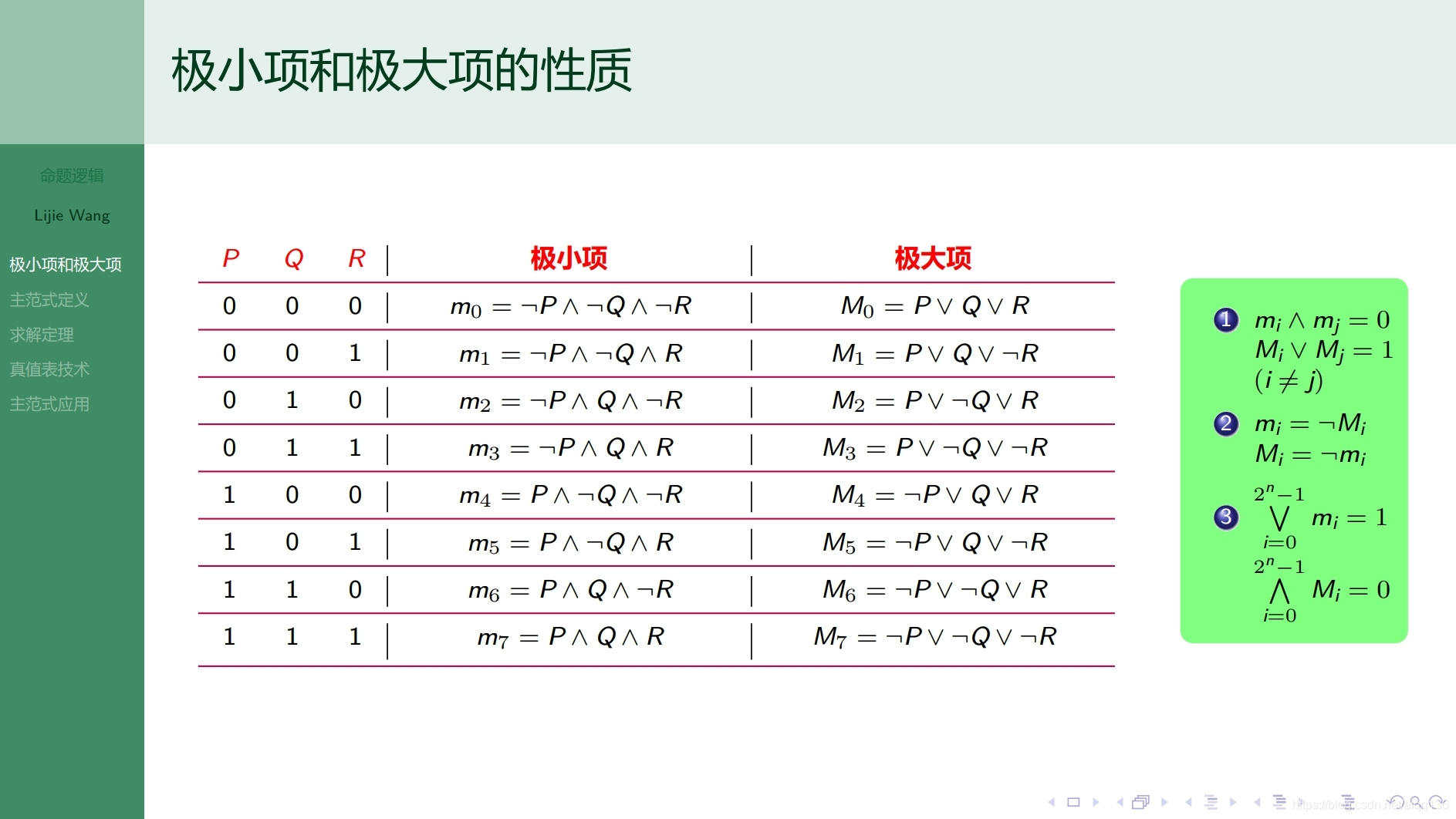
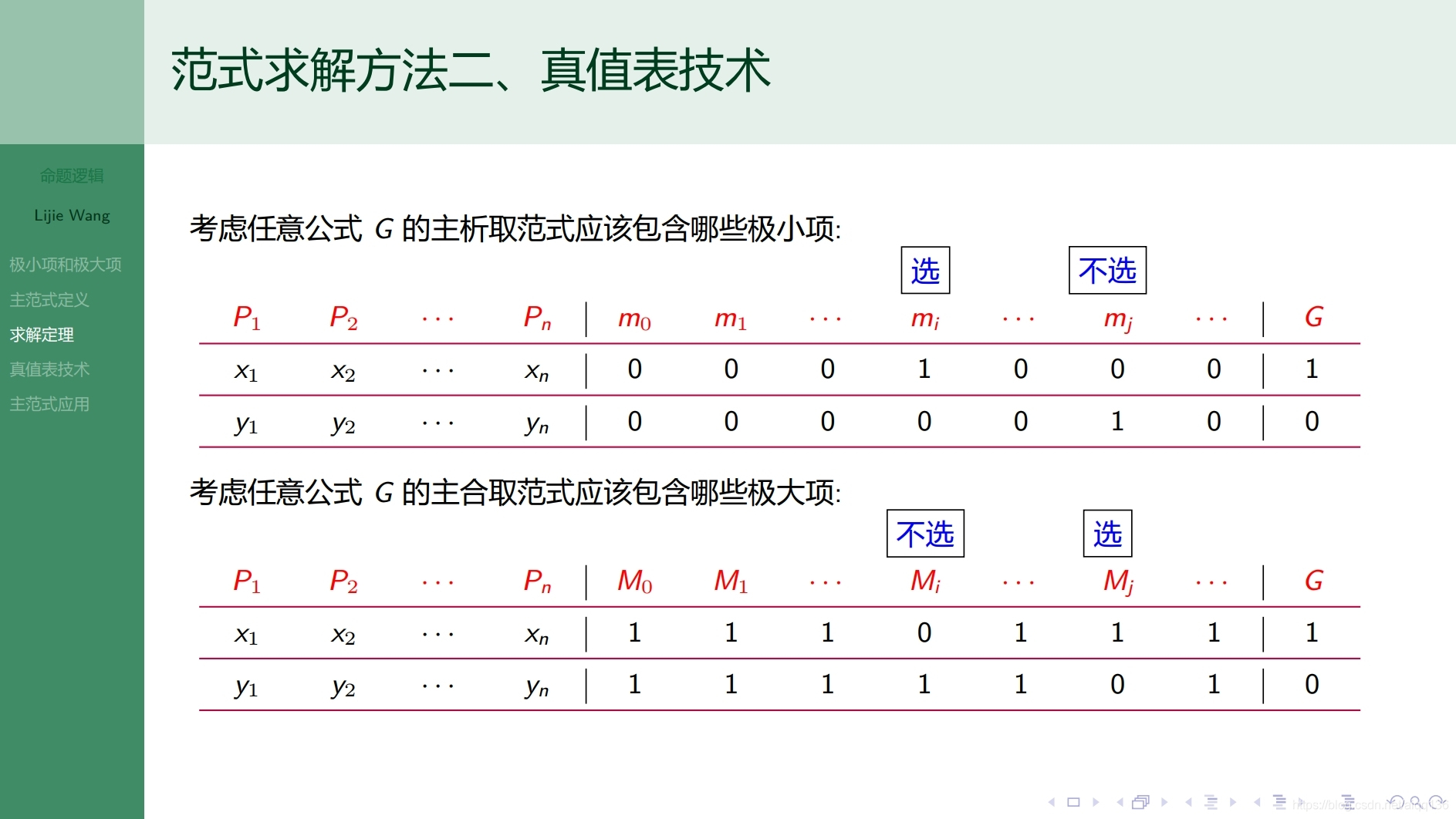
3.2.1命题逻辑 主范式

3.3.1命题逻辑 基本推理形式和蕴含关系

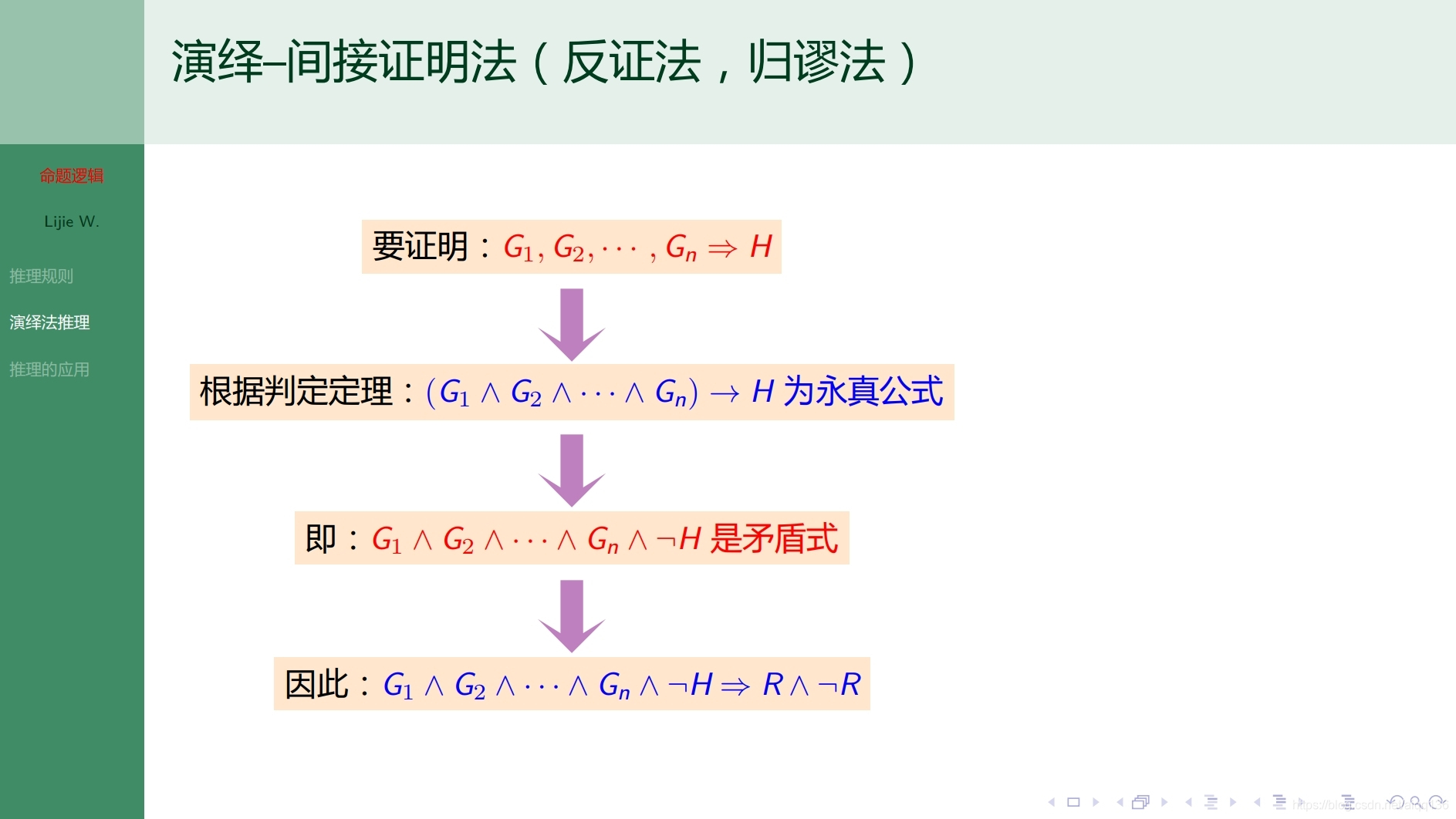
3.4.1命题逻辑 自然演绎法推理

4.1.1谓词逻辑 谓词的引入

4.2.1谓词逻辑 量词的引入

4.3.1谓词逻辑 谓词符号化举例

4.4.1谓词逻辑 谓词合式公式

4.5.1谓词逻辑 自由变元与约束变元

5.1.1谓词逻辑 公式的解释与分类

5.2.1谓词逻辑 公式的等价关系

5.3.1谓词逻辑 前束范式

5.4.1谓词逻辑 推理形式和推理规则

5.5.1谓词逻辑 综合推理方法

6.1.1二元关系 序偶和笛卡儿积

6.2.1二元关系 关系的定义

6.3.1二元关系 关系的表示

6.4.1二元关系 关系的运算

6.5.1二元关系 关系的运算定律

6.6.1二元关系 关系的幂运算

6.7.1二元关系 关系的性质（一）

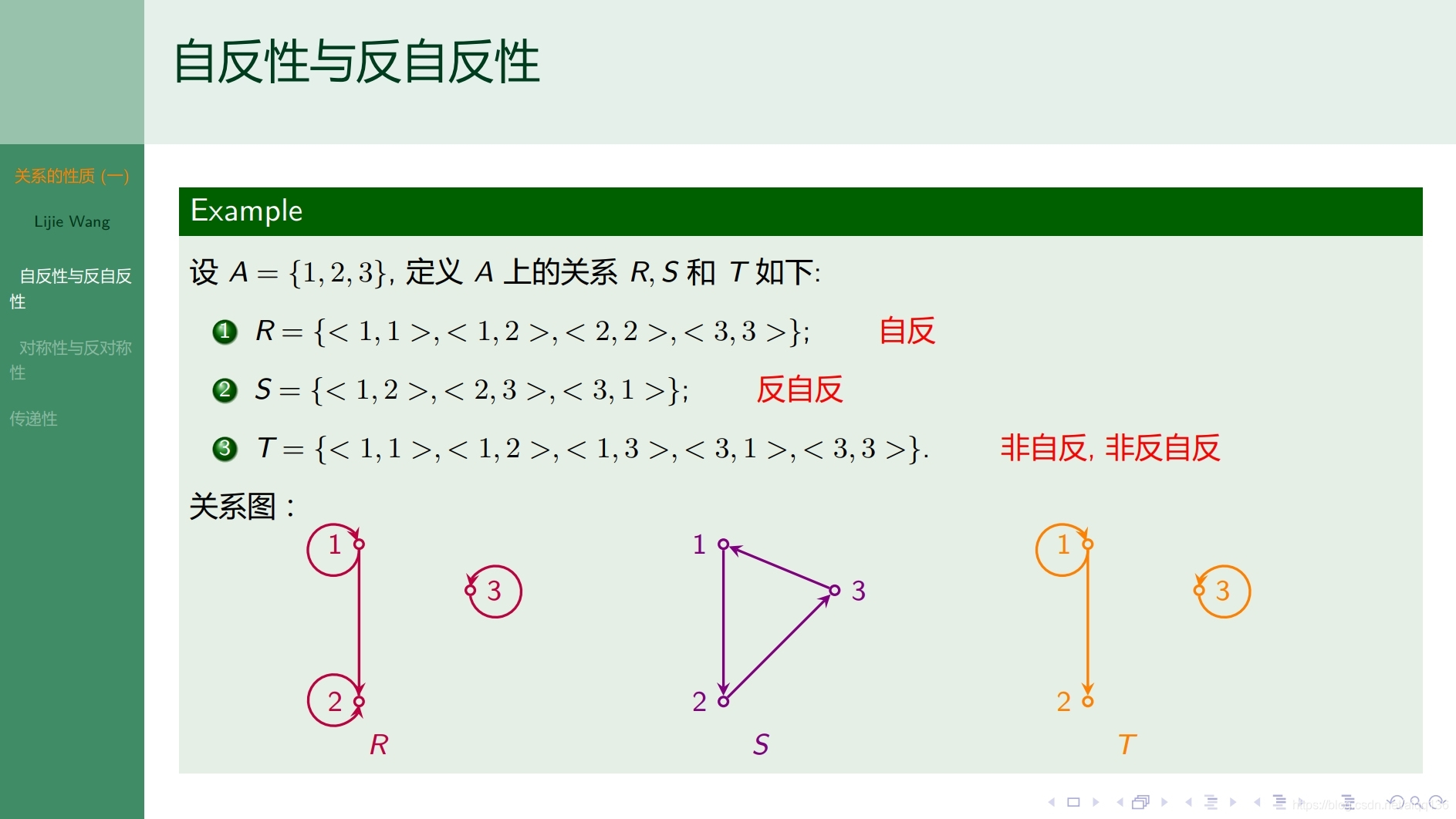
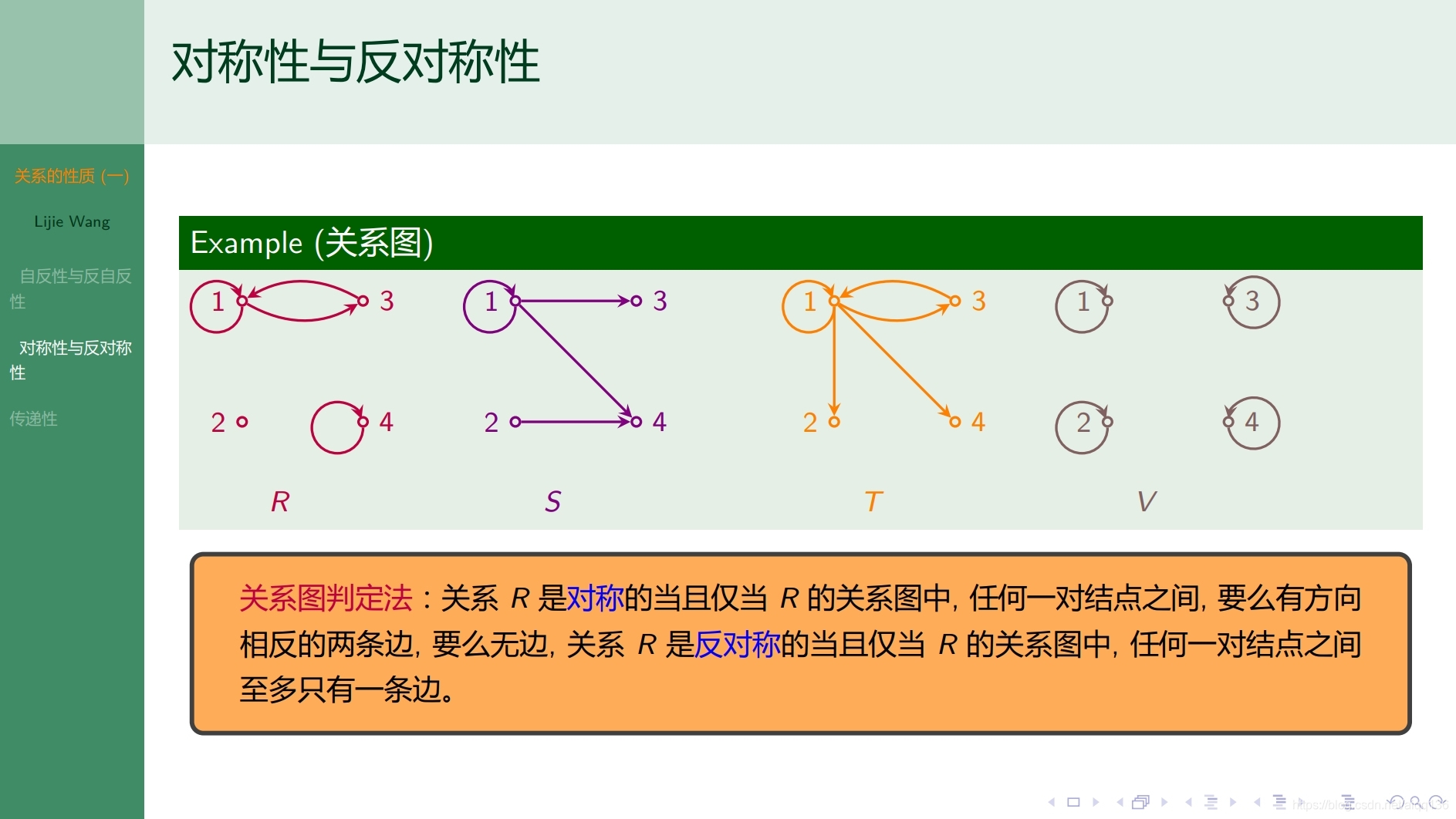
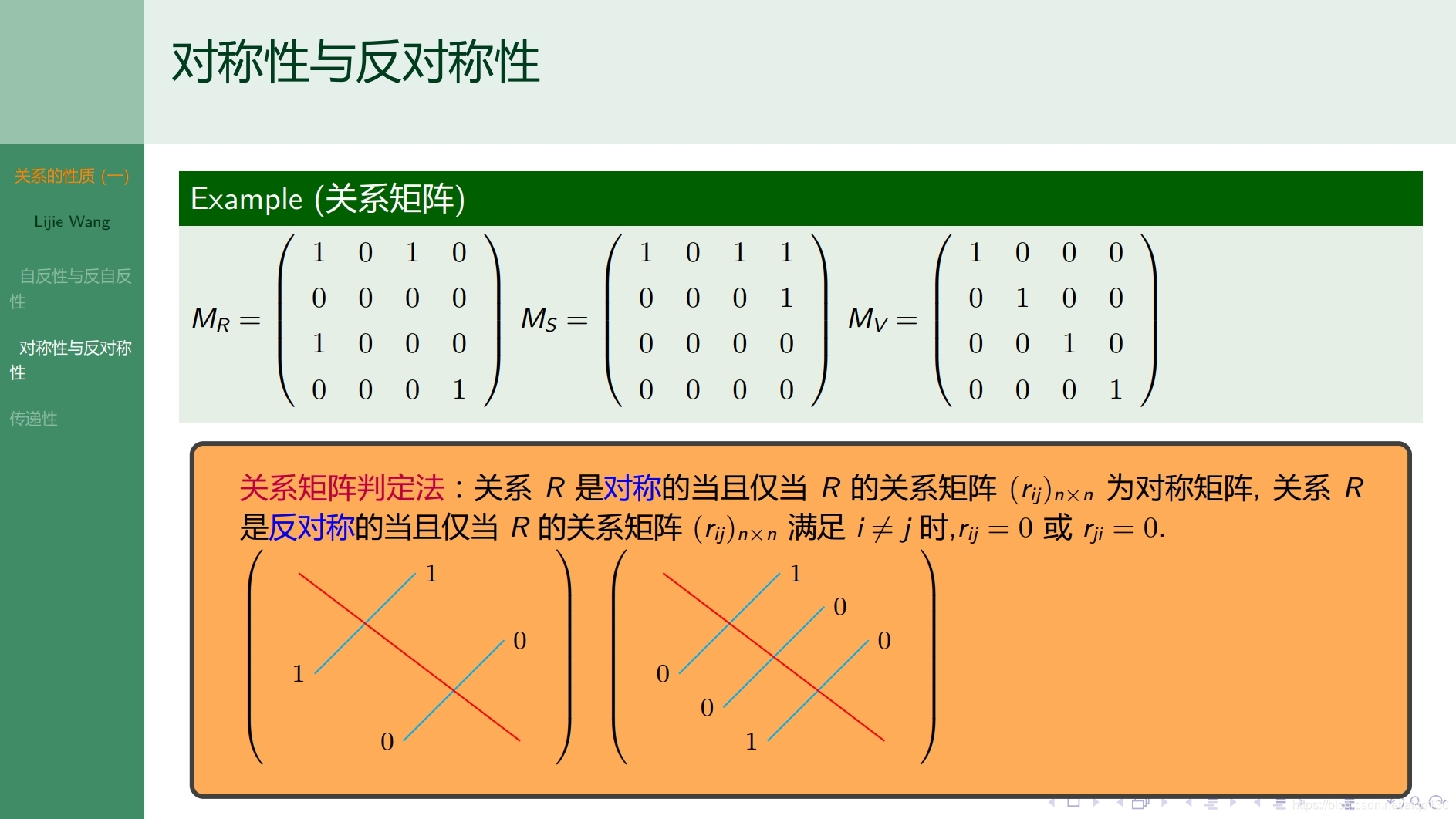
6.8.1二元关系 关系的性质（二）

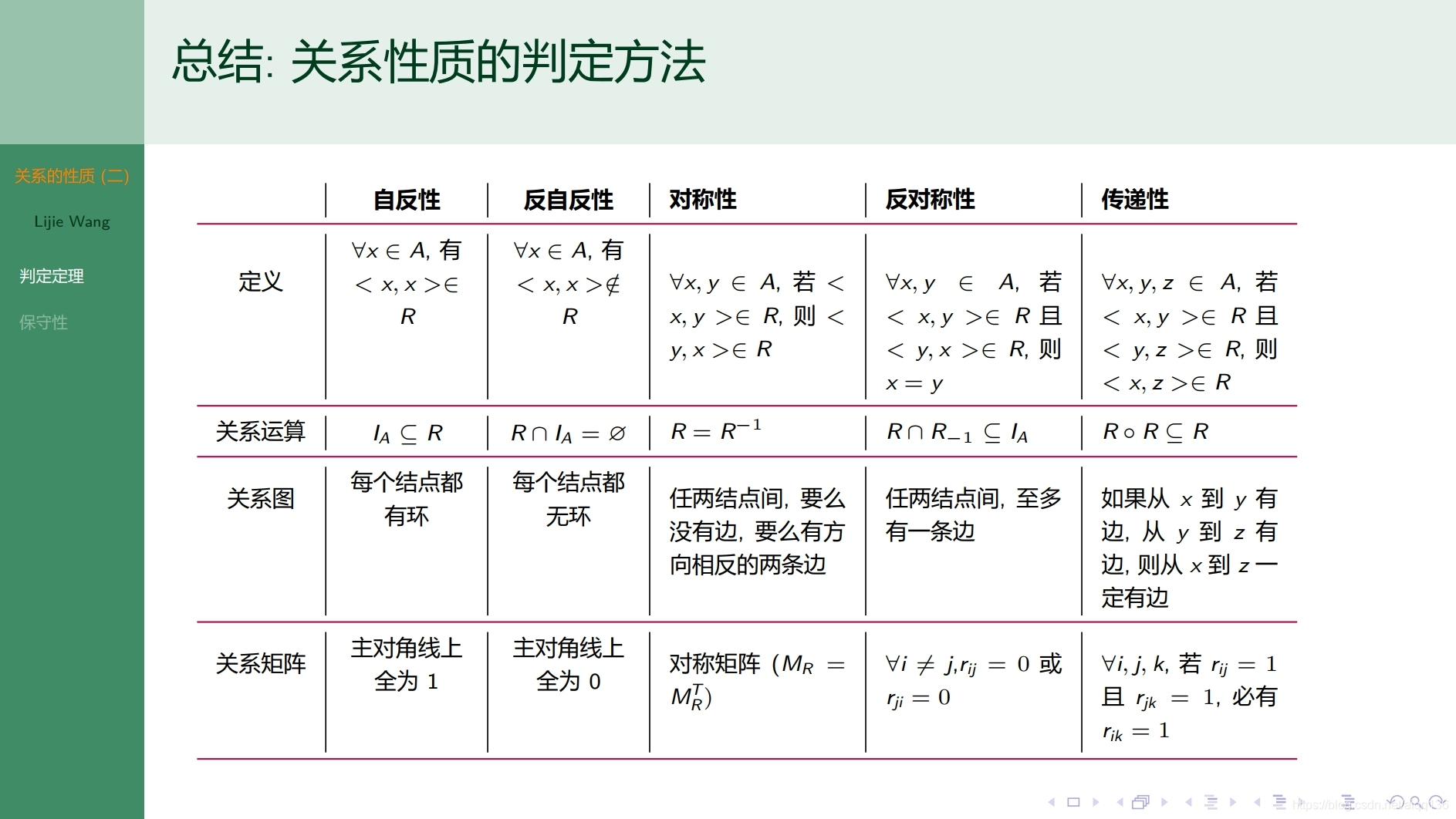
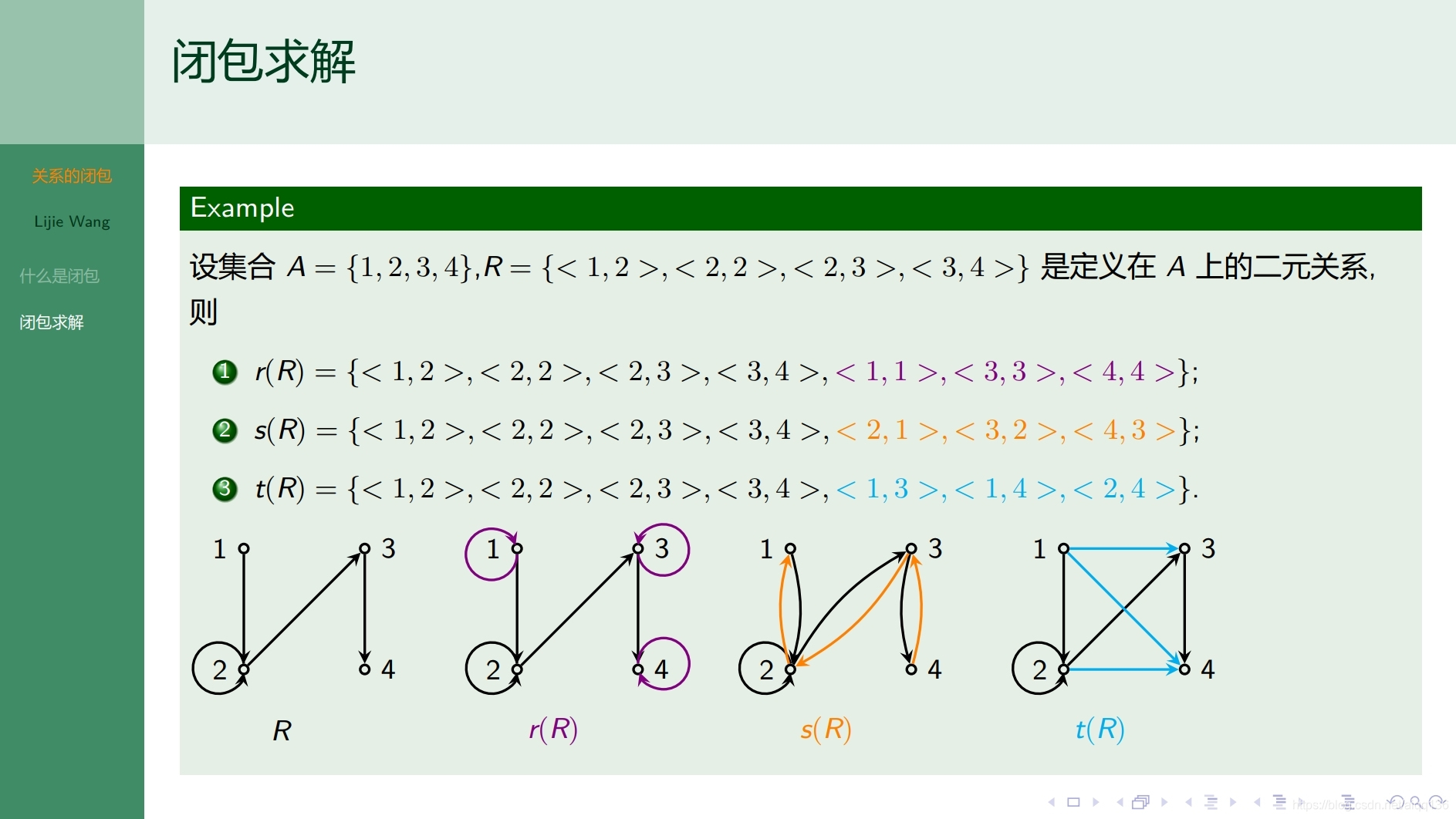
6.9.1二元关系 关系的闭包

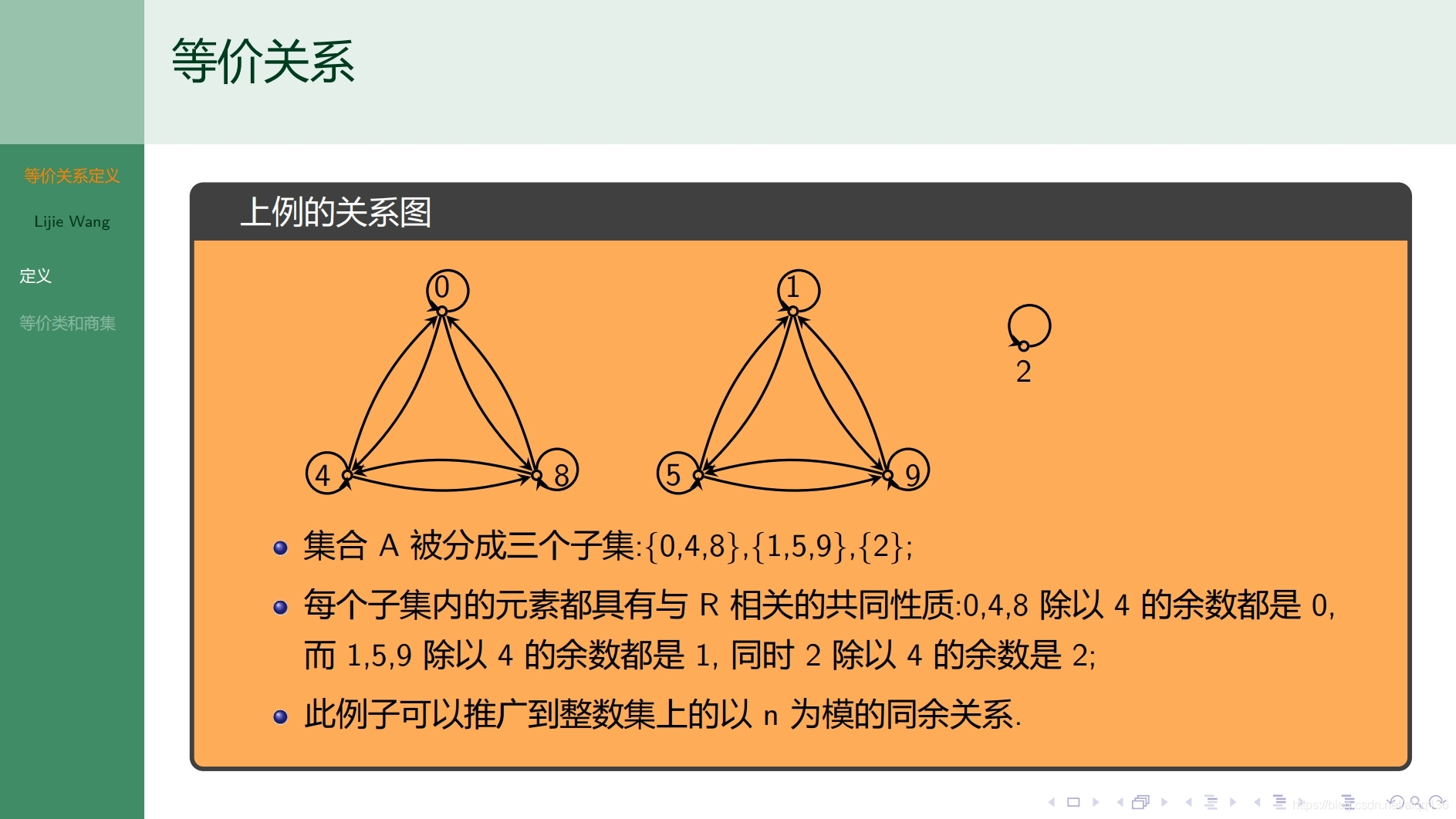
7.1.1特殊关系 等价关系

7.2.1特殊关系 集合的划分

7.3.1特殊关系 偏序关系的定义

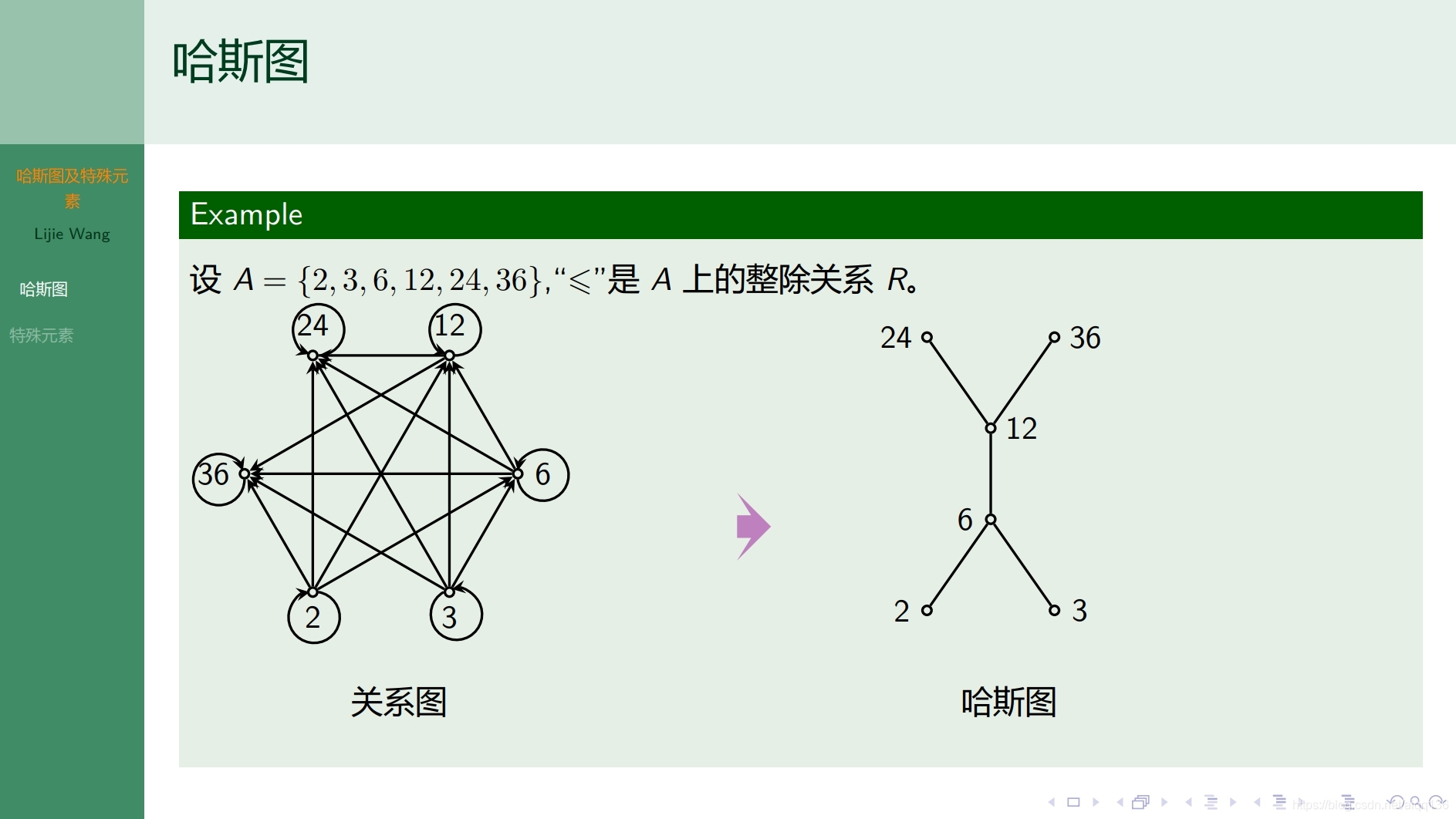
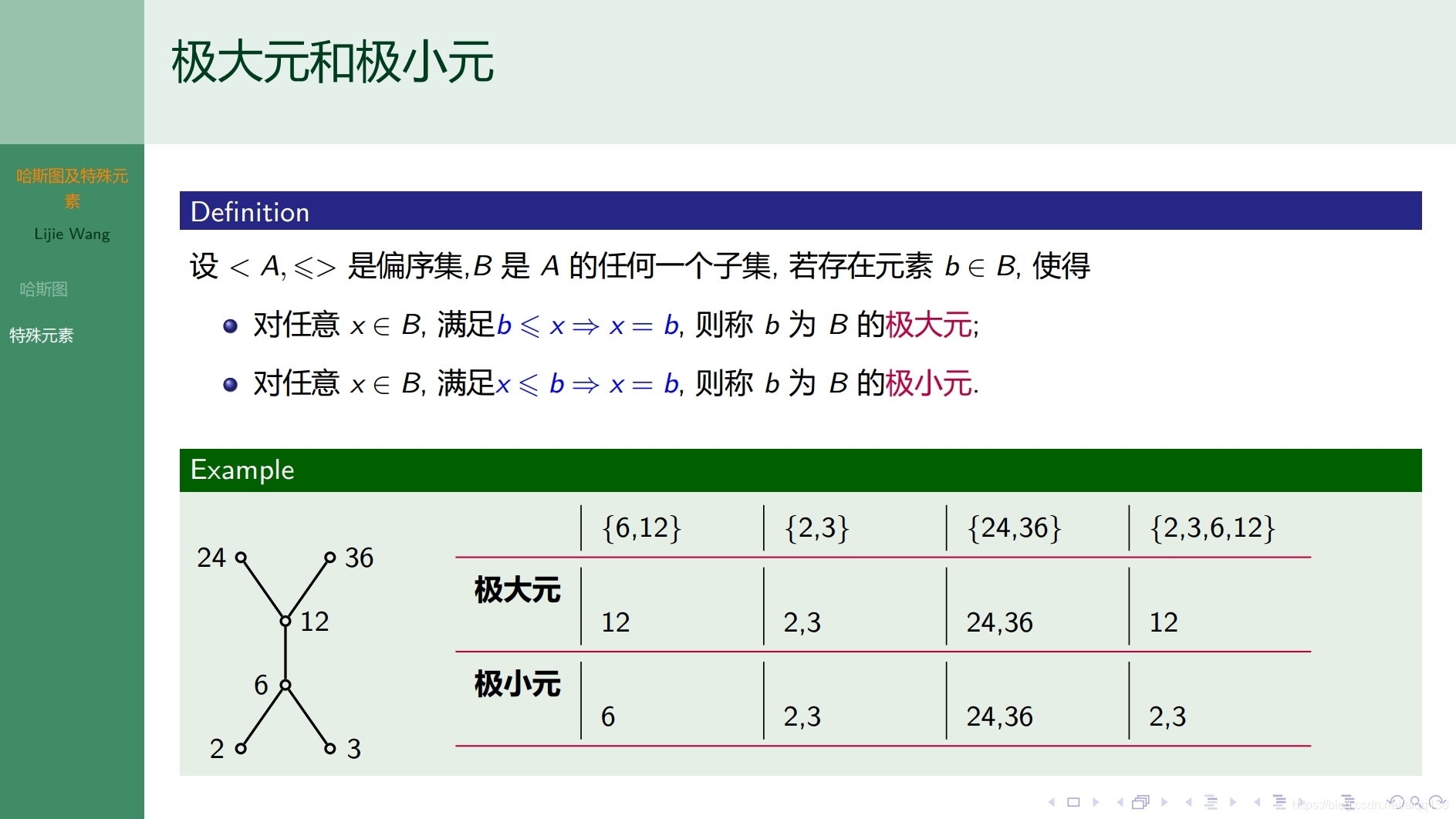
7.4.1特殊关系 哈斯图和特殊元素

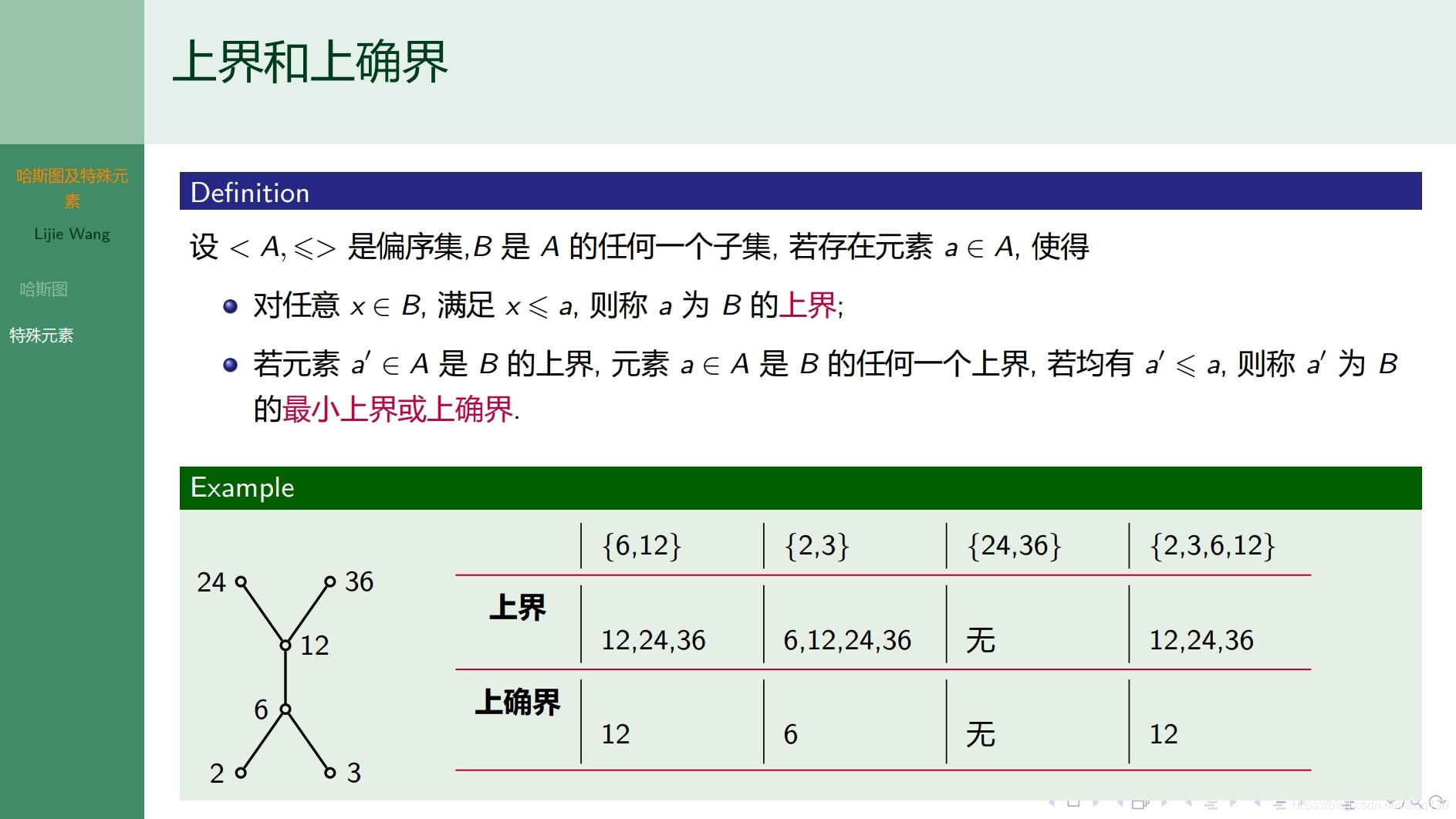
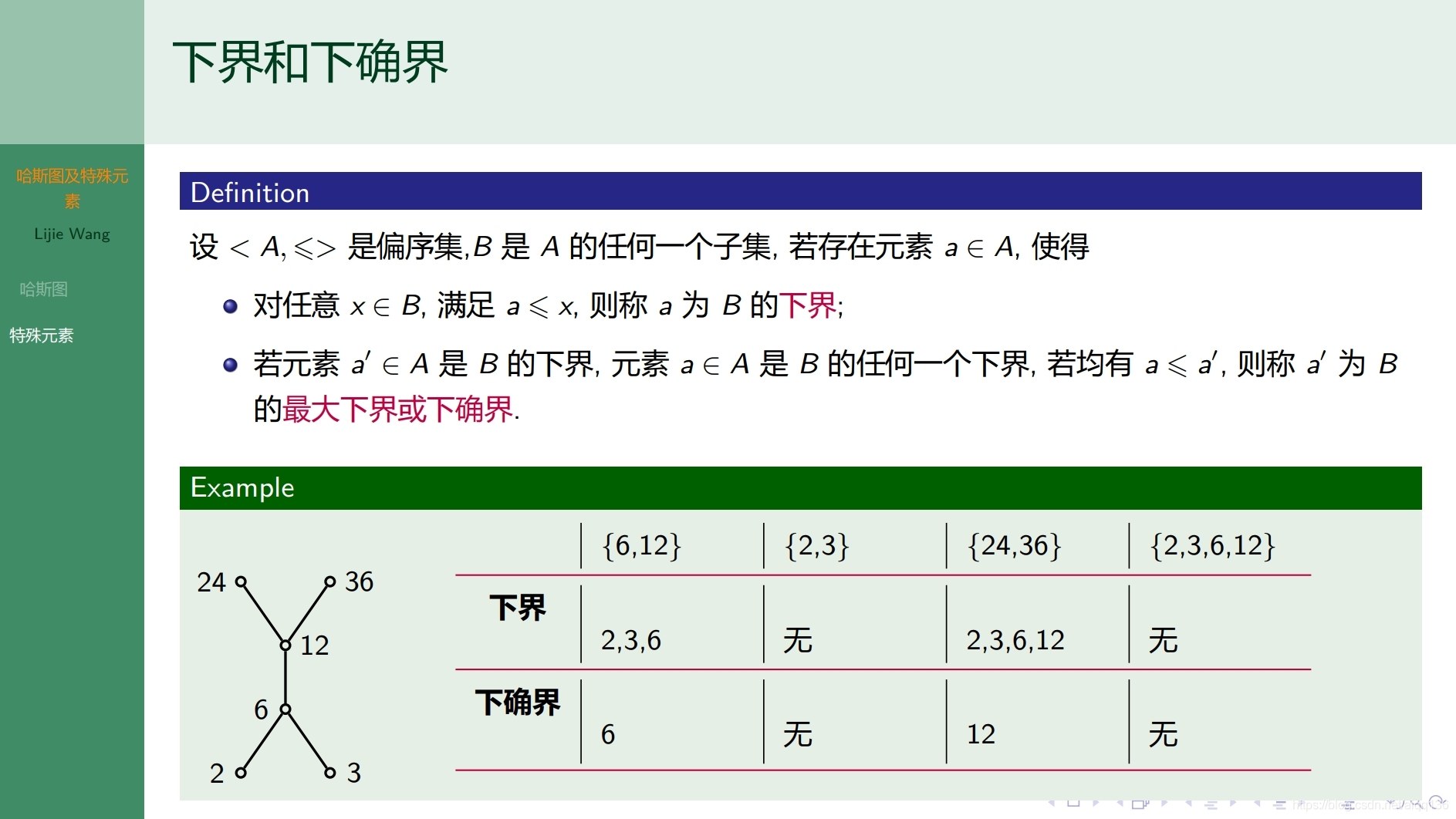
7.5.1特殊关系 其他次序关系

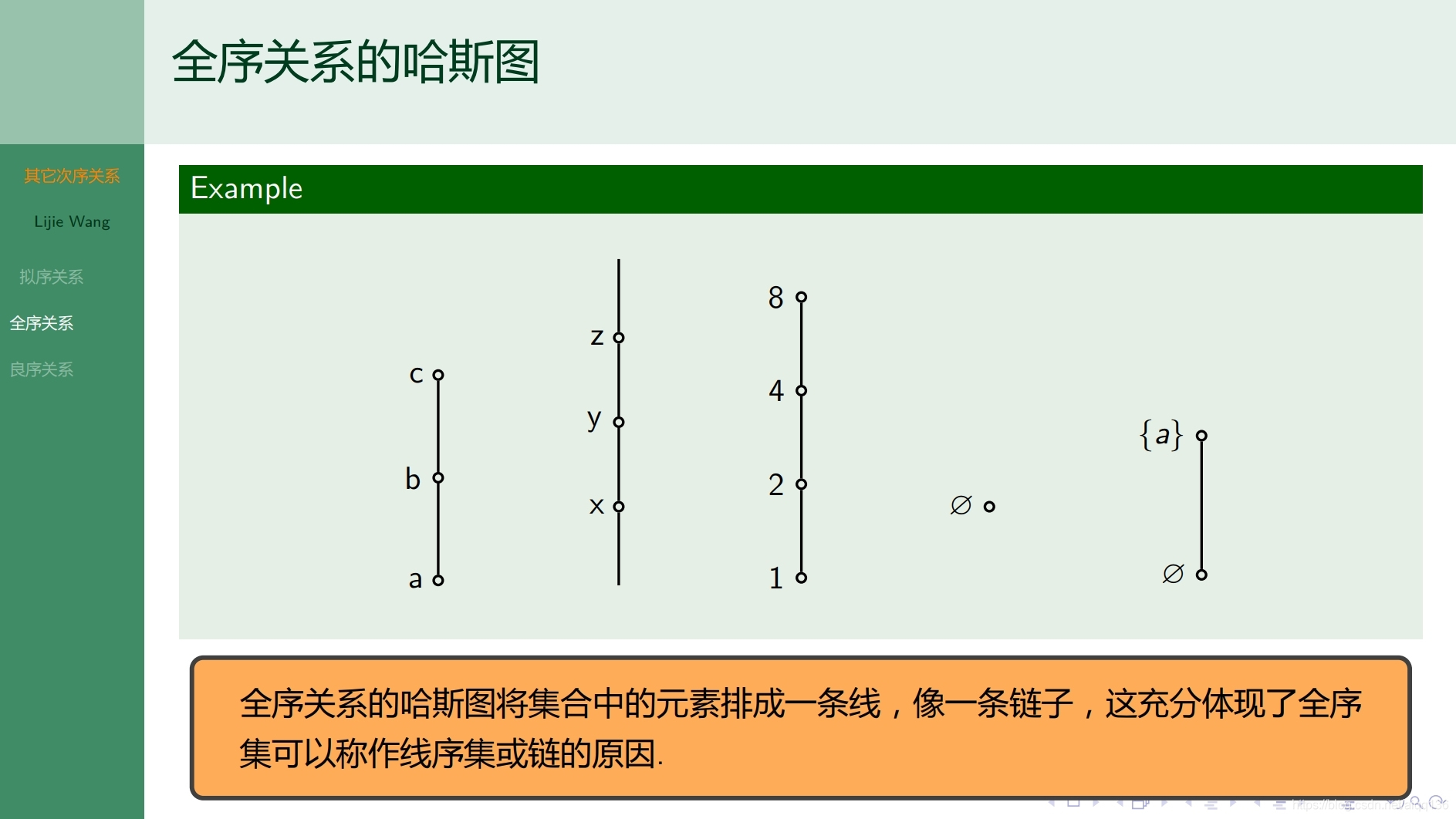
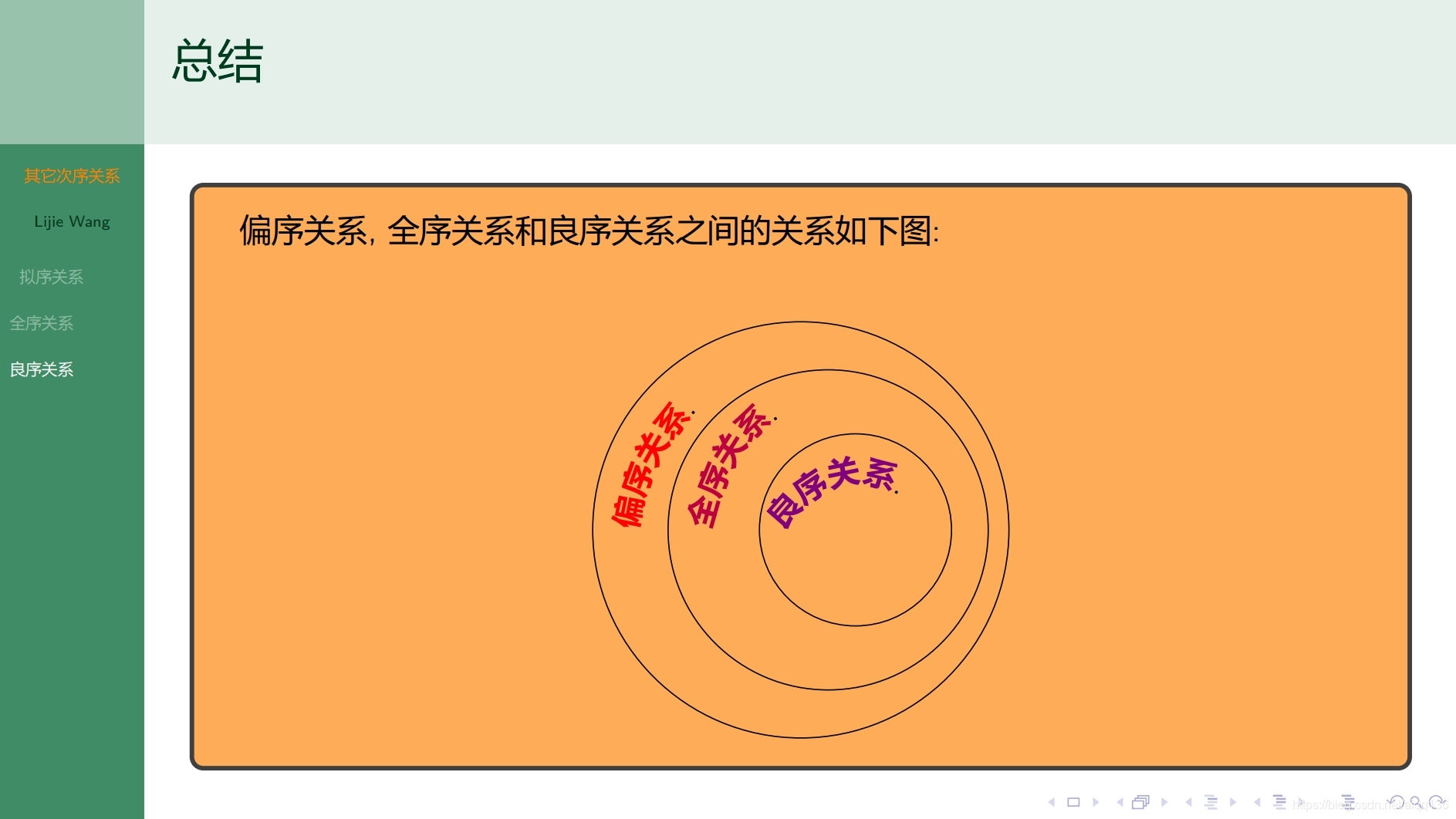
7.6.1函数 函数的定义

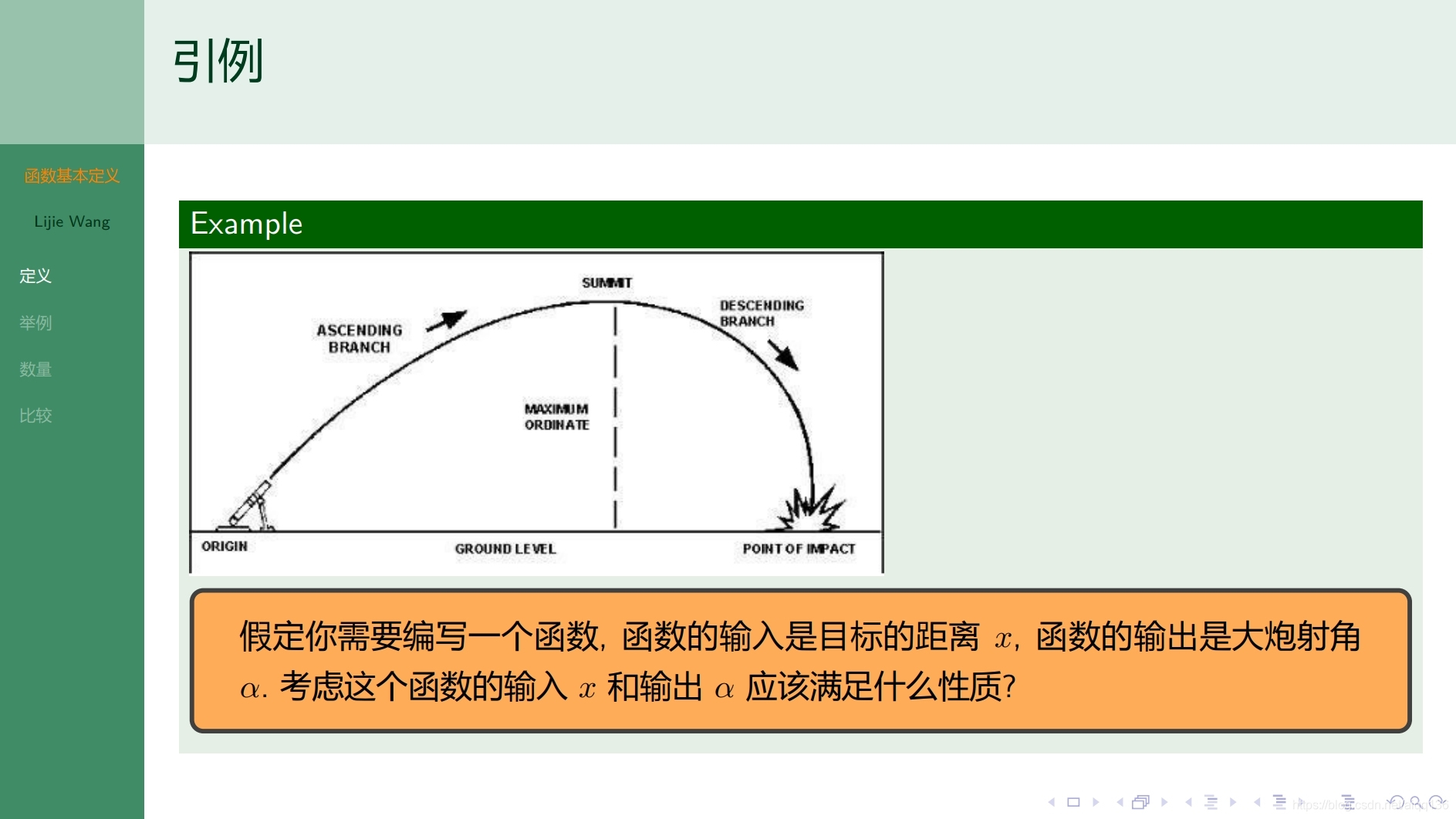
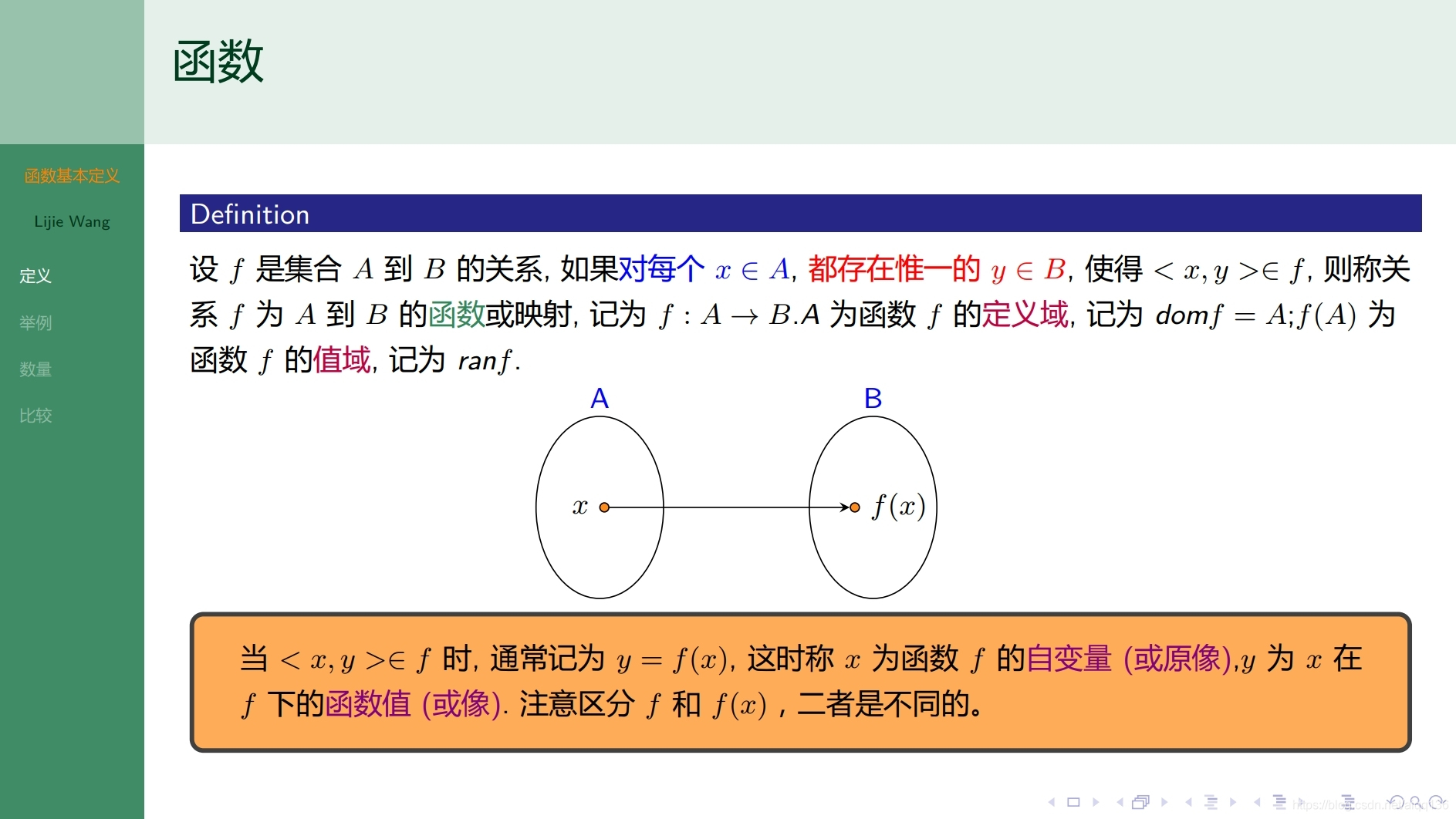
7.7.1函数 函数的类型

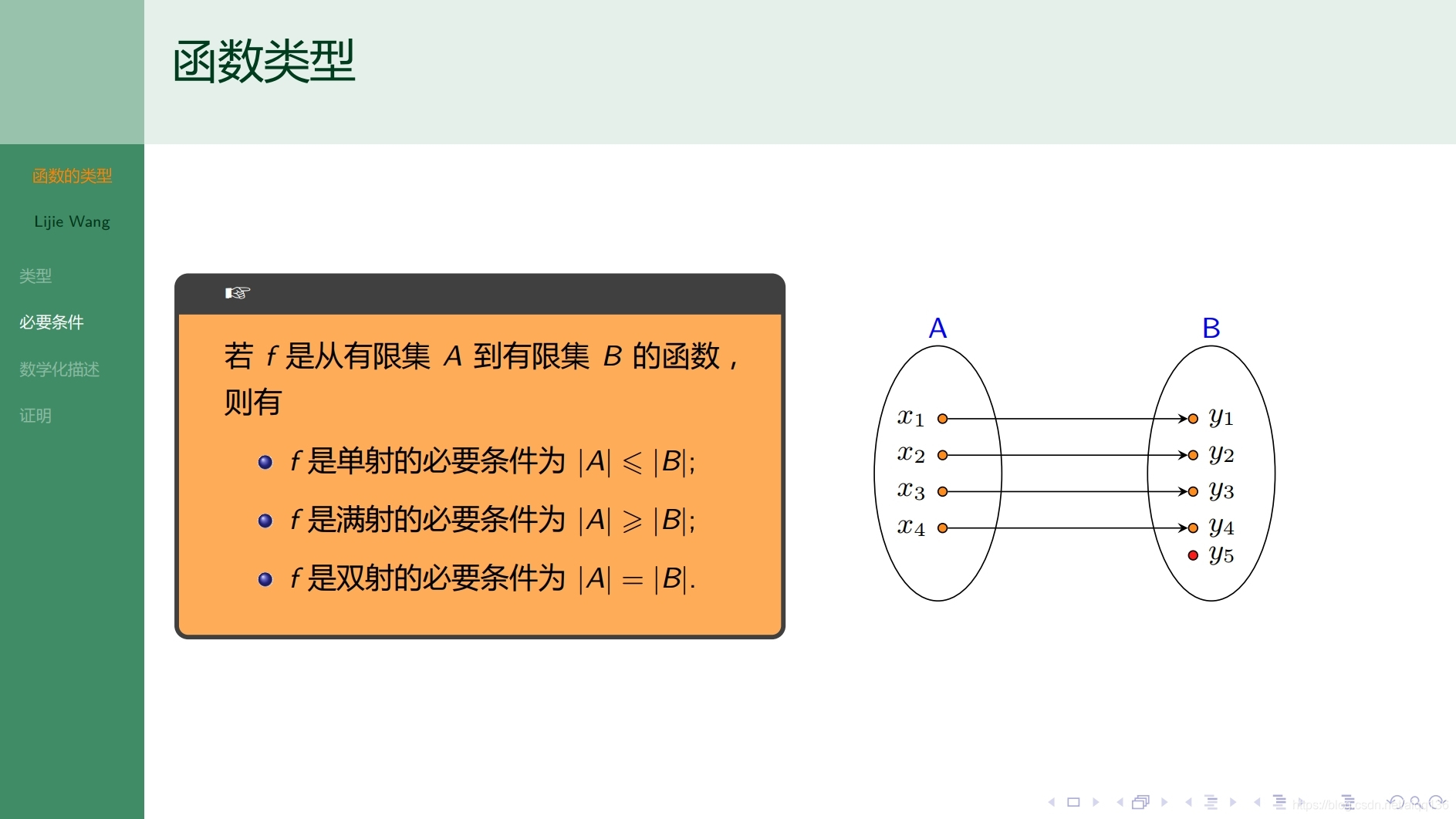
7.8.1函数 函数的运算

8.1.1图论基础 图的引入

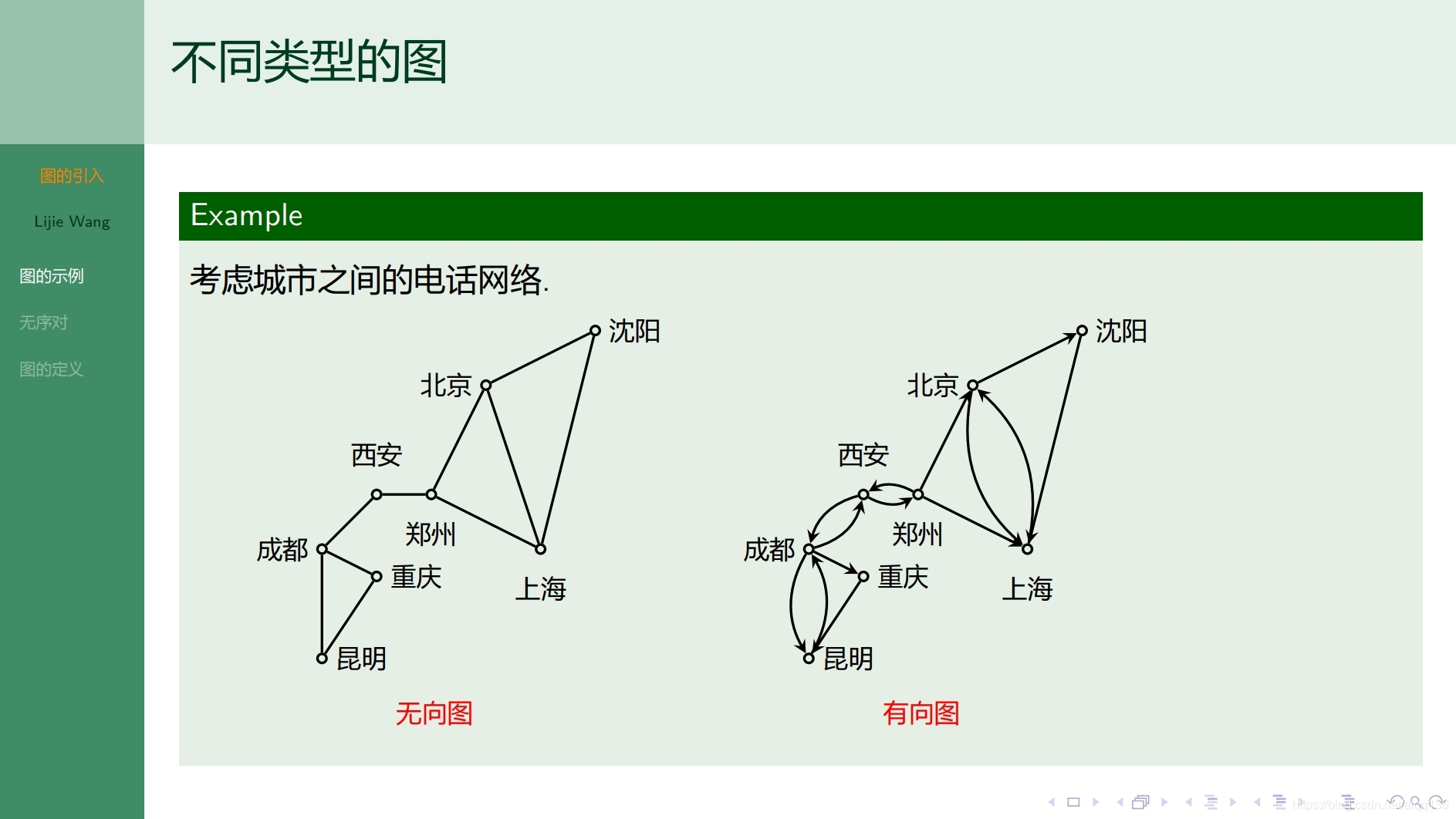
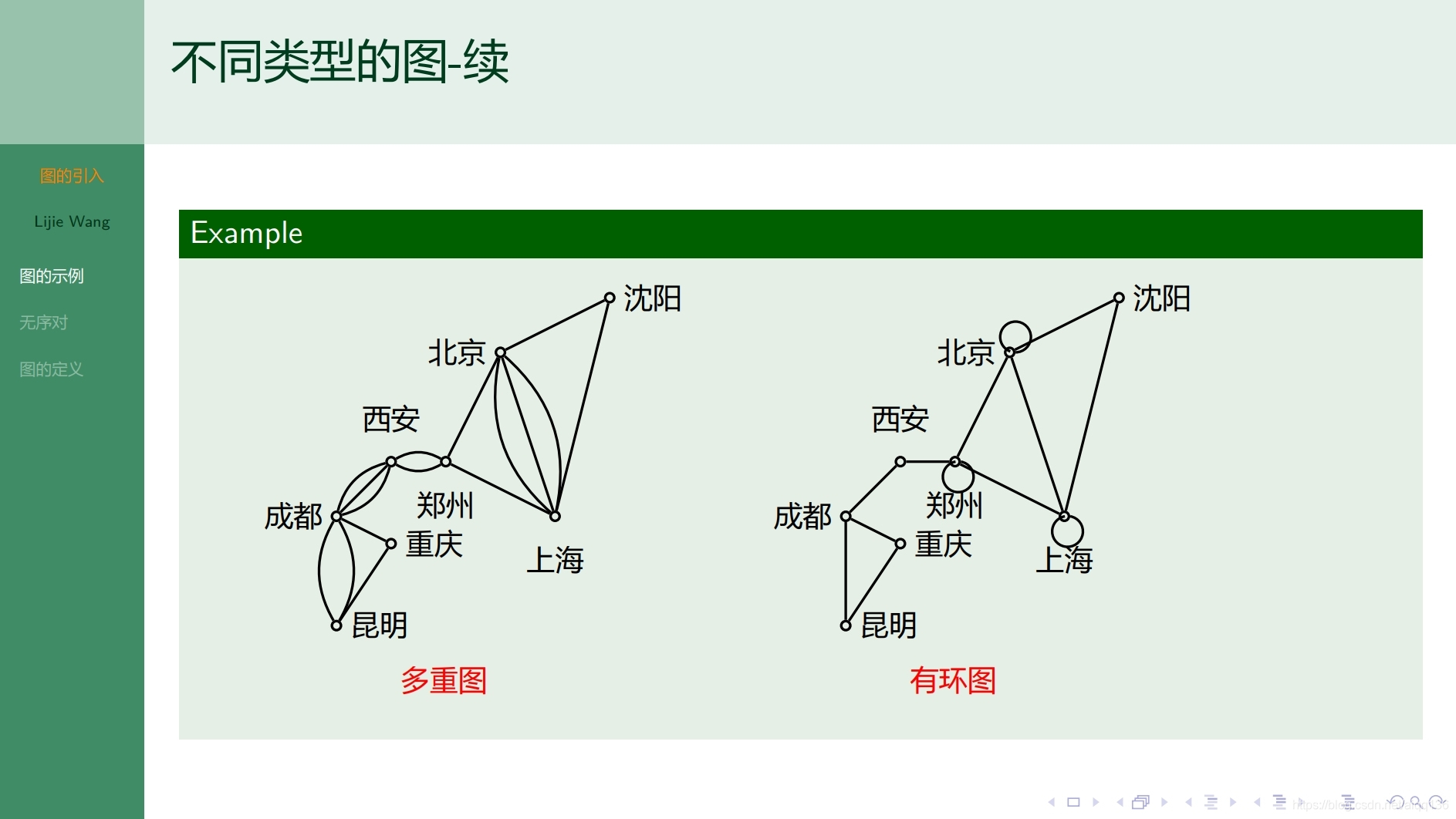
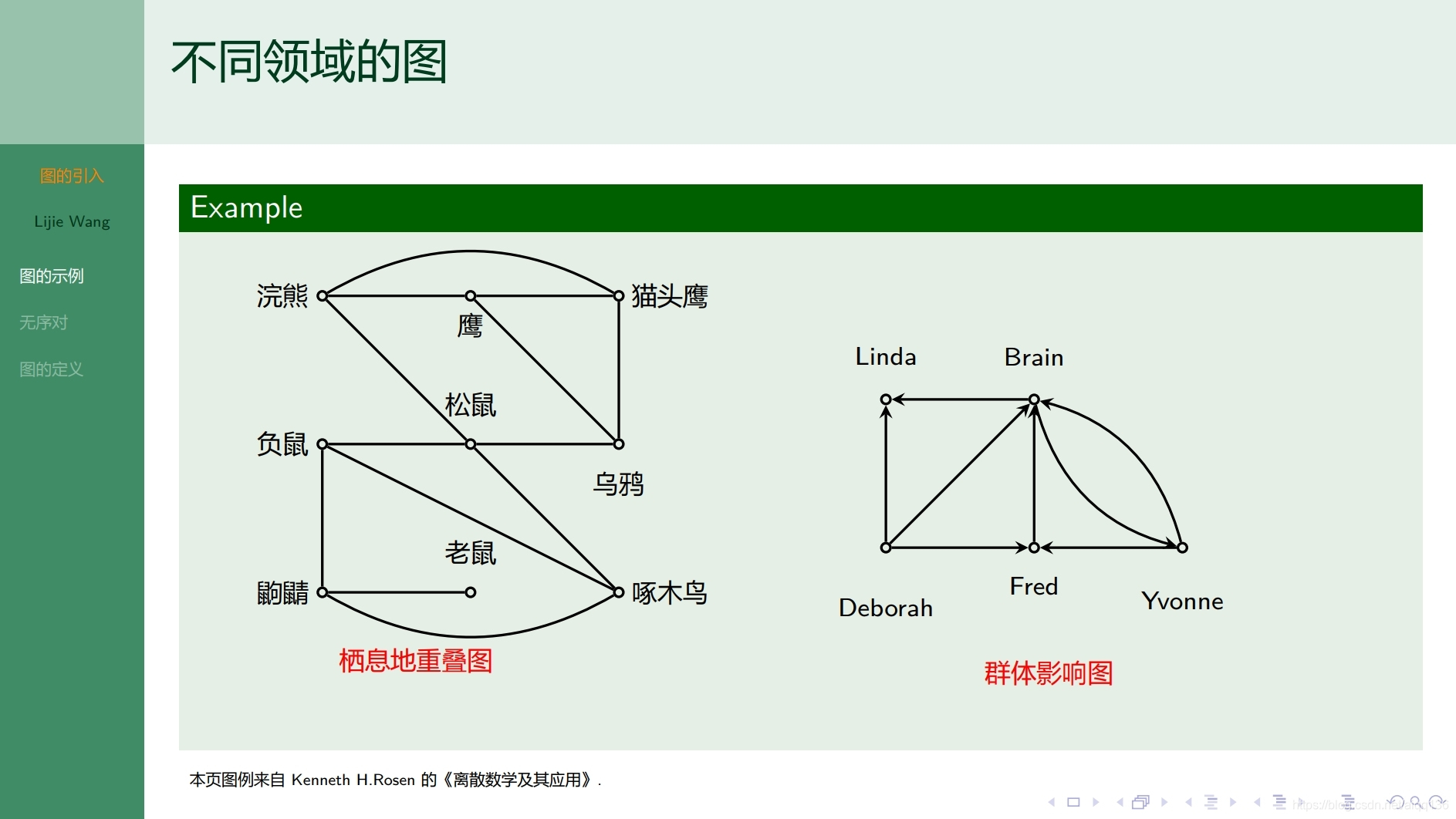
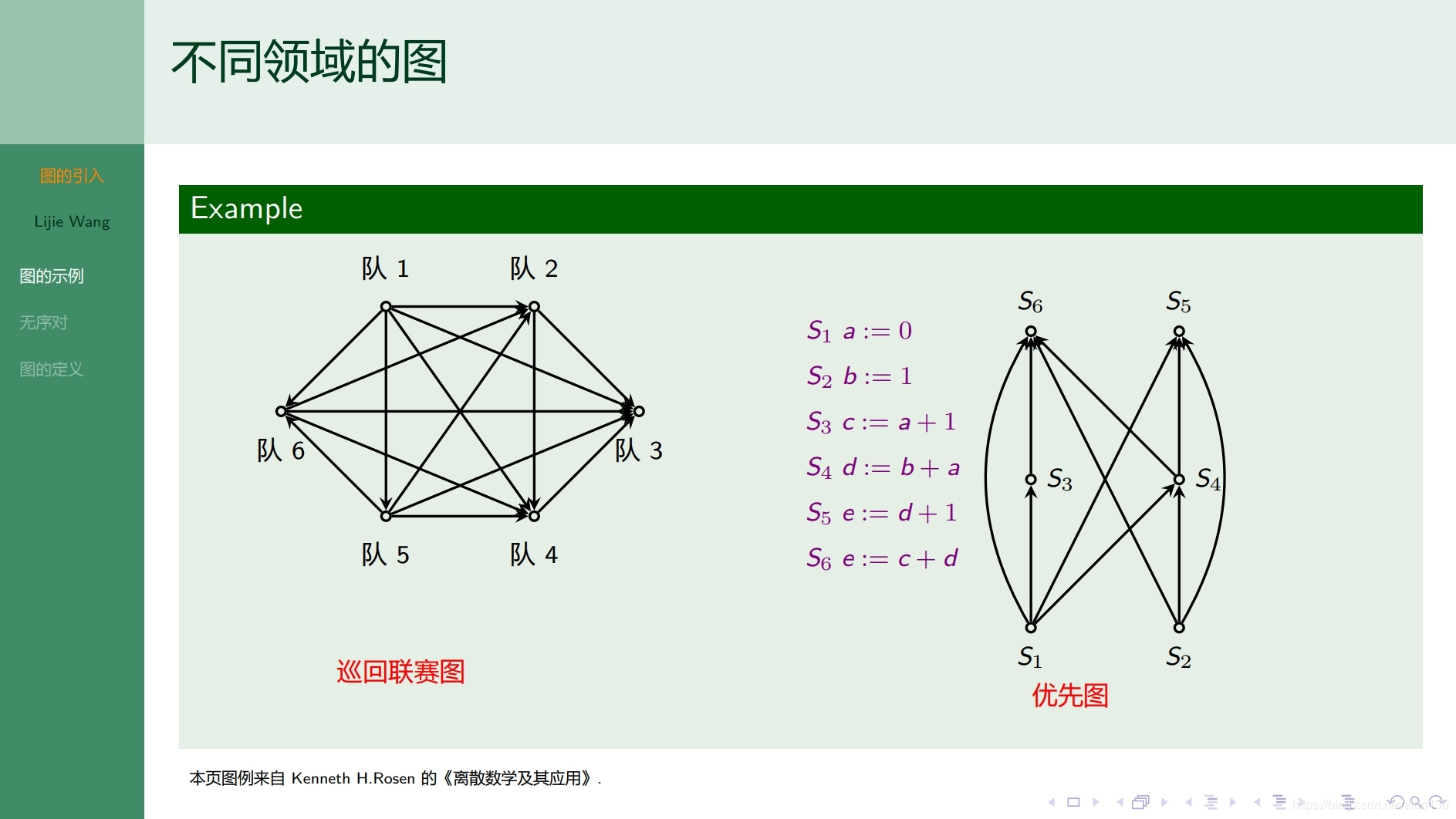
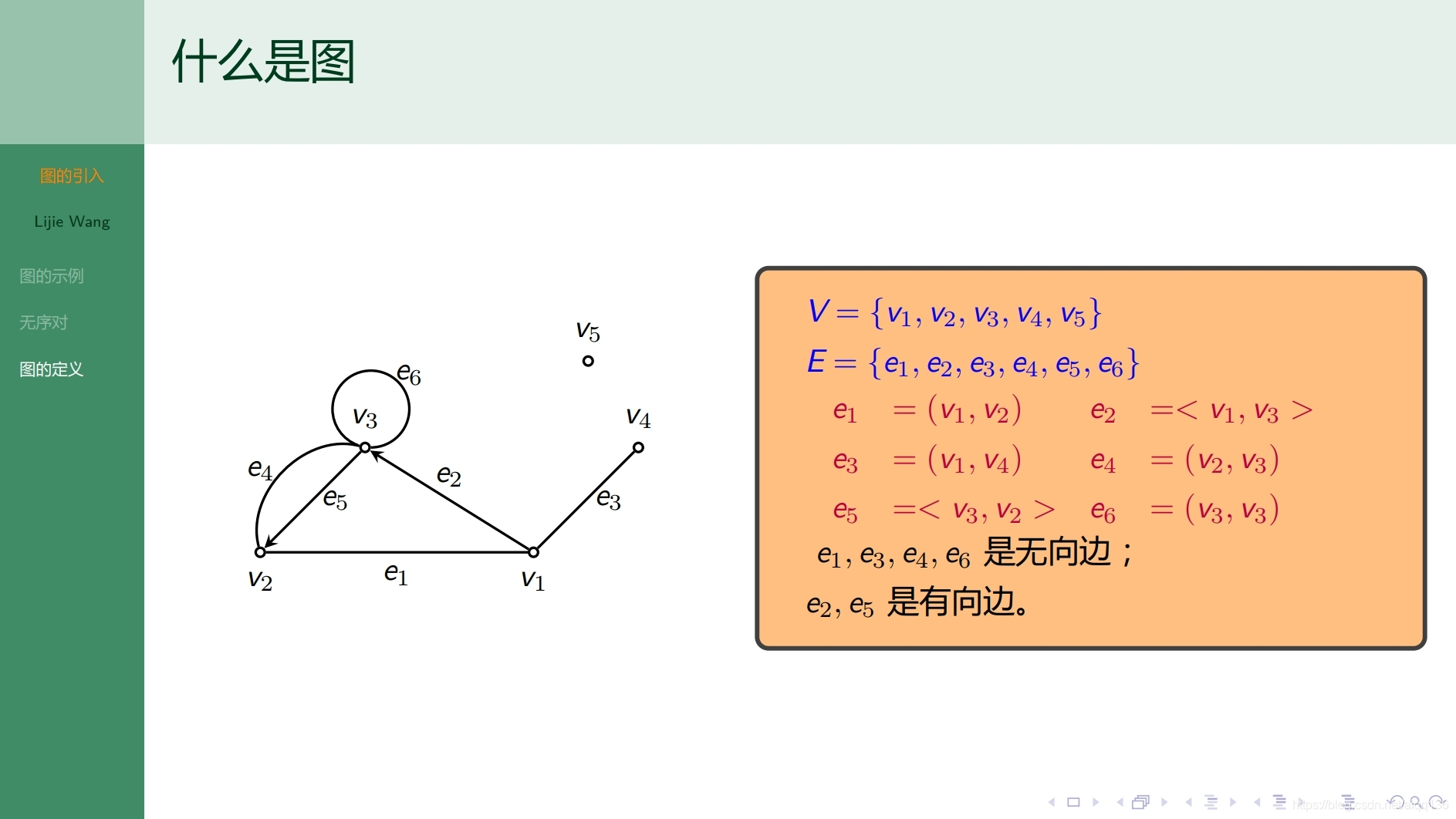
8.1.2图论基础 图的表示

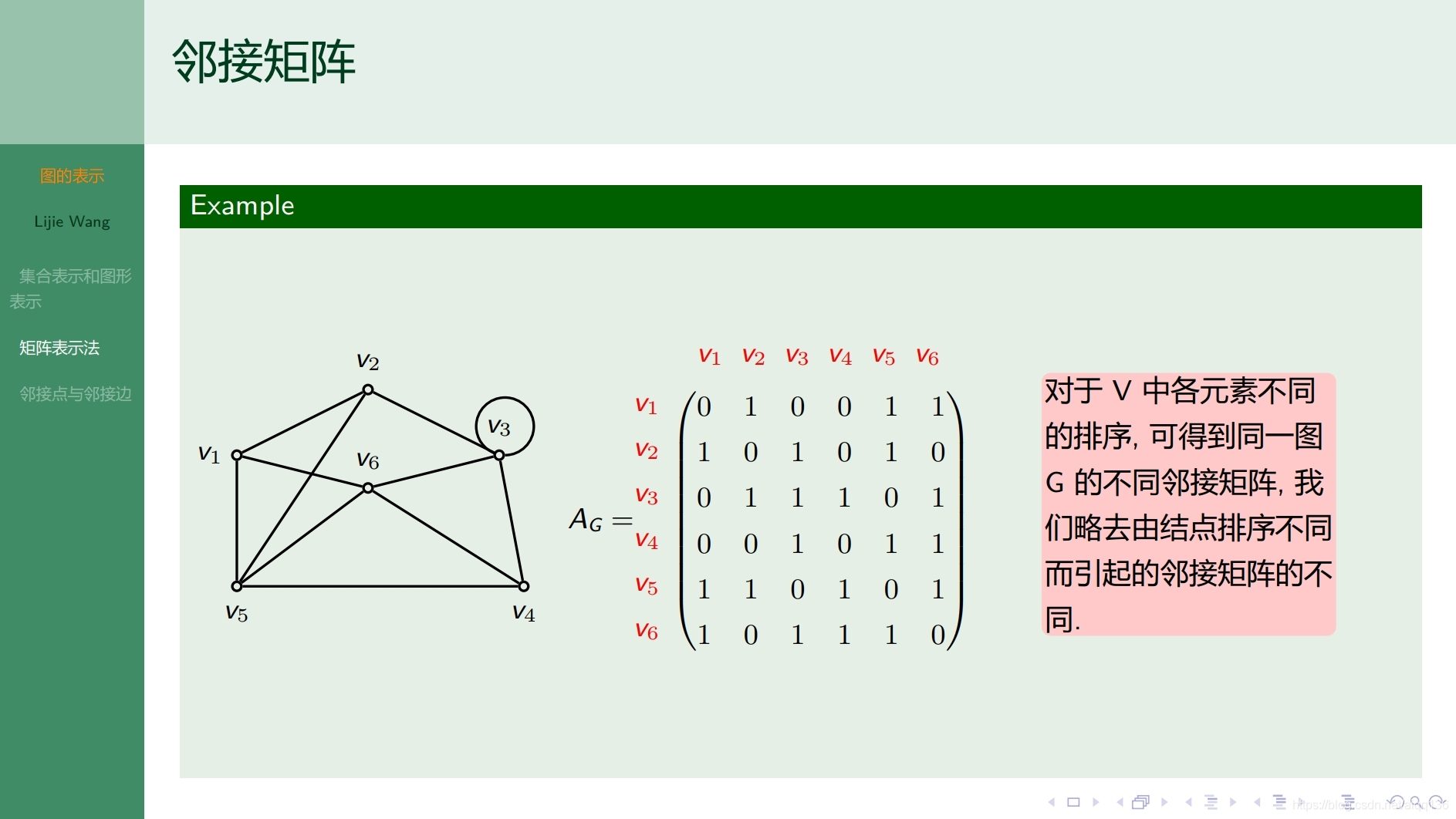
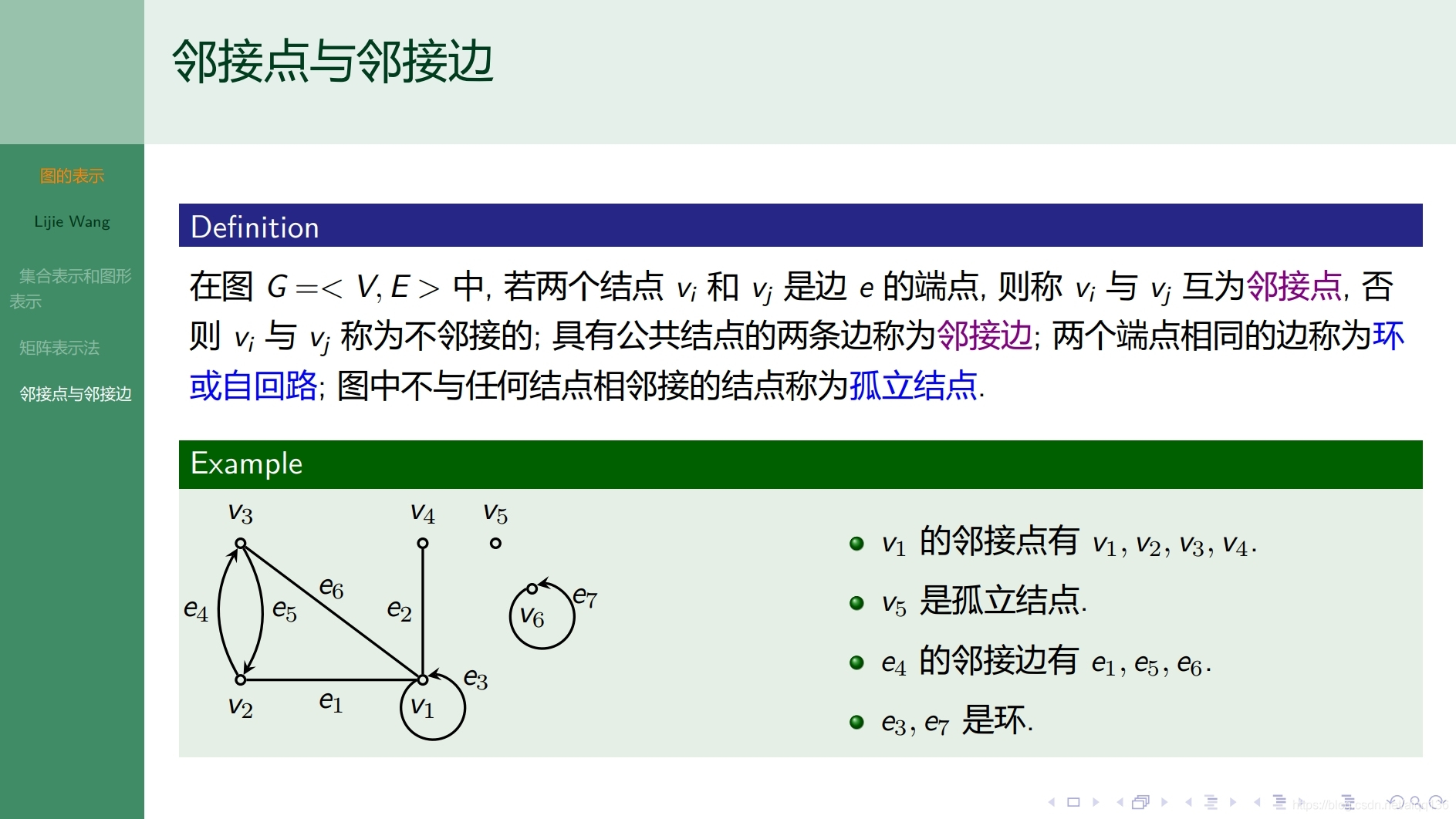
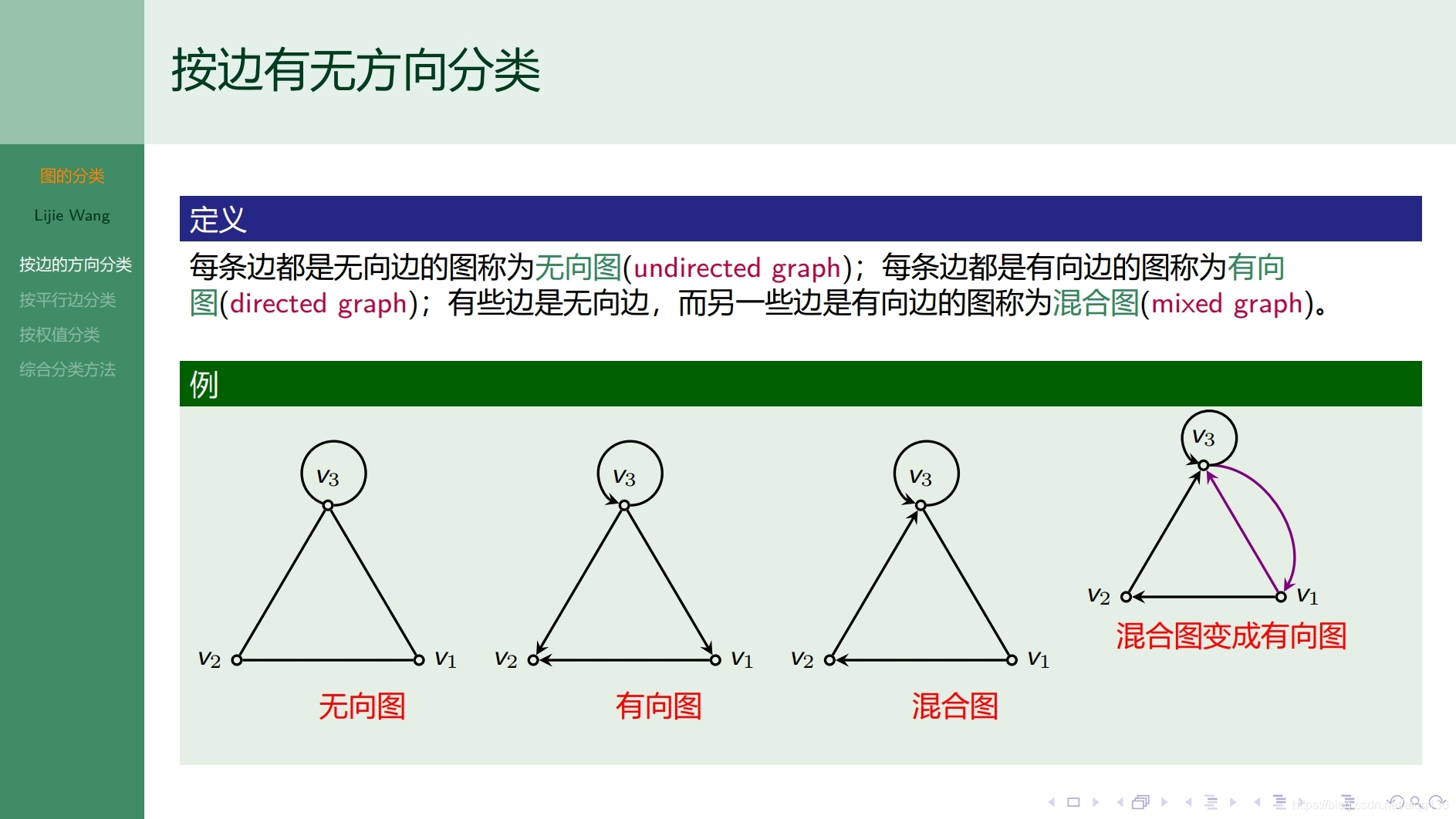
8.1.3图论基础 图的分类

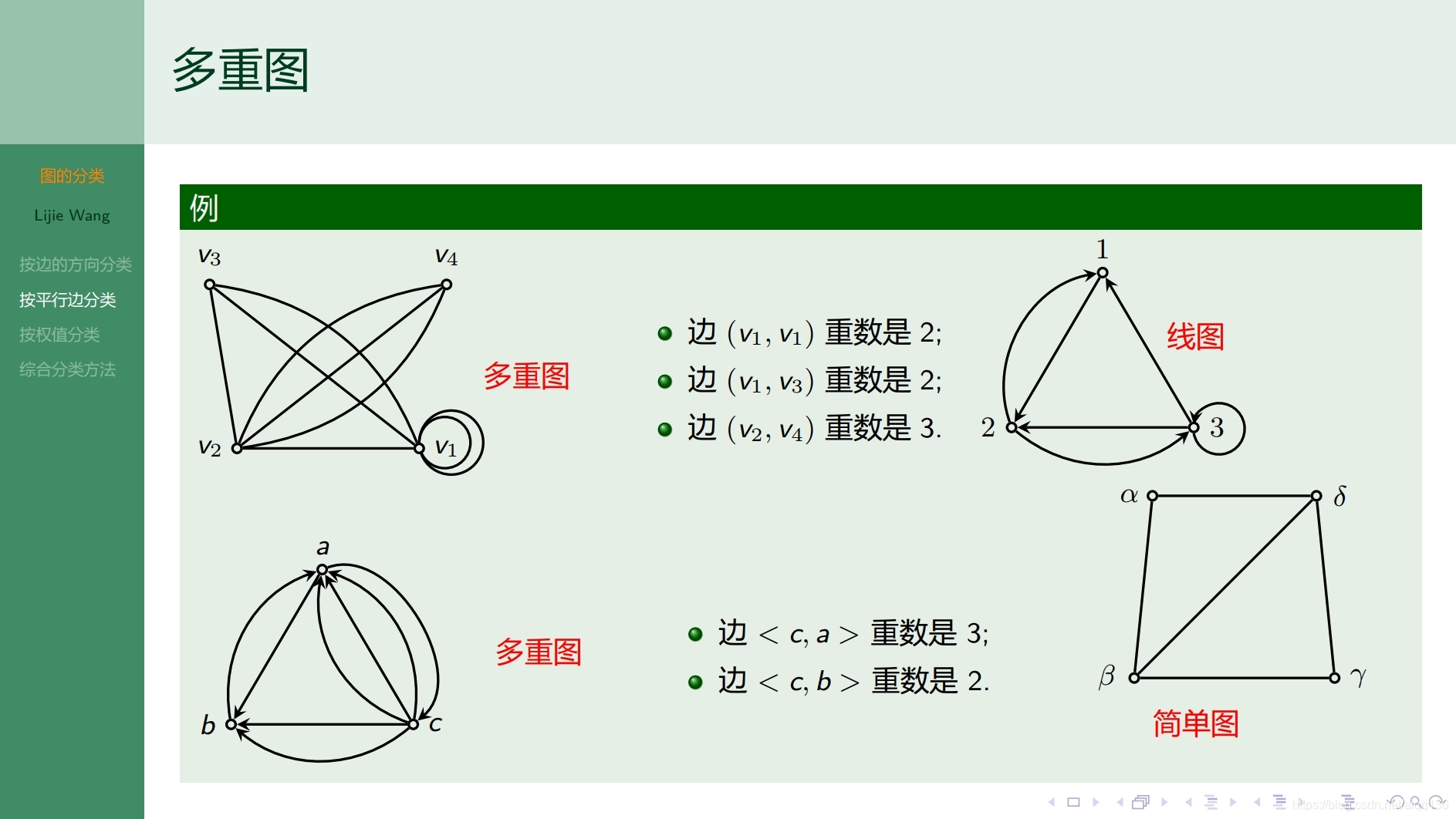
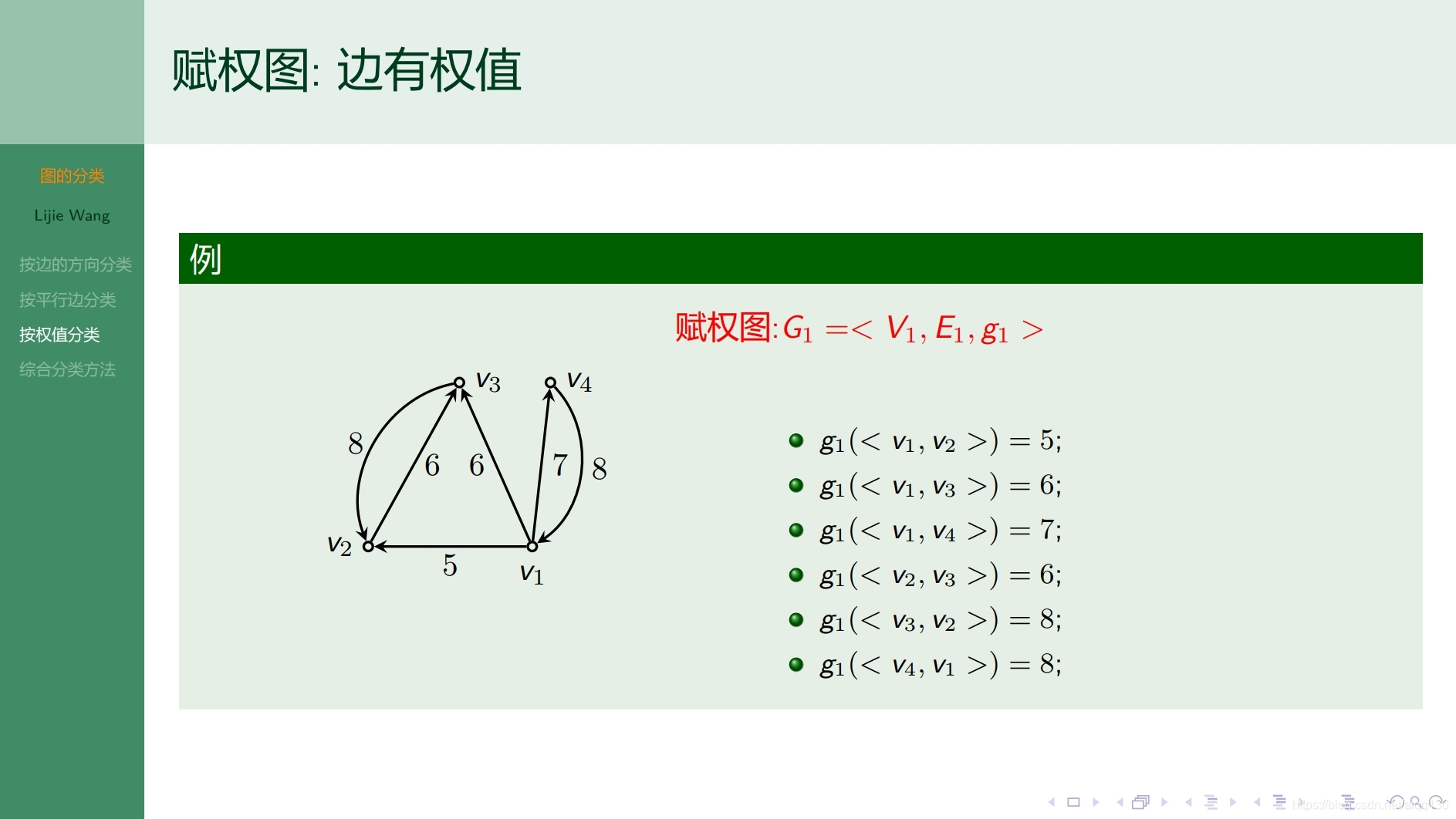
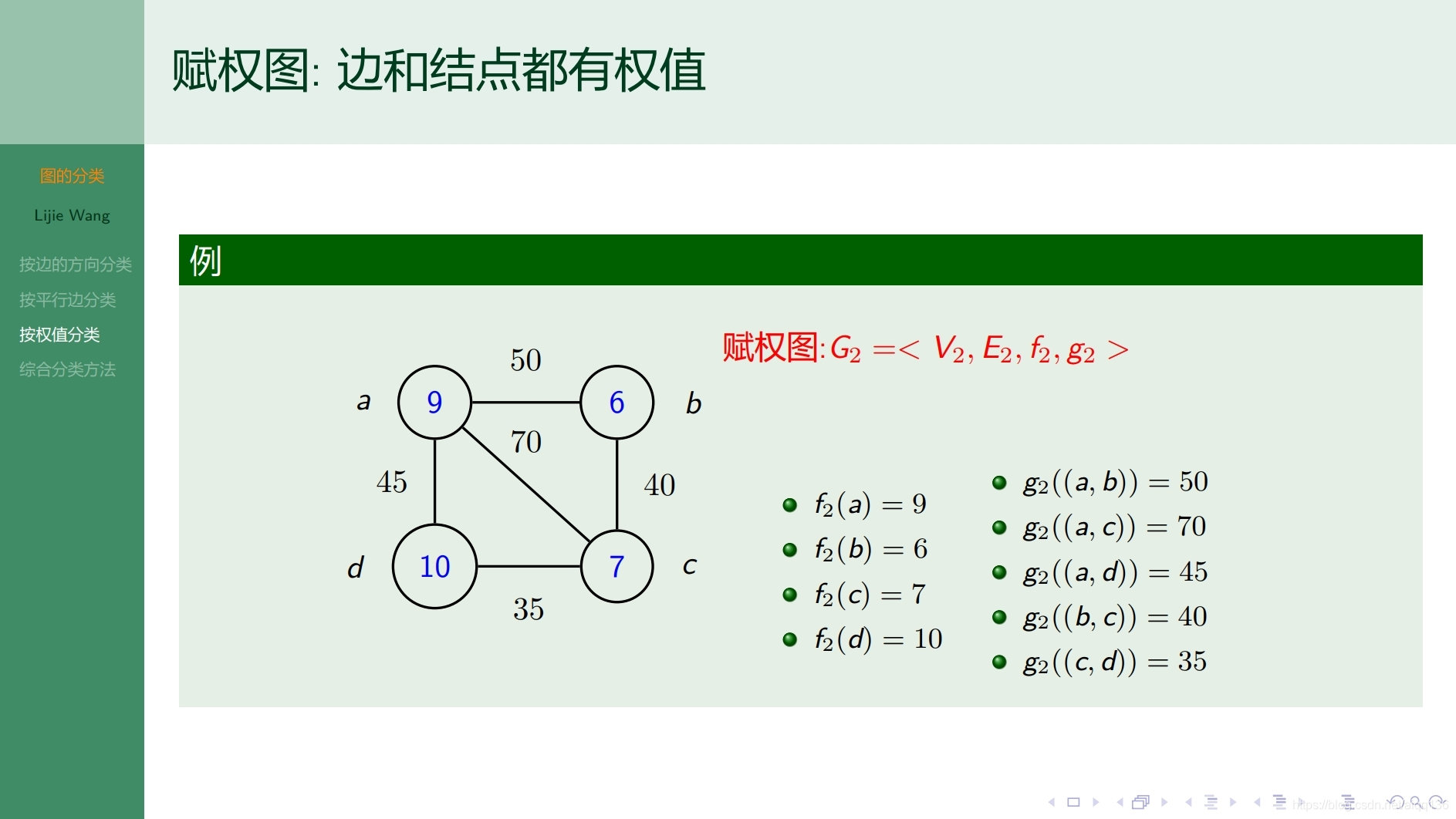
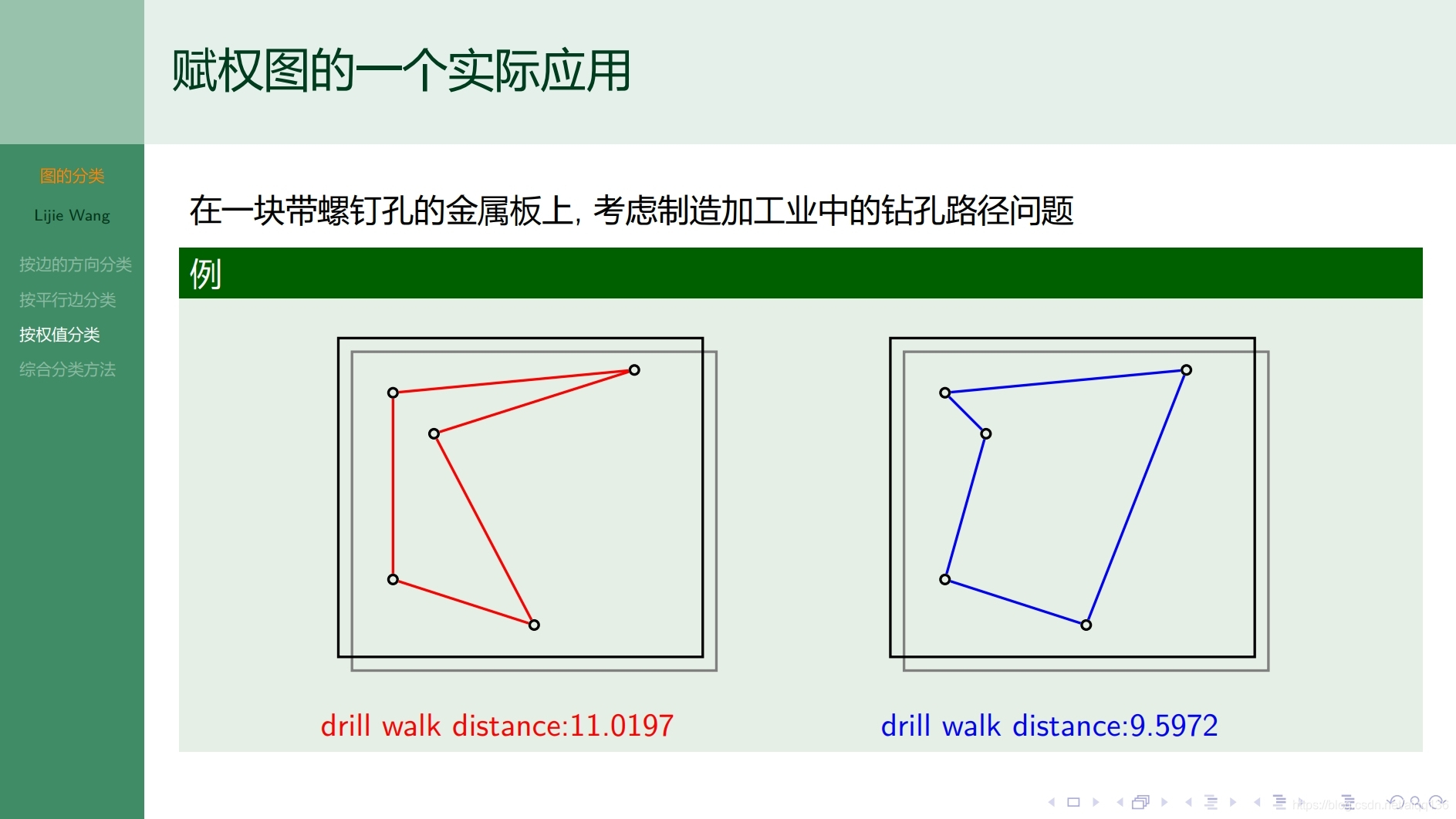
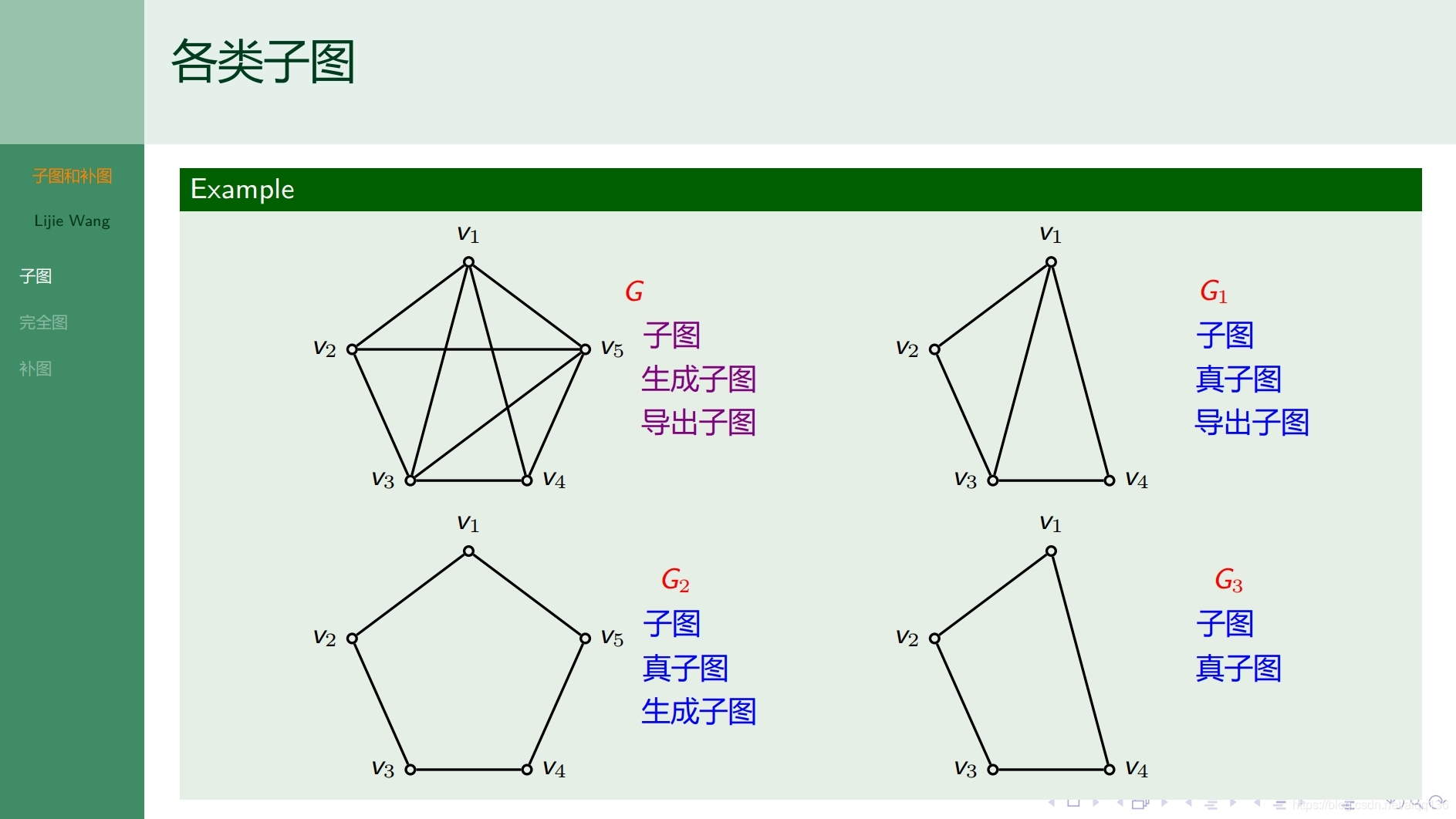
8.1.4图论基础 子图和补图

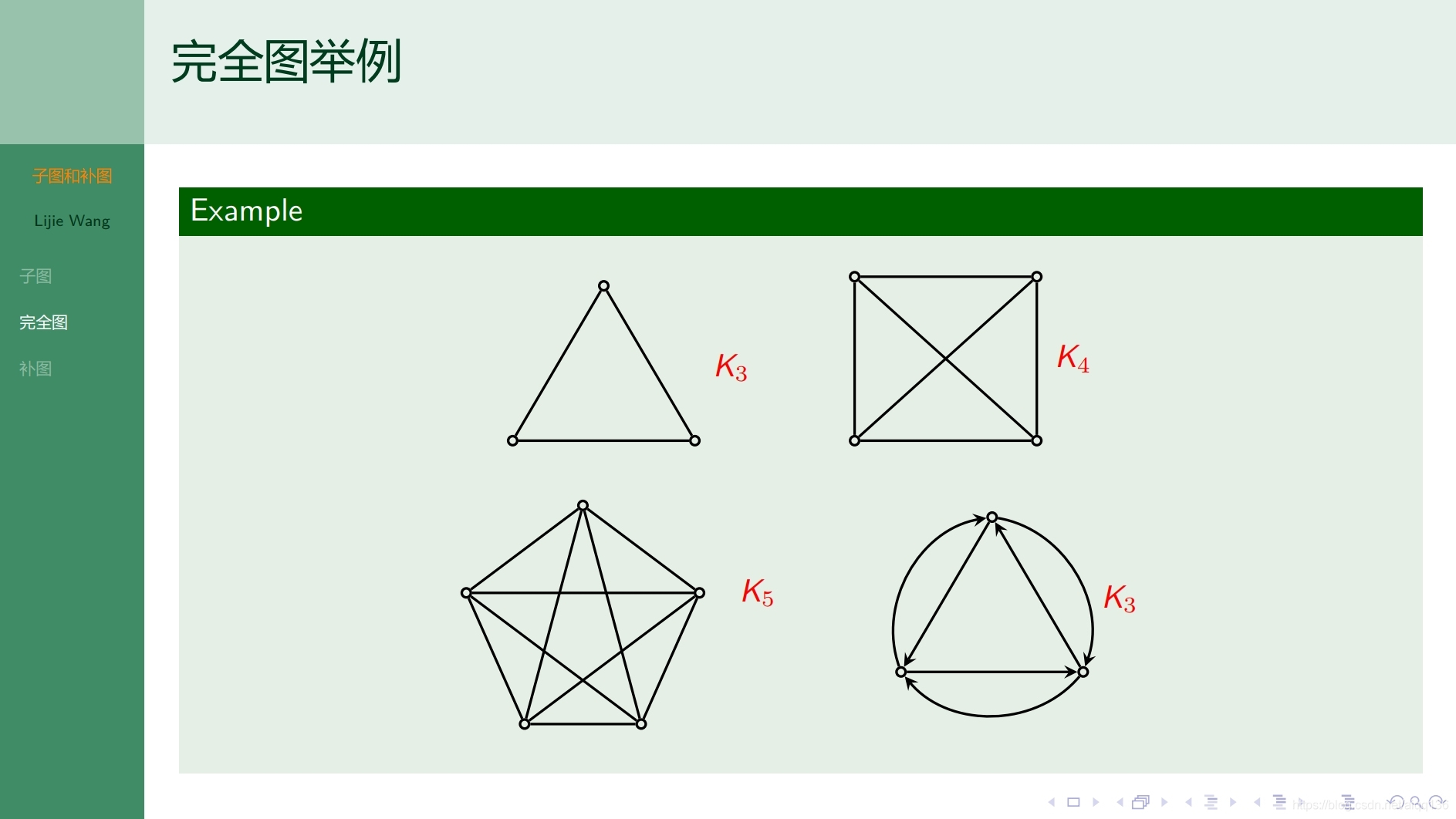
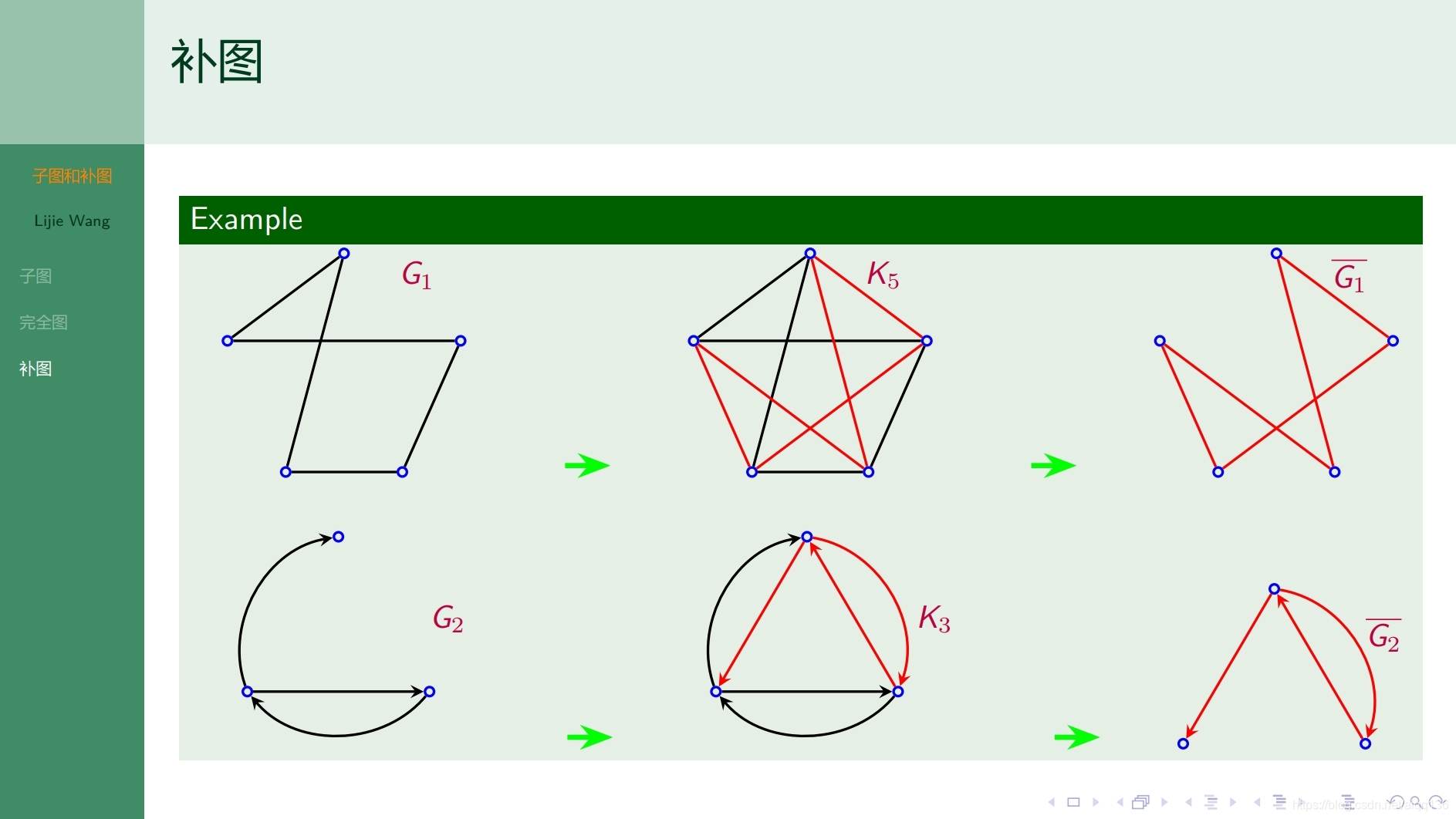
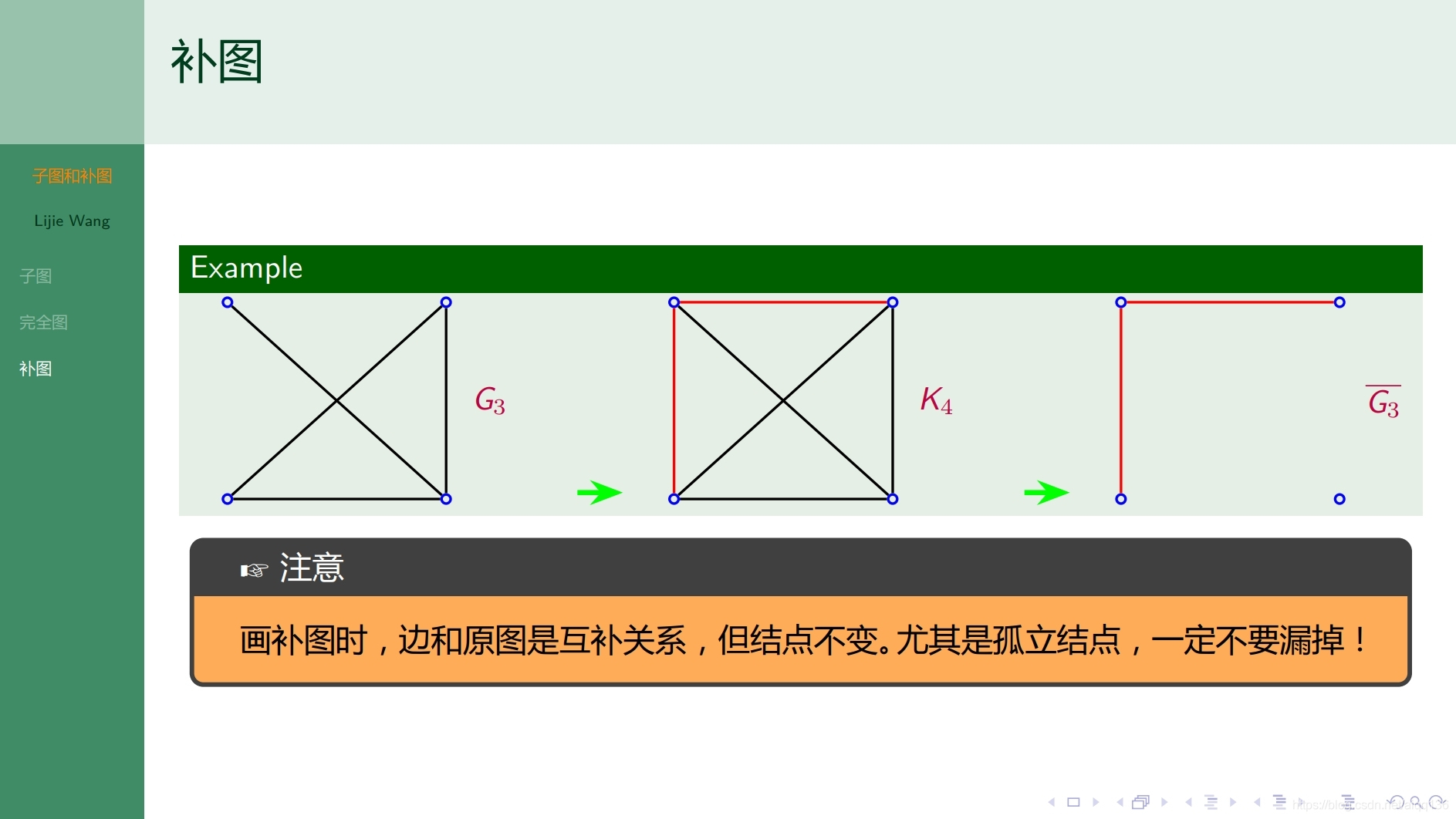
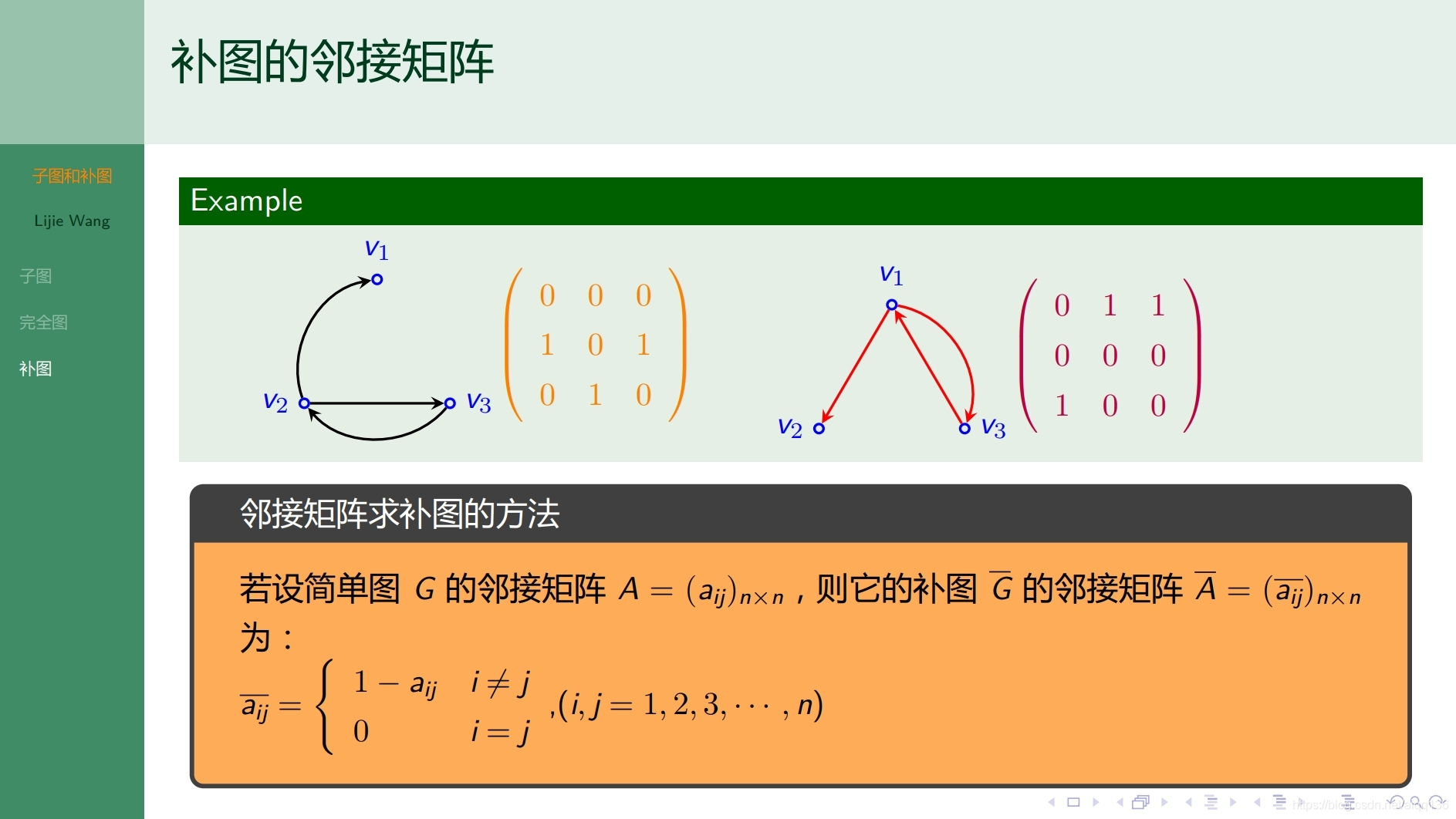
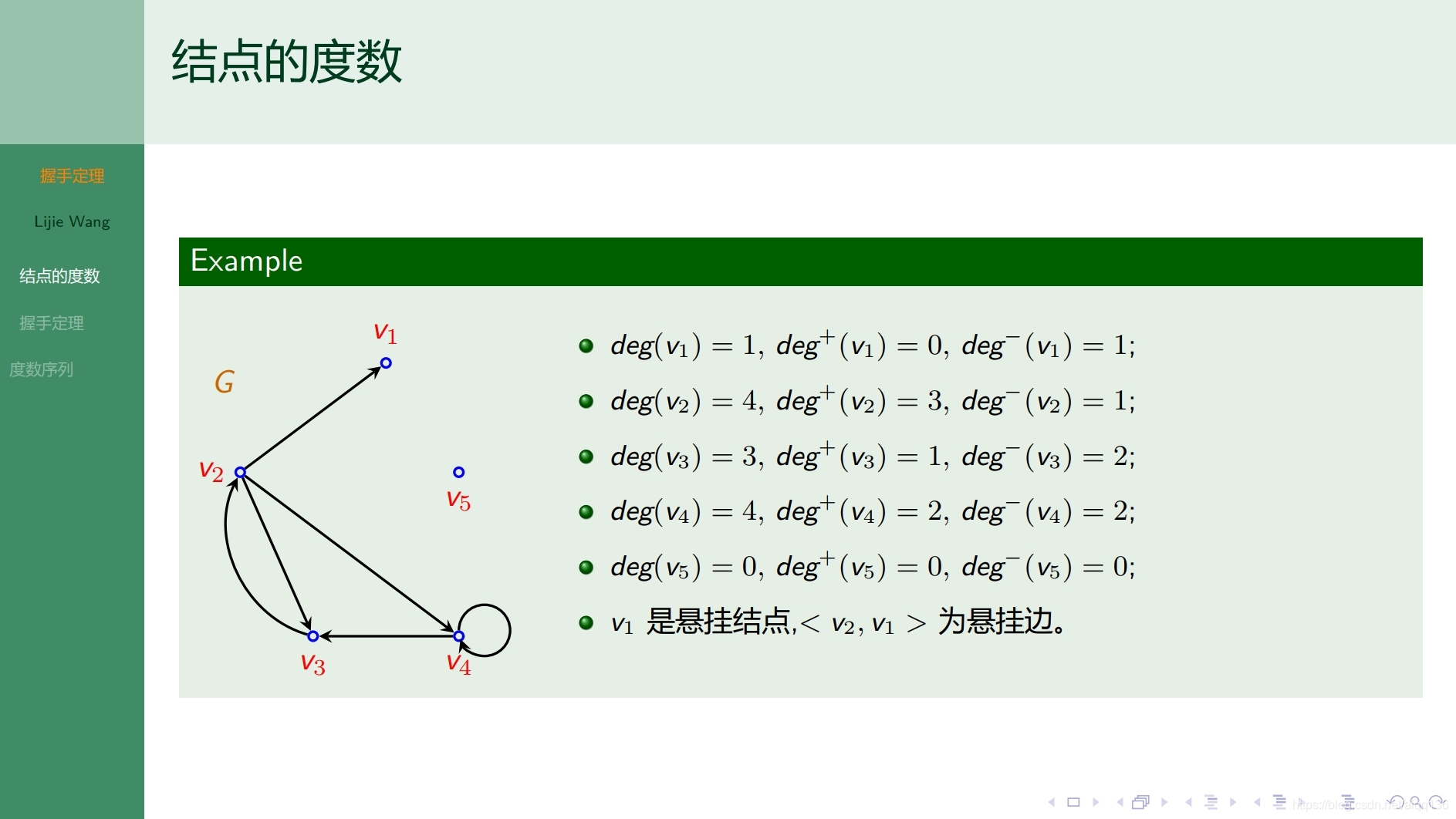
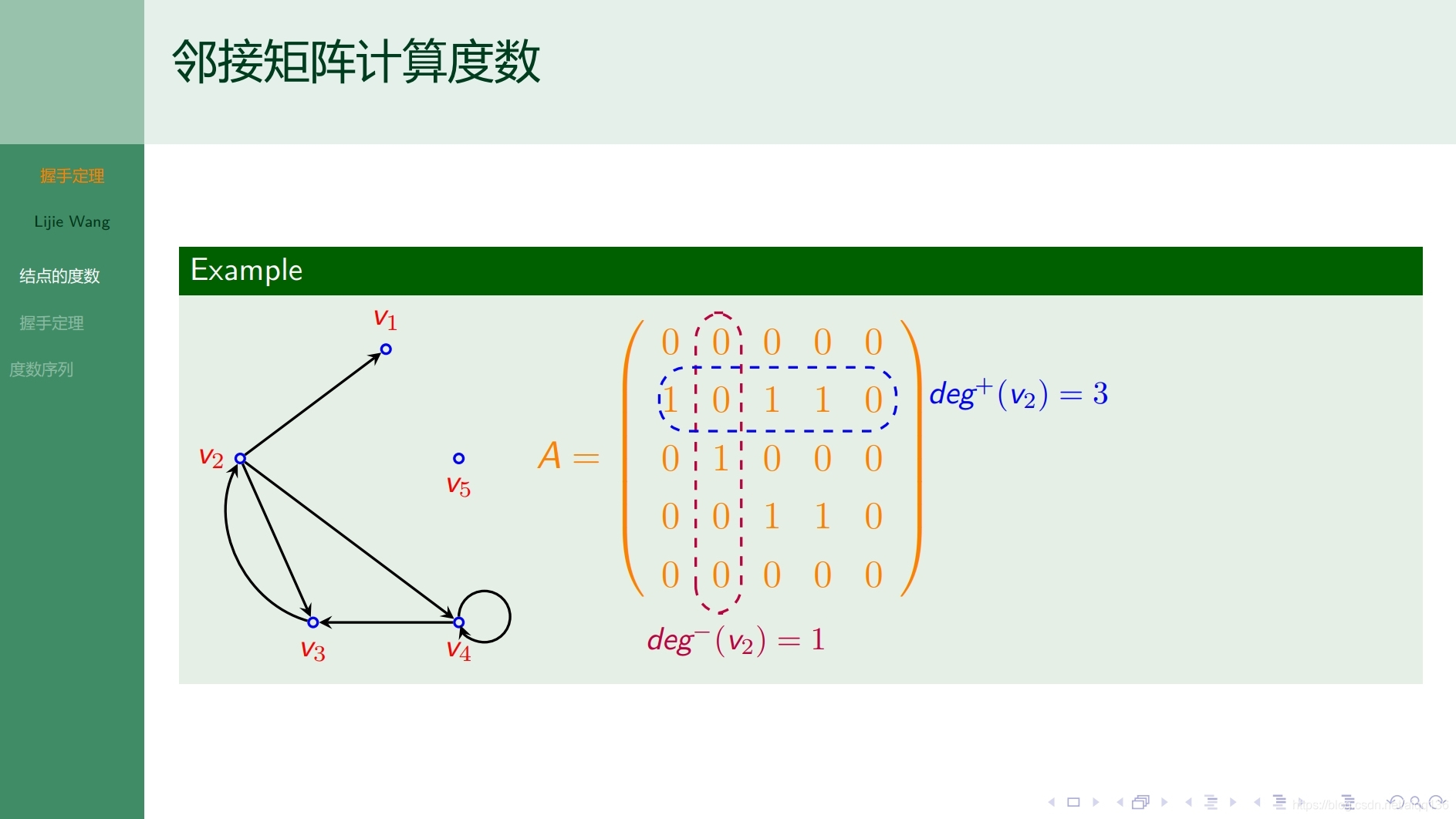
8.1.5图论基础 握手定理

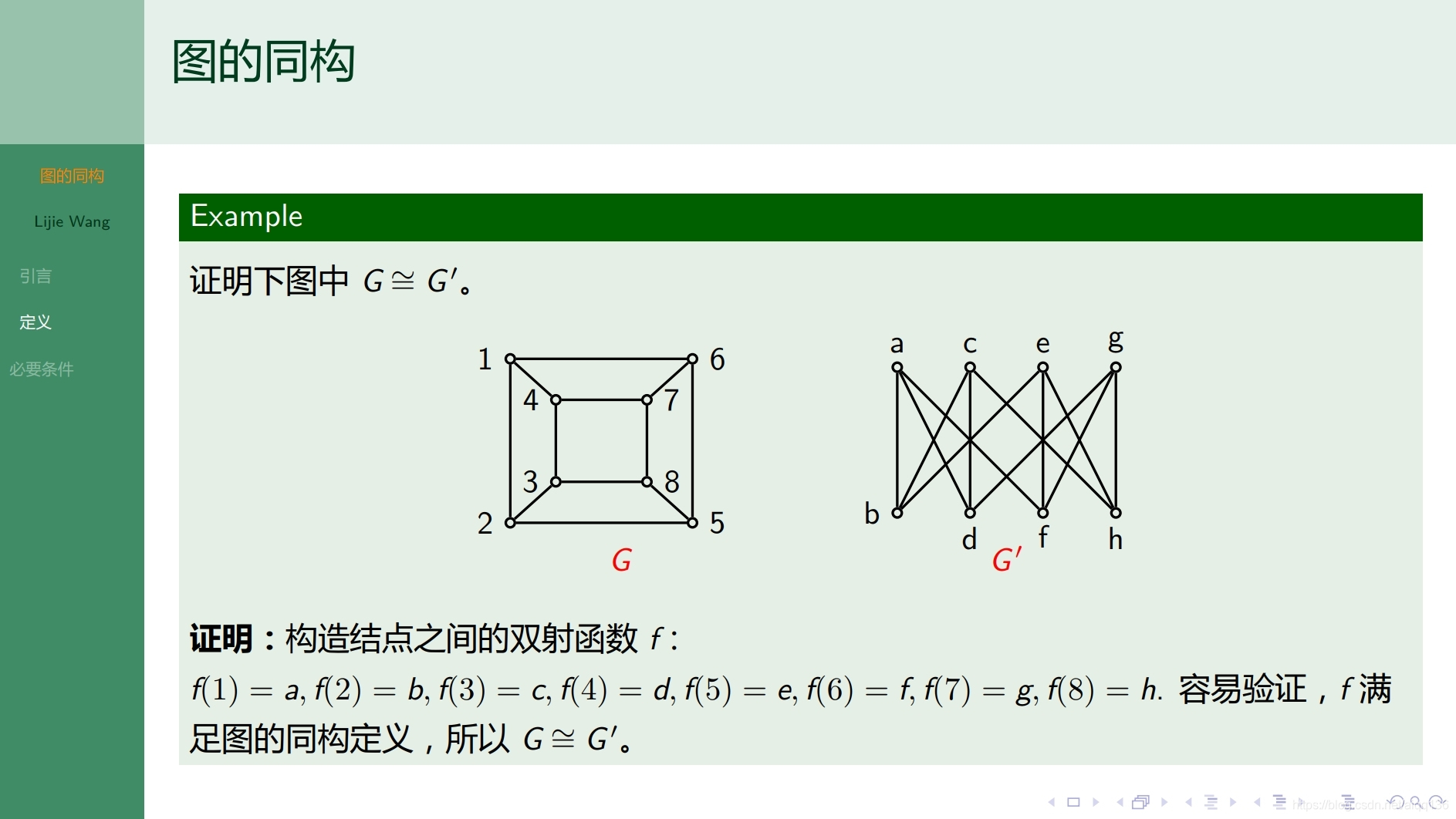
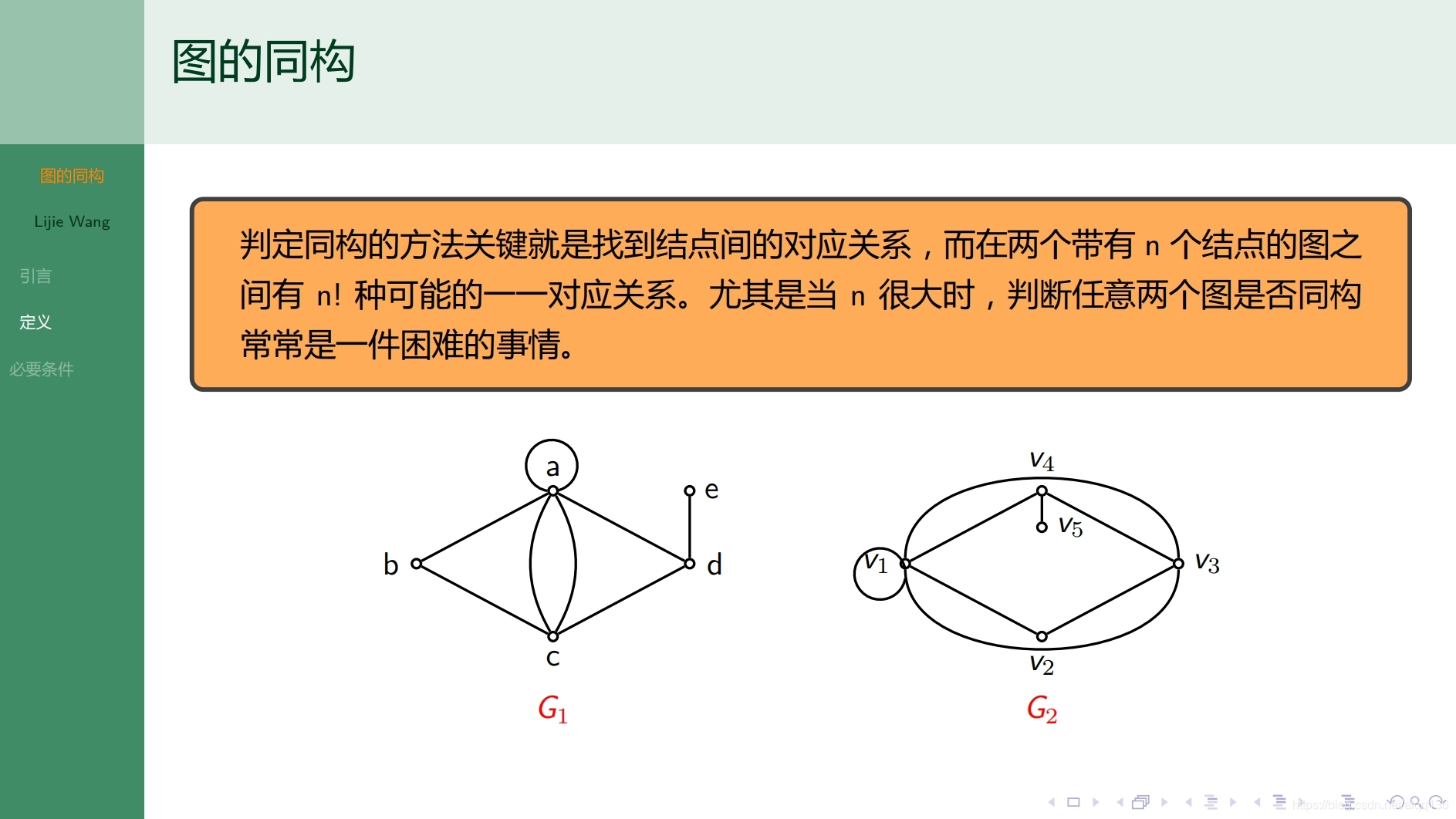
8.1.6图论基础 图的同构

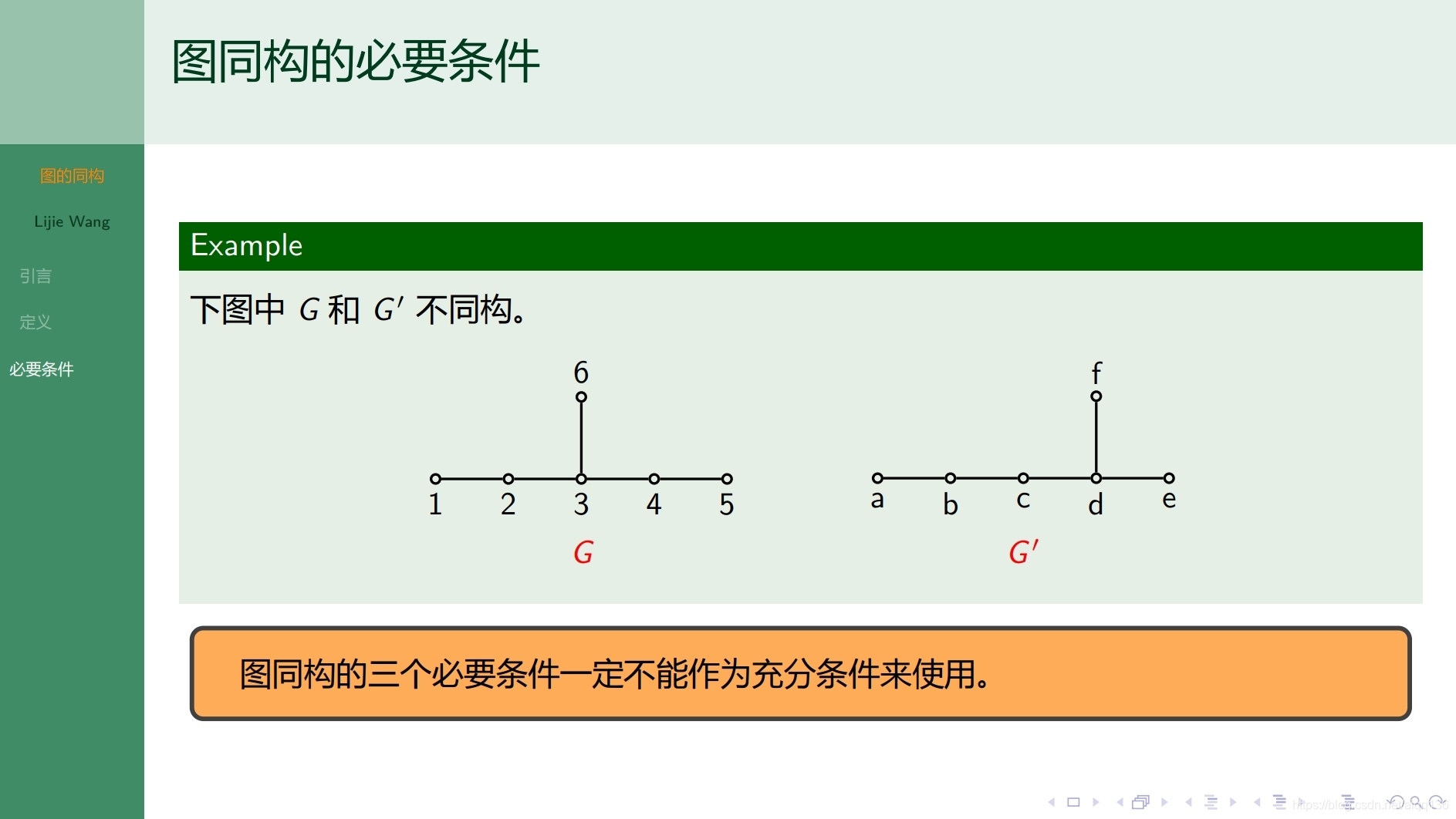
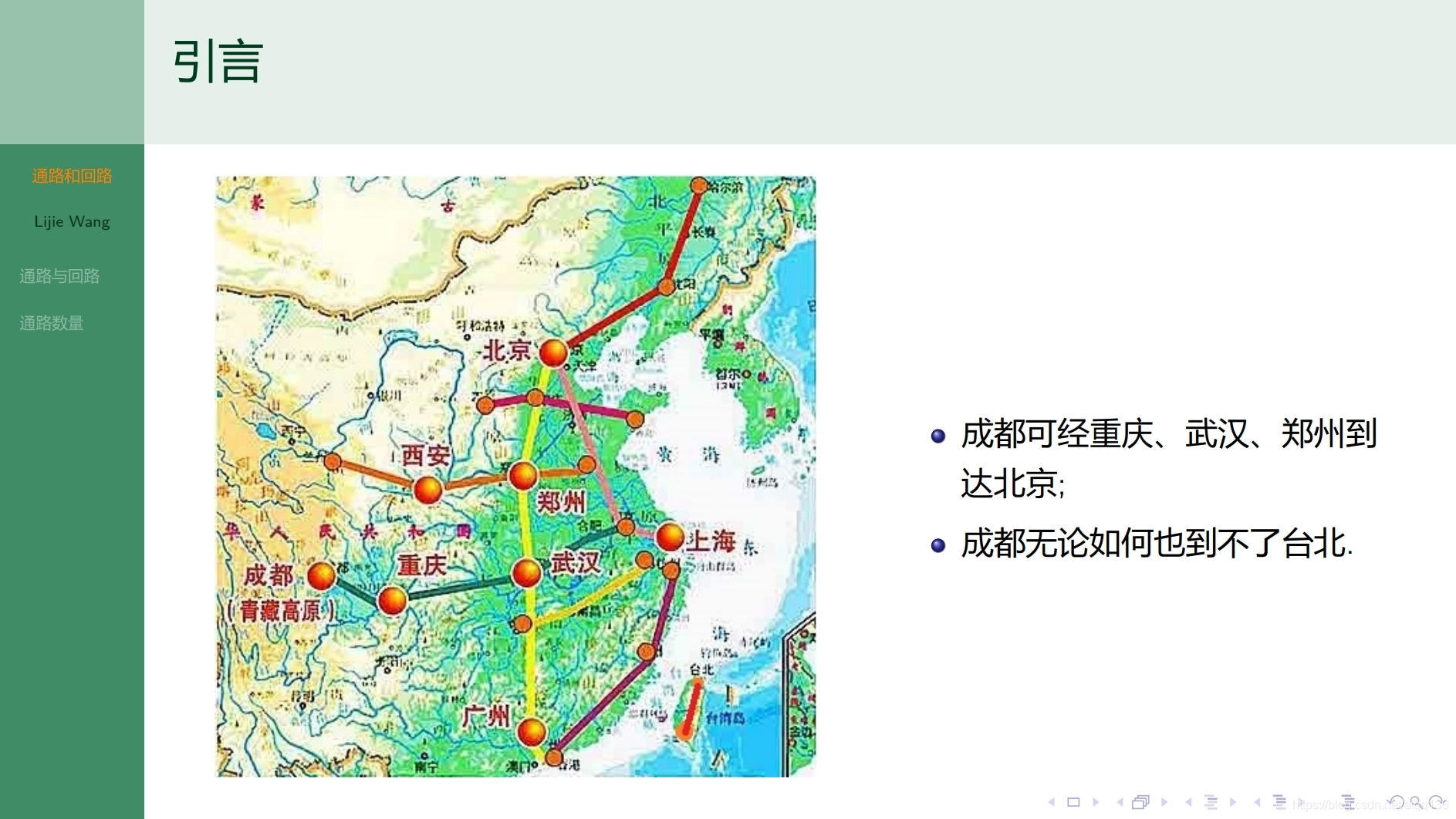
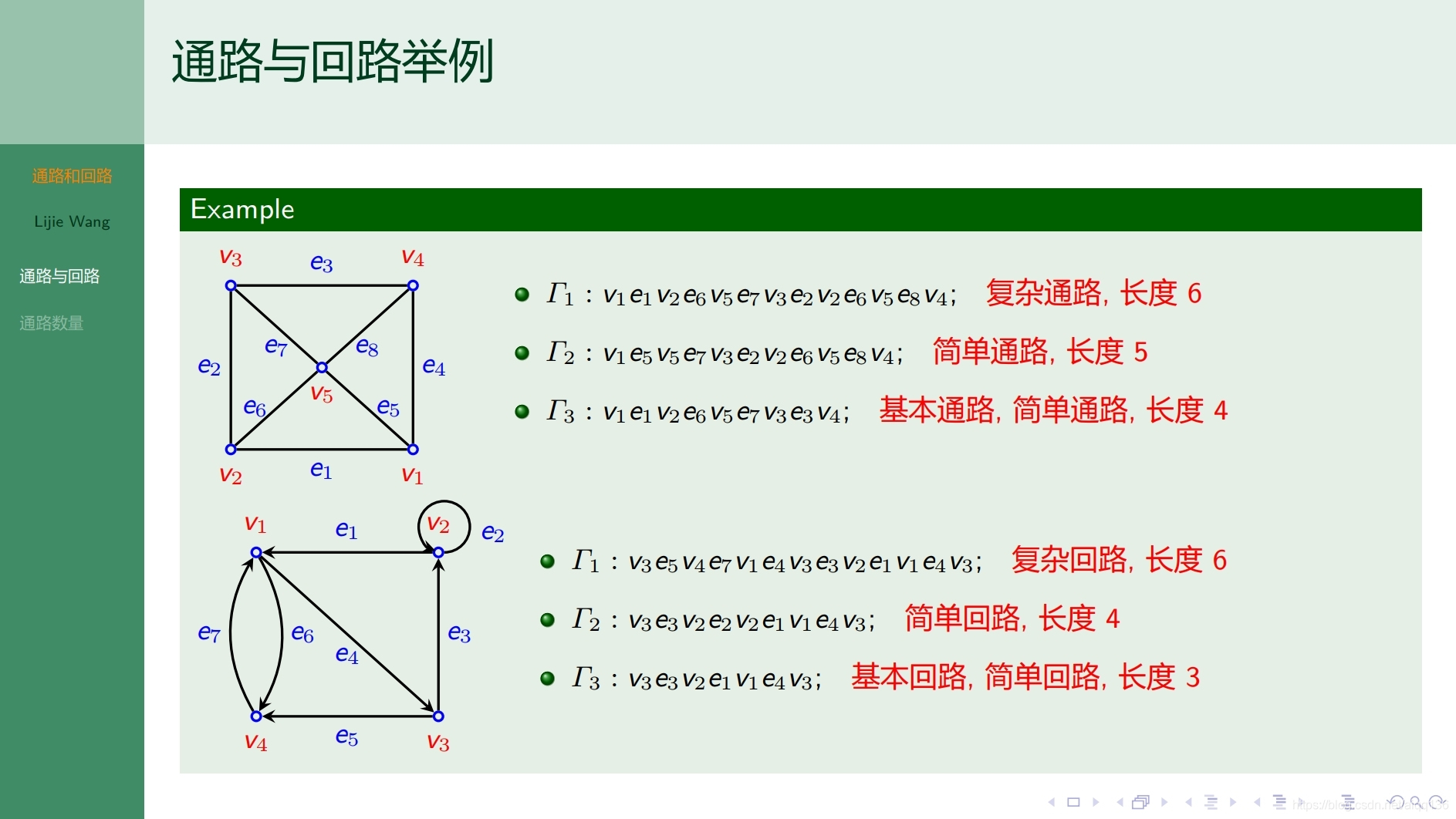
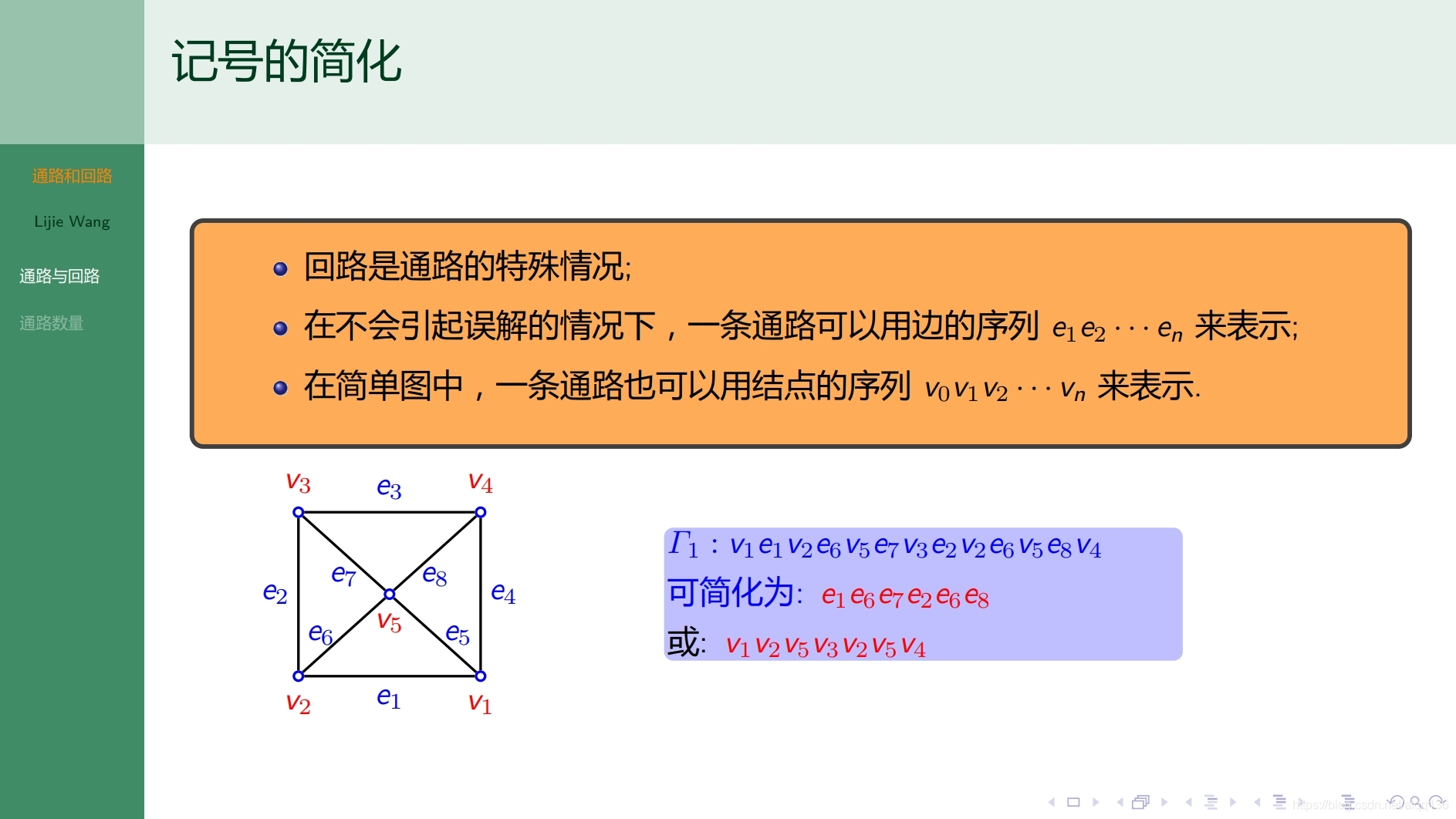
8.2.1图论基础 通路和回路

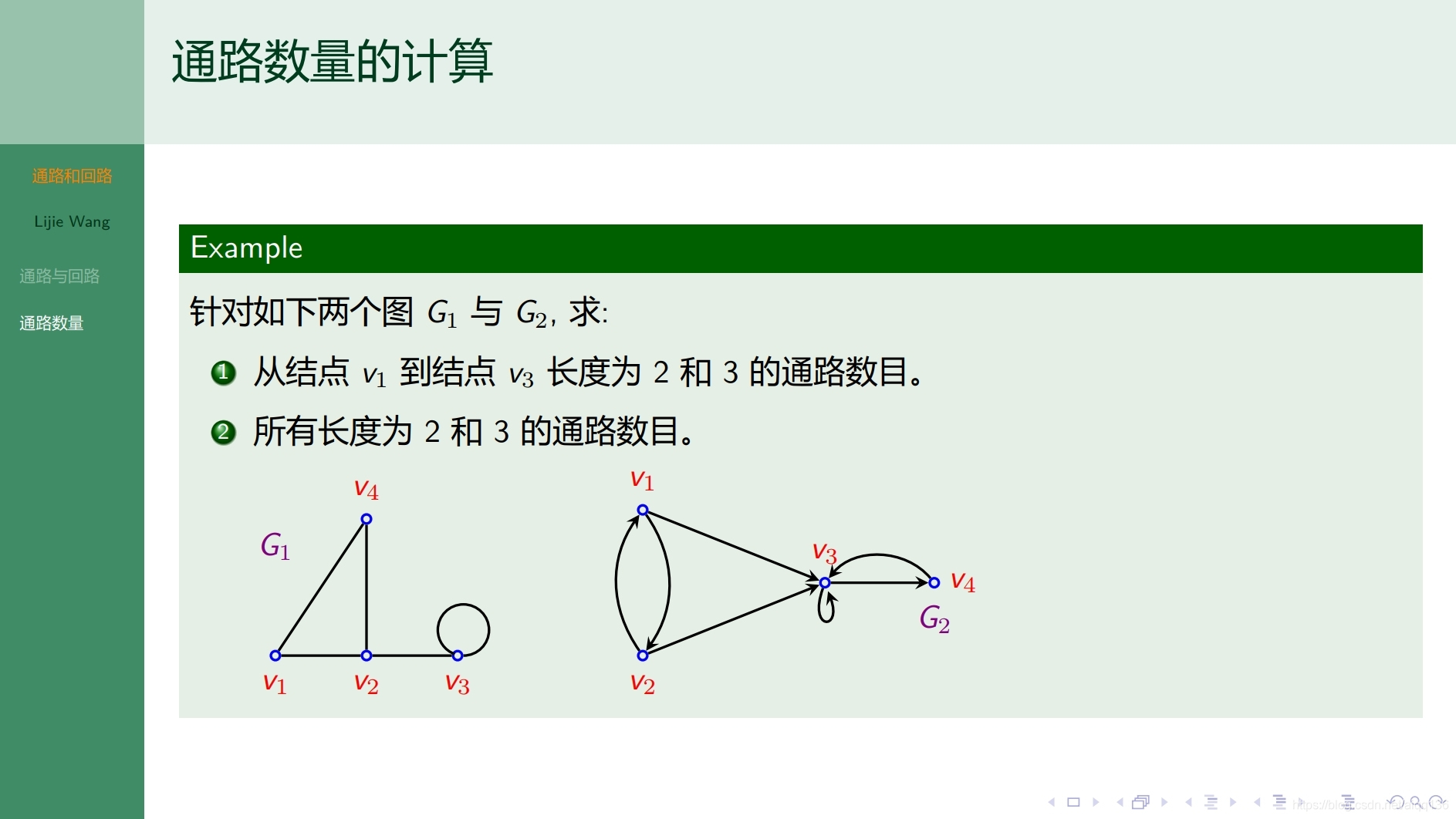
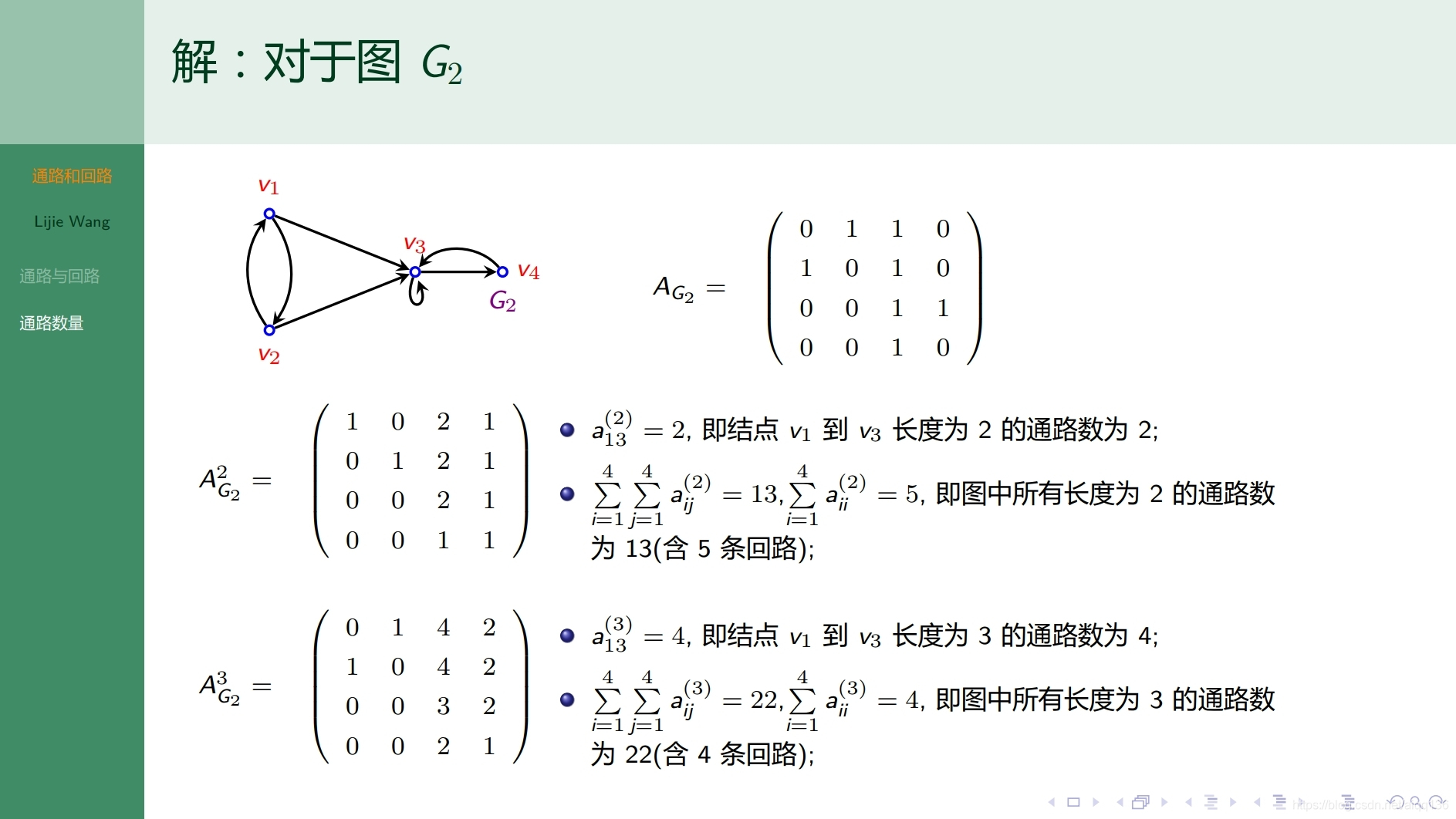
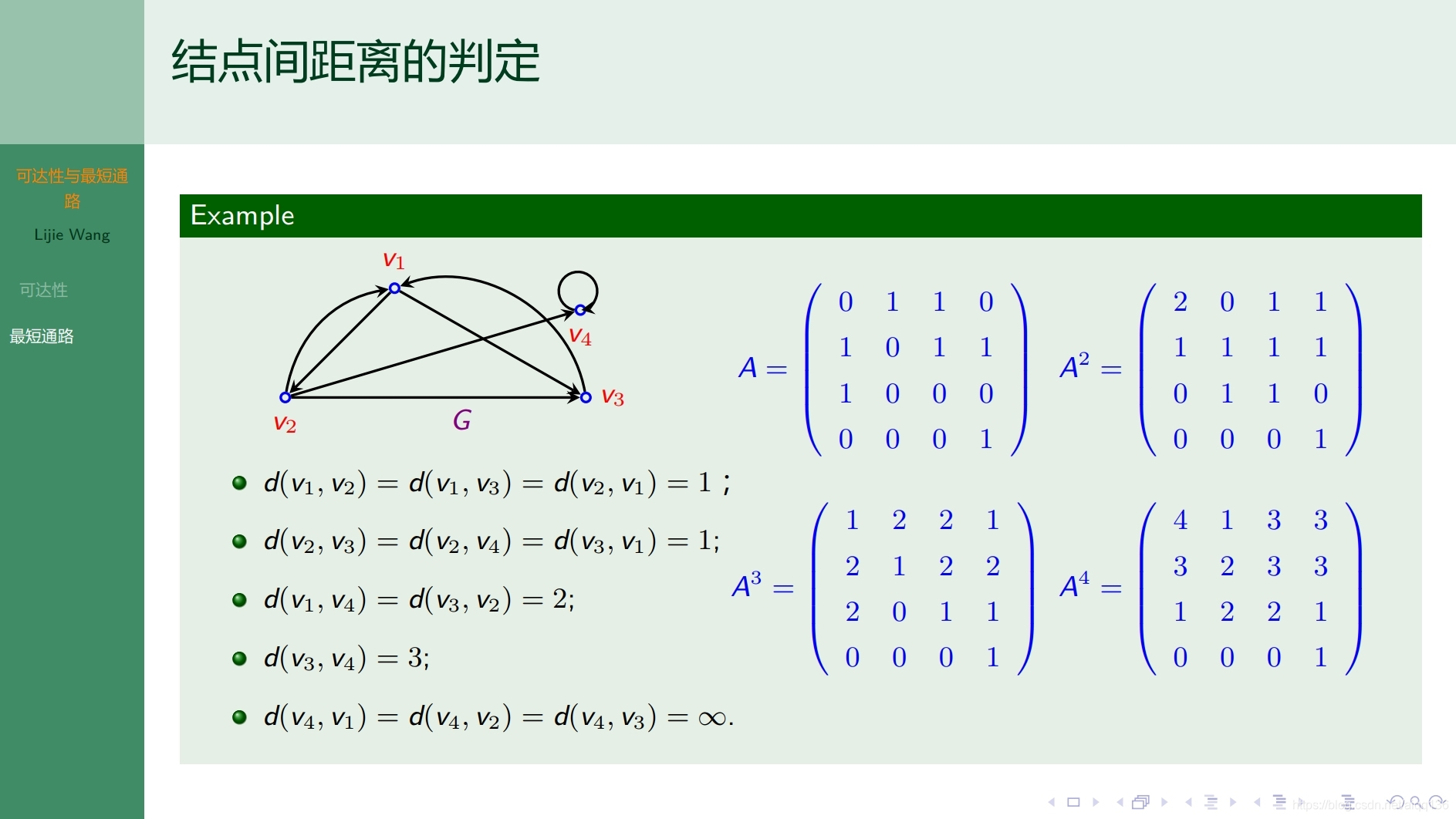
8.2.2图论基础 可达性与最短通路

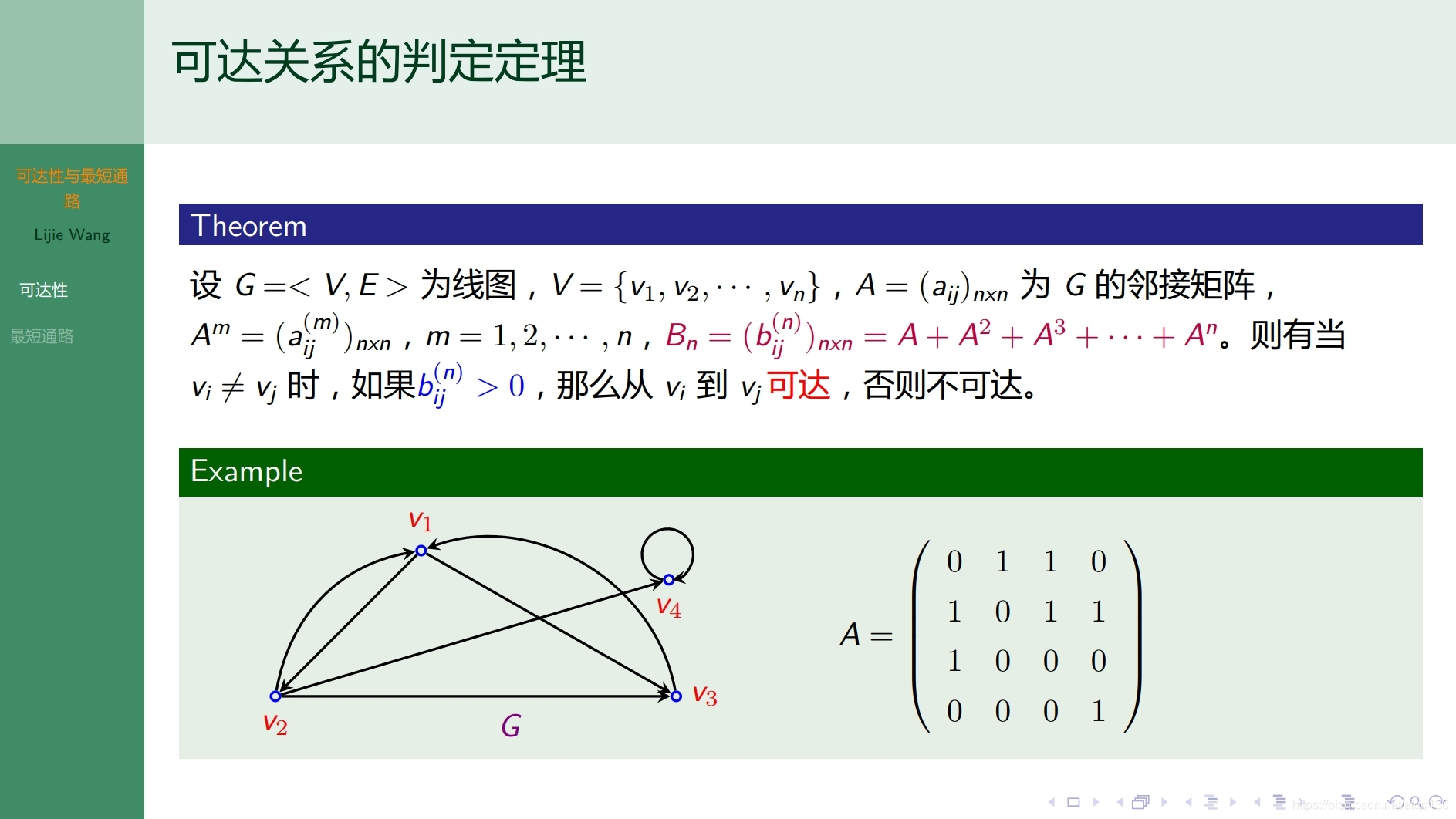
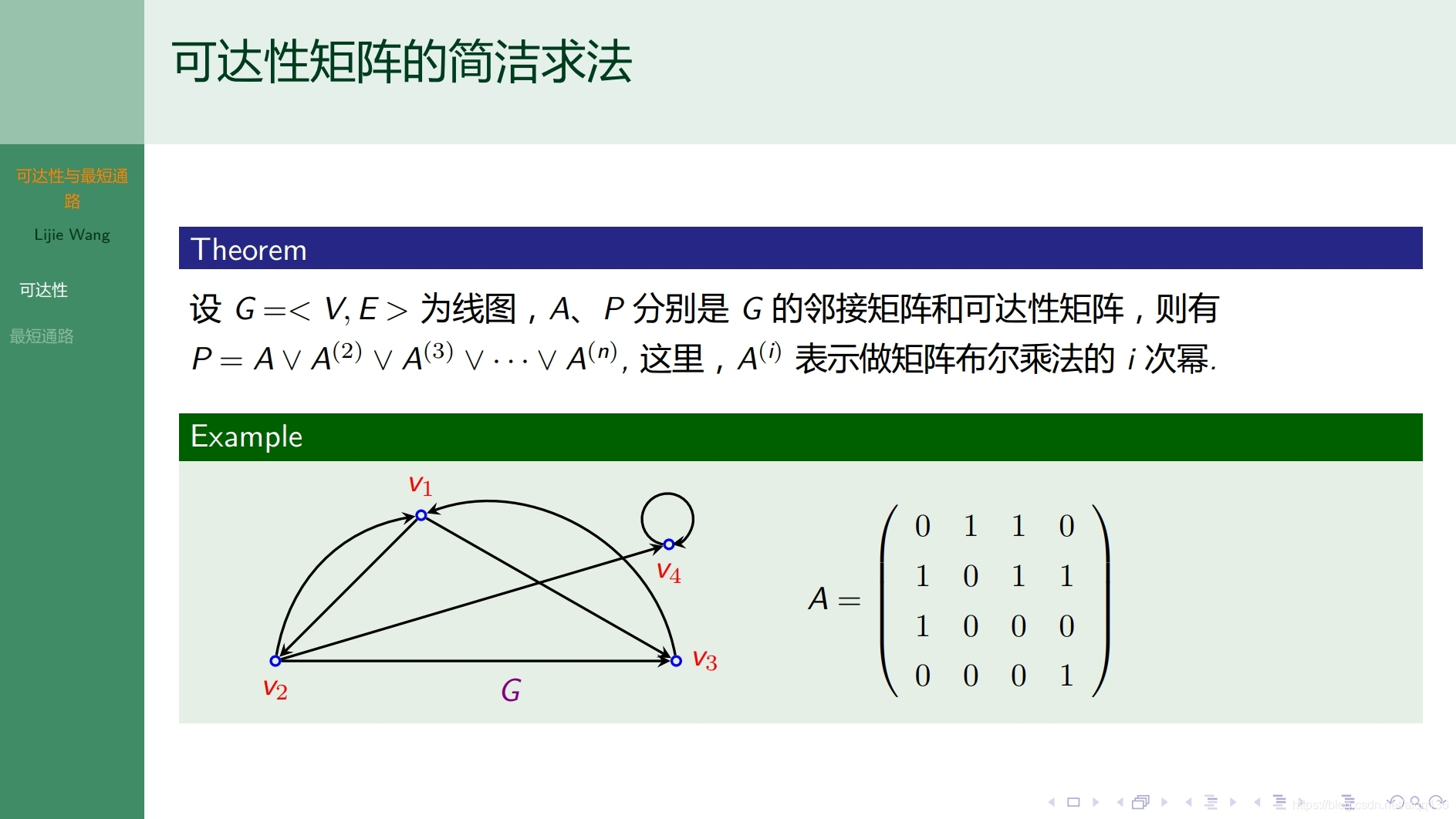
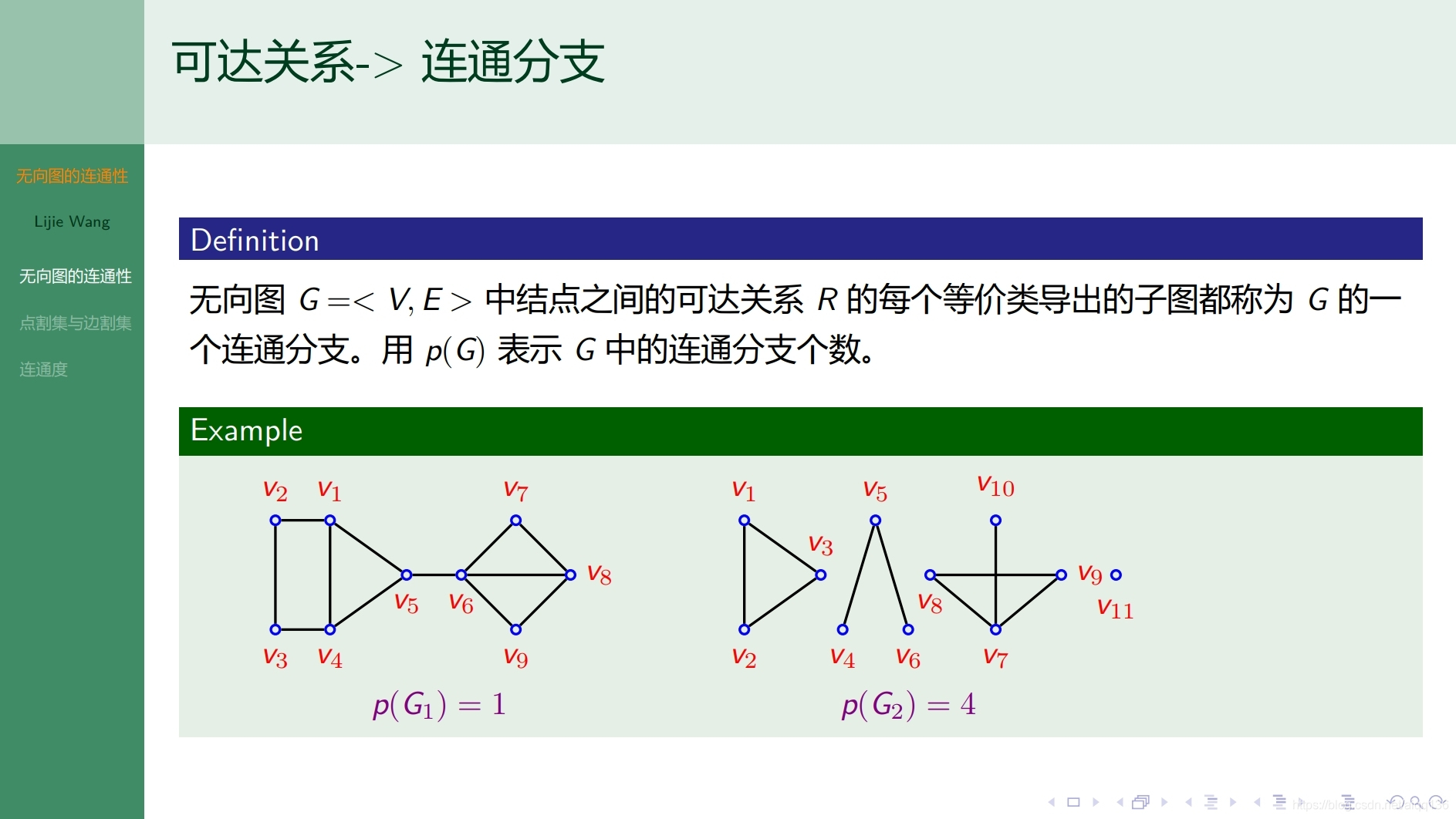
8.2.3图论基础 无向图的连通性

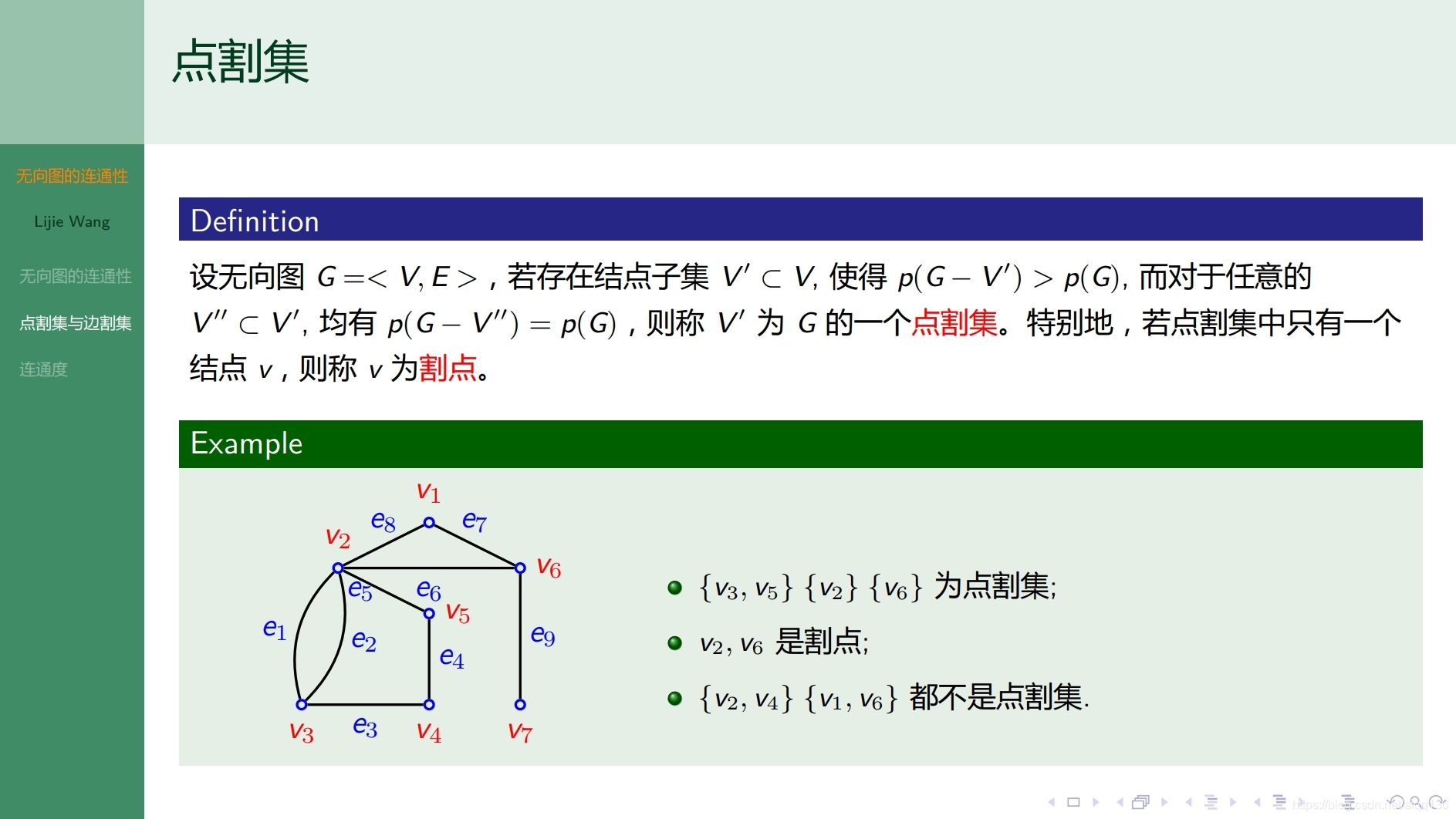
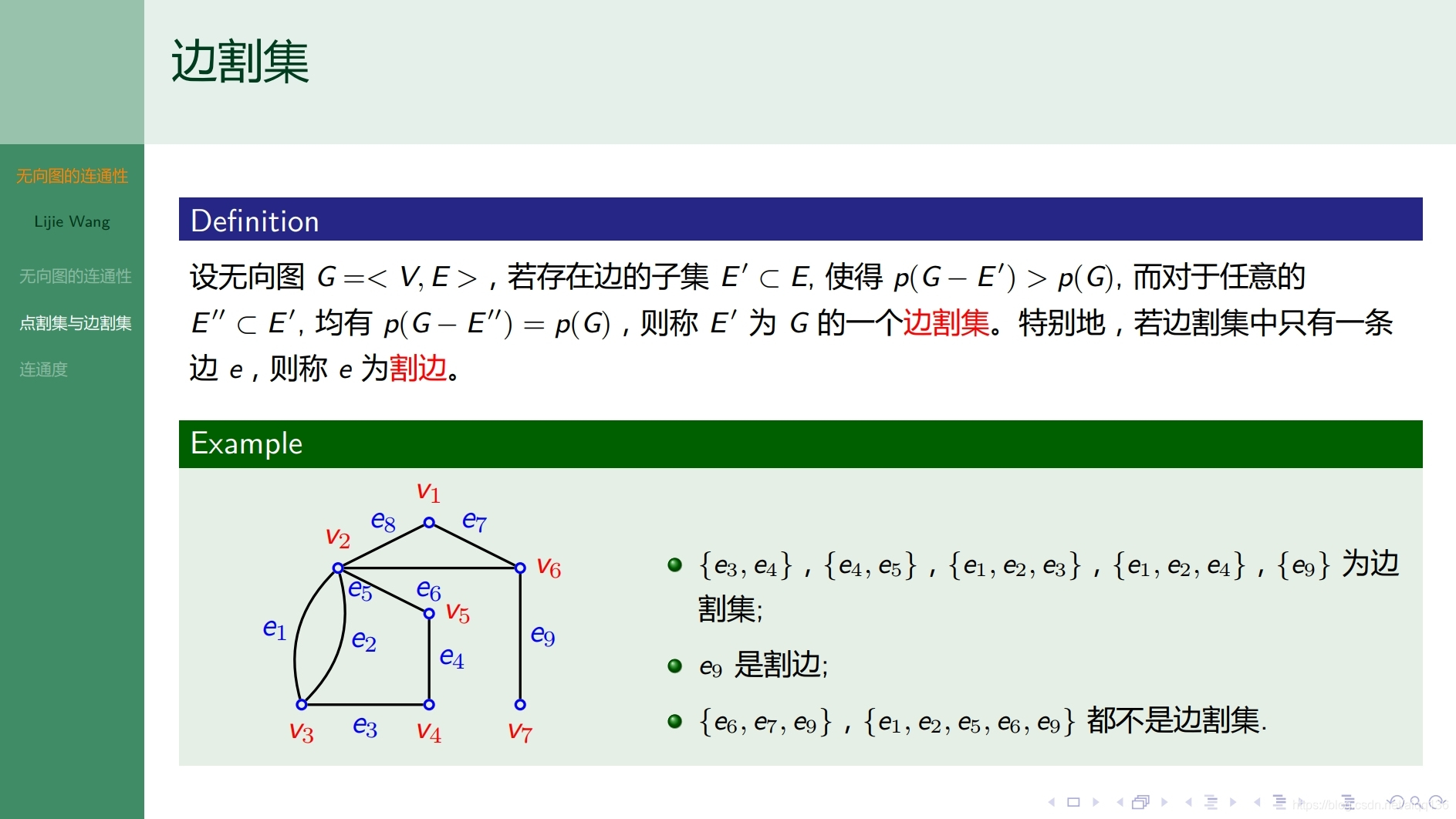
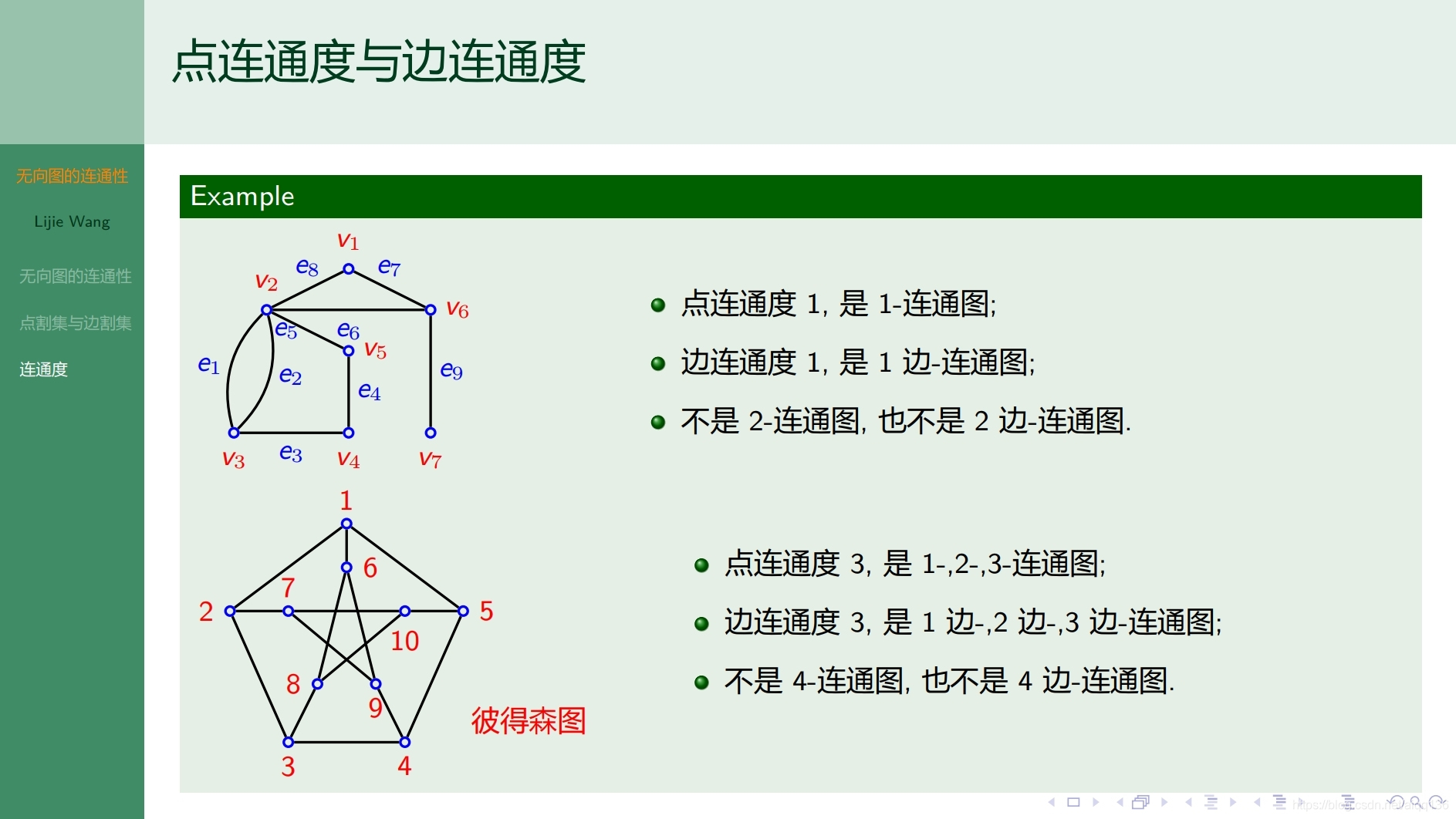
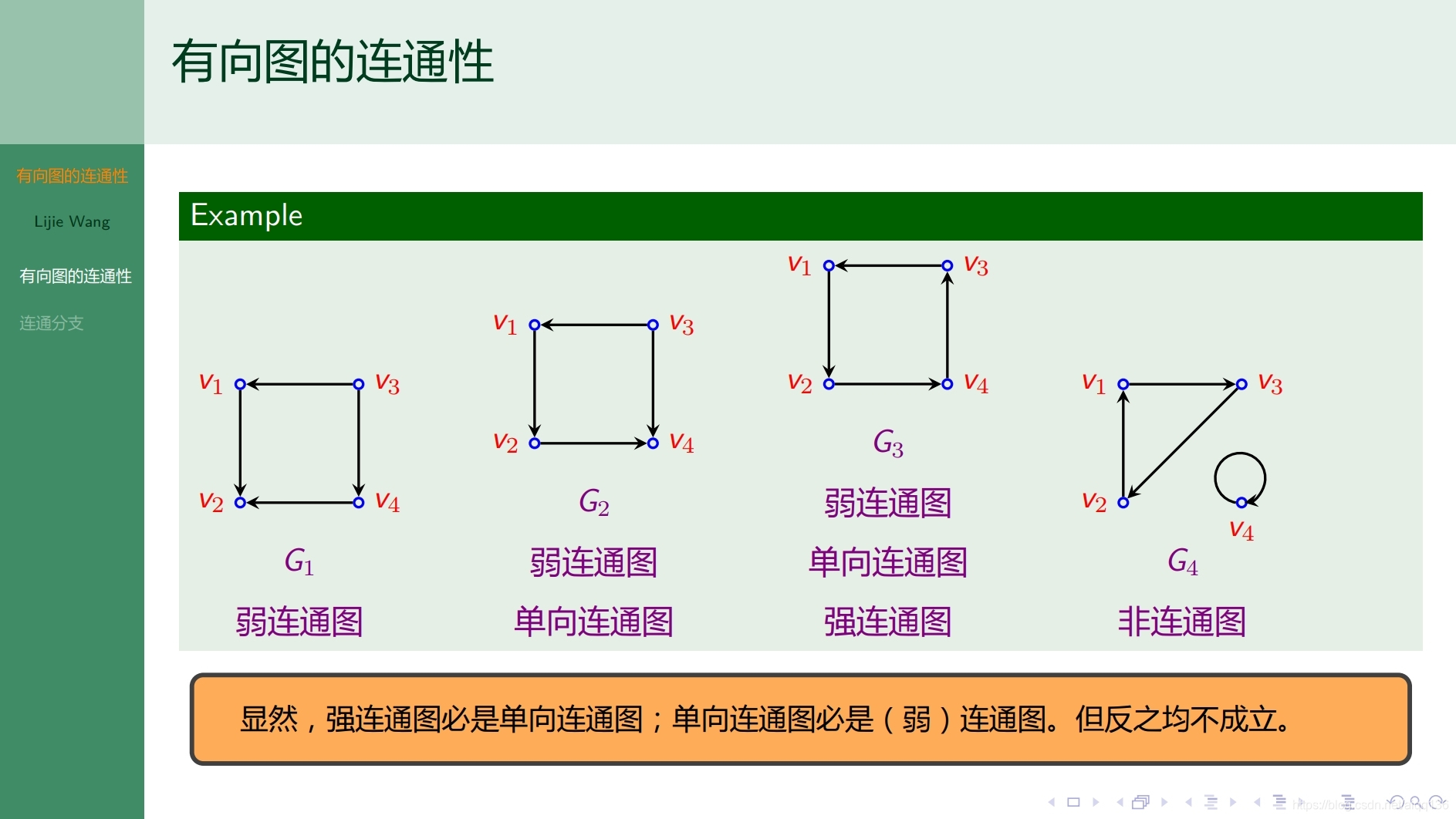
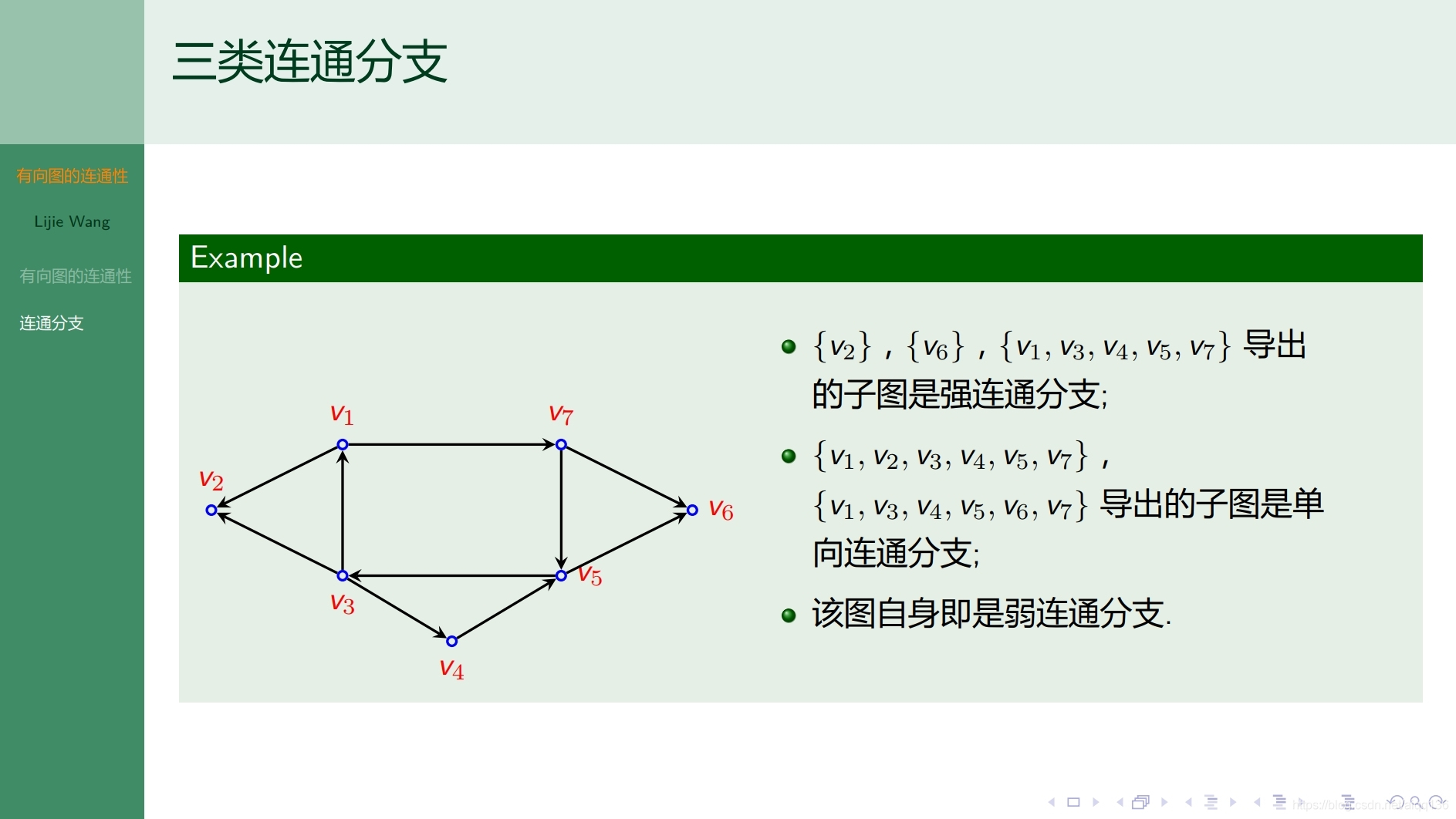
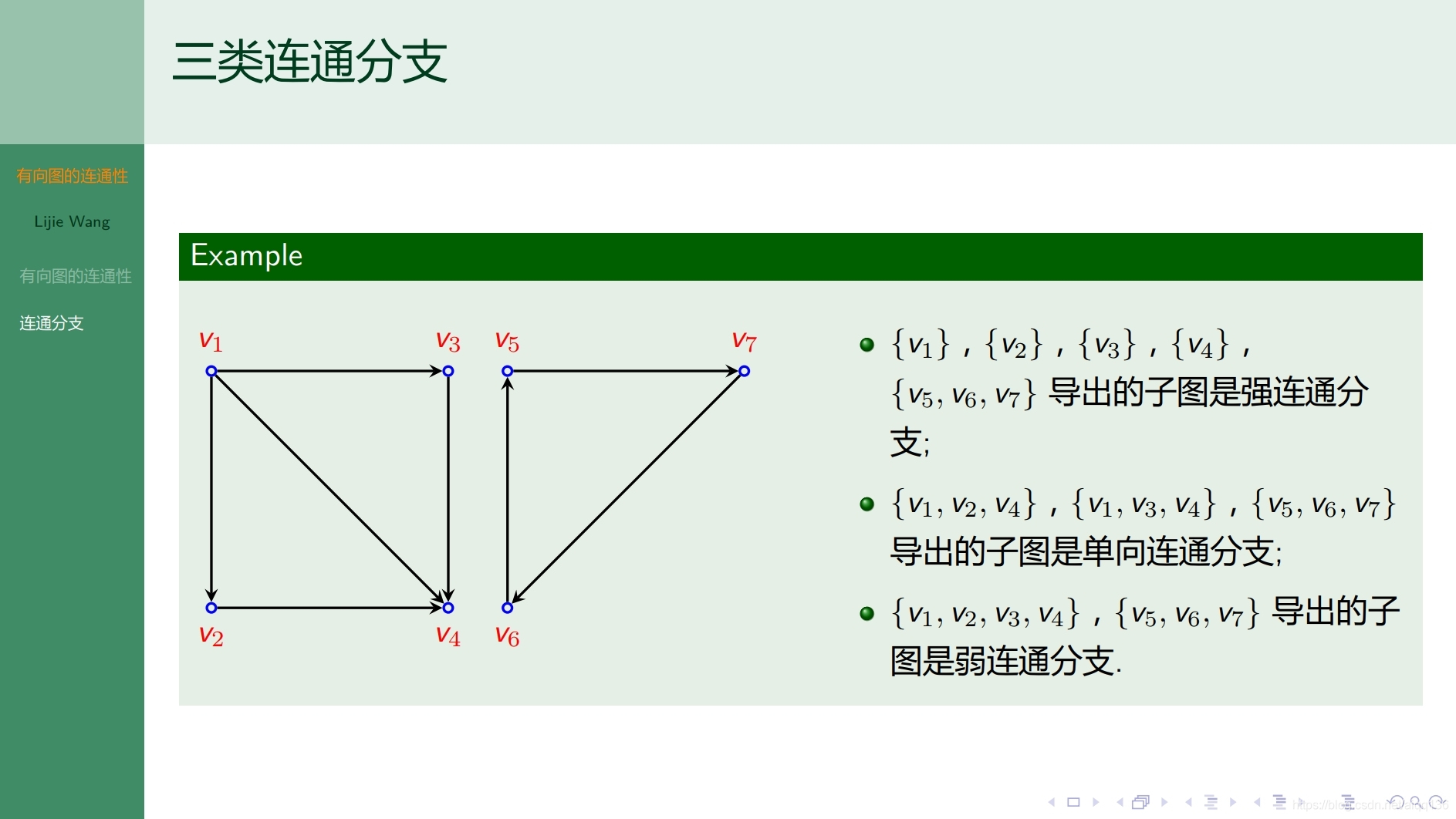
8.2.4图论基础 有向图的连通性

9.1.1树 认识树

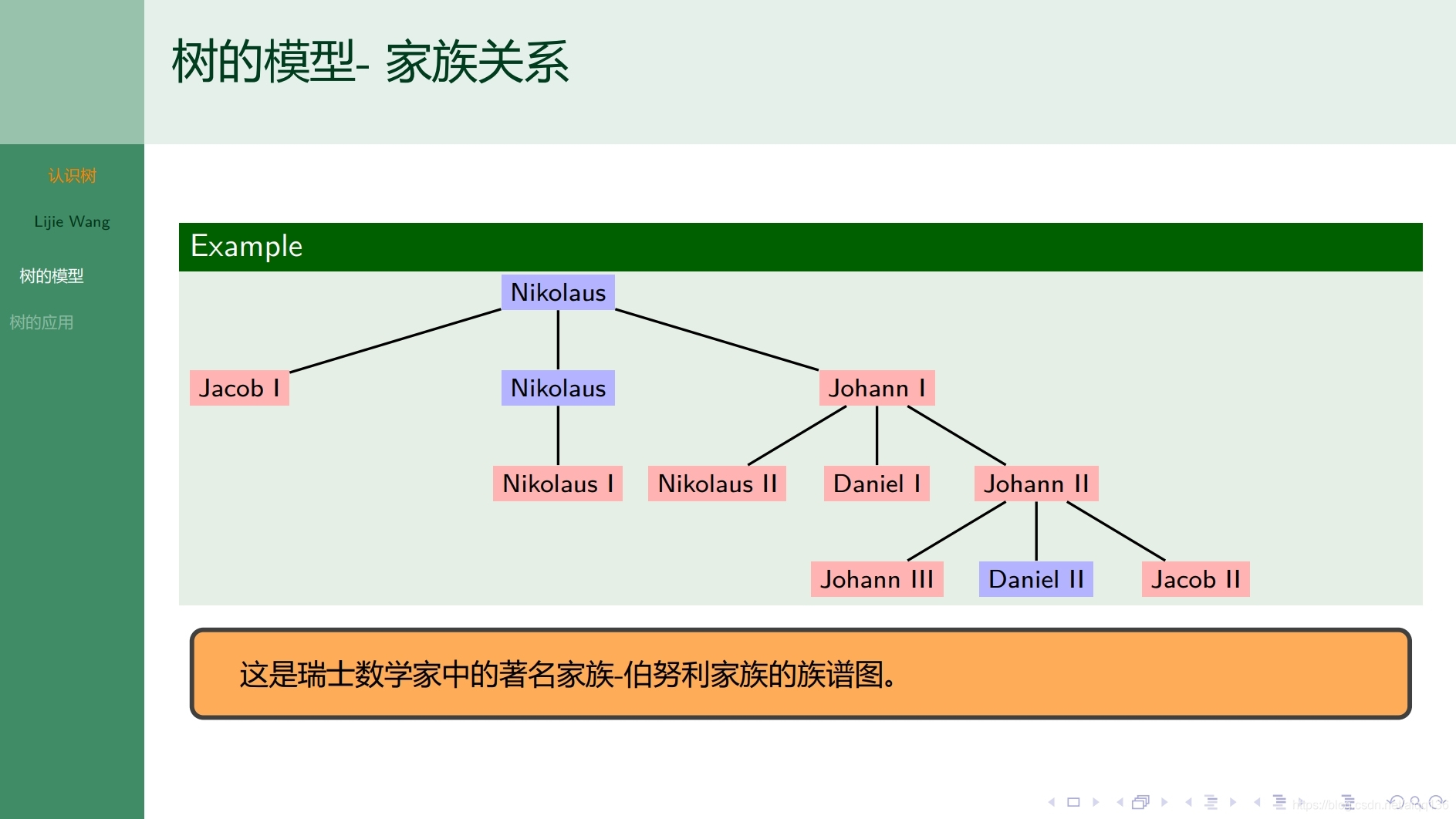
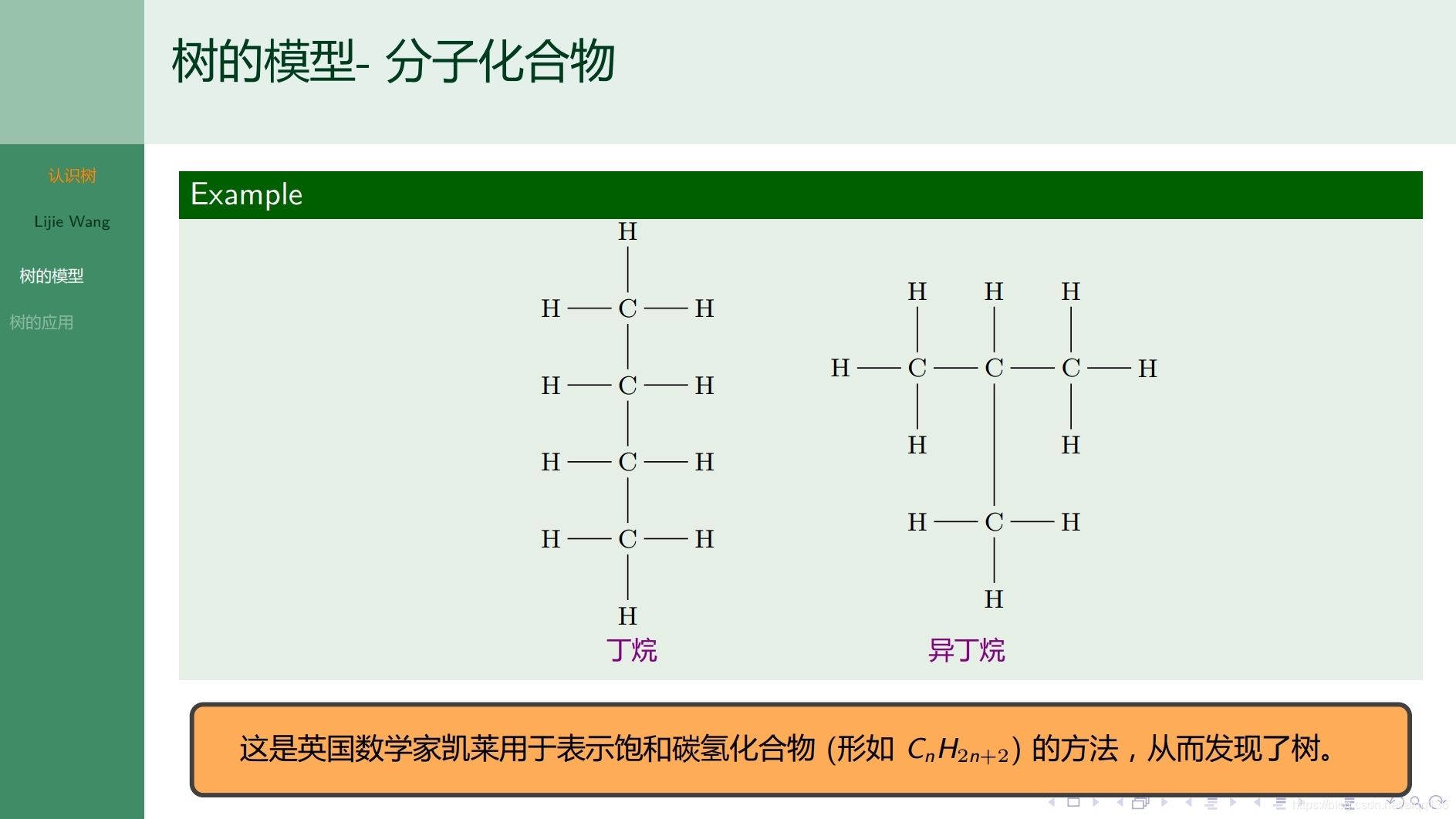
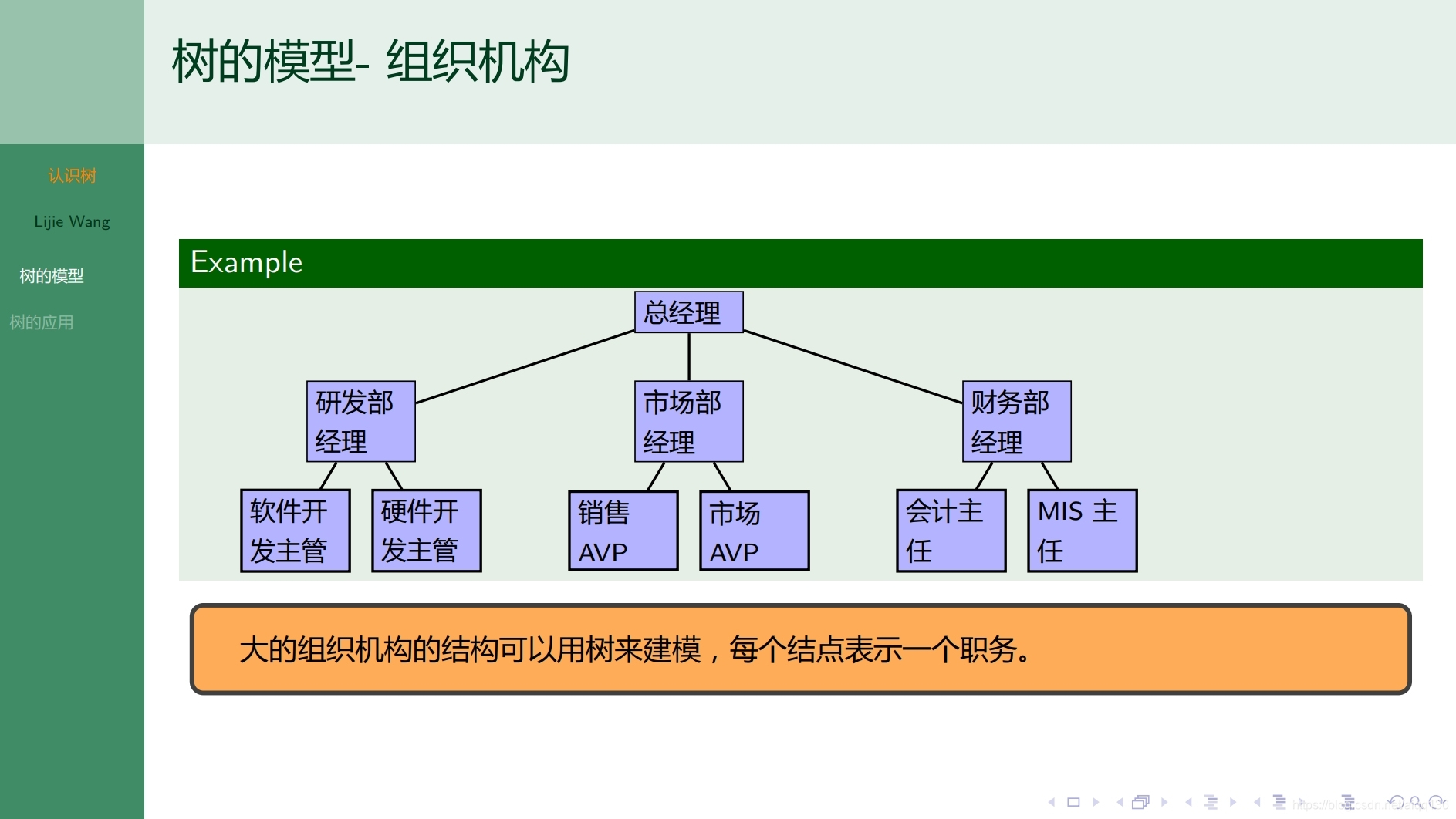
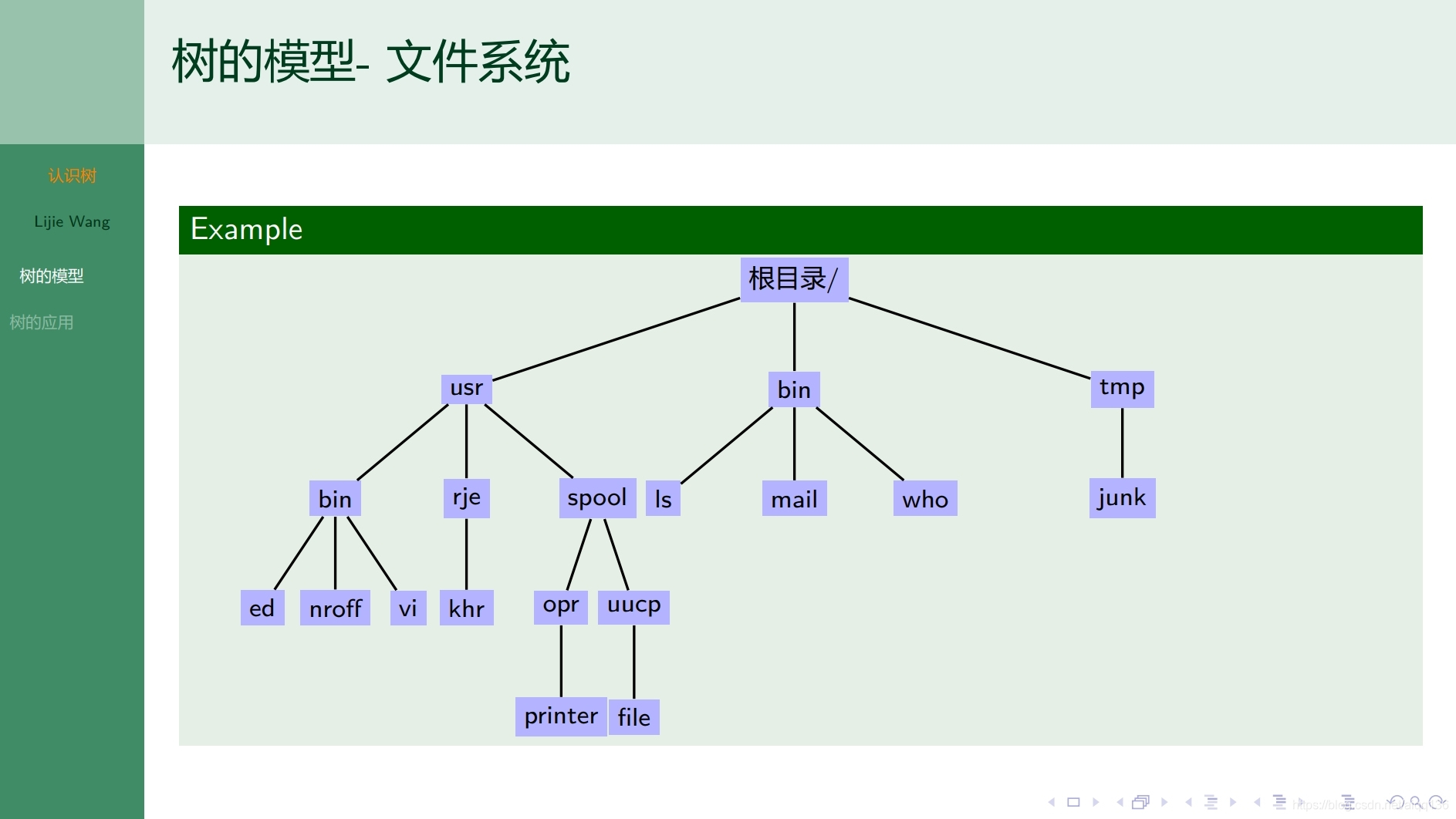
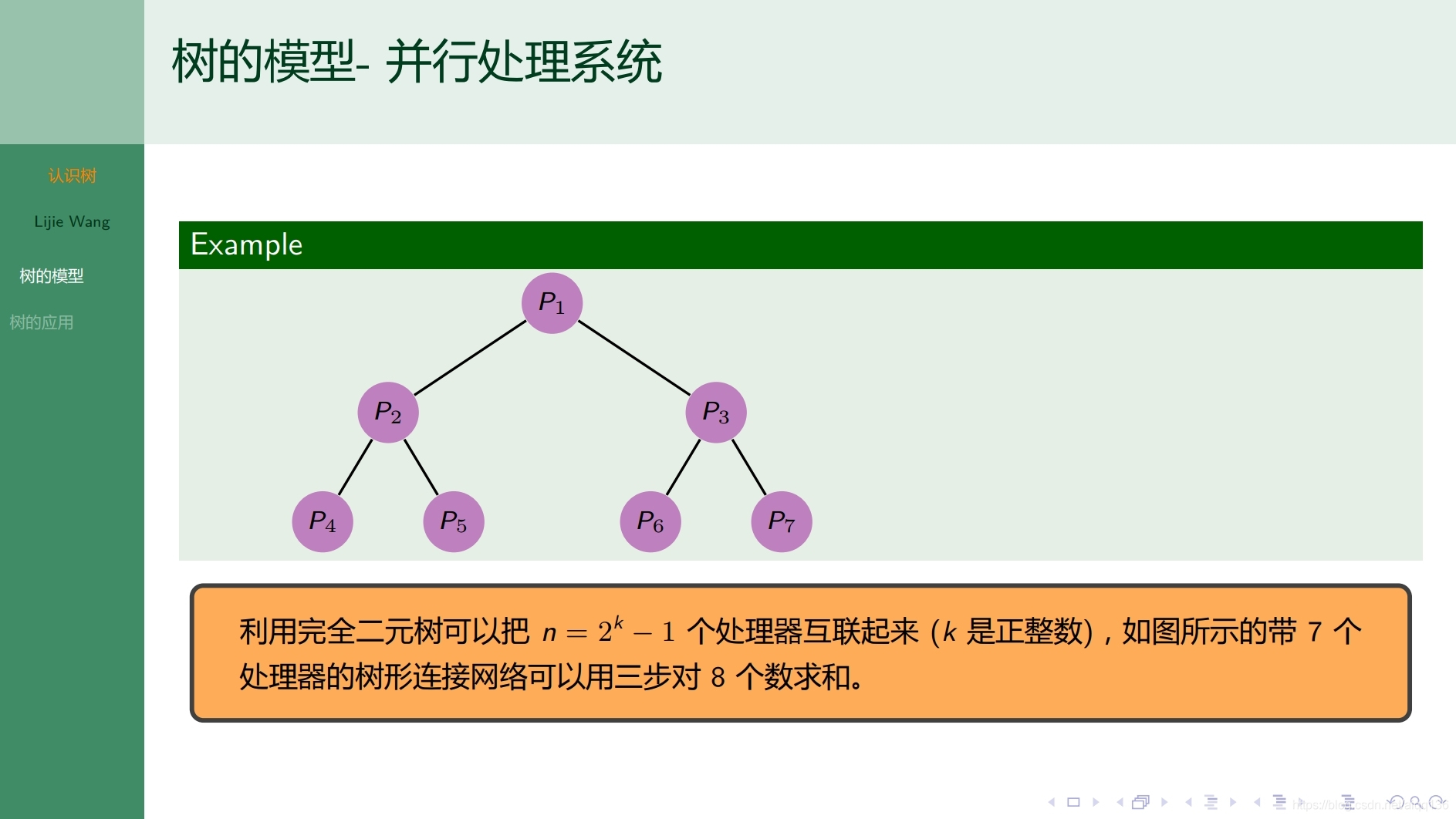
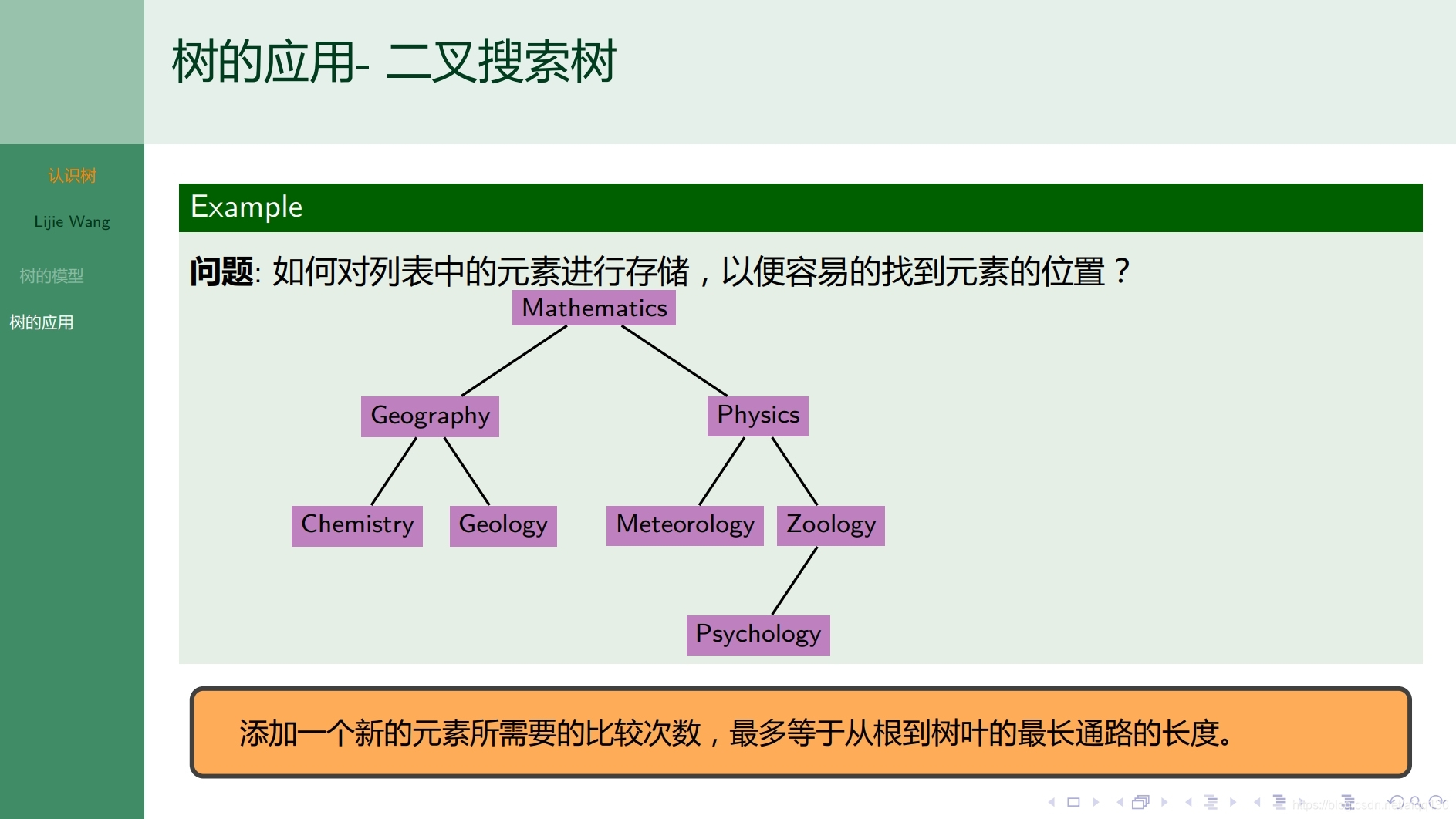
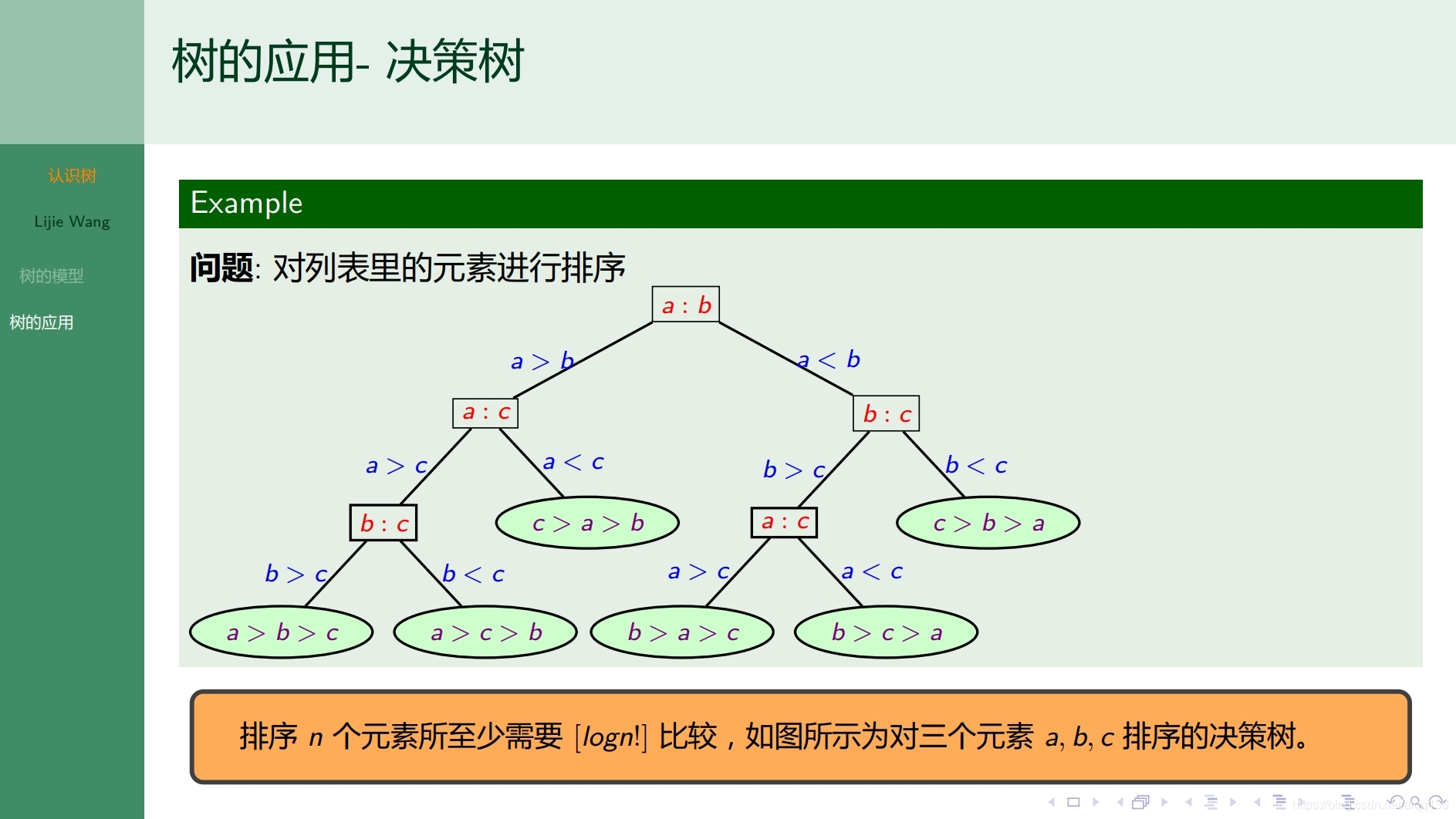
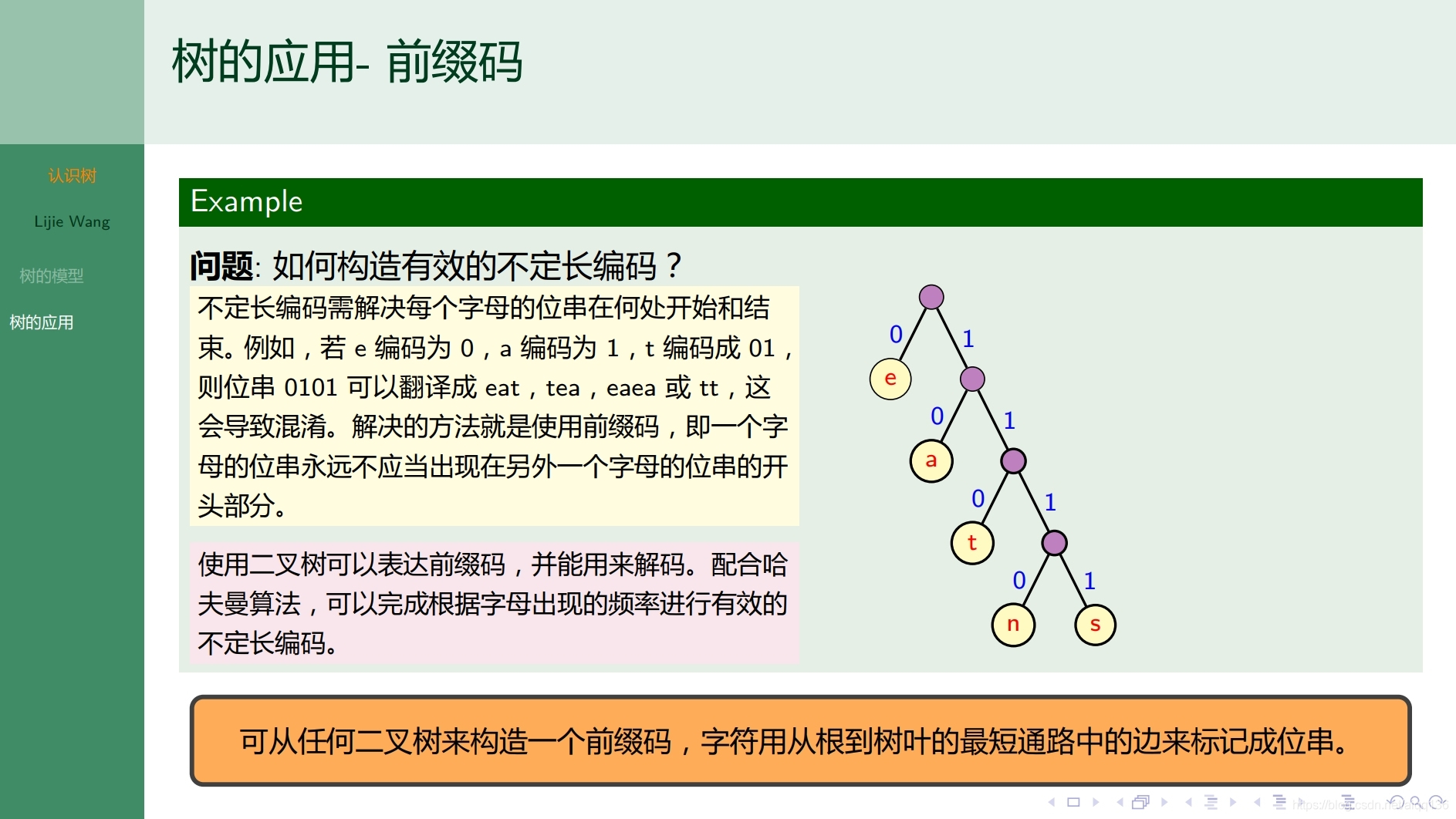
9.1.2树 无向树

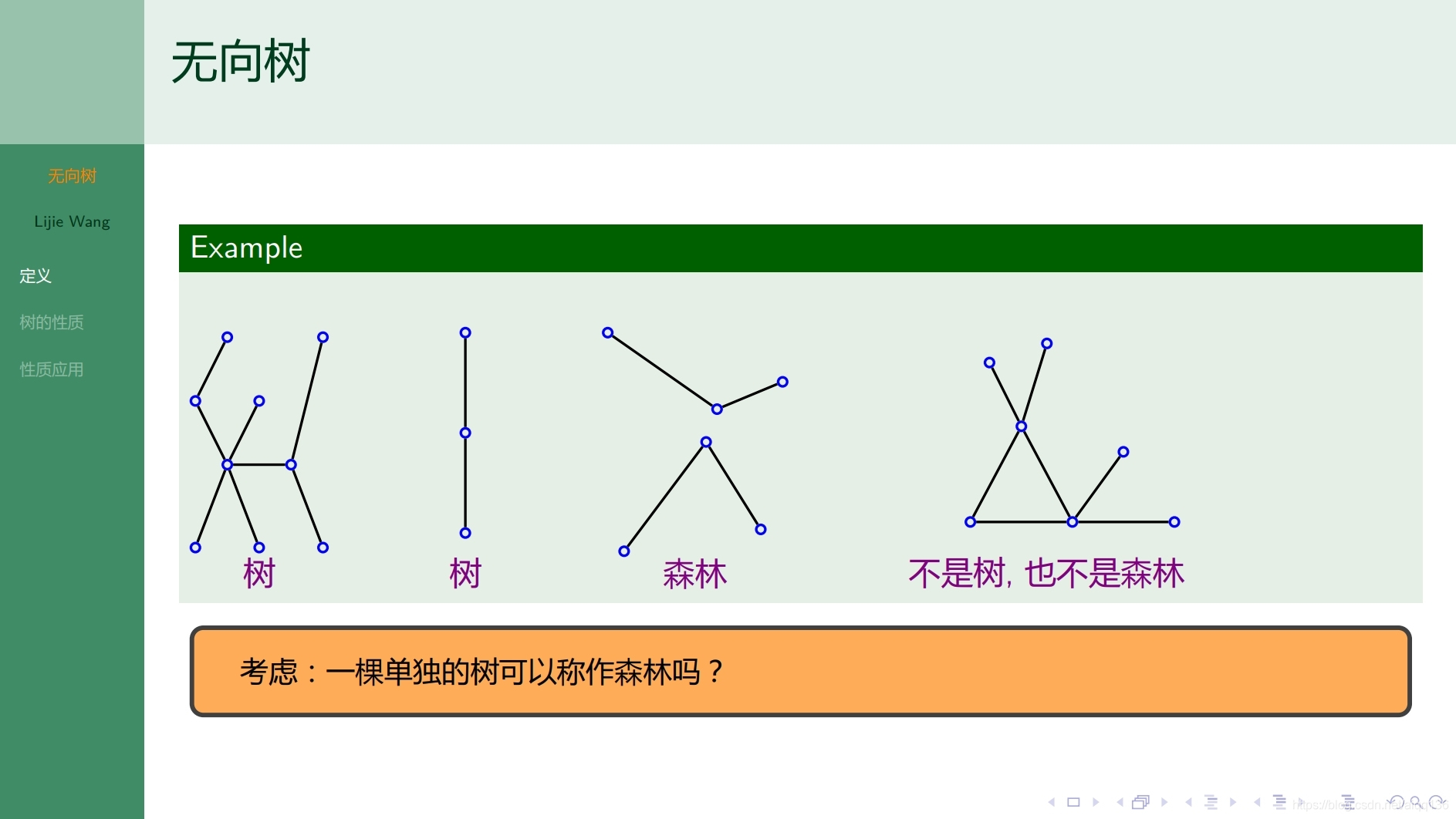
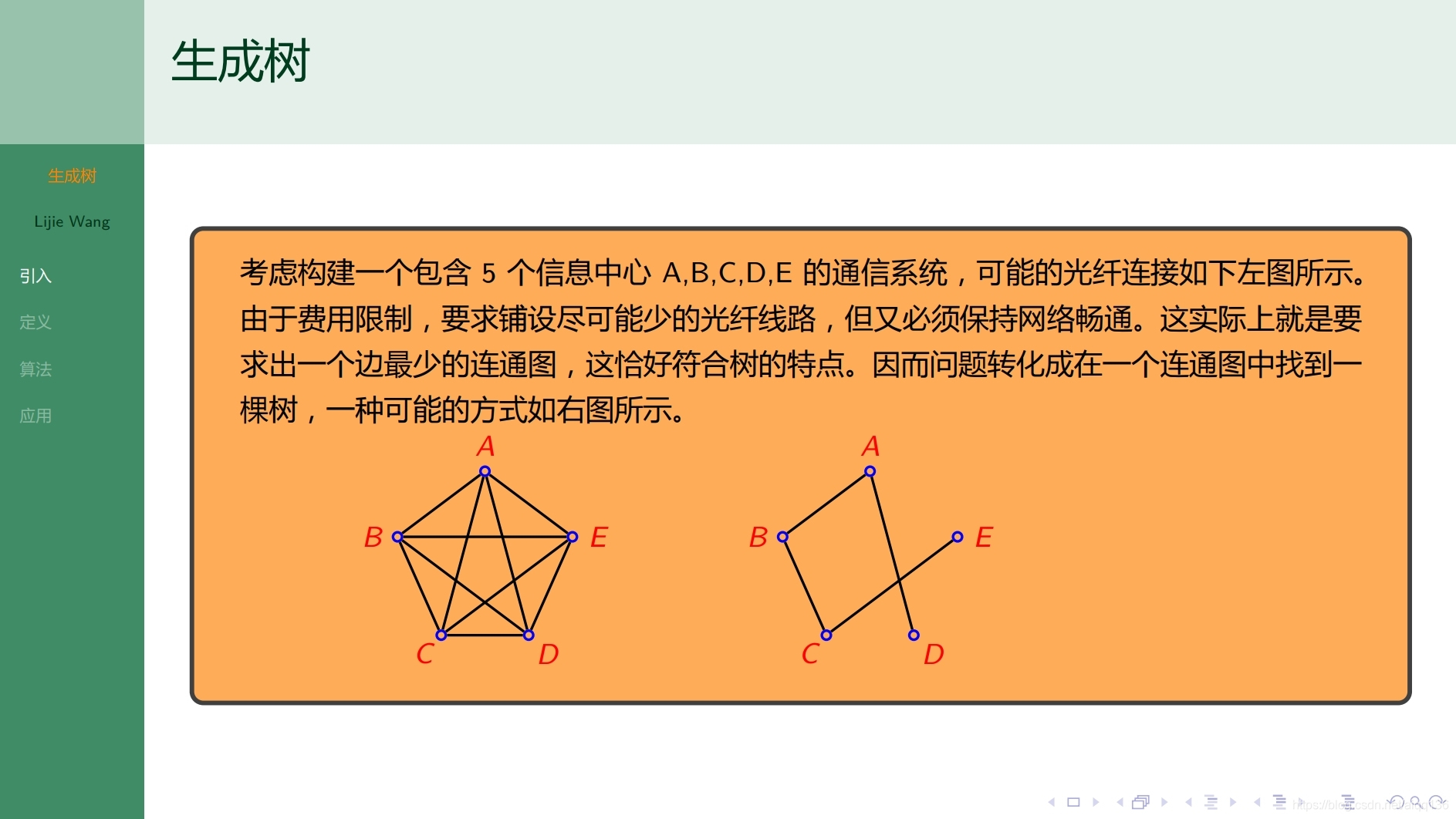
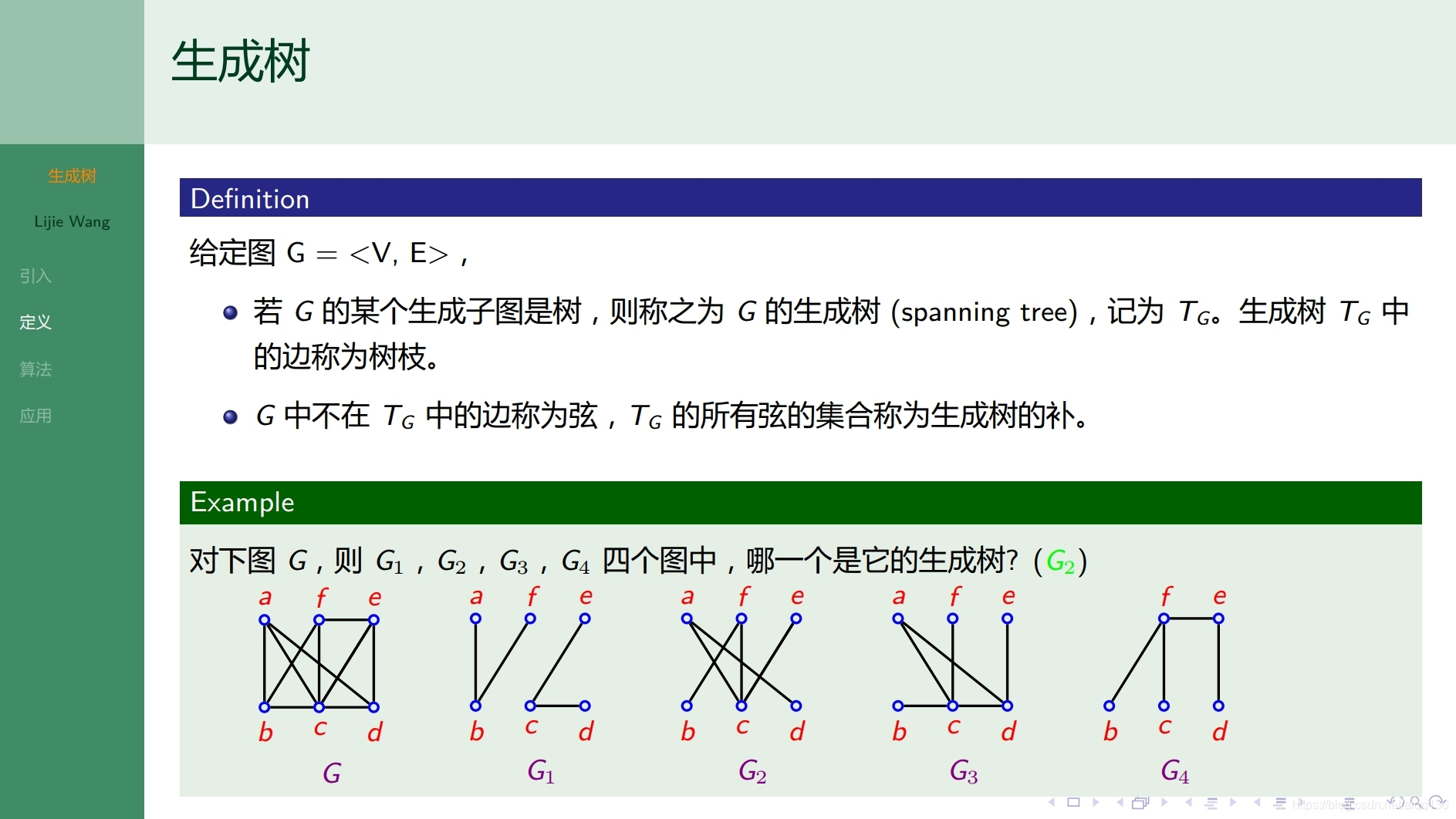
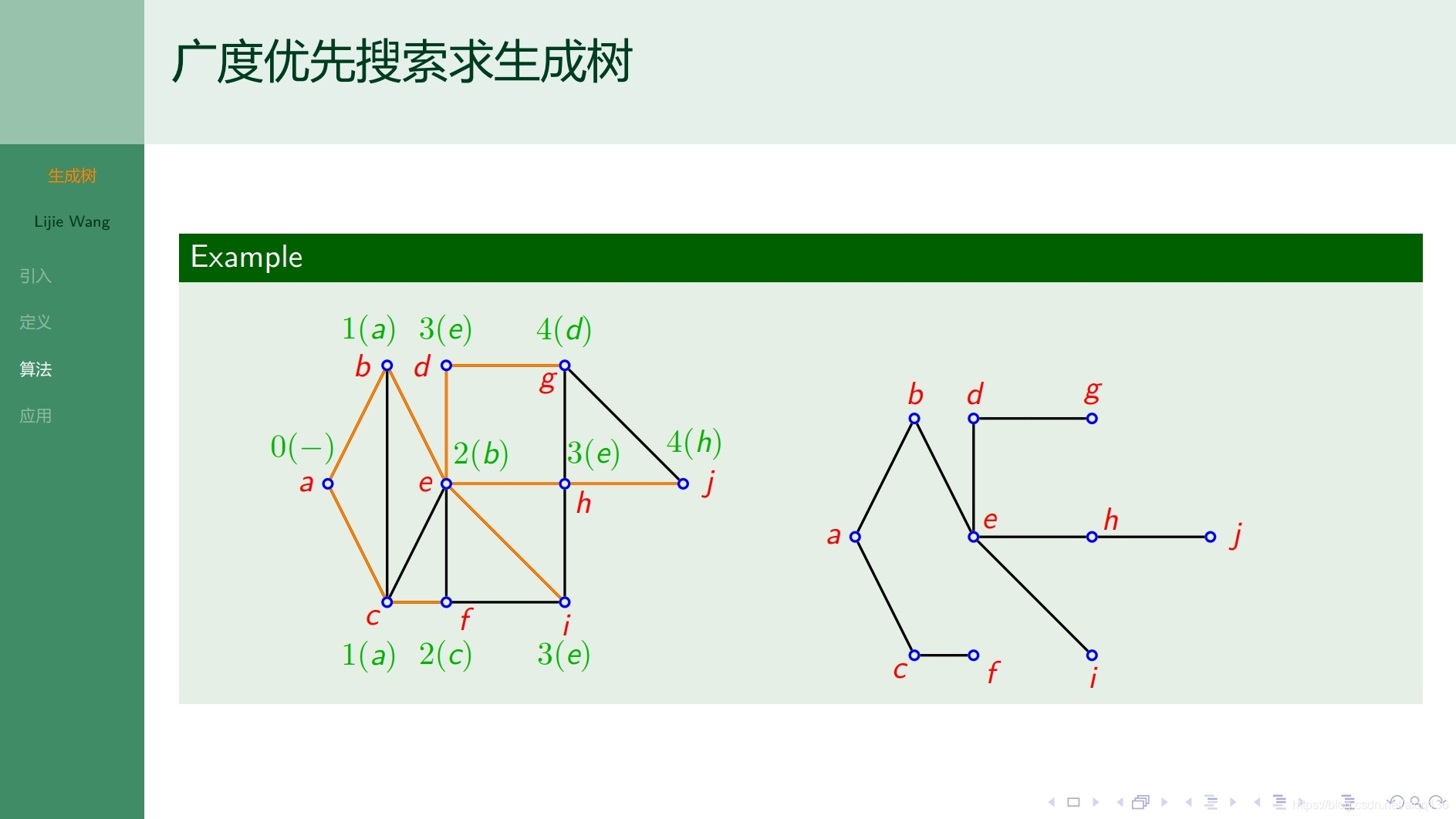
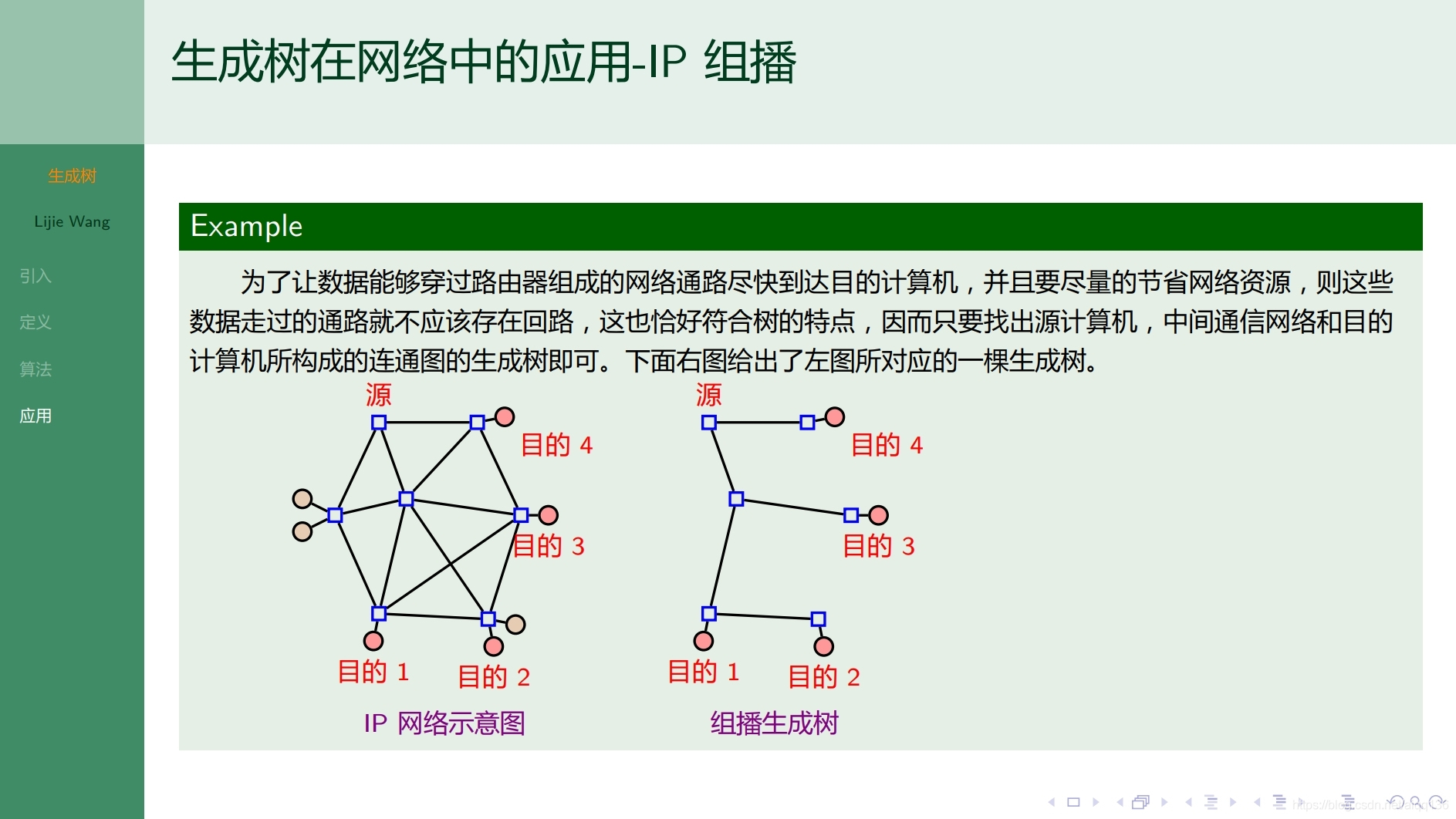
9.1.3树 生成树

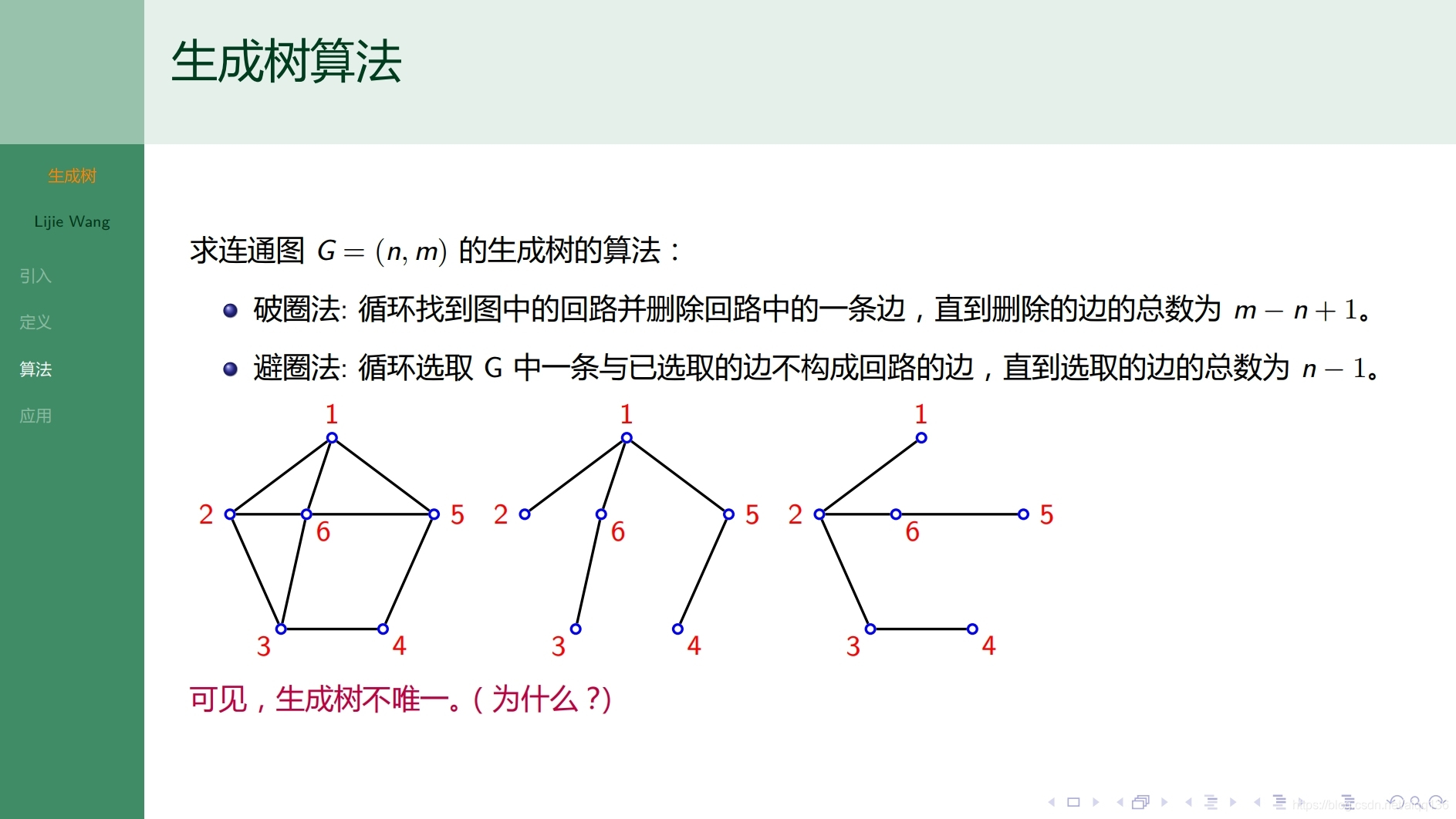
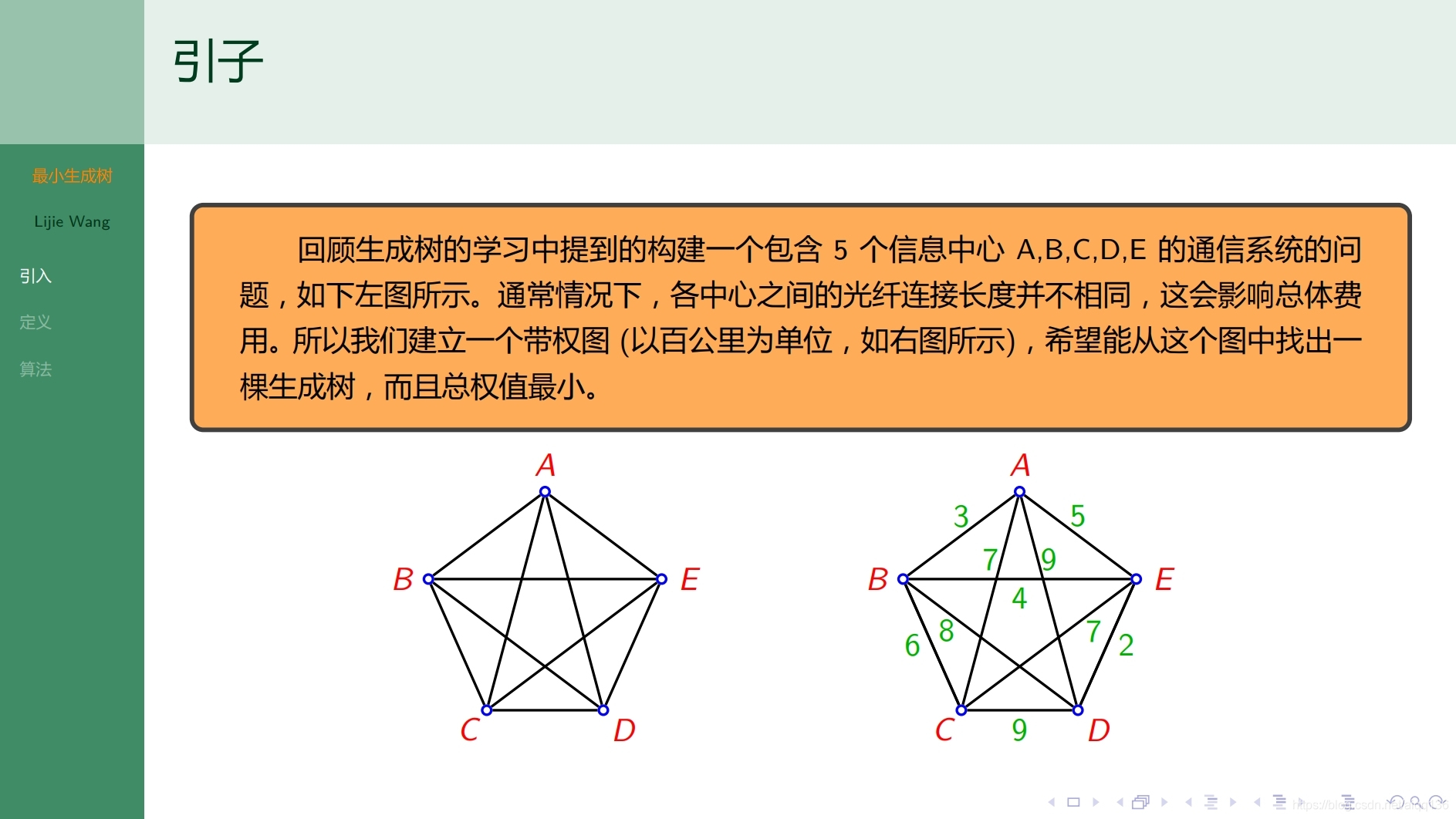
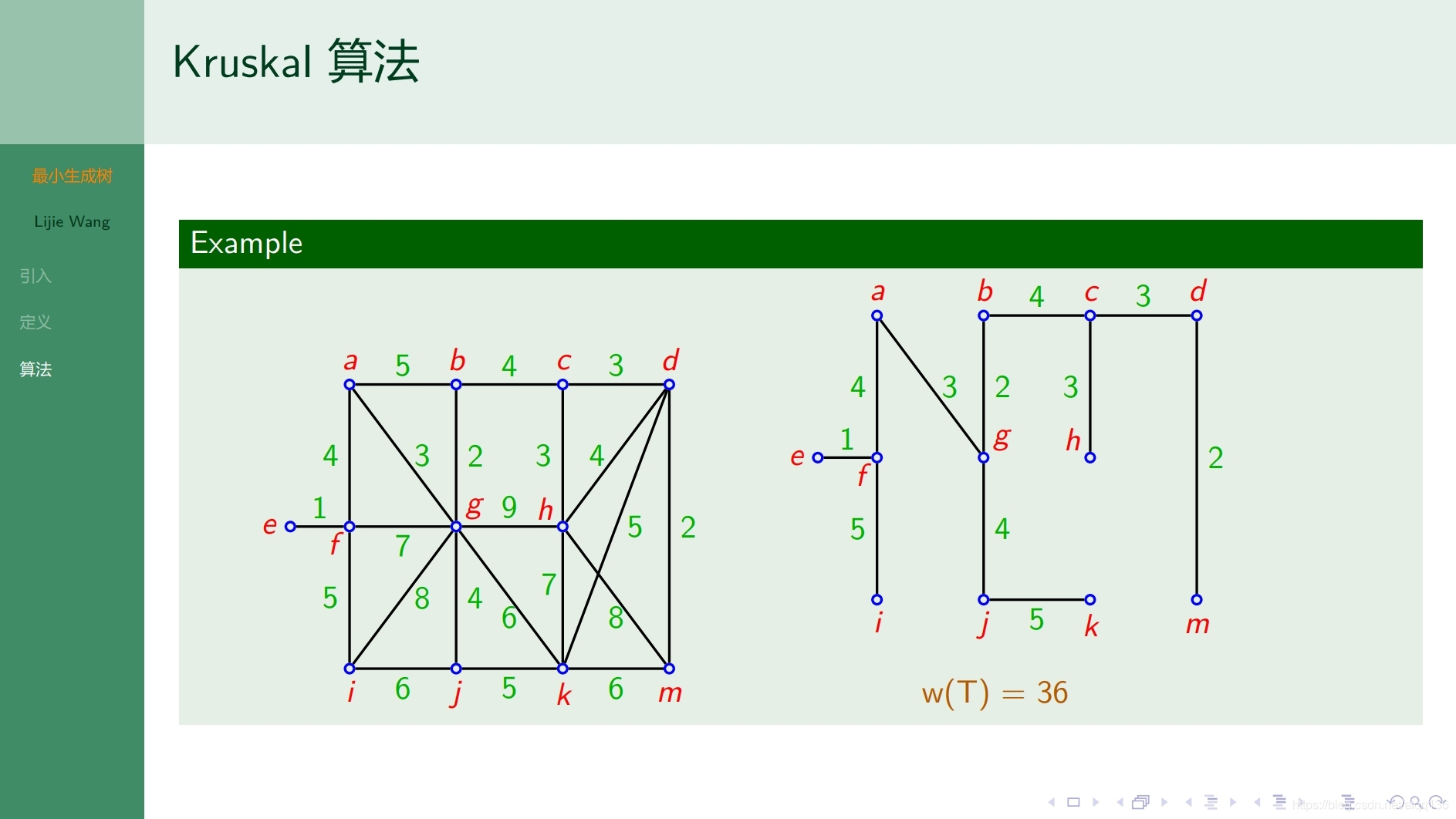
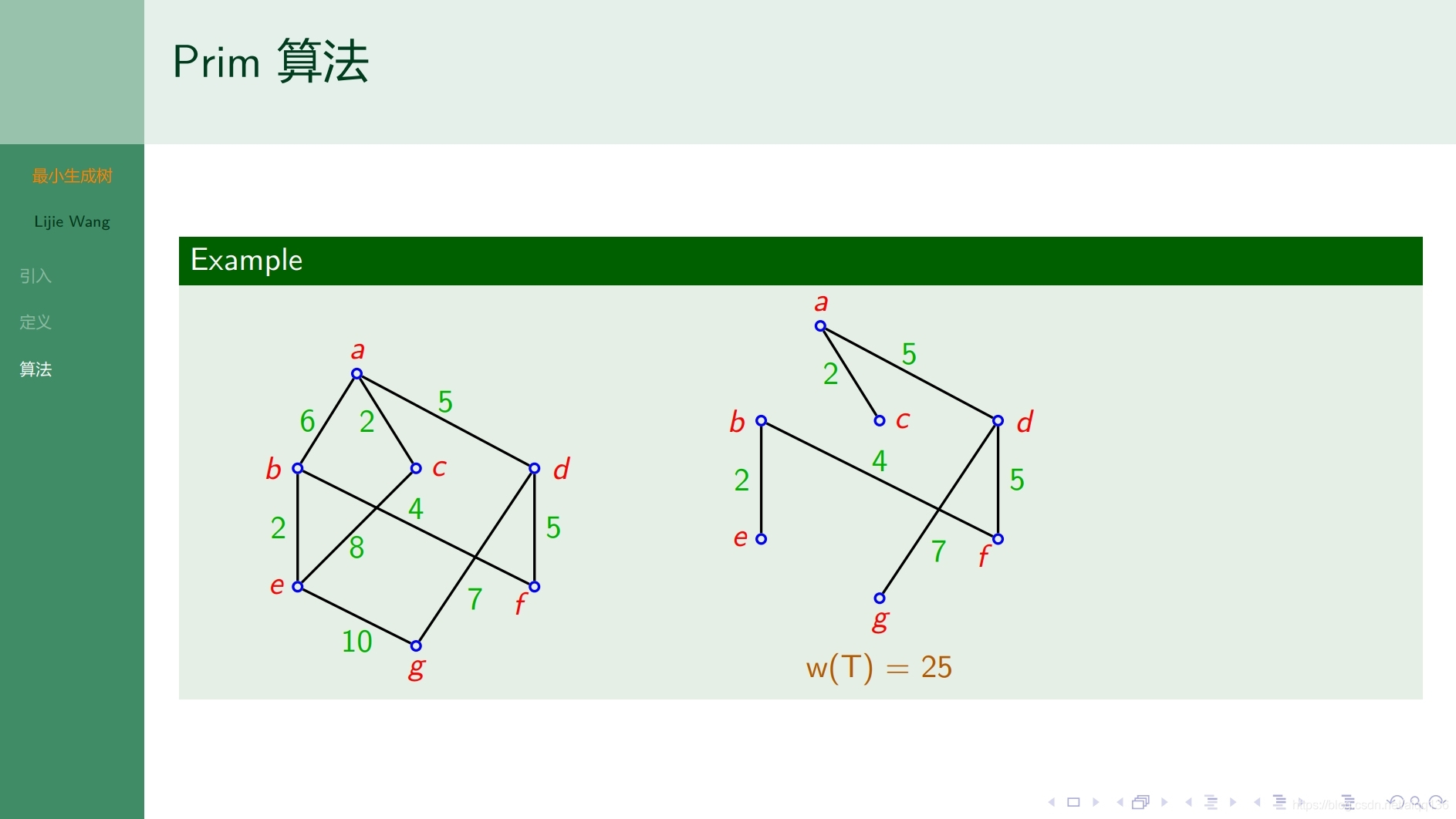
9.1.4树 最小生成树

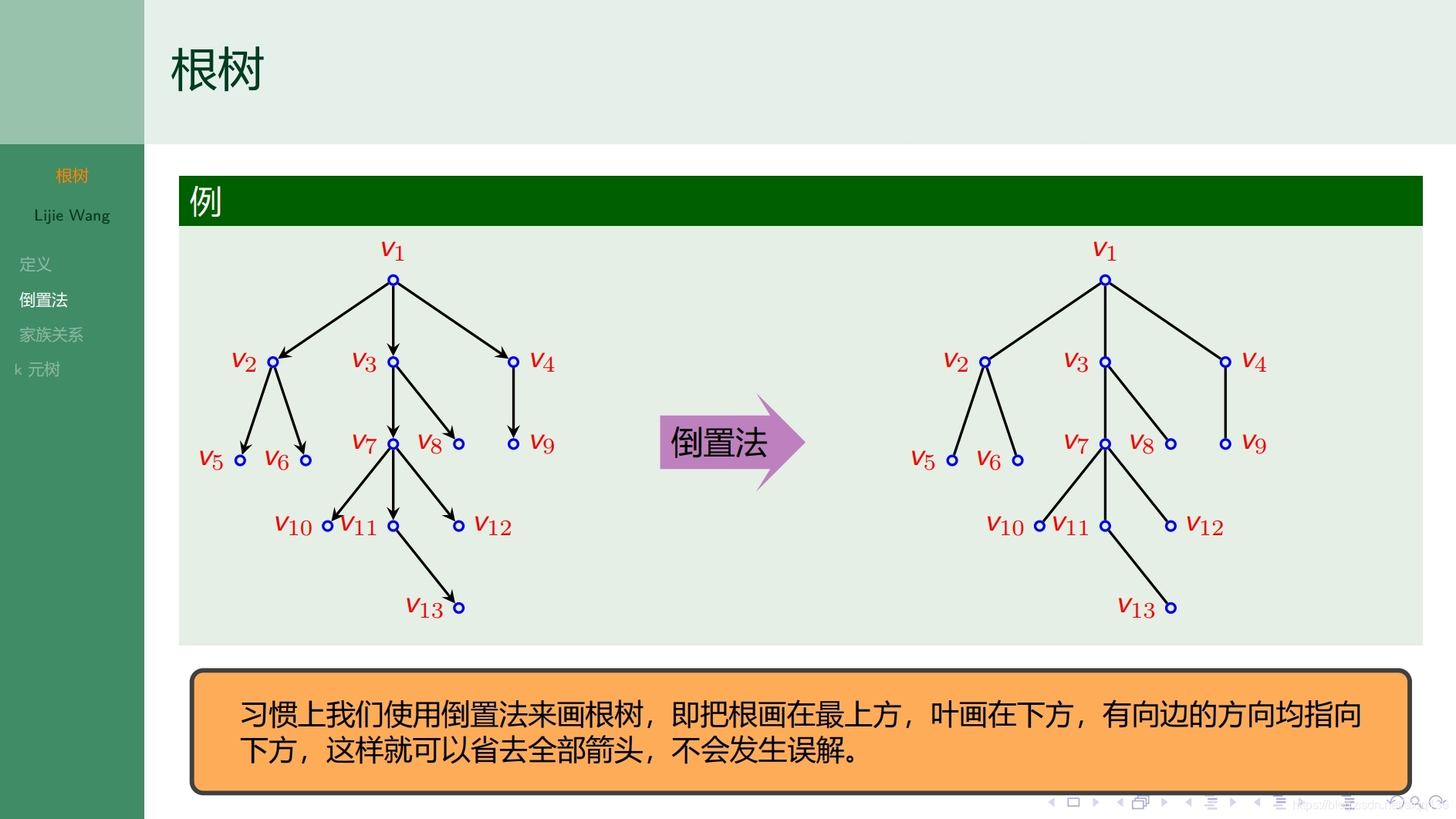
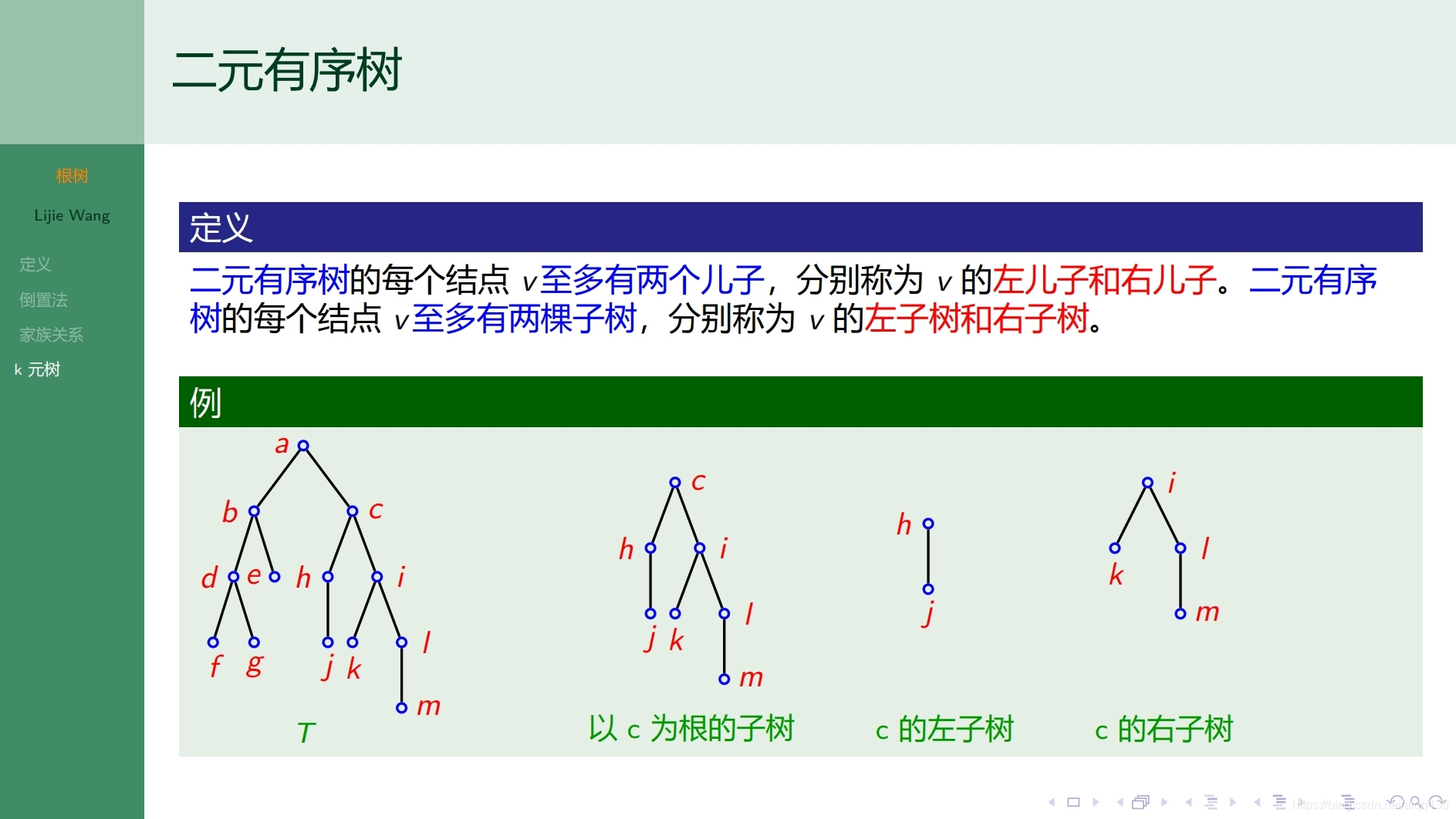
9.2.1树 根树

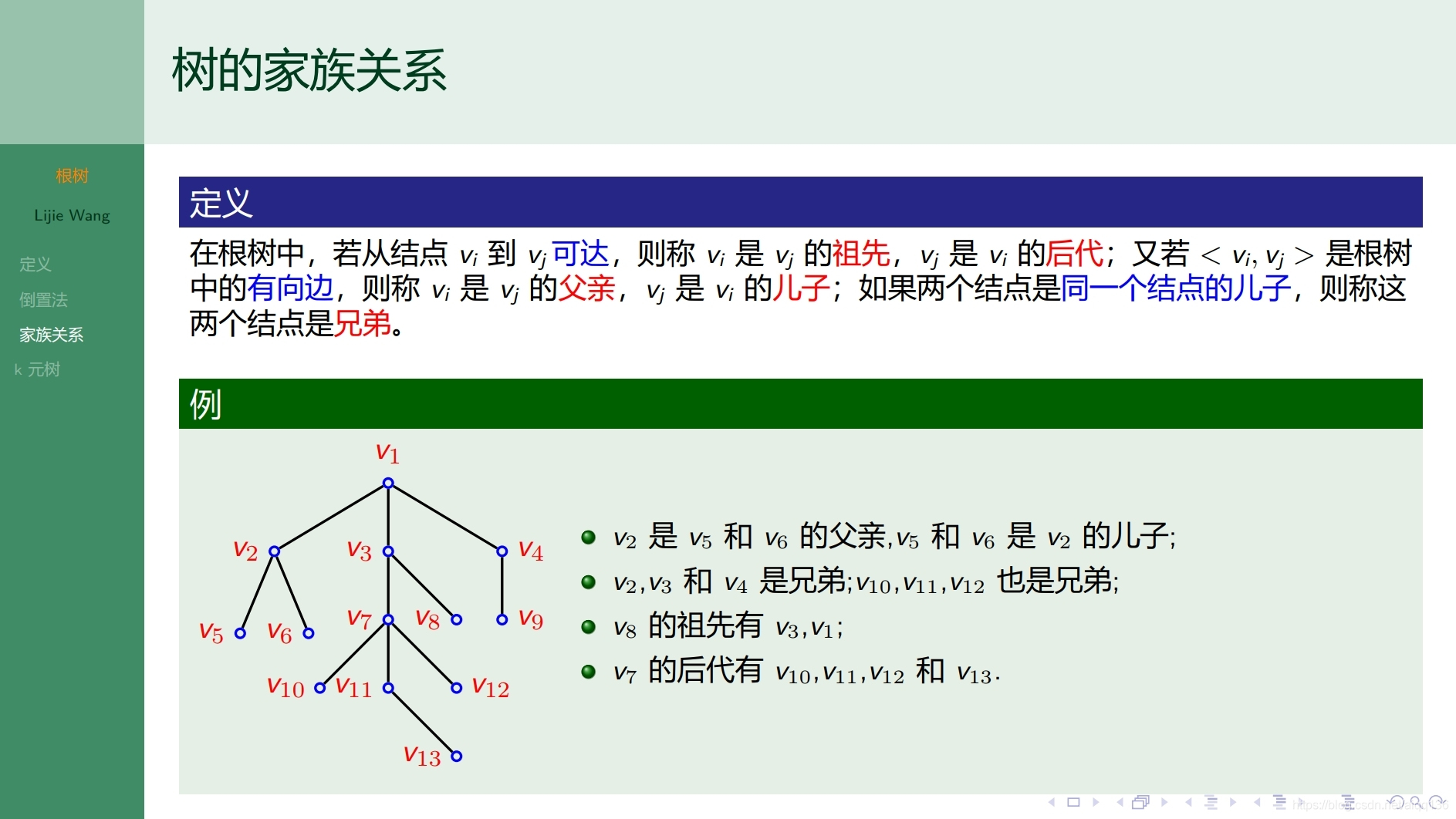
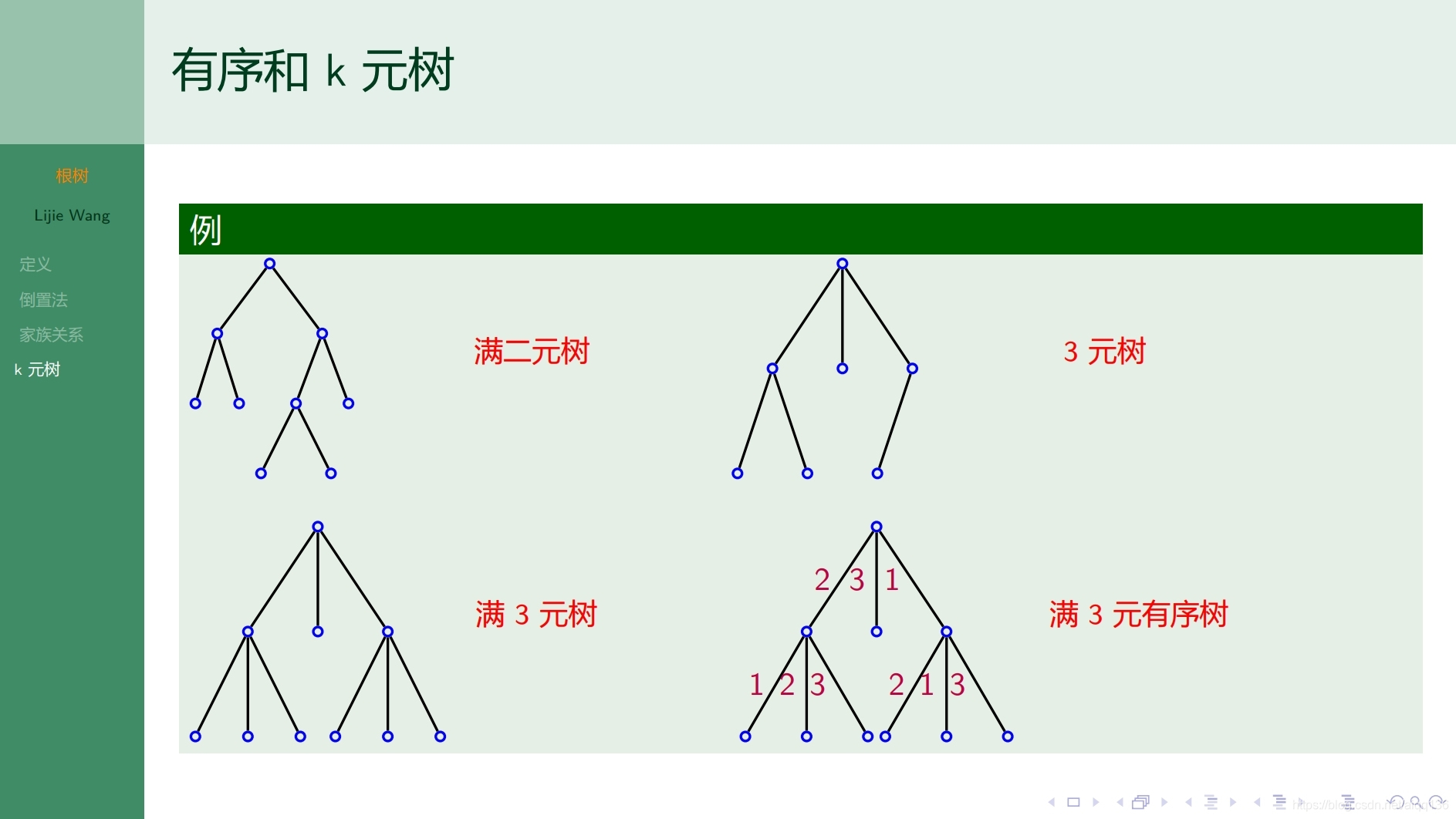
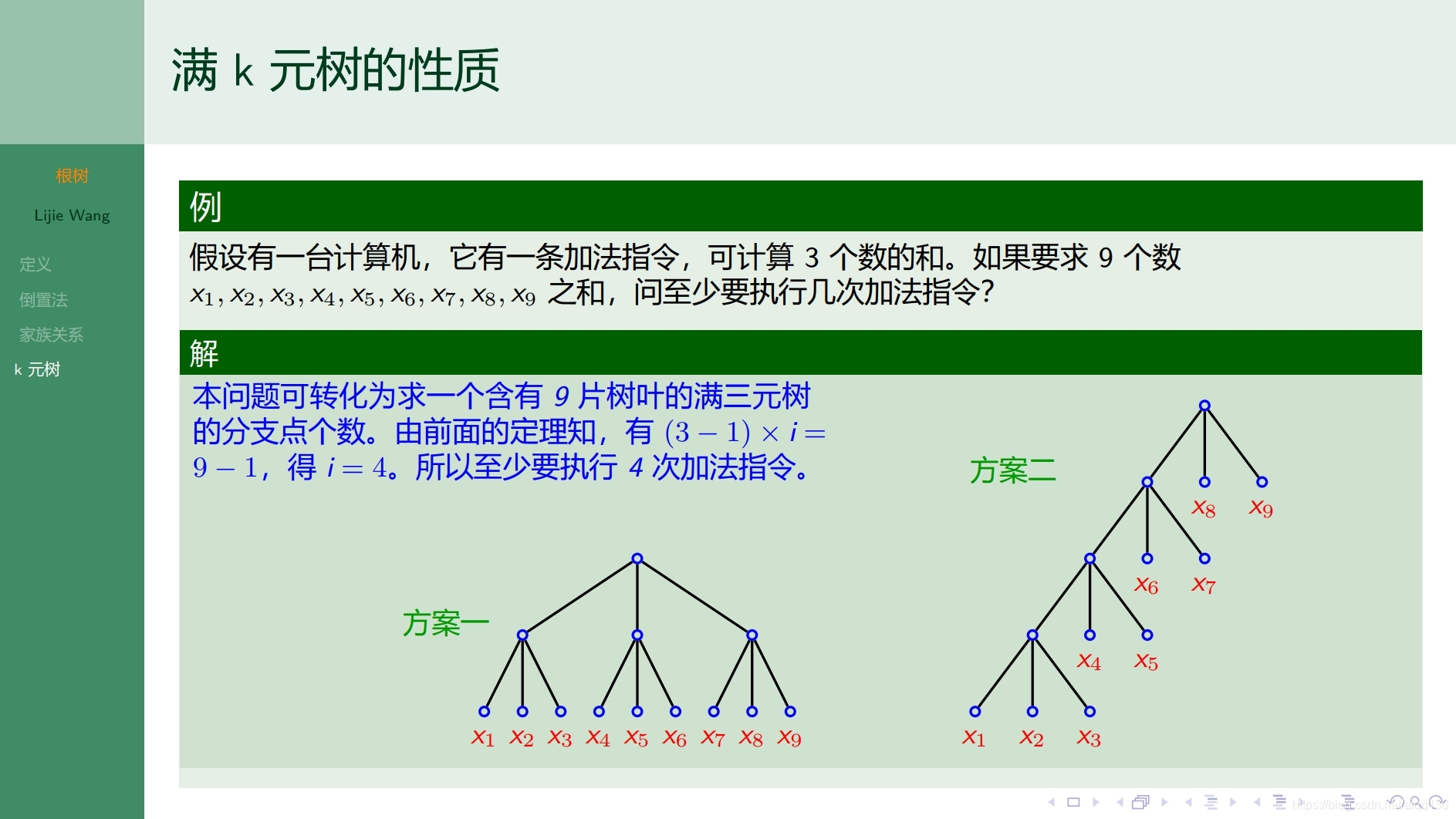
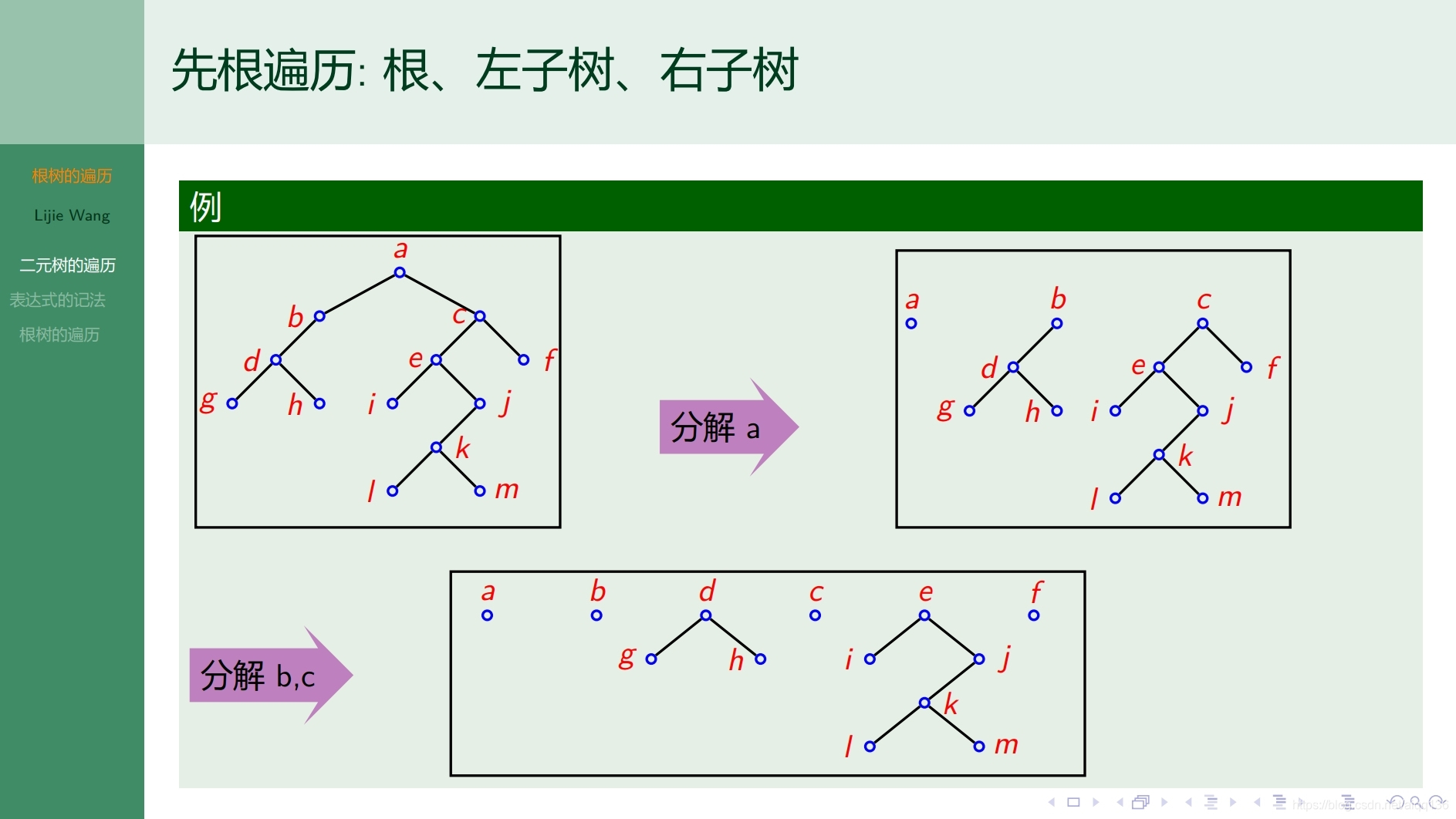
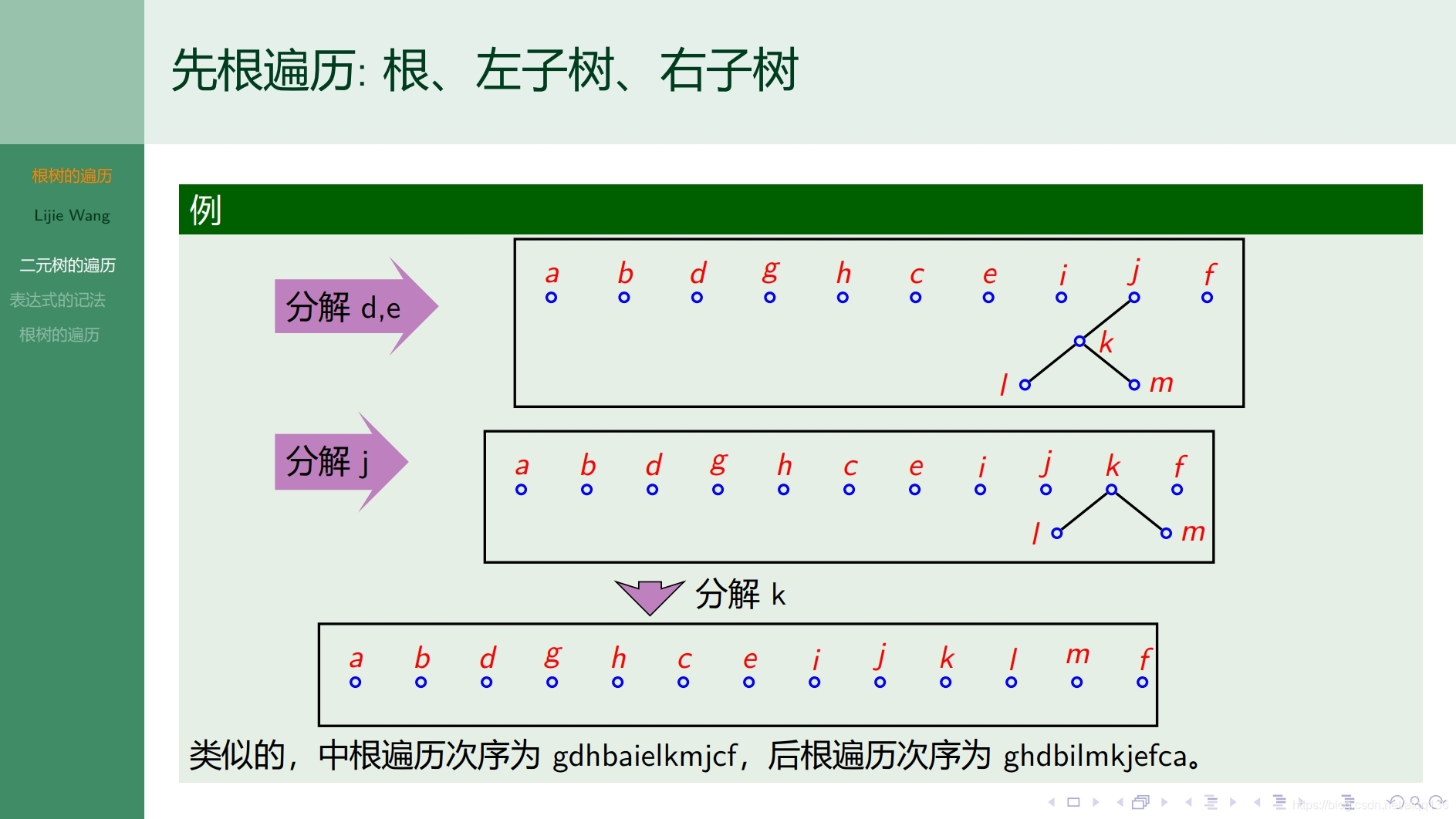
9.2.2树 根树的遍历

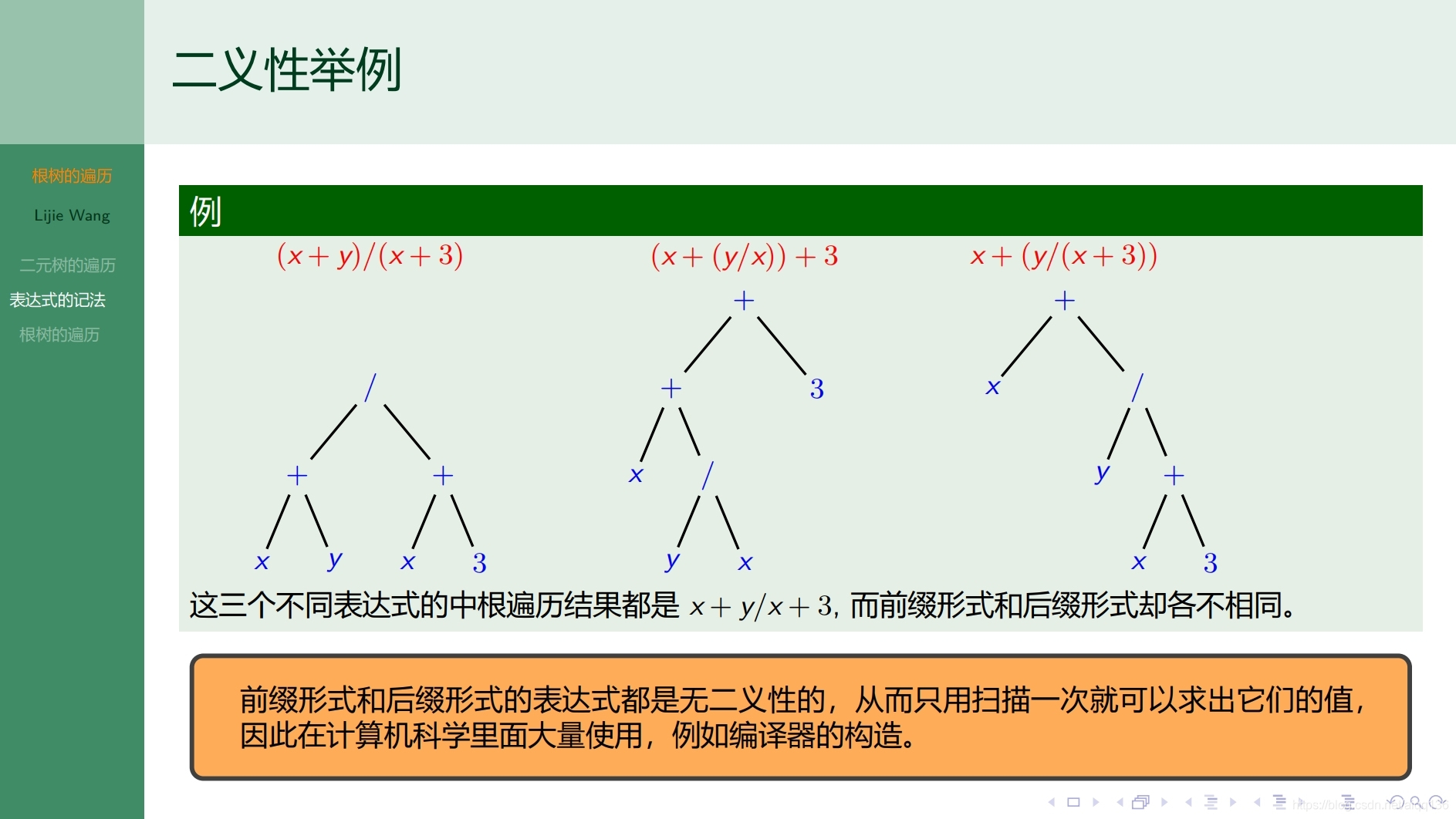
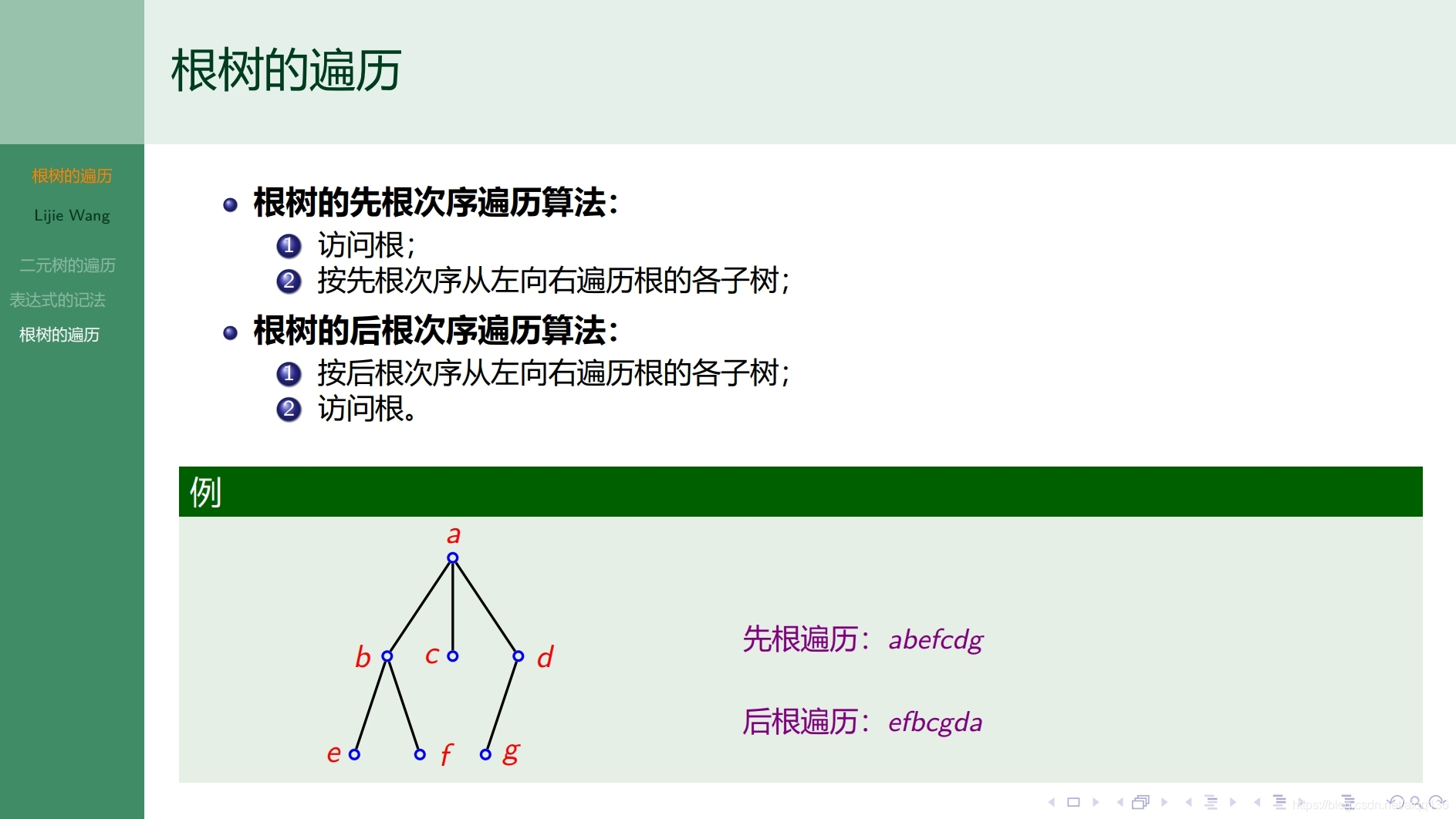
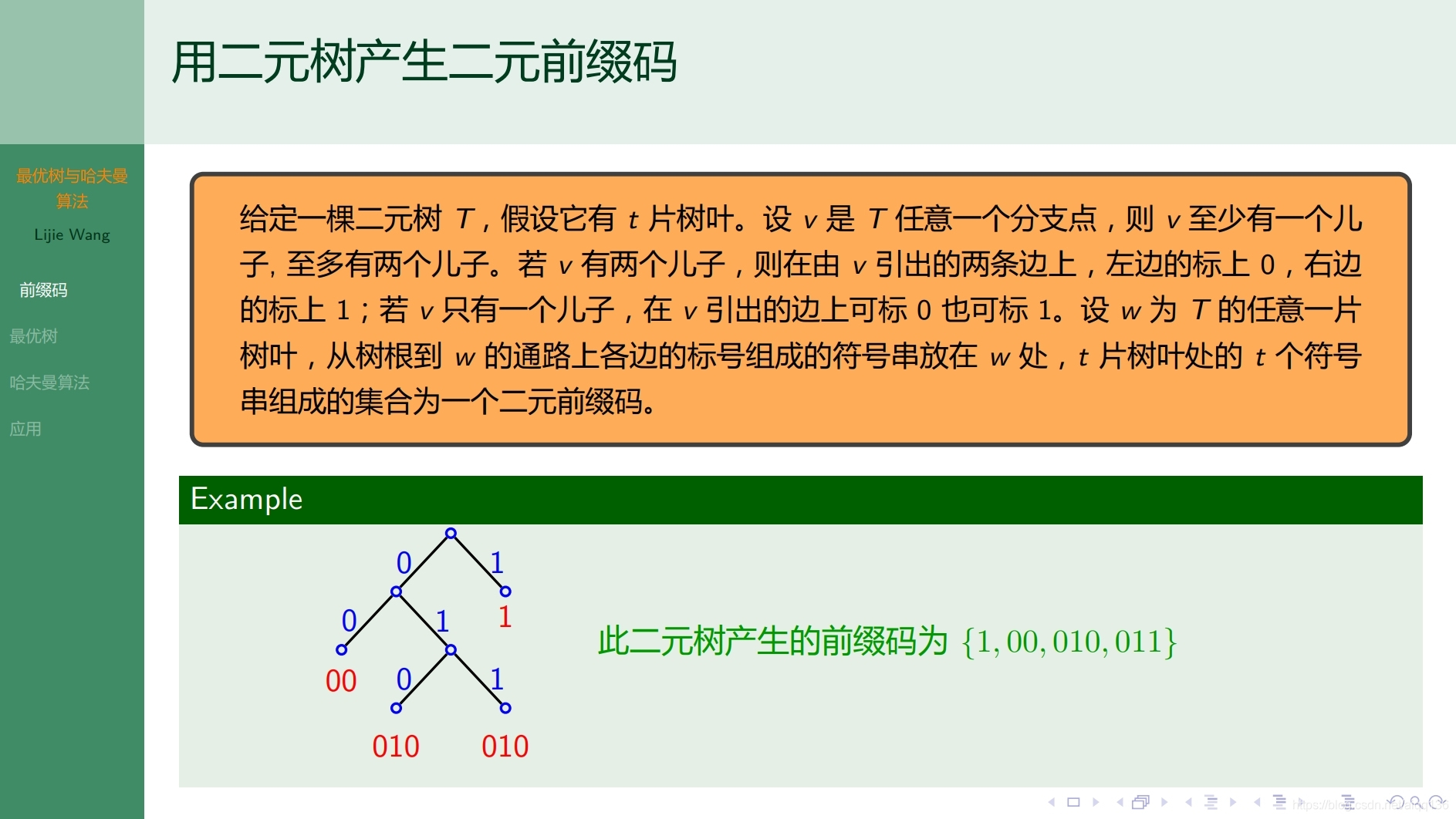
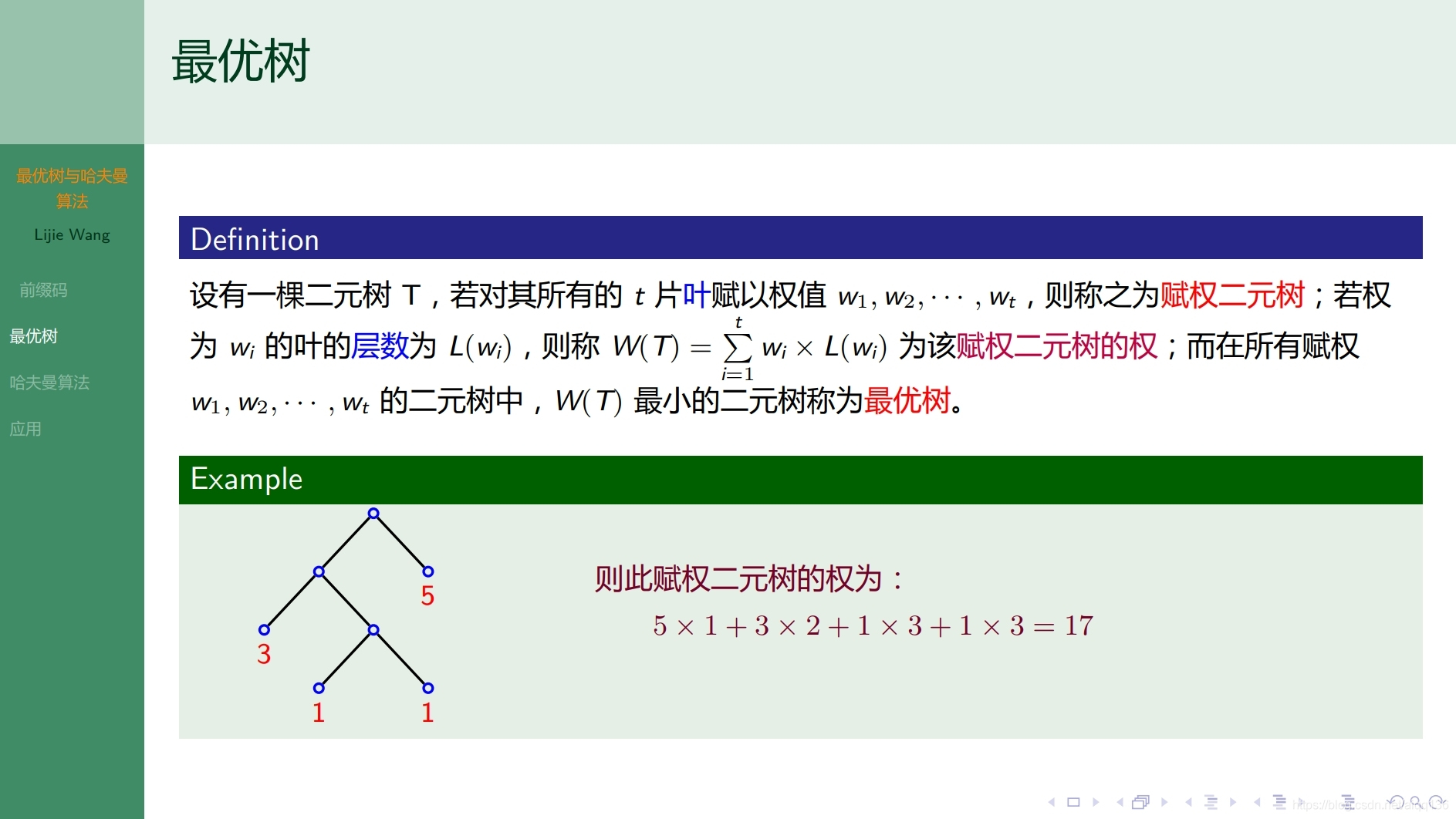
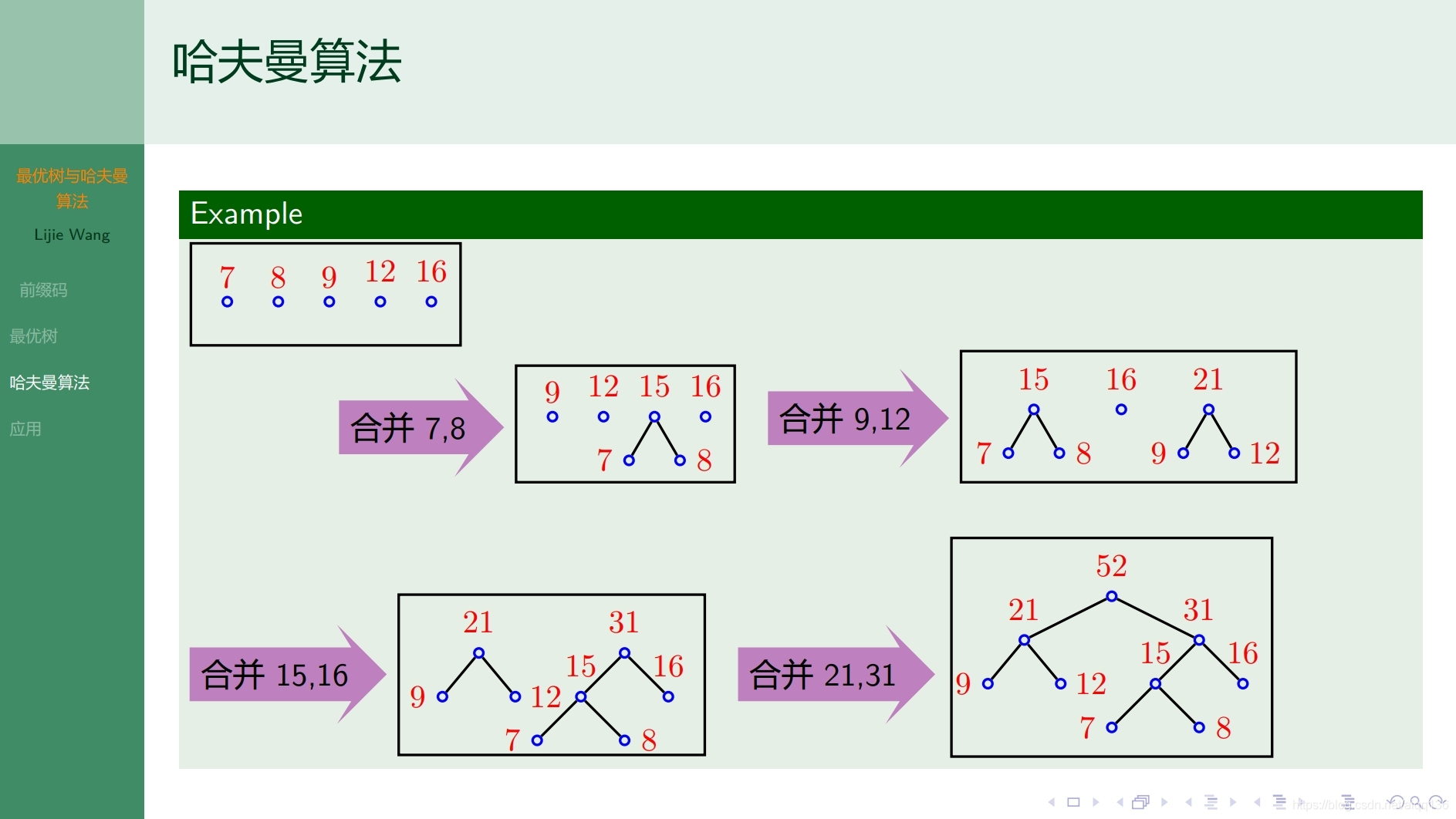
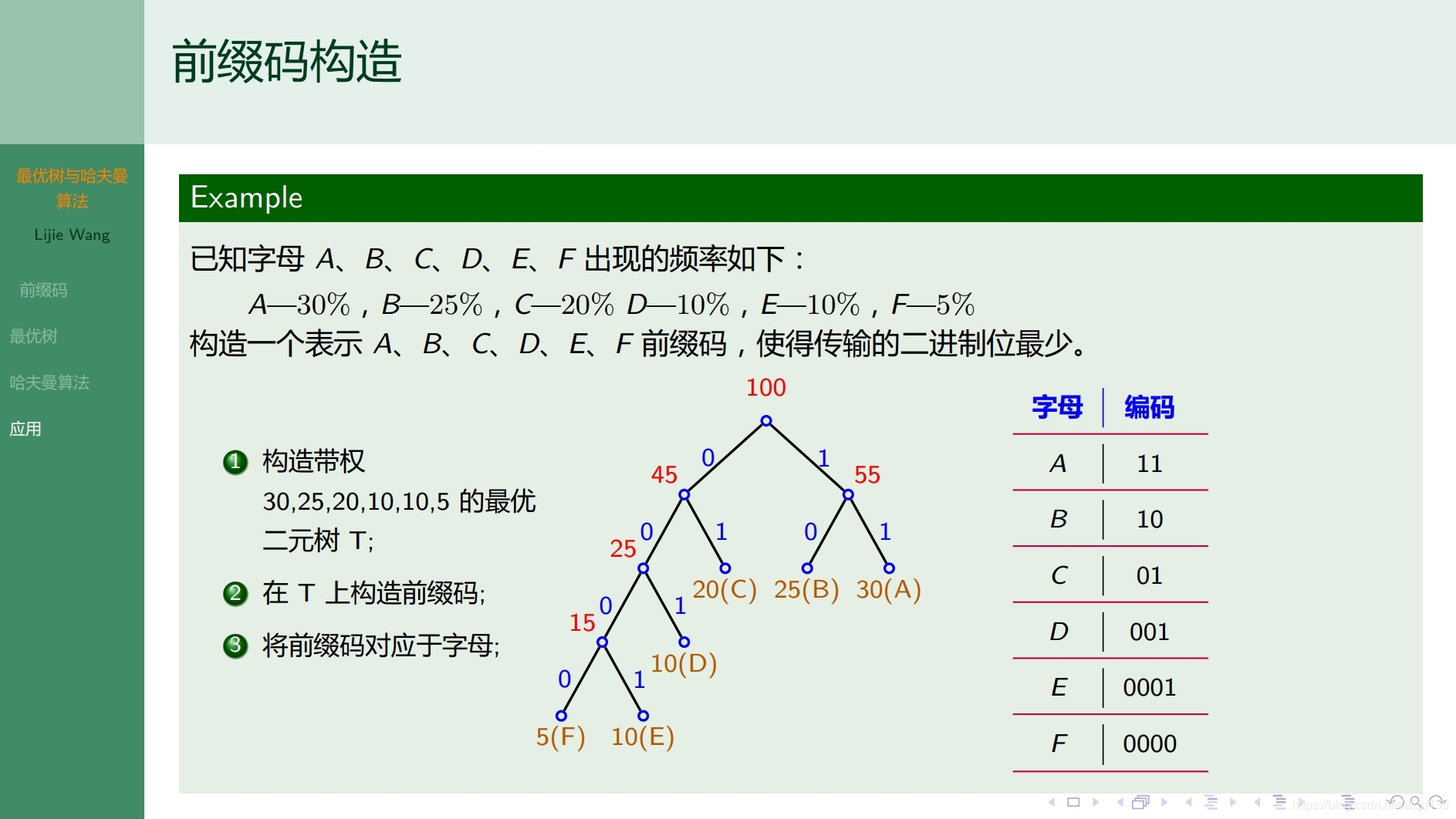
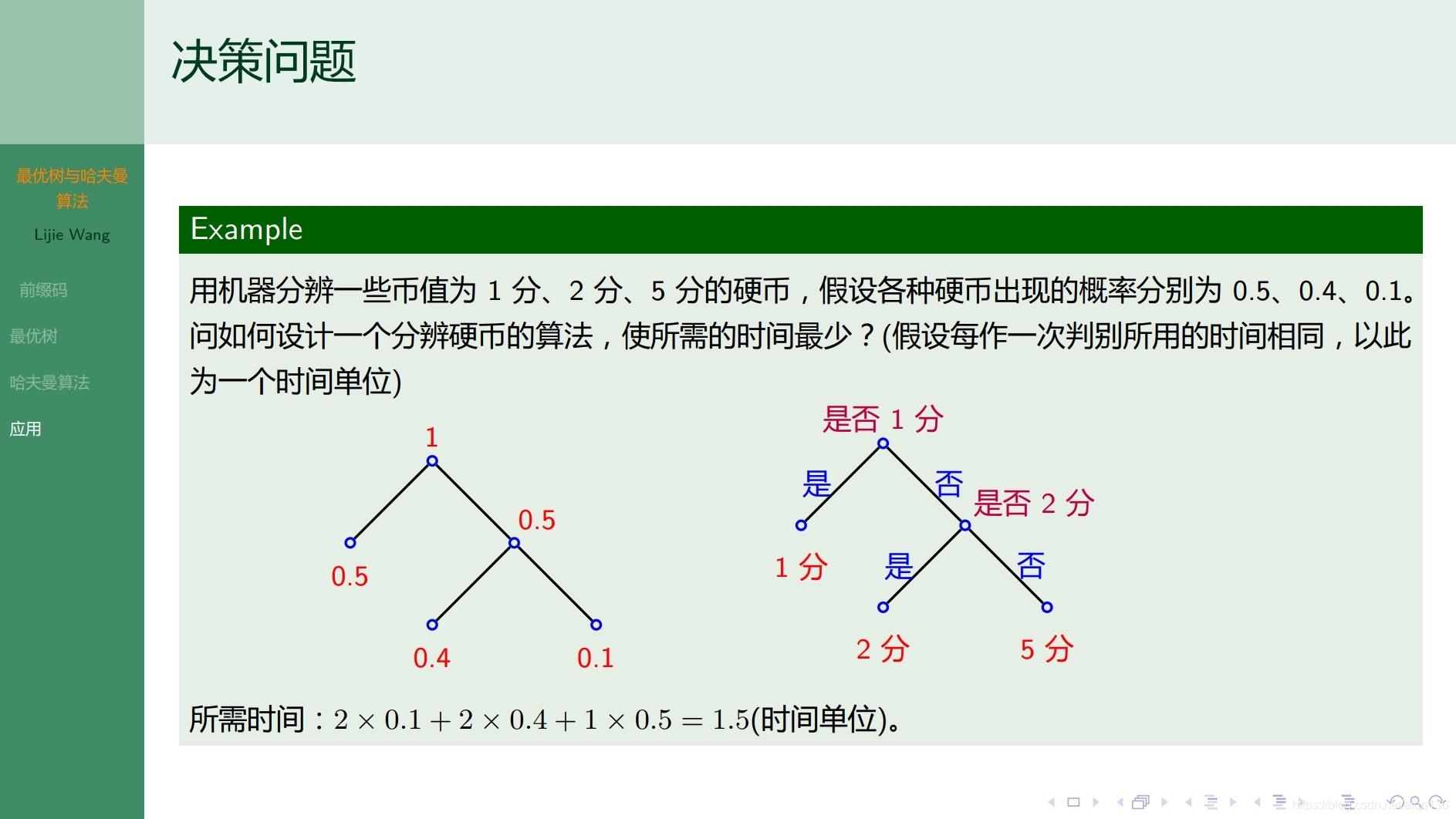
9.2.3树 最优树和哈夫曼算法

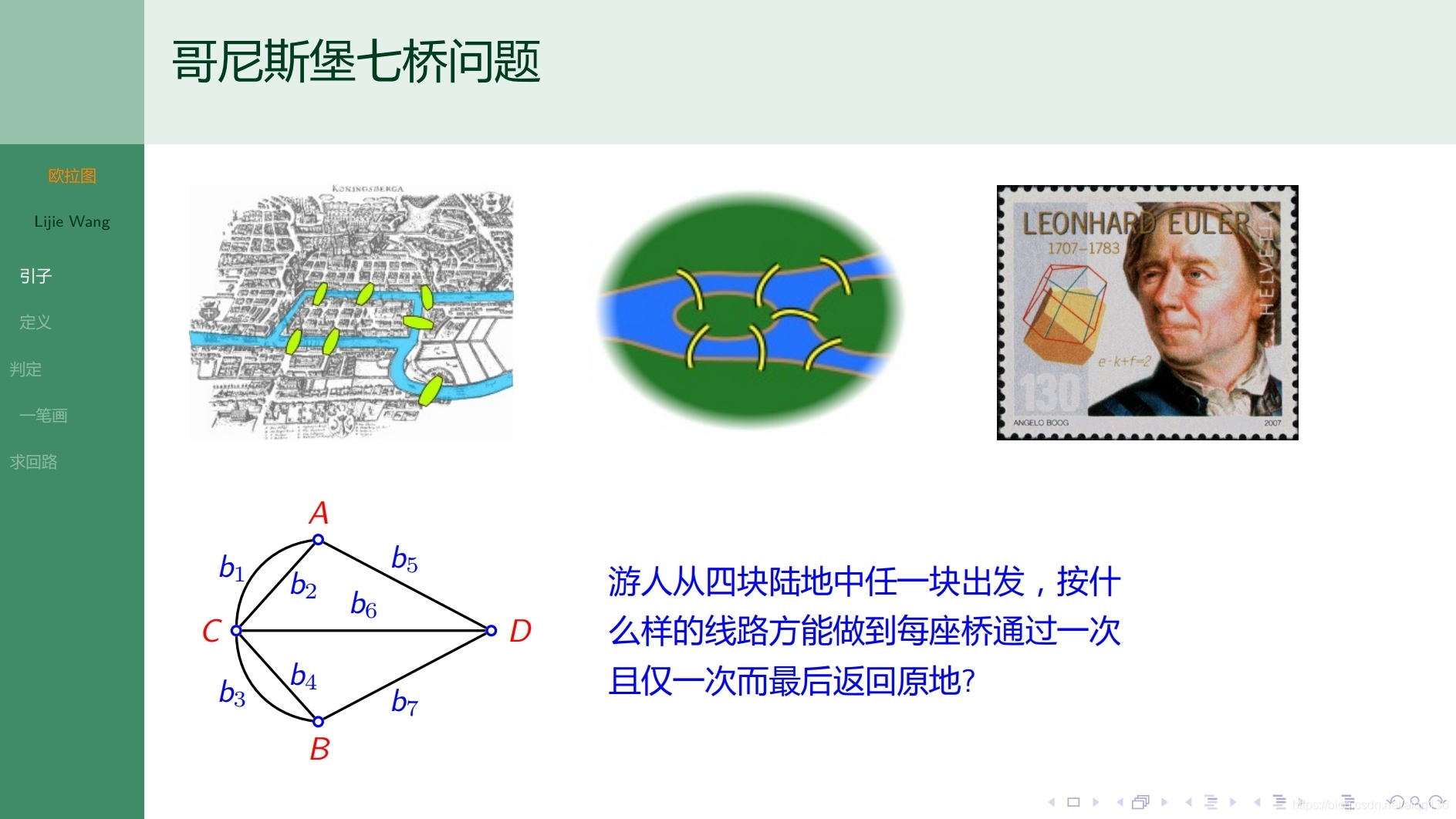
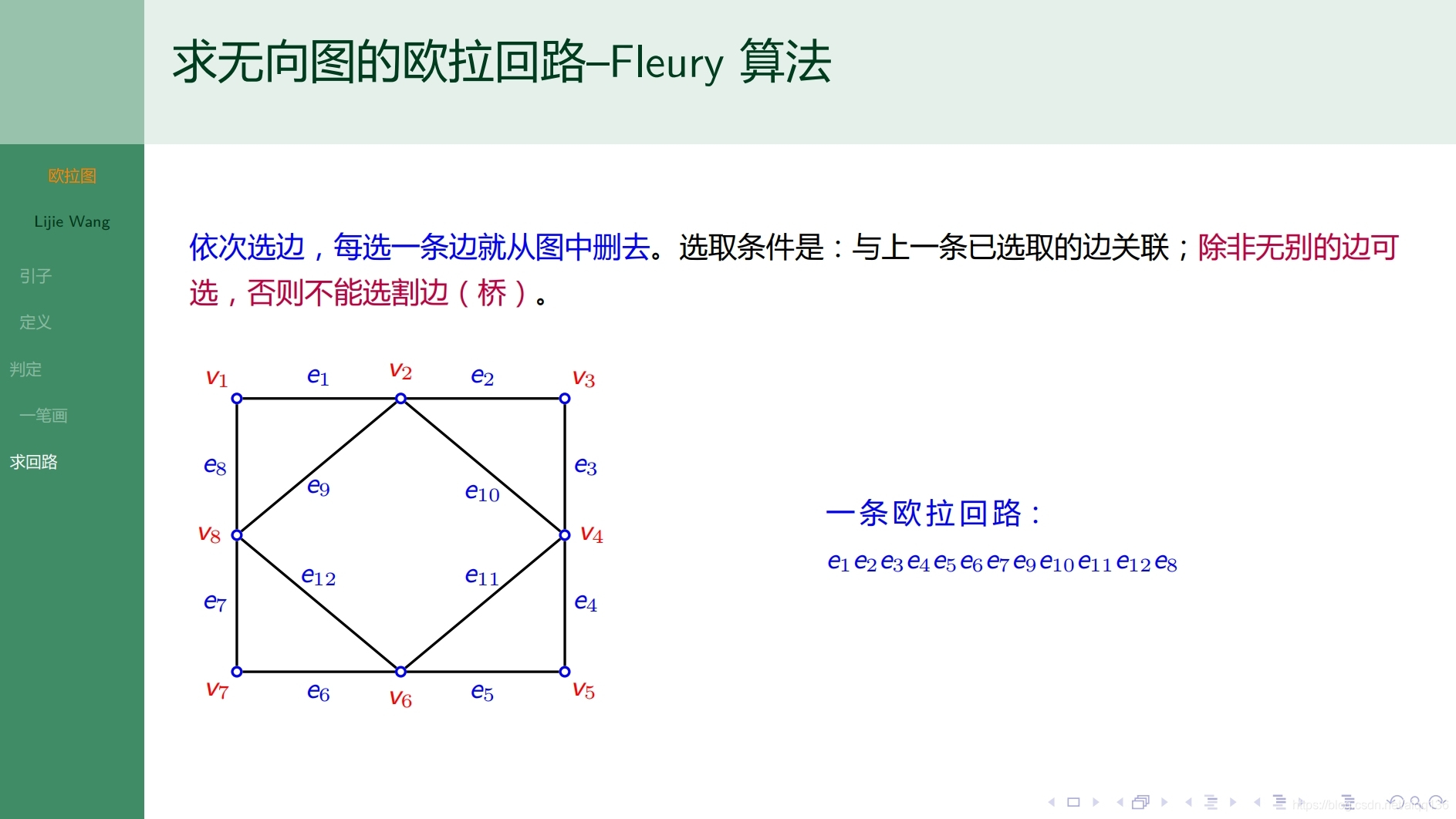
10.1.1特殊图 欧拉图

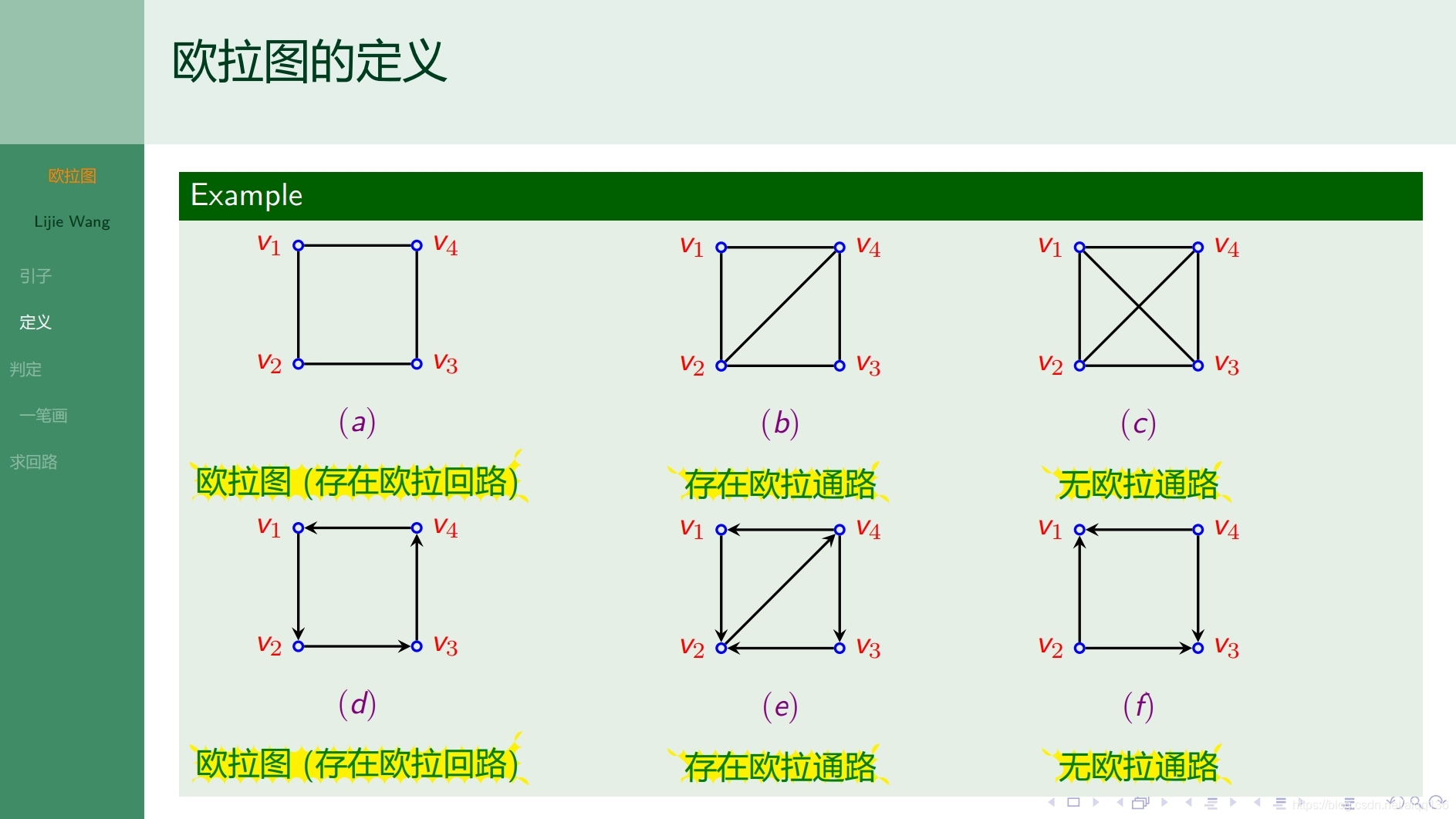
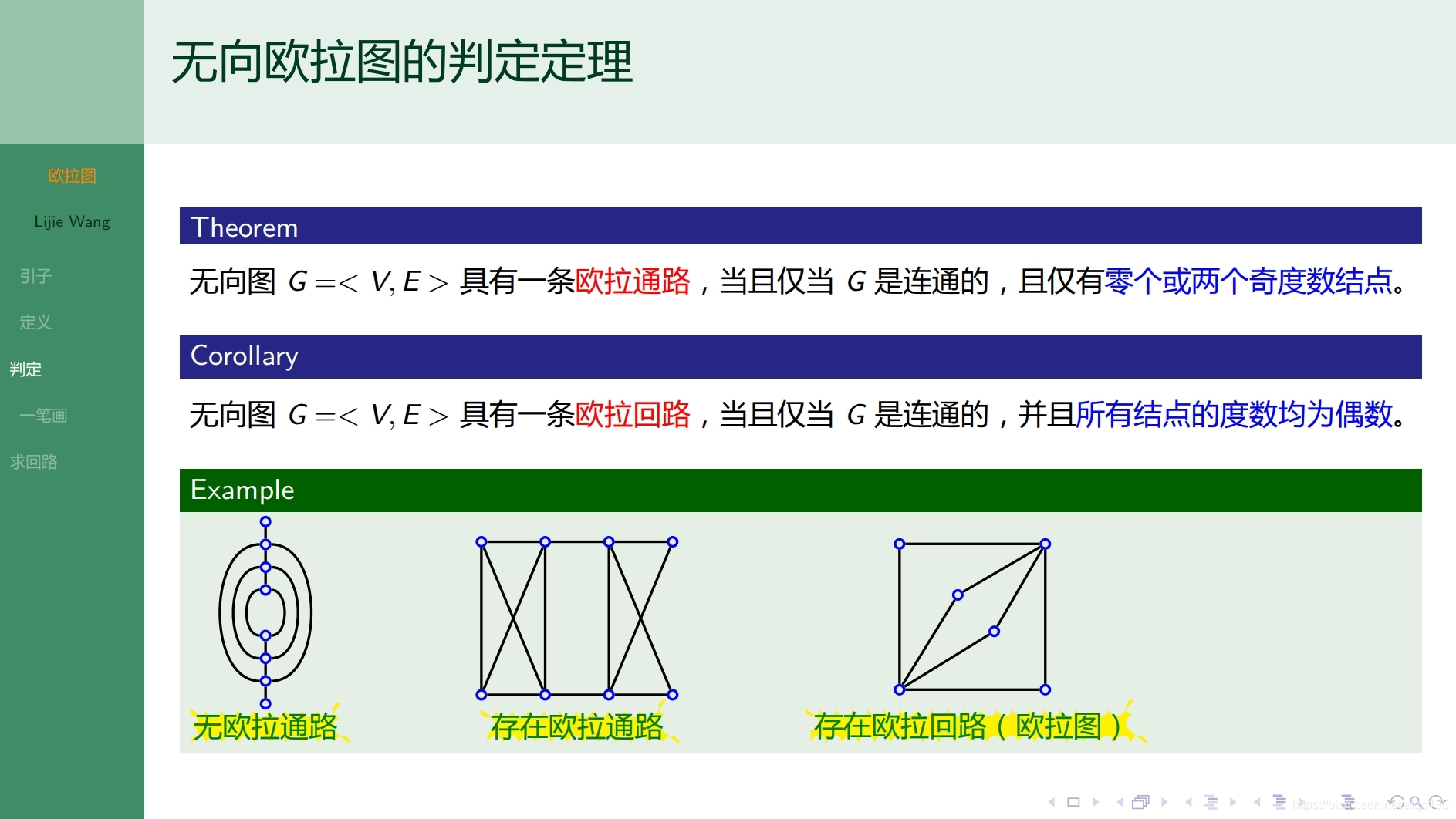
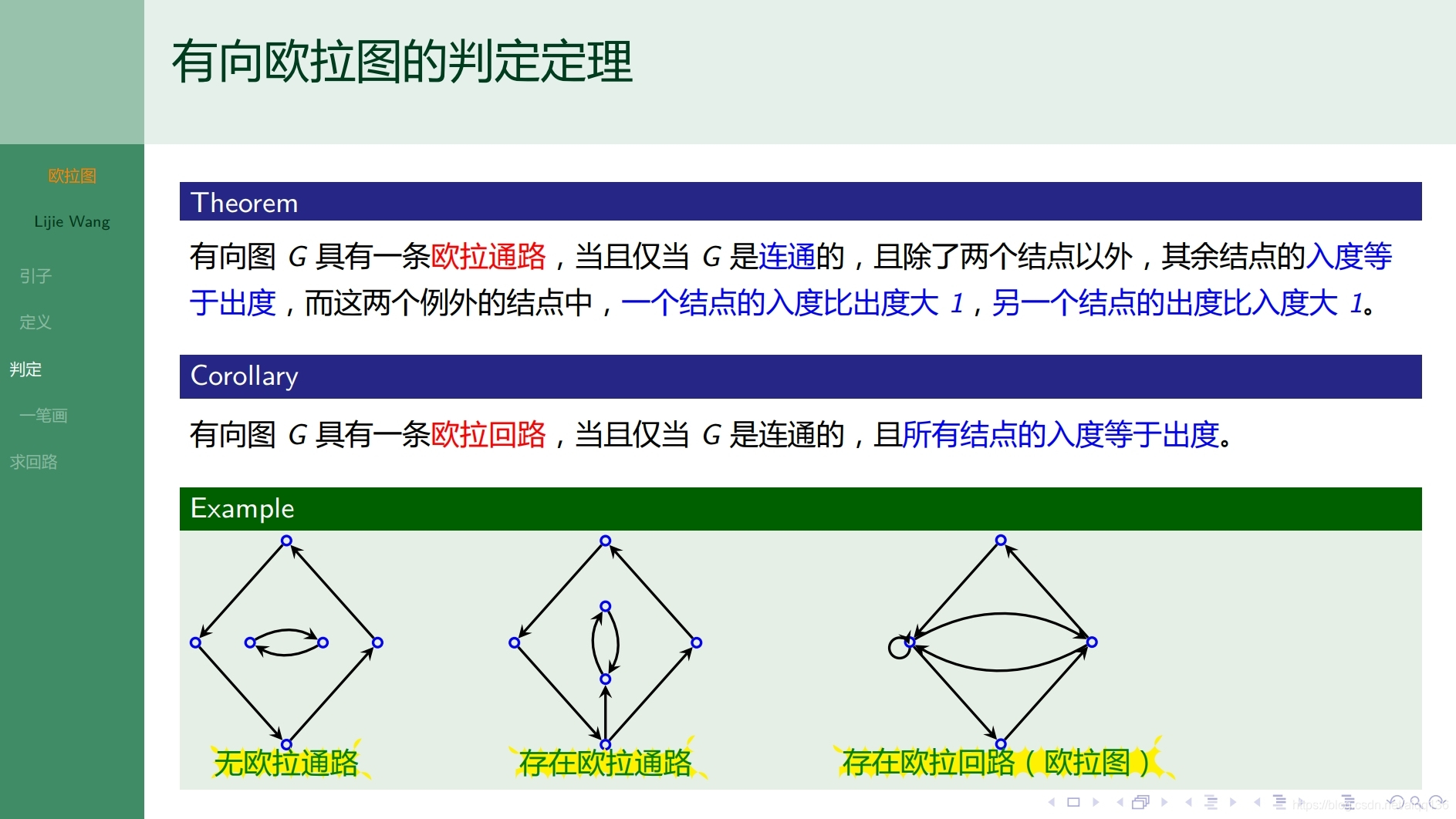
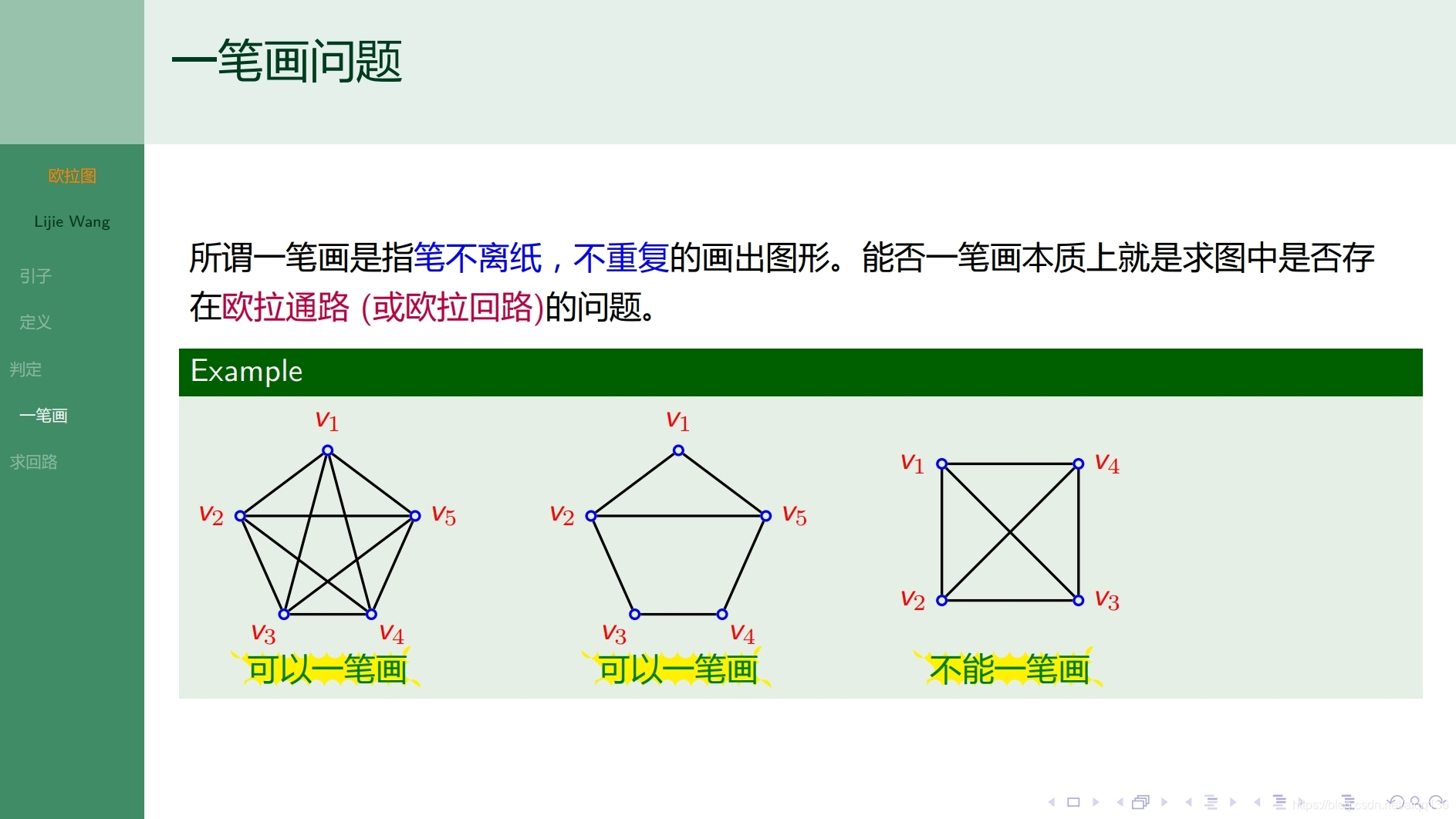
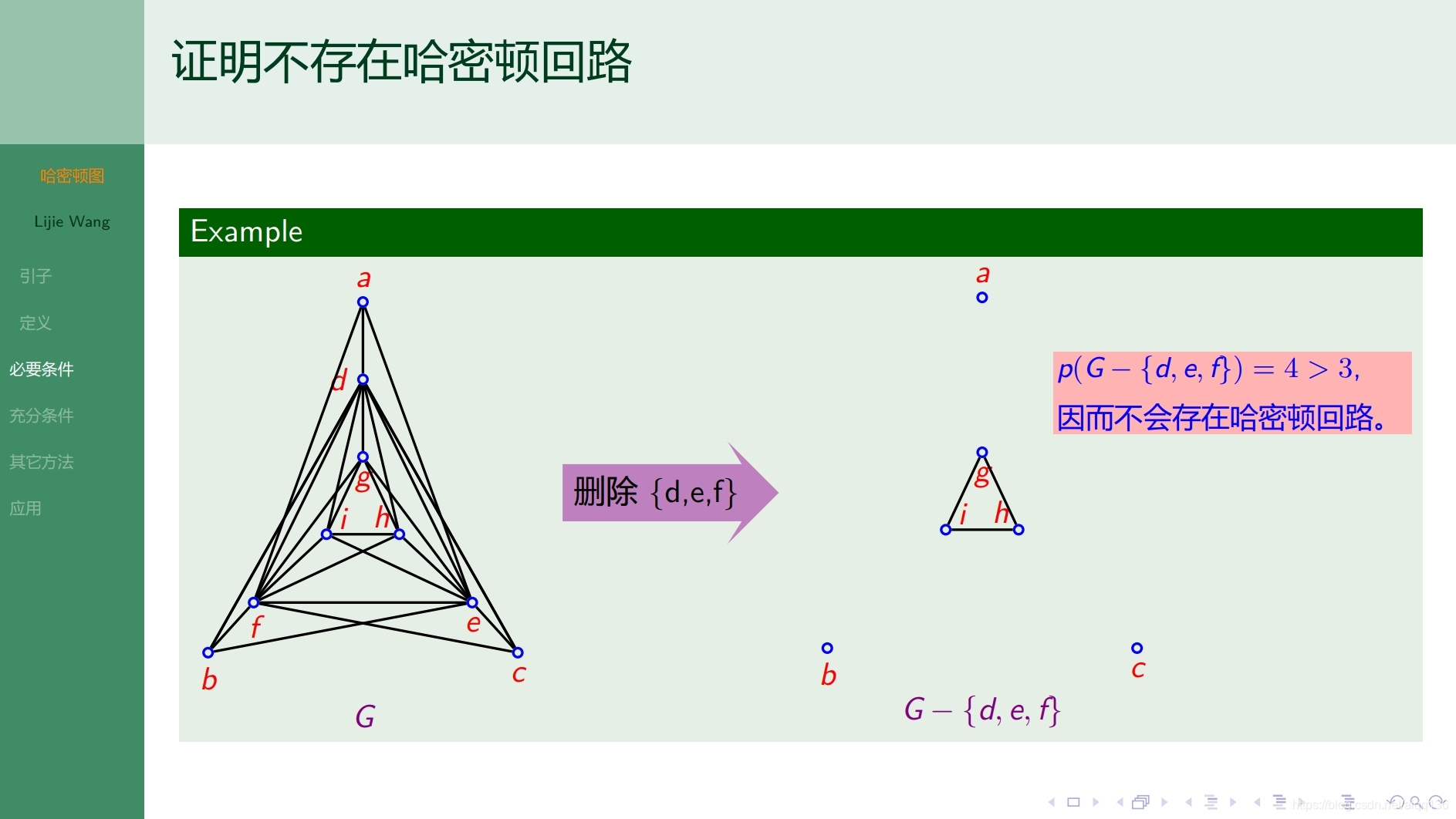
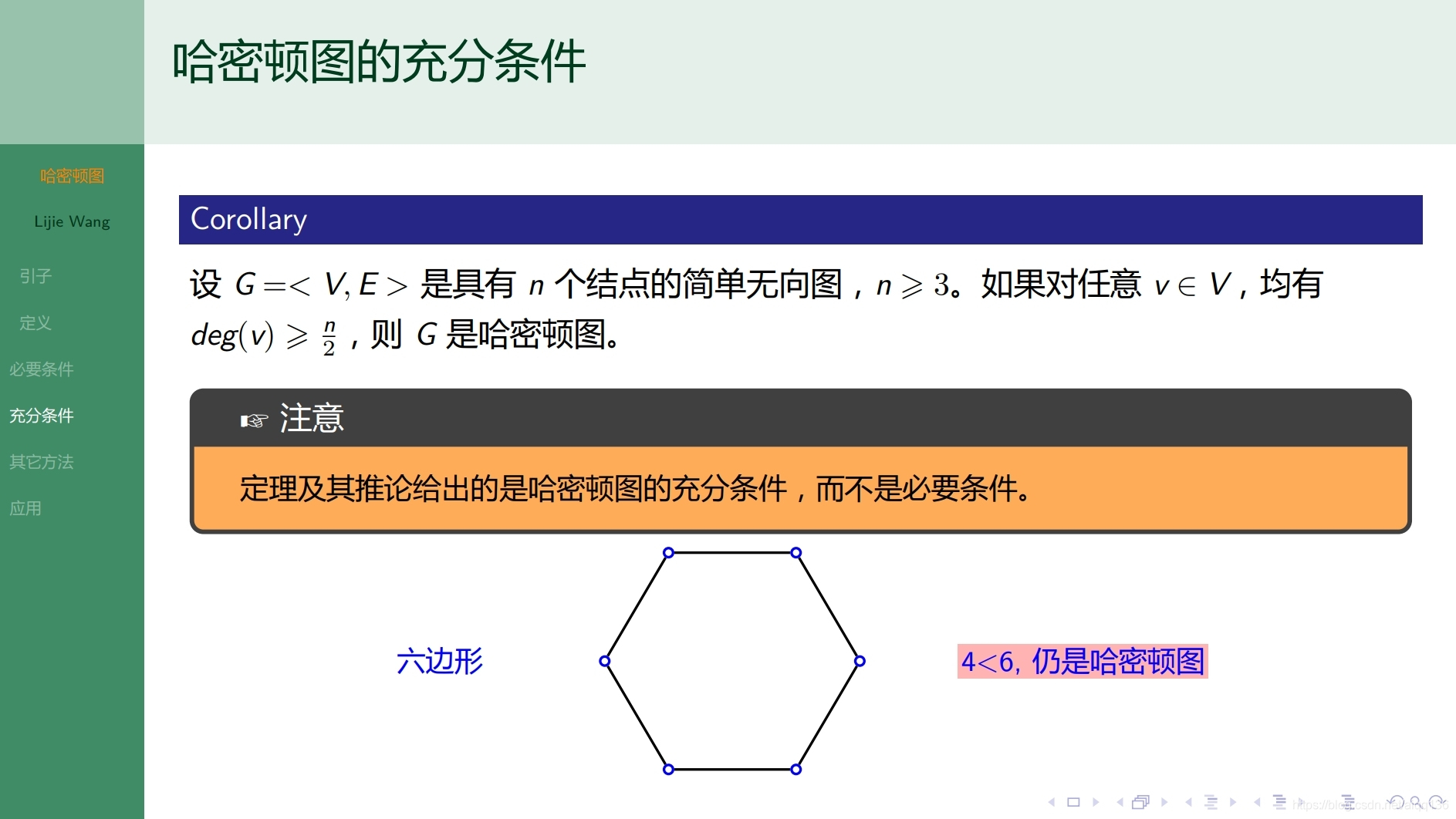
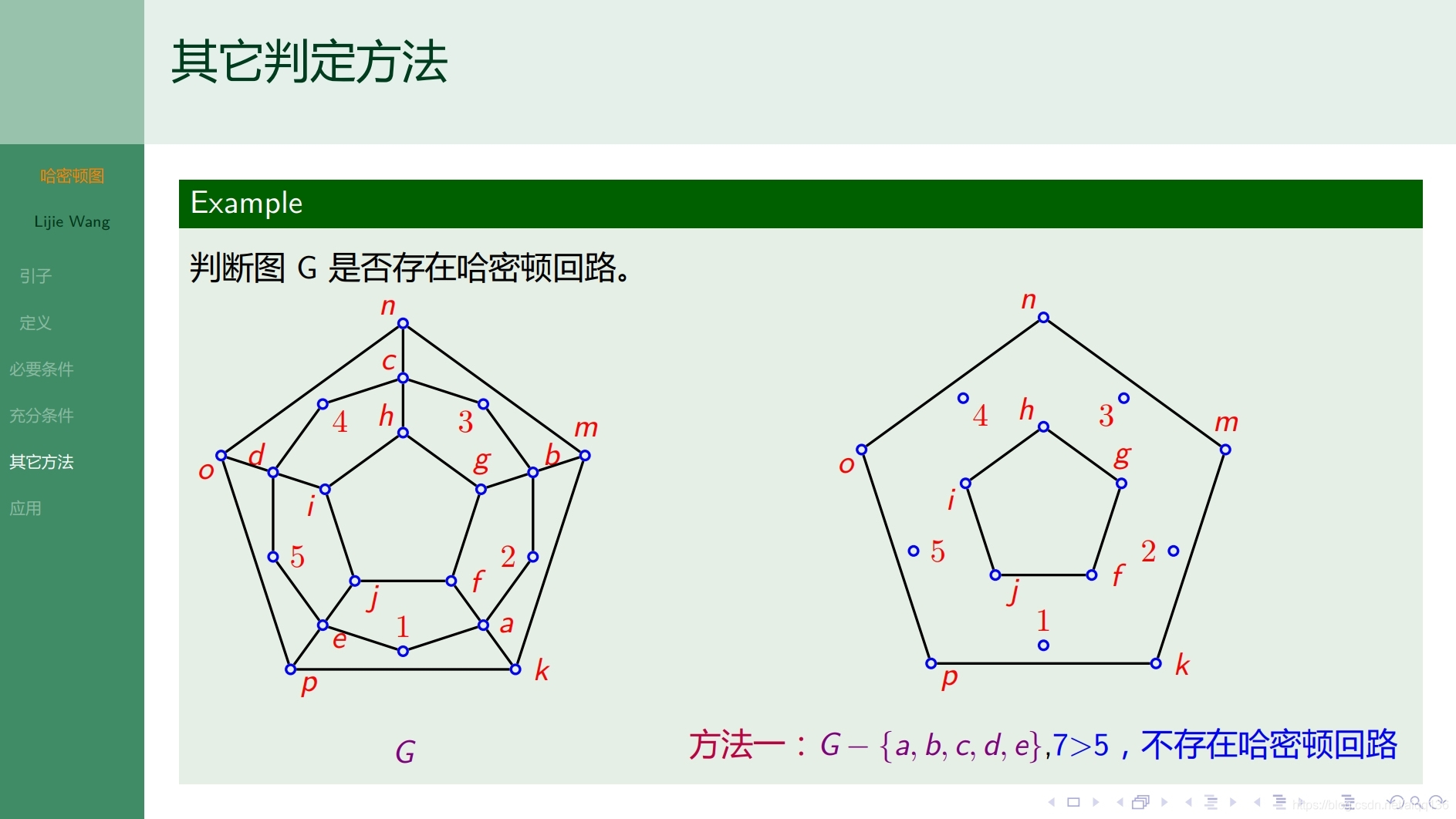
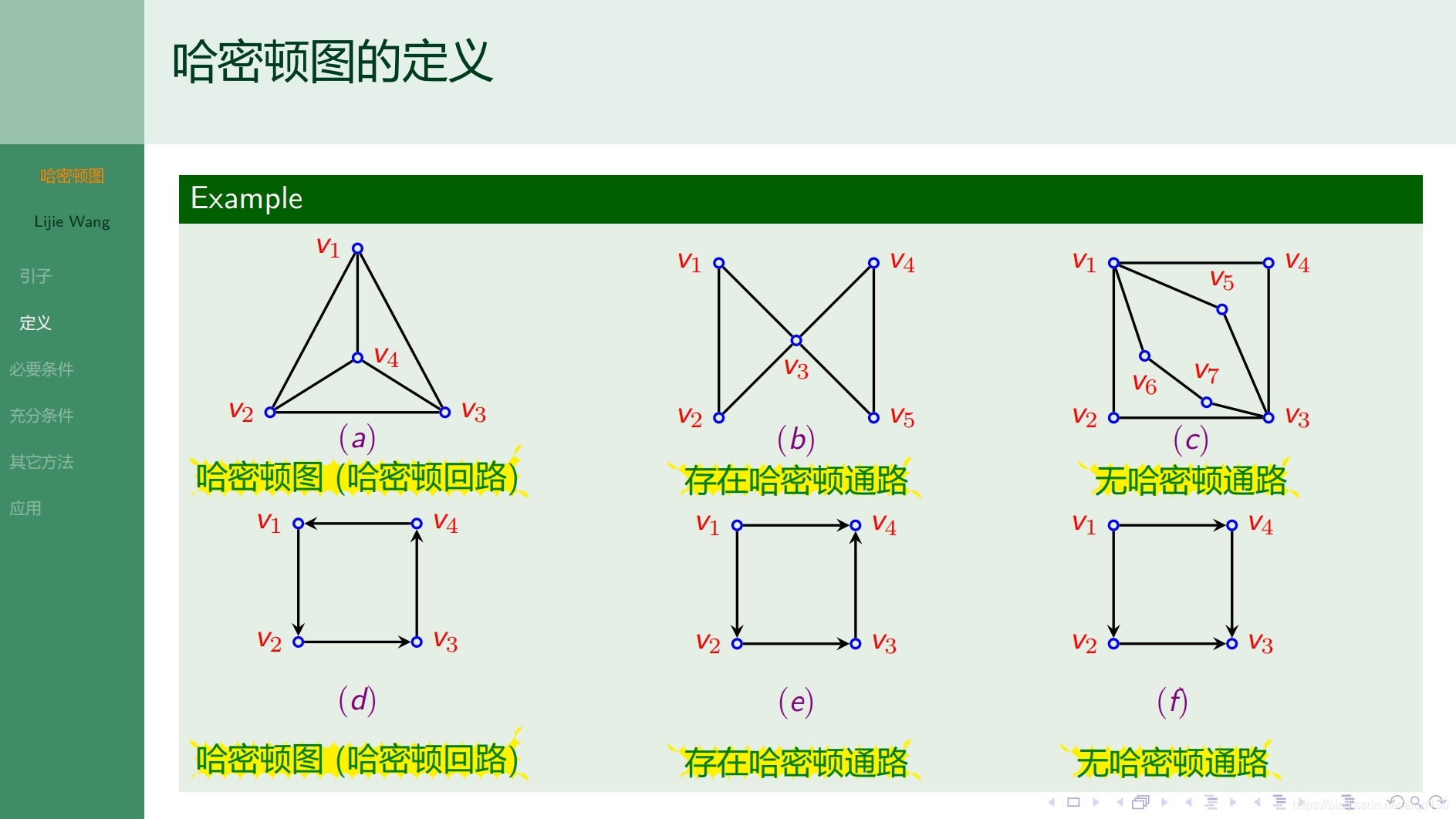
10.2.1特殊图 哈密顿图

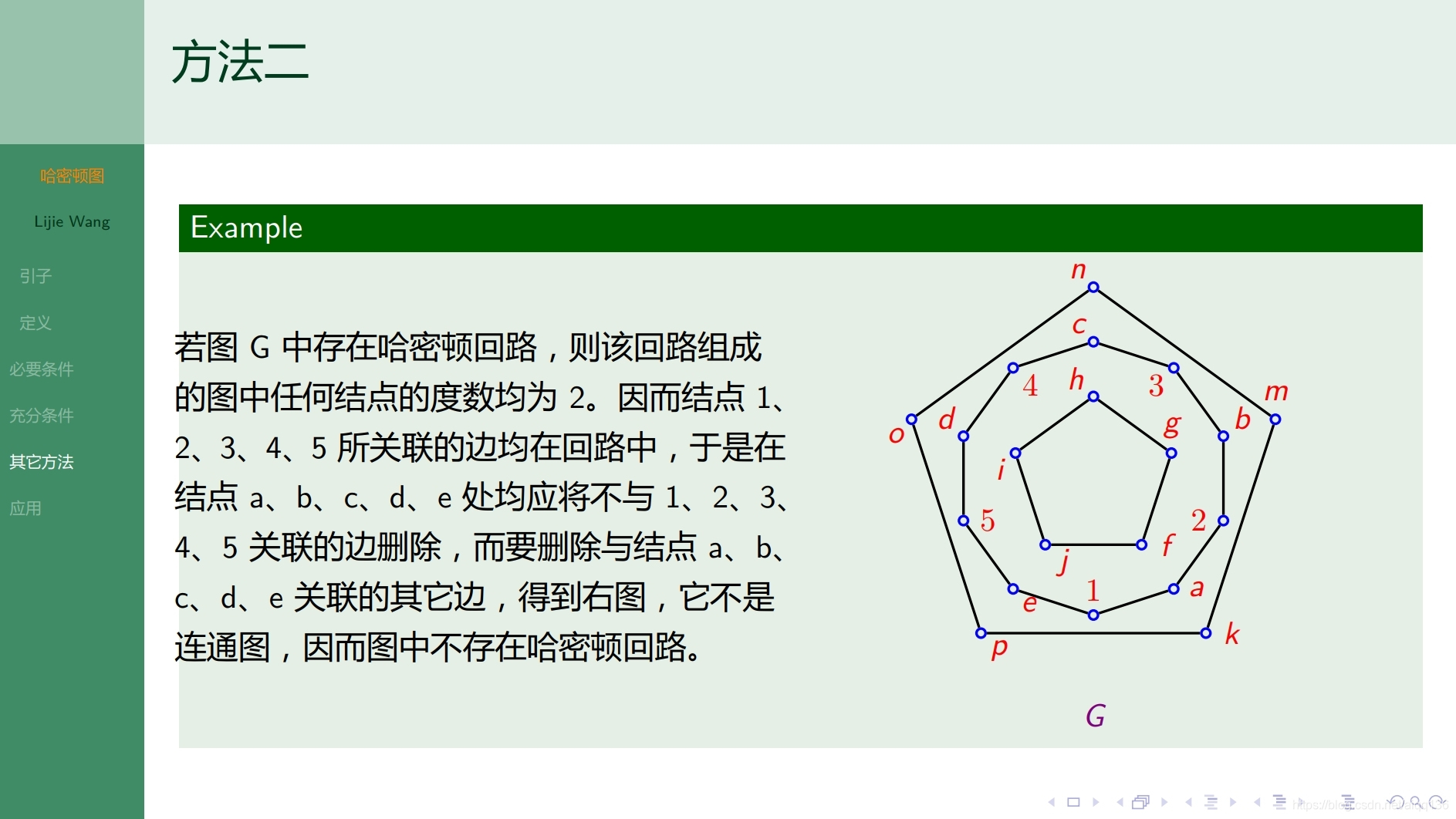
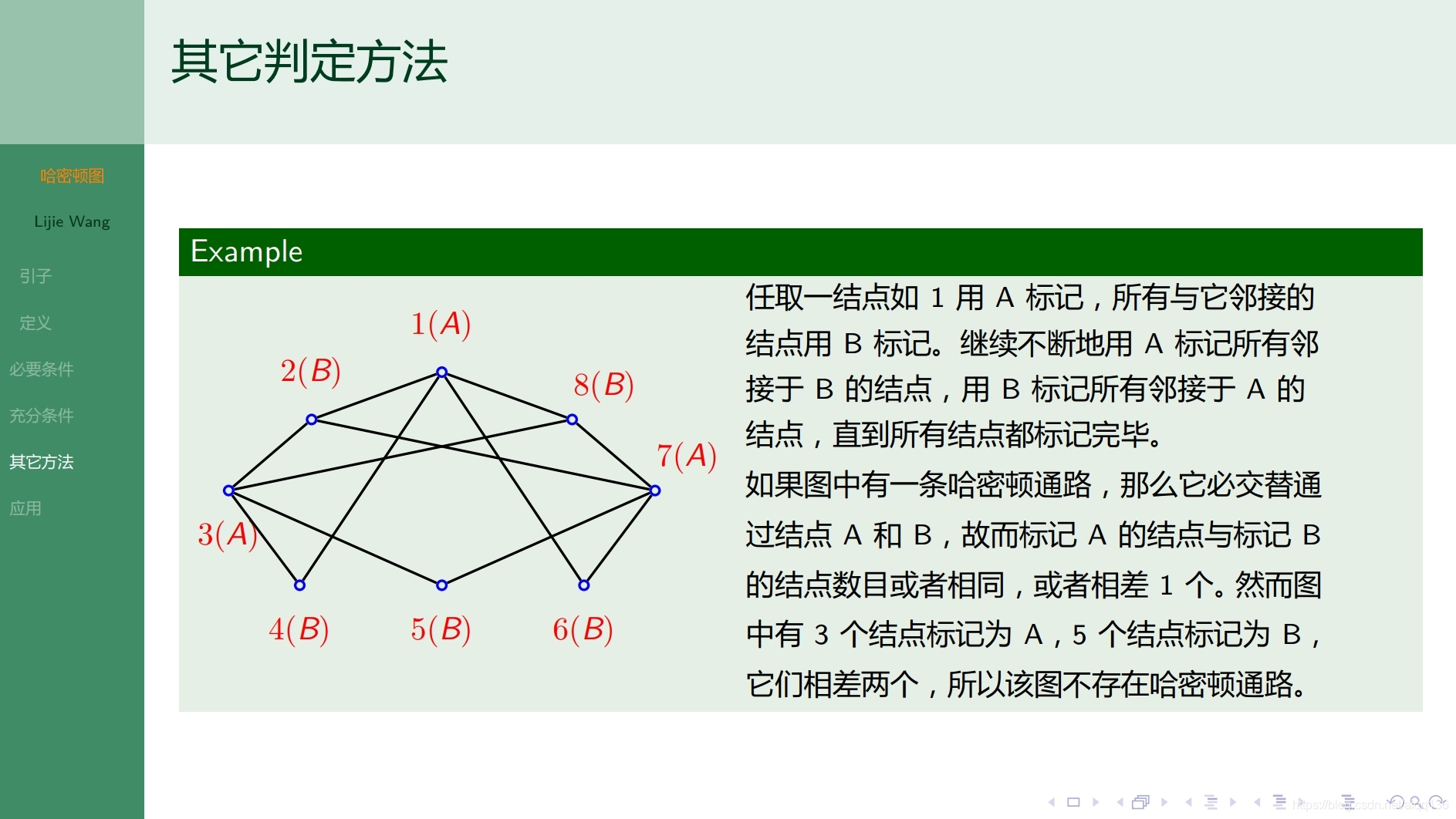
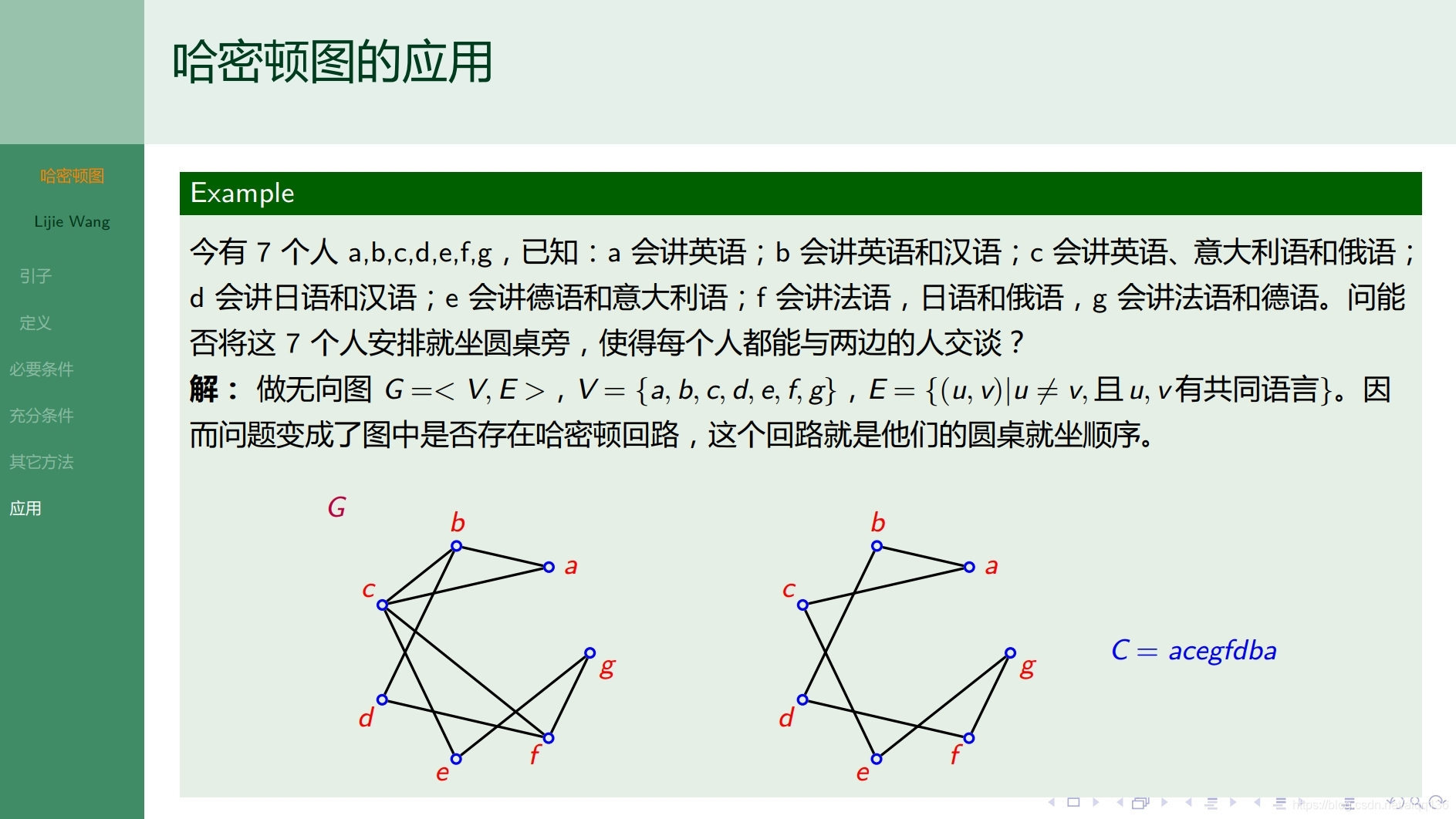
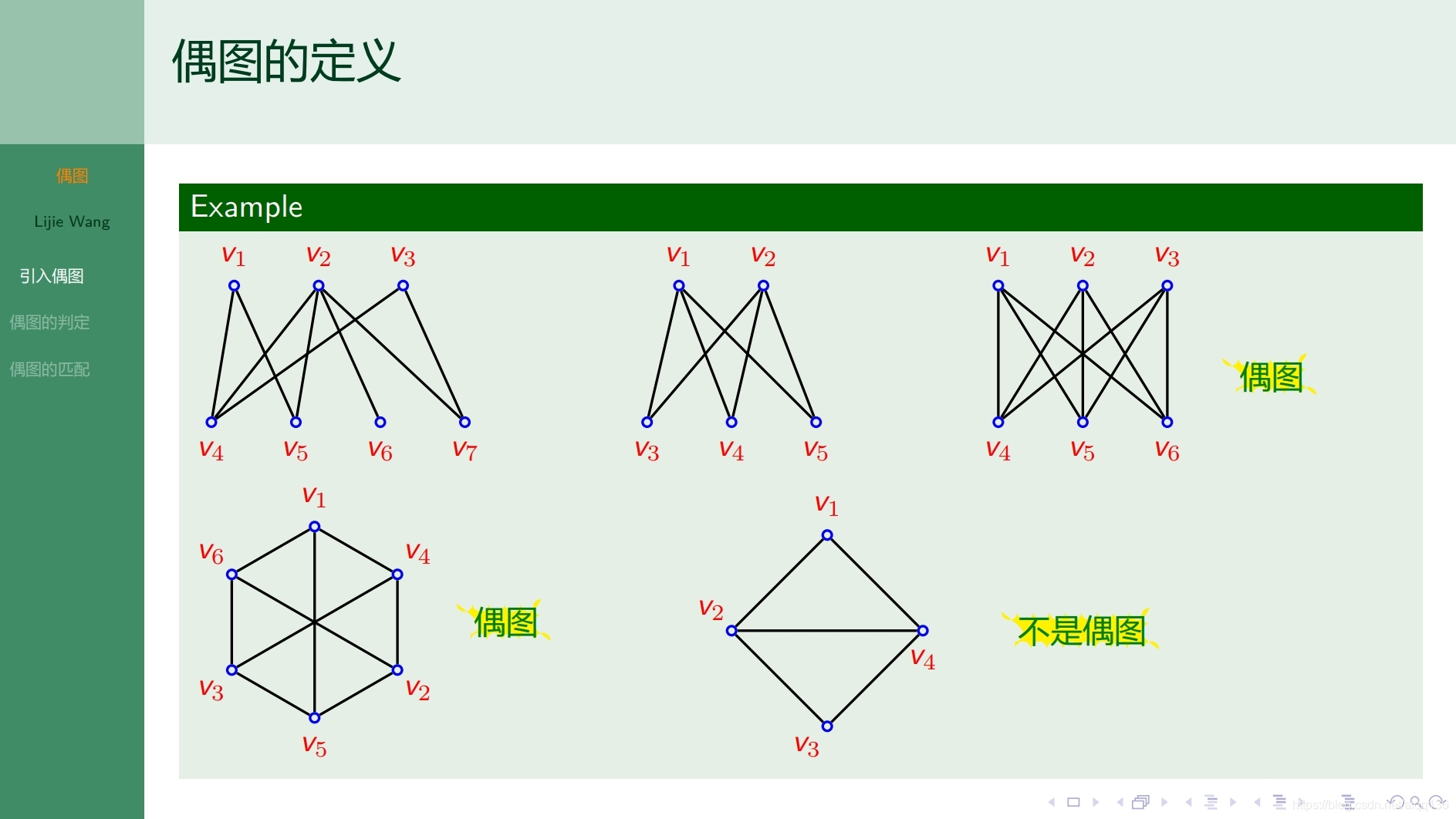
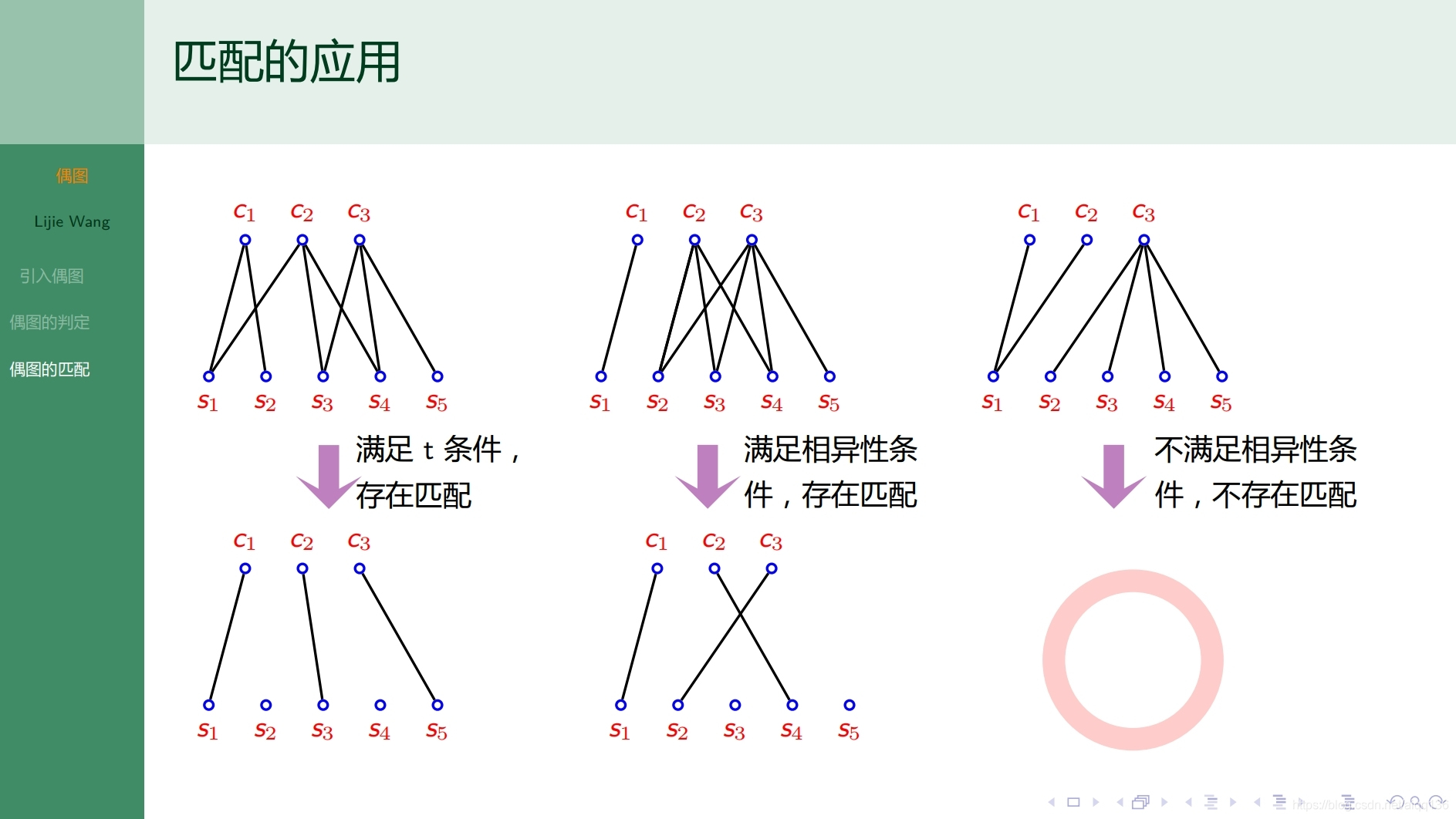
10.3.1特殊图 偶图

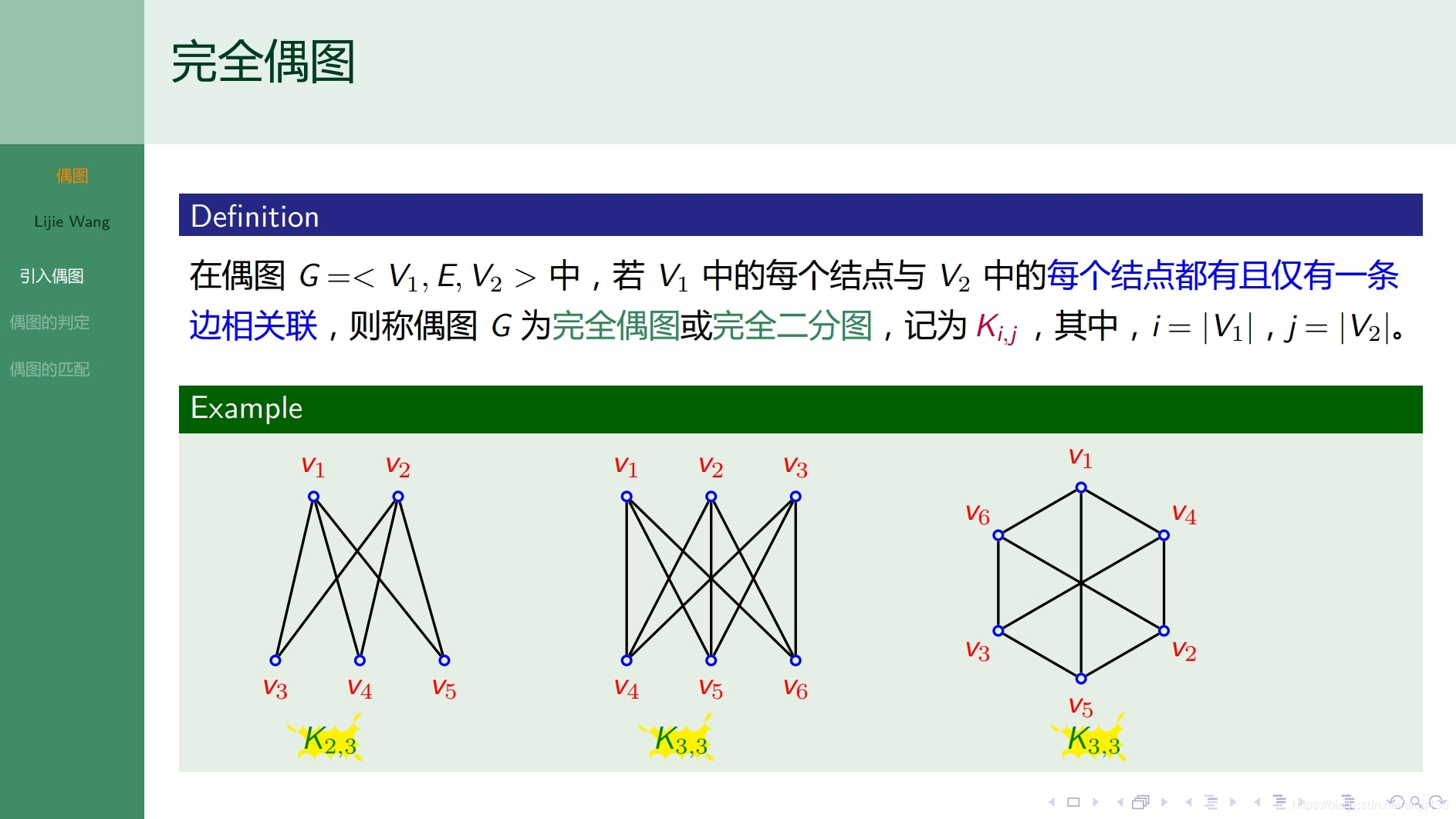
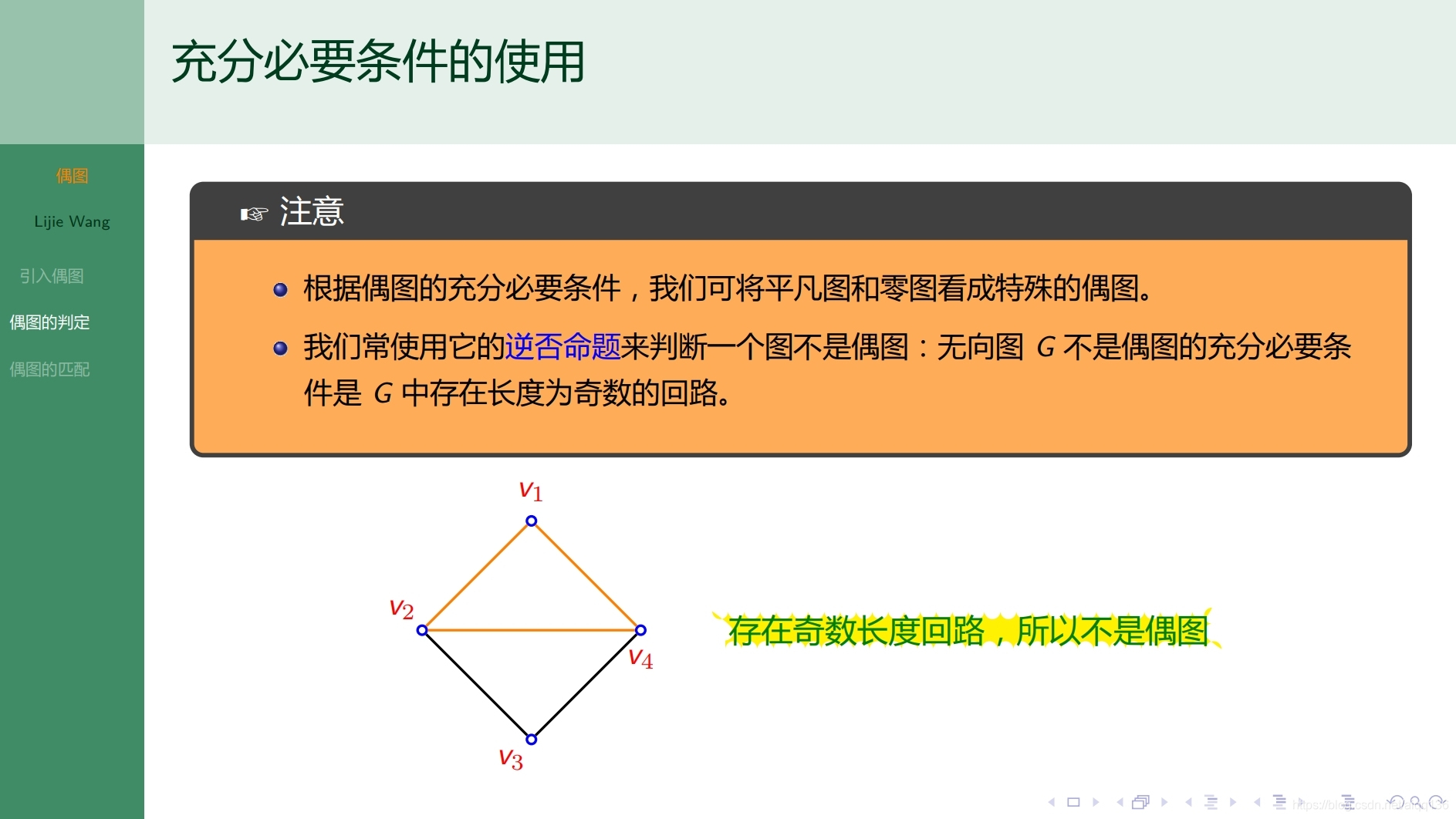
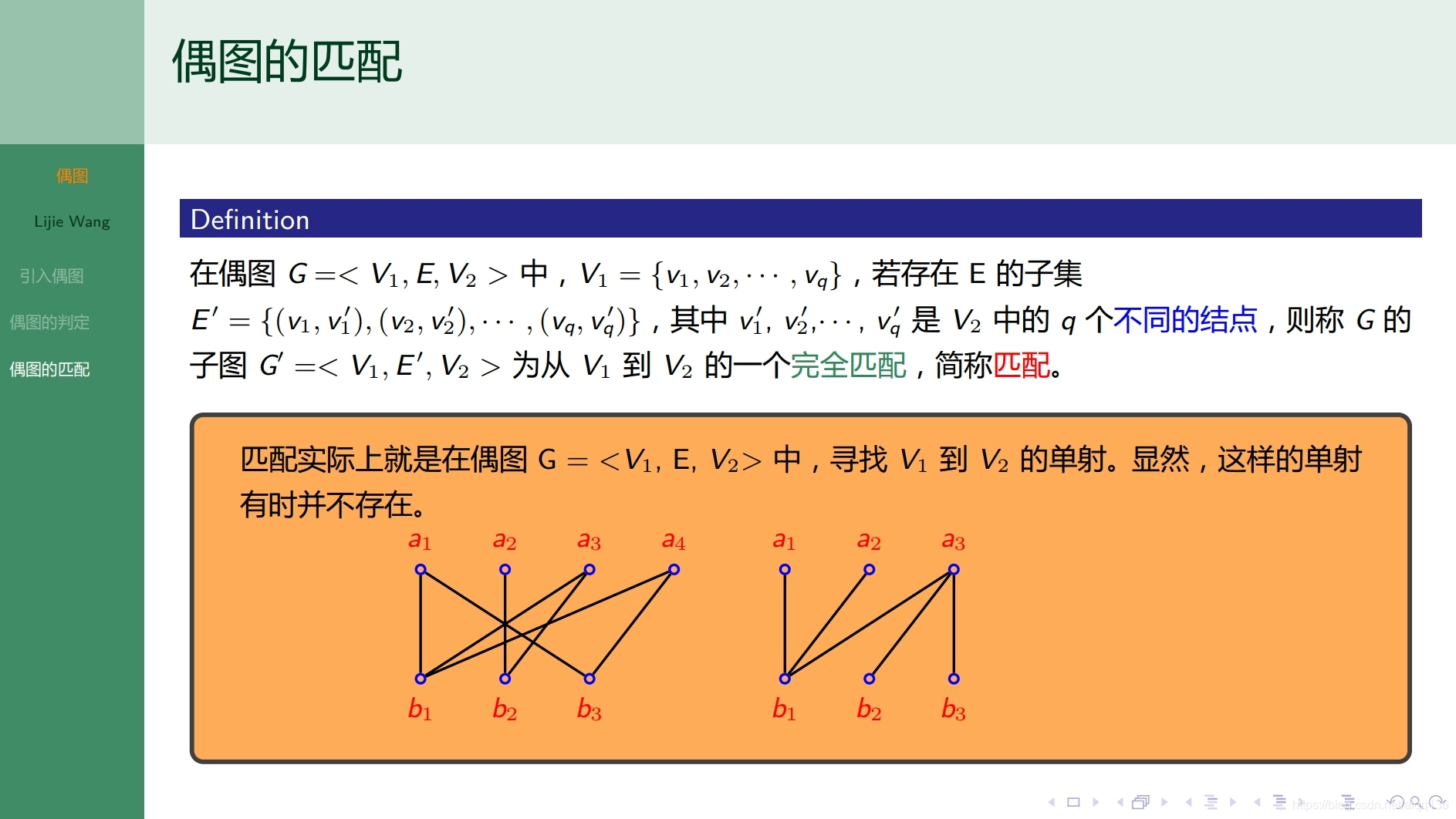
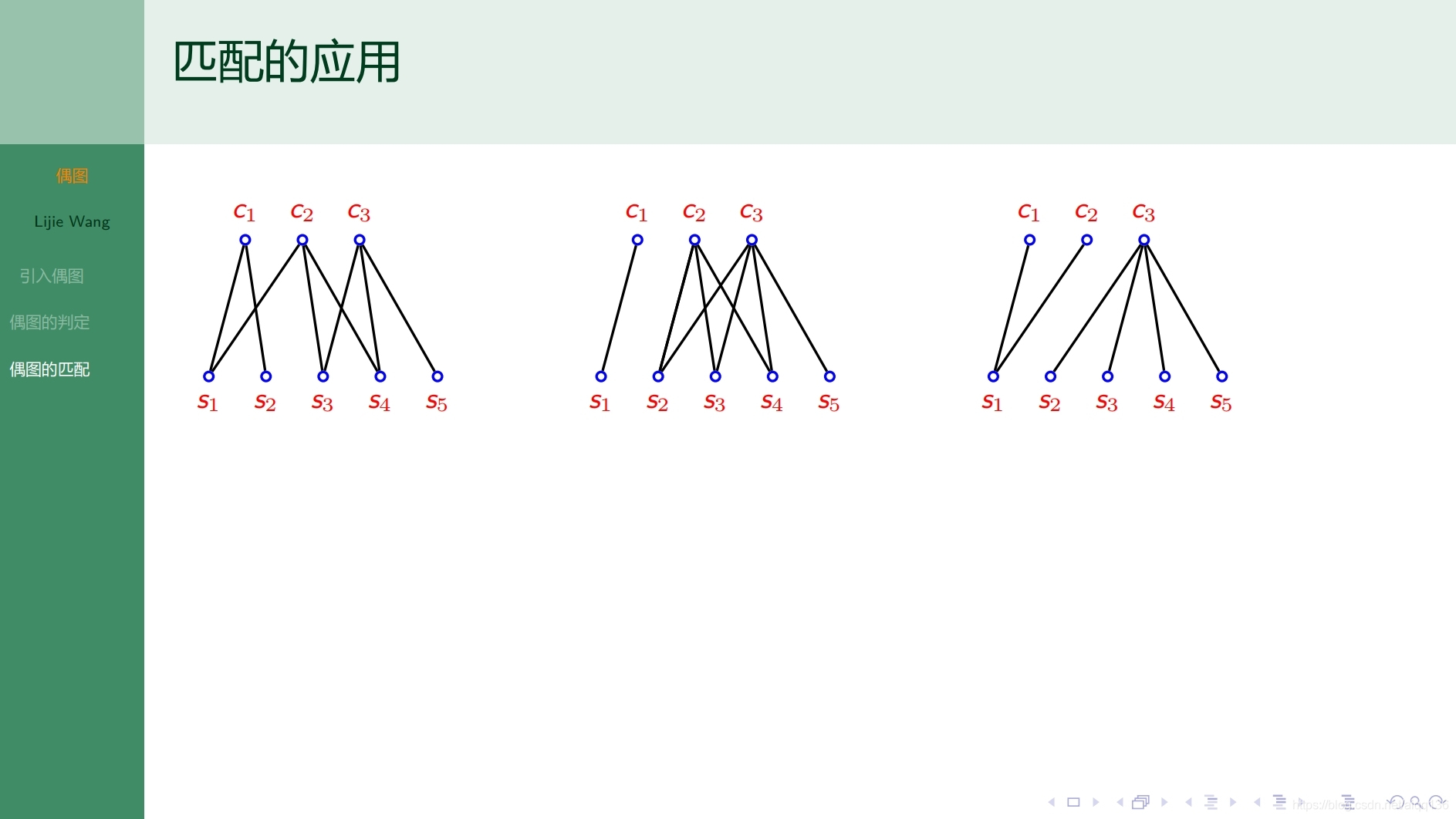
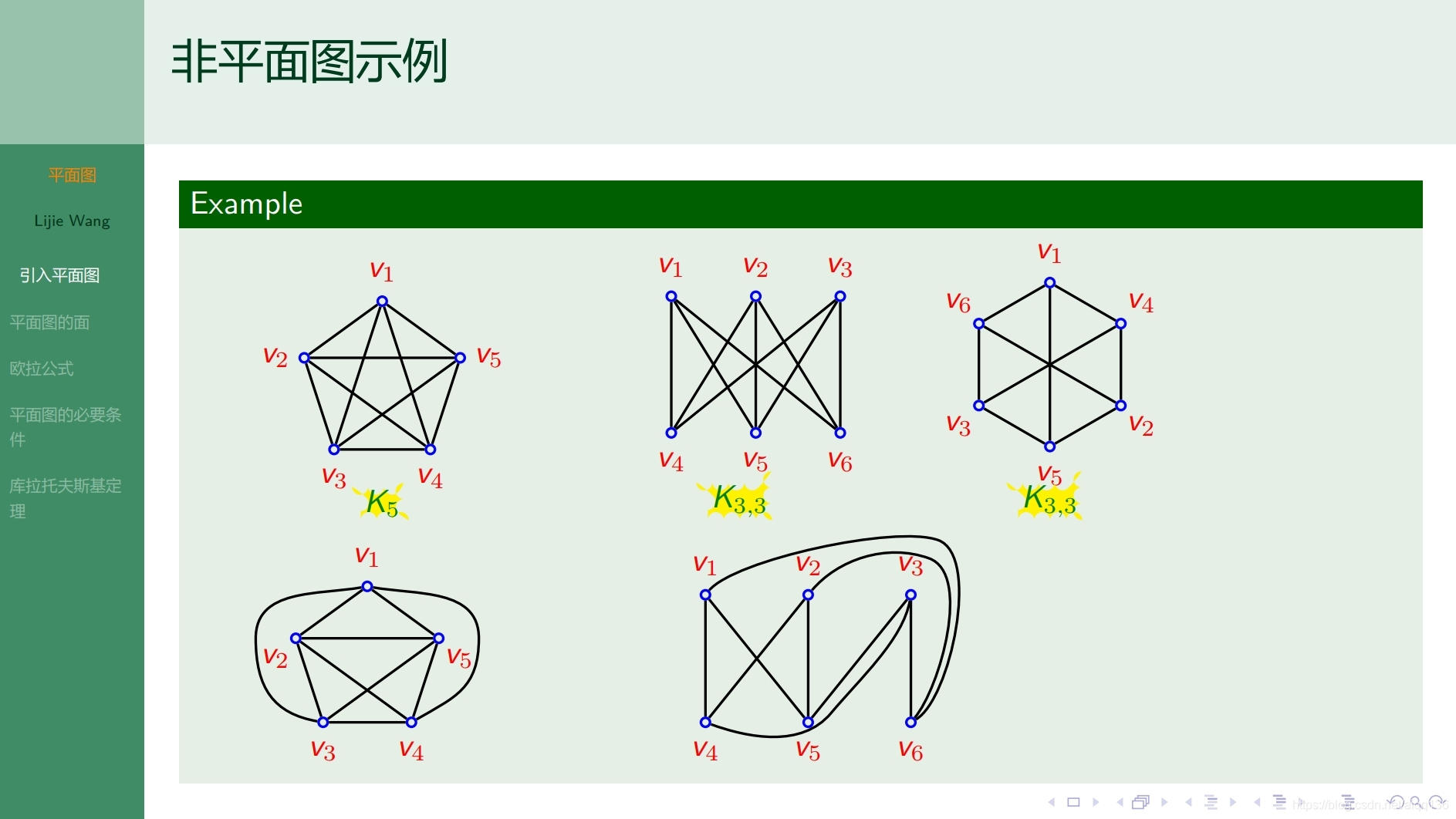
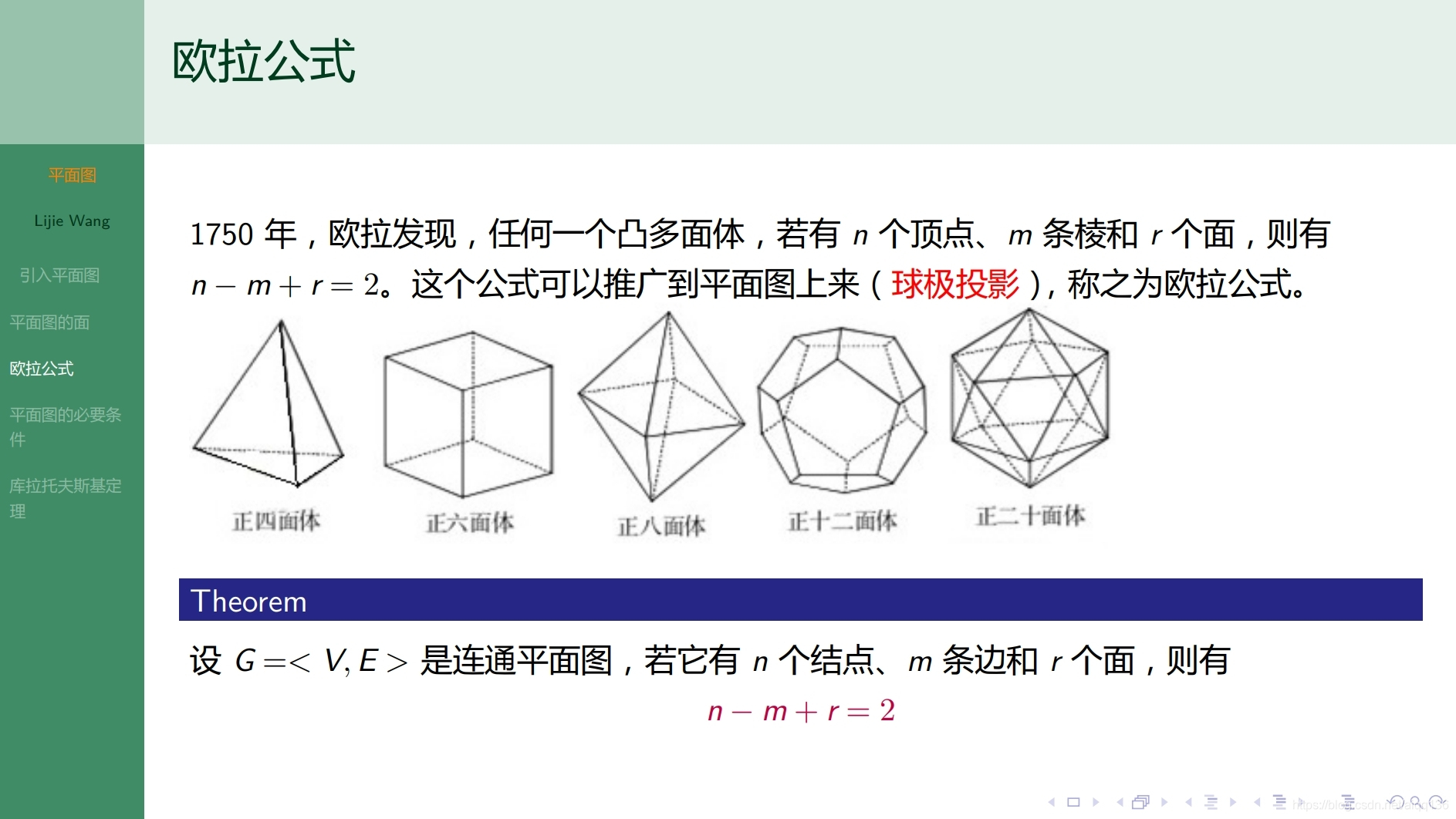
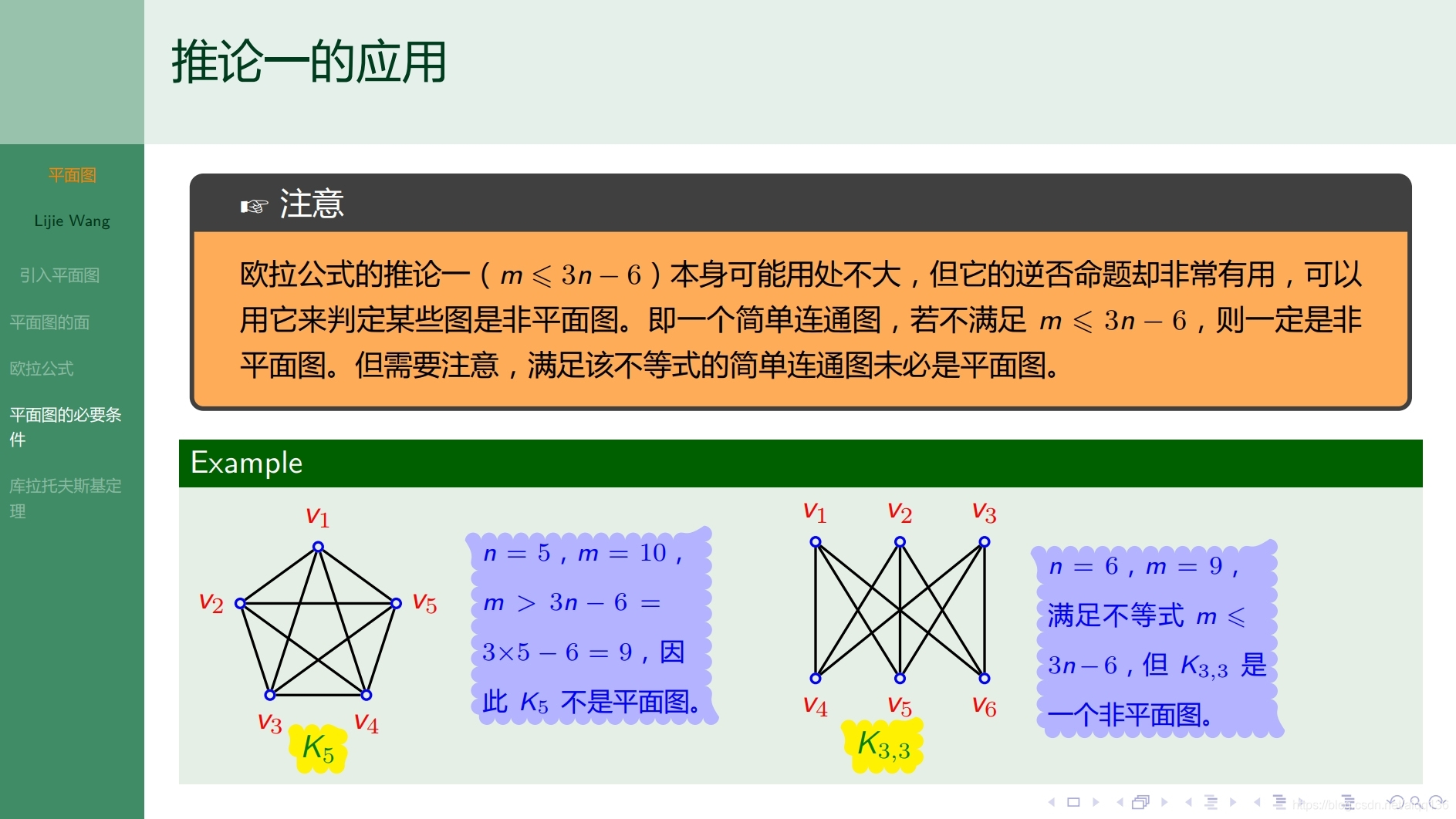
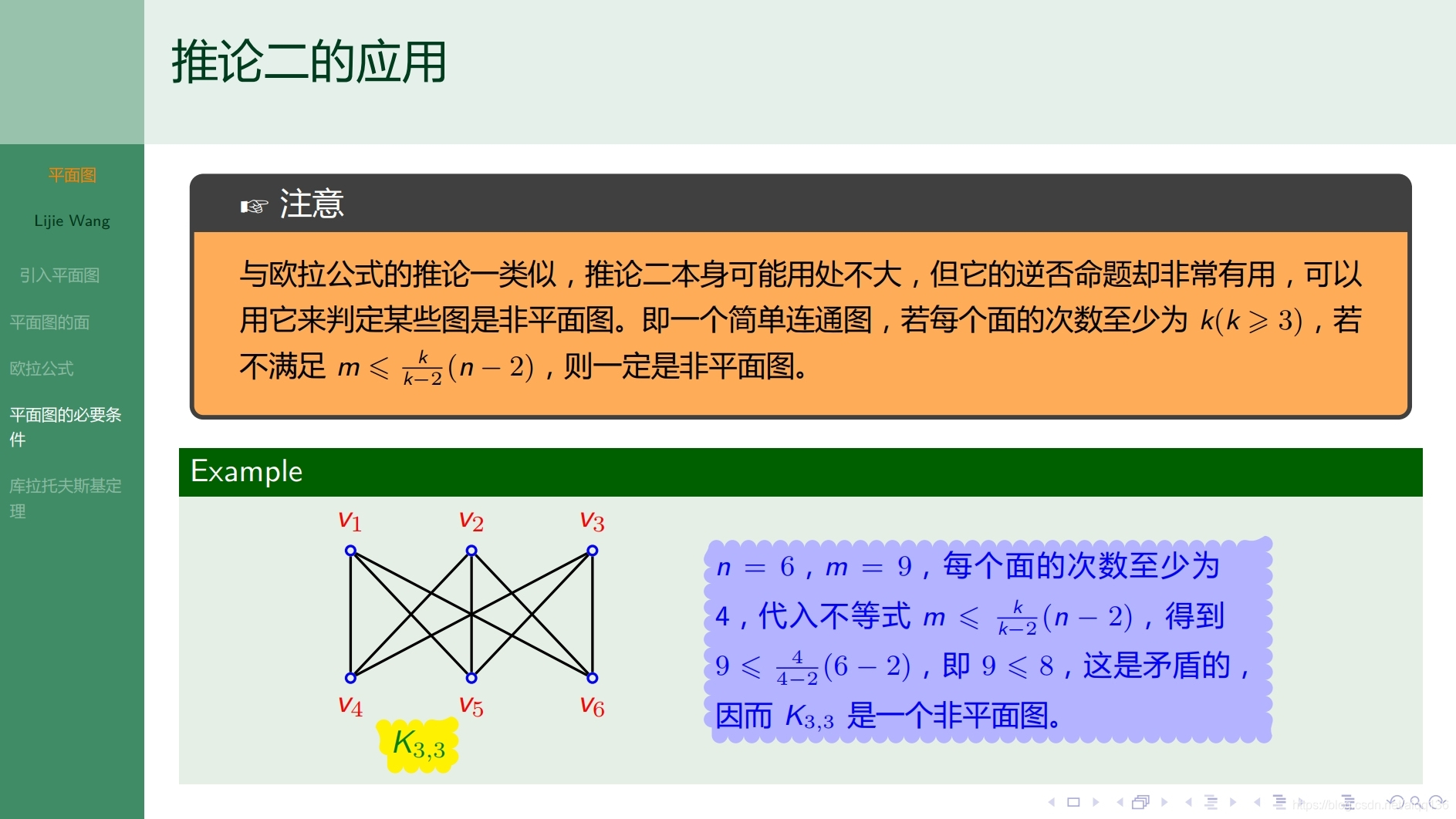
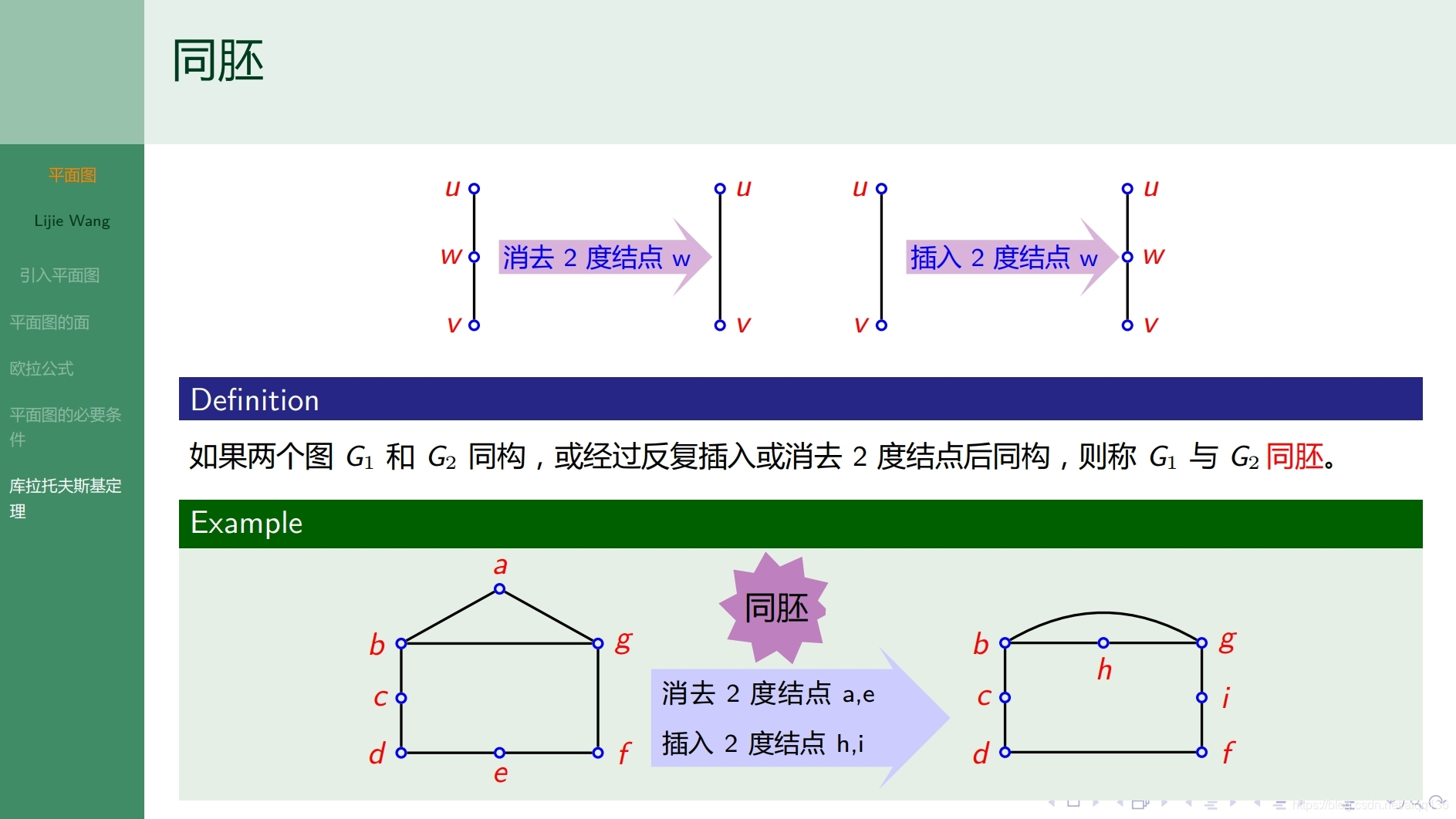
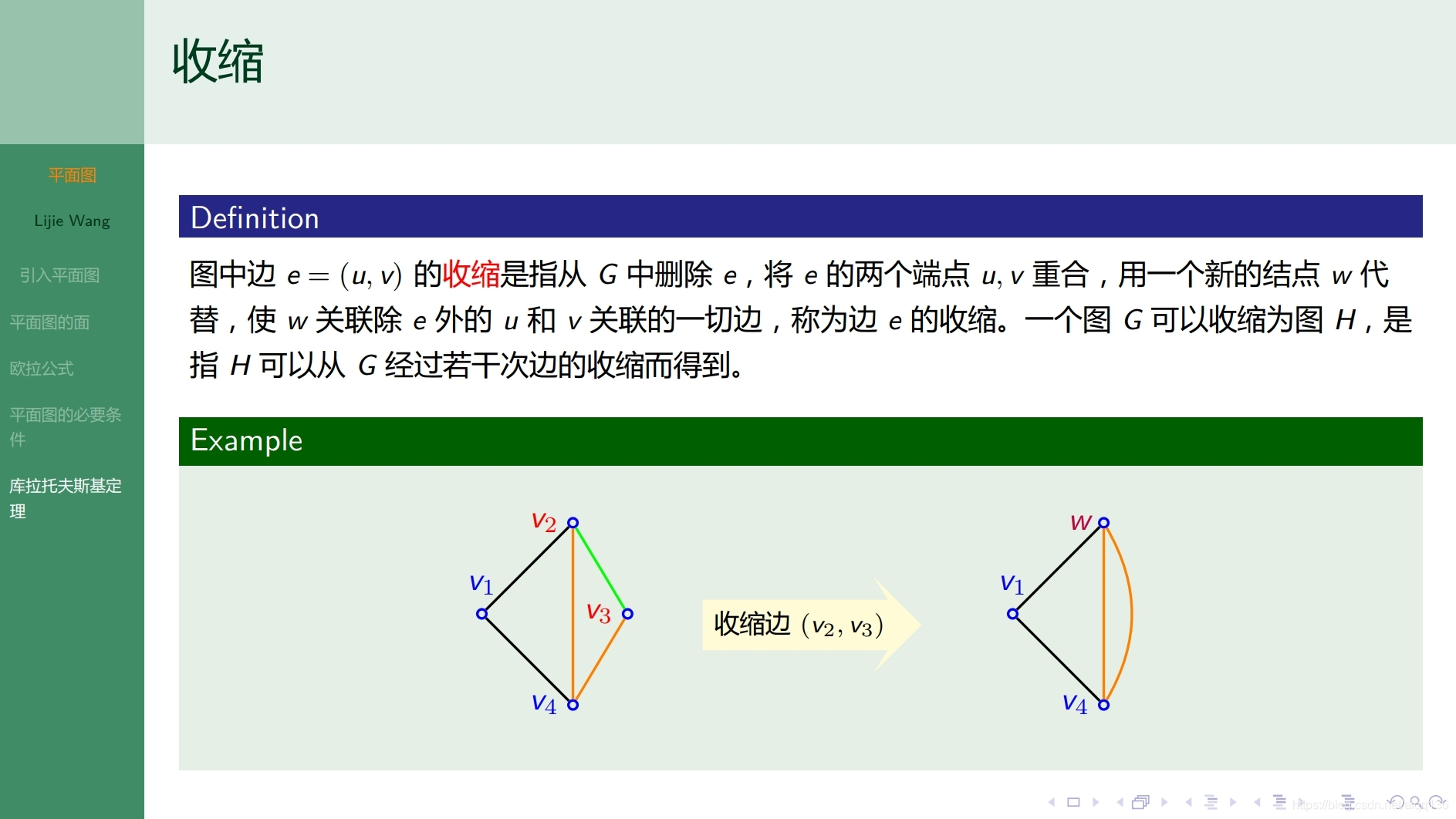
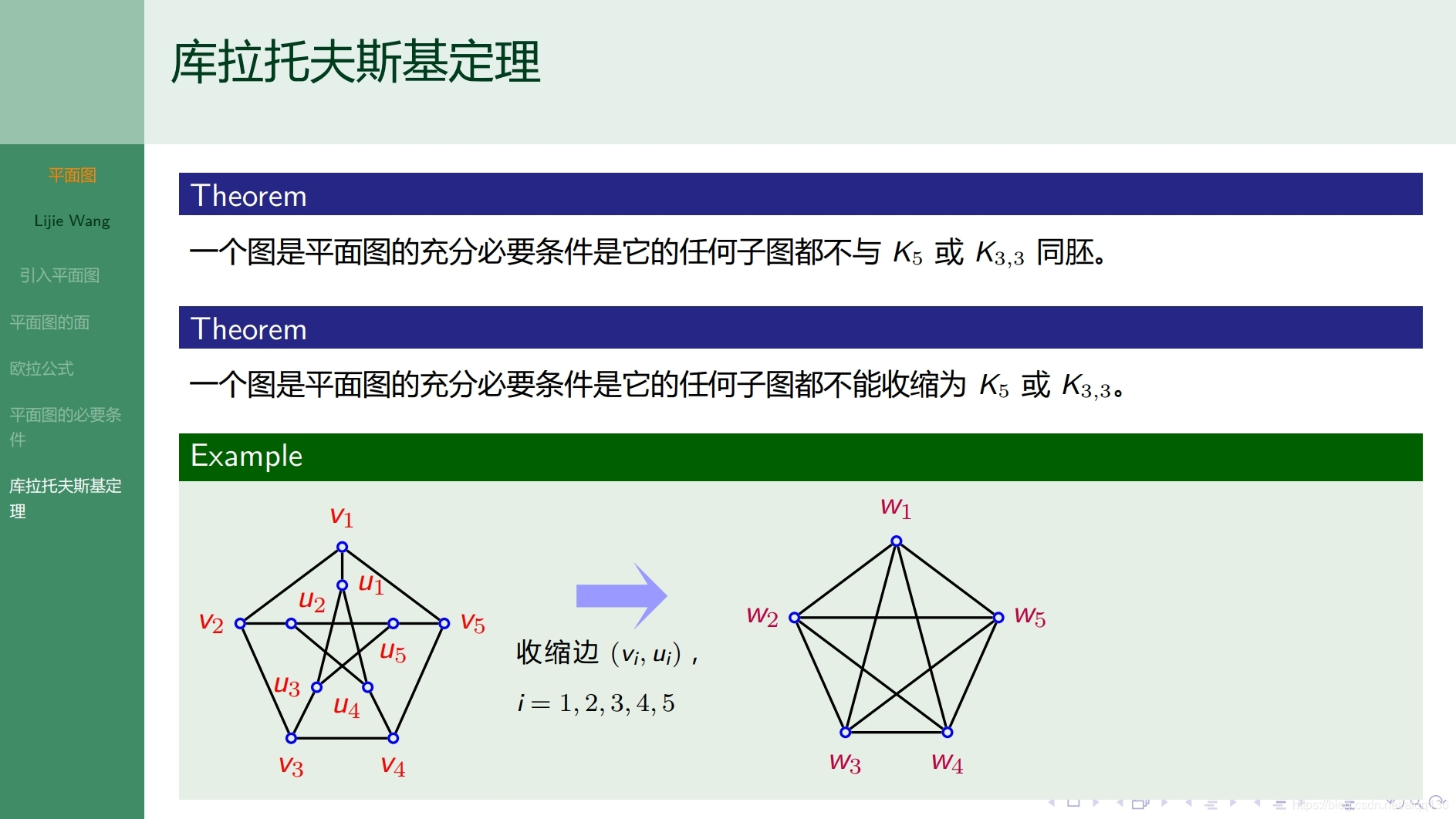
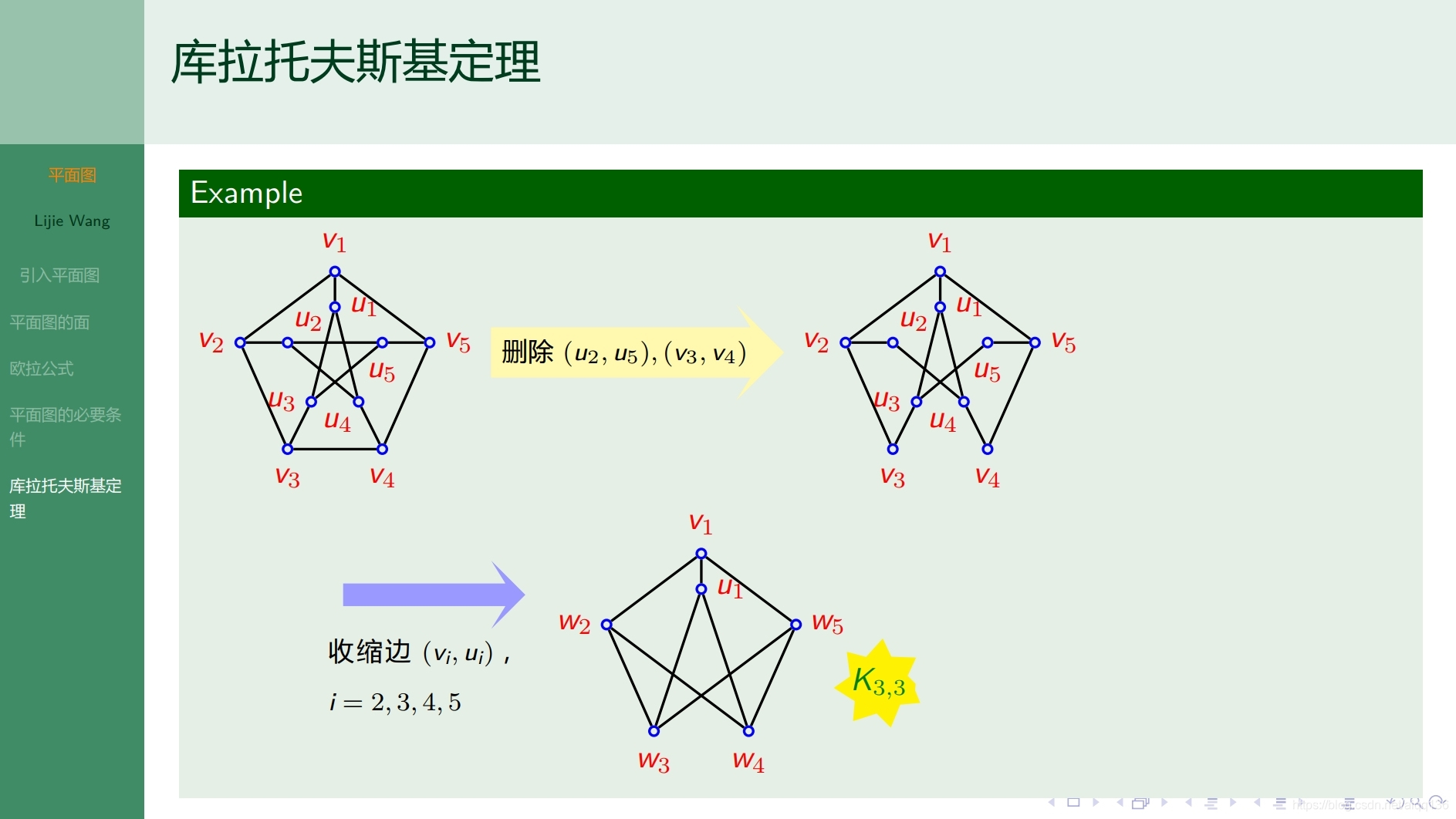
10.4.1特殊图 平面图