Constrained Delaunay Triangulation定义的理解

• Delaunay Triangulation 定义：

  Let S be a set of points in the plane. A triangulation T is a Delaunay triangulation of S if for each edge e of T there exists a circle c with the following properties:
  (1) The endpoints of edge e are on the boundary of c.
  (2) No other vertex of S is in the interior of c.
  If no four points of S are cocircular then the Delaunay triangulation is unique.

  大白话： 设S为源点集，若一个三角剖分T满足以下条件，则称其为点集S的一个Delaunay三角剖分：对T中的每一条边e，都存在一个圆c，1-边e的两个端点都在圆c上(感觉这个地方有问题，应该是对于T中的每一个三角形，其外接圆内不包含任何其他顶点)，2-并且S中所有其他的顶点都不在圆内(可以在圆上或者在圆外)。如果所有顶点中，没有四个或四个以上来自S的顶点在这样的伴生圆上，那么这个Delaunay剖分是唯一的。

• Constrained Delaunay Triangulation 定义：

  Let G be a straight-line planar graph. A triangulation T is a constrained Delaunay triangulation (CDT) of G if each edge of G is an edge of T and for each remaining edge e of T there exists a circle c with the following properties:
  (1) The endpoints of edge e are on the boundary of c.
  (2) If any vertex v of G is in the interior of c then it cannot be “seen” from at least one of the endpoints of e (i.e., if you draw the line segments from v to each endpoint of e then at least one of the line segments crosses an edge of G).

  大白话： 若三角剖分满足以下条件，则称其为约束性Delaunay三角剖分：若G中的每一条边(输入中的限制边)都在最后生成的三角剖分T的边中，并且所有新生成的边都满足1-新生成的边e的端点都在对应伴生圆上，2-若圆内有其他顶点(即除组成此三角外的其他顶点)，则此边e对圆内的顶点v是不可见的。
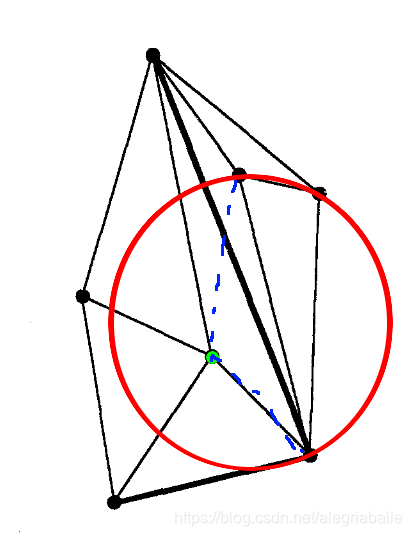
  我的理解： 如下图(图片来自下方论文，进行了修改)所示，若三角划分T中的一个三角形t，其外接圆中包含其他顶点(如图中绿点)，则t中的三条边对于此绿点来说都是不可见的(即t的任意边的两个端点与绿点连线必然会和其他边相交，如蓝色虚线所示，其与源输入的限制边相交，可以理解为图中的粗边挡住了绿点，使得三角形无法通过光线/直线看到绿点)，满足这样条件的三角剖分叫限制性Delaunay三角剖分。若T中所有的三角形t，其外接圆内都不存在其他的点，则这样的三角剖分就成为了Delaunay三角剖分。
  

• 定义来源 :
  L Paul Chew. 1987. Constrained delaunay triangulations. In Proceedings of the third
  annual symposium on Computational geometry. ACM, 215–222