Delaunay Triangulation-狄洛尼三角剖分

最新推荐文章于 2024-11-27 11:05:15 发布

AI剑客

最新推荐文章于 2024-11-27 11:05:15 发布

阅读量6.2k

点赞数 7

分类专栏： openCV AI 图像的处理

本文链接：https://blog.csdn.net/qq_43258953/article/details/105080150

版权

本文介绍了狄洛尼三角剖分的概念、特性及生成算法，包括Lawson算法和Bowyer-Watson算法。此外，还提及了与之相关的沃罗诺伊图，它在多个学科中有广泛应用。最后，提到了openCV库在实现这些算法上的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一，狄洛尼三角剖分
1.1 三角剖分（triangulation）
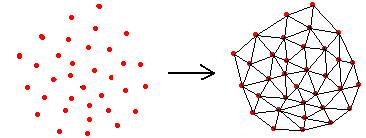
给定平面上的一组点，将平面细分成以这些点为顶点的三角形。
假设V是二维实数域上的有限点集，边e是由点集中的点作为端点构成的封闭线段，E为e的集合。那么该点集V的一个三角剖分T=(V,E)是一个平面图G，该平面图满足条件：
（1）除了端点，平面图中的边不包含点集中的任何点。
（2）没有相交边。
（3）平面图中所有的面都是三角面，且所有三角面的合集是散点集V的凸包。
在这里插入图片描述
1.2 狄洛尼三角剖分（Delaunay Triangulation）
狄洛尼三角剖分准则
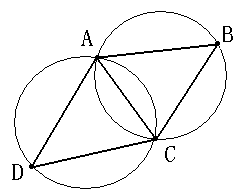
1）空圆特性：狄洛尼三角网是唯一的（任意四点不能共圆），在狄洛尼三角形网中任一三角形的外接圆范围内不会有其它点存在。

2）最大化最小角特性
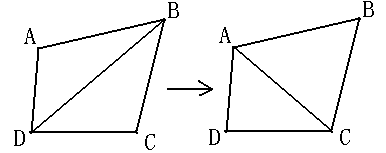
在散点集可能形成的三角剖分中，狄洛尼三角剖分所形成的三角形的最小角最大。从这个意义上讲，狄洛尼三角网是“最接近于规则化的”三角网（在两个相邻的三角形构成凸四边形的对角线，在相互交换后，两个内角的最小角不再增大）。
在这里插入图片描述
3）狄洛尼三角剖分特性
（1）最接近：以最接近的三点形成三角形，且各线段（三角行的边）皆不相交。
（2）唯一性：不论从区域何处开始构建，最终都将得到一致的结果。
（3）最优性：任意两个相邻三角形构成的凸四边形的对角线如何可以互换的话，那么两个三角形六个内角中最小角度不会变化。
（4）最规则：如果将三角网中的每个三角形的最小角进行升序排列，则狄洛尼三角网的排列得到的数值最大。
（5）区域性：新增、删除、移动某一个顶点只会影响邻近的三角形。
（6）具有凸边形的外壳：三角网最外层的边界形成一个凸多边形的外壳。

4)生成狄洛尼三角剖分的算法
Lawson算法:
逐点插入Lawson算法是Lawson在1977年提出的。该算法思路简单，易于编程实现。
（1）建立一个大的三角形或多边形，把所有数据点包围起来；
（2）向其中插入一点，该点与包含它的三角形三个顶点相连，形成三个新的三角形；
（3）逐个对它们进行空外接圆检测，同时用LOP进行优化，即通过交换对角线的方法来保证所形成的三角网为狄洛尼三角网。
Bowyer-Watson算法:
目前广泛采用的生成狄洛尼三角剖分的算法是Bowyer-Watson算法，这是一种逐点插入方式生成狄洛尼三角网的算法，主要步骤如下：
（1）建立初始三角网格：针对给定的点集V，找到一个包含该点集的矩形R，称R为辅助窗口。连接R的任意一条对角线，形成两个三角形，作为初始狄洛尼三角网格。
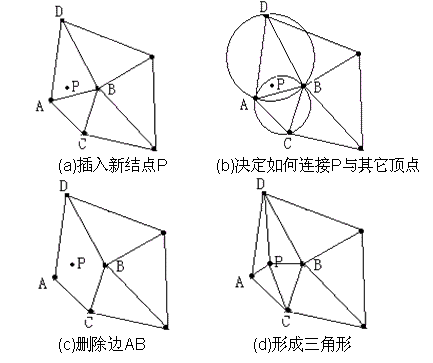
（2）逐点插入：假设已经有一个狄洛尼三角网格TT TT，在其内部再插入一个点P，找到点P所在三角形。从P所在的三角形开始，搜索该三角形的邻近三角形，并进行空外接圆检测。找到外接圆包含点P的所有的三角形并删除这些三角形，形成一个包含P的多边形空腔，称之为狄洛尼空腔。然后连接P与狄洛尼腔的每一个顶点，形成新的狄洛尼三角网格。
（3）删除辅助窗口R：重复（2），当点集V中所有点都已经插入到三角形网格中后，将顶点包含辅助窗口R的三角形全部删除。
在这里插入图片描述

1.3 沃罗诺伊图
沃罗诺伊图（Voronoi Diagram，也称作Dirichlet tessellation，狄利克雷镶嵌）由俄国数学家格奥尔吉·沃罗诺伊建立的空间分割算法。灵感来源于笛卡尔用凸域分割空间的思想。在几何，晶体学建筑学，地理学，气象学，信息系统等许多领域有广泛的应用。
对三角剖分中的所有三角形各边做垂直平分线，将各相邻三角形三边的垂直平分线的交点（即外接圆圆心）连接起来得到一个多边形，称这个多边形为沃罗诺伊图。
在这里插入图片描述

二，openCV的代码实现

# !/usr/bin/python

import cv2
import numpy as np
import random
import dlib  # 人脸识别的库 dlib


# Check if a point is inside a rectangle
def rect_contains(rect, point):
    if point[0] < rect[0]:
        return False
    elif point[1] < rect[1]:
        return False
    elif point[0] > rect[2]:
        return False
    elif point[1] > rect[3]:
        return False
    return True


# Draw a point
def draw_point(img, p, color):
    cv2.circle(img, p, 2, color, -1, cv2.LINE_AA, 0)


# Draw delaunay triangles
def draw_delaunay(img, subdiv, delaunay_color):
    triangleList = subdiv

最低0.47元/天解锁文章