（一）常见的回归评价指标及代码实现与应用

每个机器学习模型都试图使用不同的数据集来解决具有不同目标的问题，因此，对于不同的机器学习任务，在充分理解上下文的基础上，选择合适的机器学习评价指标是非常重要的。只有了解了本次机器学习建立模型的任务，才能选择合适的评价指标。

本篇博客关注回归问题的评价指标。先介绍常用的评价指标，然后用代码实现所述评价指标。

分类问题的评价指标的问题随后会整理。

一、回归指标（Regression Metrics）

1.1 均方误差 MSE

MSE （Mean Squared Error）称为均方误差，又被称为 L2范数损失 。公式如下：

意义很明确，用 真实值-预测值 然后平方之后求和平均。

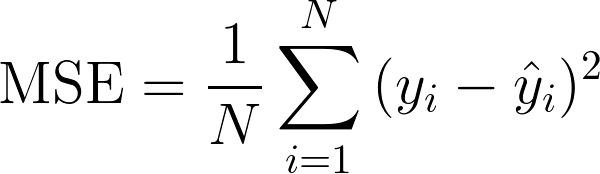
1.2 均方根误差 RMSE

RMSE（Root Mean Squard Error）称为均方根误差。公式如下：

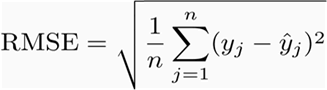
可以看到，MSE开根号后就成了RMSE。

为什么要开根号呢？有意义么？其实实质是一样的。只不过用于数据更好的描述。

例如：要做房价预测，每平方是万元，我们预测结果也是万元。那么差值的平方单位即是千万级别的。那我们就不太好描述自己做的模型效果。于是开根号后，误差结果的量纲就跟原始数据的是一个级别了，更便于描述我们预测的结果。

1.3 平均绝对误差 MAE

平均绝对误差MAE（Mean Absolute Error）又被称为 L1范数损失。公式如下：

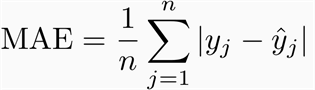
意义很明确，MAE是预测值与观测值之间的绝对差值的平均值。

---

RMSE(MSE)和MAE都是最常用的回归评价指标，那么我们应该如何选择呢？

MAE直接取平均偏移，而RMSE比MAE惩罚更高的差异。比如：

案例1：实际值= [2,4,6,8]，预测值= [4,6,8,10]
案例2：实际值= [2,4,6,8]，预测值= [4,6,8,12]

这时，

案例1的MAE = 2.0，案例1的RMSE = 2.0；
案例2的MAE = 2.5，案例2的RMSE = 2.65

从上面的例子中，我们可以看到，对于预测较差的值，RMSE比MAE给与更高的惩罚。通常，RMSE将高于或等于MAE。它等于MAE的情况是当所有差异相等或为零时。

然而，RMSE是许多模型的默认评价指标，因为根据RMSE定义，其是平滑可微的，从而使得更容易执行数学运算，例如求梯度。

还有一个重要的区别是，最小化一组数字上的平方误差RMSE会导致找到它的均值，并且最小化平均绝对误差MAE会导致找到它的中位数。这就是为什么MAE对异常值具有鲁棒性而RMSE不强的原因。

总结一下，RMSE与MAE的主要区别是：
①RMSE比MAE惩罚更高的差异
②RMSE是平滑可微的
③MAE对异常值更鲁棒

---

1.4 R Squared (R²) 和修正R²

1.4.1 R Squared (R²)

上面的几种衡量标准的取值大小与具体的应用场景有关系，很难定义统一的规则来衡量模型的好坏。比如说预测房价，那么误差单位就是万元，可能是3，4，5之类的结果。预测身高就可能是0.1，0.6之类的结果。分类算法的最经典的评价指标就是正确率，而正确率又在0～1之间，最高1，最低0。很直观，而且不同模型不同情景下都是一样的。那么回归有没有这样的衡量标准呢？答案是有的。

这就是我们要介绍的R²，它是一个无量纲化的指标。公式如下：

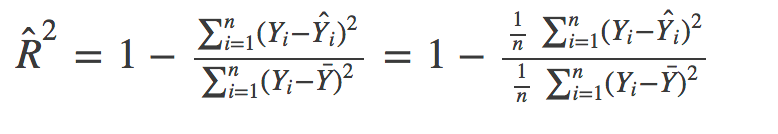
虽然看起来公式很复杂，但是仔细观察一下，发现很简单。

分子就是MSE。分母就是标签$Y$的方差。

我们可以把分母理解成，无论是什么数据，我们预测的结果就是$Y$的平均数。（瞎猜的误差）

那么：
如果结果是0，就说明我们的模型跟瞎猜差不多。
如果结果是1。就说明我们模型无错误。（分子是0，完全预测正确）
如果结果是0-1之间的数，就是我们模型的好坏程度。越大越好。
如果结果是负数。说明我们的模型还不如瞎猜，即还不如不训练模型，直接用均值作为我们预测的结果。

1.4.2 修正R²

R²用来评价模型的拟合程度。当我们在评价拟合程度的同时，也考虑到模型的复杂程度，那么修正R²(Adjusted R²)就被提出来。

修正R²是考虑到了自由度下的R².

$$R^2=1-\frac{S{S}_{\text{Res}}}{S{S}_{\text{Total}}}$$

考虑到残差的平方和$S{S}_{\text{Res}}$的自由度为$n-p-1$，总体平方和$S{S}_{\text{Total}}$的自由度为$n-1$，那么我们修正后的$R_{\text{Adj}}^2$的公式为
$$R_{\text{Adj}}^2=1-\frac{S{S}_{\text{Res}}/(n-p-1)}{S{S}_{\text{Total}}/(n-1)}=1-\frac{S{S}_{\text{Res}}}{S{S}_{\text{Total}}}\frac{(n-1)}{(n-p-1)}=1-(1-R^2)\frac{n-p-1}{n-1}$$

公式中$n$是样本的个数，$p$是变量的个数。

---

那么我们对于R²和修正R²，应该如何选择呢？

在前面我们也已经提到了，修正R²考虑到了模型的复杂程度。下面举例来说明：

如上图所示，case 1是有5个（x，y）观测值的简单情况。在case 2中，我们还有一个变量，它是变量1的两倍（与变量1完全相关）。在case 3中，我们对var2中产生了轻微干扰，使其不再与var1完全相关。

因此，如果我们为每种case拟合简单的线性回归模型，从逻辑上讲，相对于case 1，我们并没有向case 2和case 3提供额外或有用的信息。因此，我们的度量值不应该针对这些模型进行改进。然而，对于R²来说实际上并不是这样，它在模型2和3中值更高。但是如果我们使用修正R²就不会出现这个问题，它实际上在2和3的情况下都有所减少。

接下来，通过代码验证我们上面的说法：

import numpy as np
import pandas as pd
from sklearn import datasets, linear_model

def metrics(m,X,y):
    yhat = m.predict(X)
#    print(yhat)
    SS_Residual = sum((y-yhat)**2)
    SS_Total = sum((y-np.mean(y))**2)
    r_squared = 1 - (float(SS_Residual))/SS_Total
    adj_r_squared = 1 - (1-r_squared)*(len(y)-1)/(len(y)-X.shape[1]-1)
    return r_squared,adj_r_squared
    
data = pd.DataFrame({"x1": [1,2,3,4,5], "x2": [2,4,6,8,10]})
y = np.array([2.1, 4, 6.2, 8, 9])
model1 = linear_model.LinearRegression()
model1.fit( data.drop("x2", axis = 1),y)
print("model1:", metrics(model1,data.drop("x2", axis=1),y))

model2 = linear_model.LinearRegression()
model2.fit( data,y)
print("model2:", metrics(model2,data,y))

data = pd.DataFrame({"x1": [1,2,3,4,5], "x2": [2.1,4,6.1,8,10.1]} )
y = np.array([2.1, 4, 6.2, 8, 9])
model3 = linear_model.LinearRegression()
model3.fit( data,y)
print("model3:", metrics(model3,data,y))

注：模型1和模型2的预测值相同，因此R²也是相同的，因为R²仅取决于预测值和实际值。

结果如下：

从上表中我们可以看到，即使我们向case 3加入了高度相关的变量，R²仍在增加，而修正R²显示了正确的趋势（即对更多数量的变量惩罚模型2和模型3）

---

调整R²与RMSE的比较

对于前面的例子，我们将看到RMSE在case 1和case 2时相同，类似于R²。在这种情况下，调整后的R²比RMSE做得更好，RMSE的范围仅限于将预测值与实际值进行比较。此外，RMSE的绝对值实际上并不能说明模型有多糟糕。它只能用于比较两个模型，而调整后的R²很容易做到这一点。例如，如果模型的修正R²为0.05，那么它肯定很差。

但是，如果我们只关注预测准确性，那么RMSE是很好的。它计算简单，易于区分，并作为大多数模型的默认度量。

需要再次强调的是，R²的范围并非介于0和1之间， R²的最大值为1，但最小值可为负无穷大。尽管出现负数的可能性不大，但可能性仍然存在。

---

1.5 均方百分比误差 MSPE

让我们考虑以下问题。我们的目标是预测两家商店将销售多少台笔记本电脑？

商店1：预测9，售出10，MSE = 1
商店2：预测999，售出1000，MSE = 1

或者，

商店1：预测9，售出10，MSE = 1
商店2：预测900，售出1000，MSE = 10000

对于前面这种情况，MSE是相同的，我们难以确定谁好谁坏。对于后面这种情况，尽管商店2的MSE非常大，但是900也是很不错了。在这种情况下，我们难以确定谁好谁坏。

这基本上是因为MSE使用绝对平方误差，而相对误差对我们来说更重要。

相对误差偏好可以用均方百分比误差MSPE（Mean Square Percentage Error）表示。对于每个样本，绝对误差除以目标值，给出相对误差。MSPE公式如下：

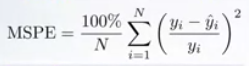
因此，MSPE可以被认为是MSE的加权版本。其样本的权重与其真实的目标平方成反比。

1.6 平均绝对百分比误差 MAPE

相对误差偏好也可以用平均绝对百分比误差MAPE（Mean Absolute Percentage Error）表示。对于每个样本，绝对误差除以目标值，给出相对误差。 MAPE也可以被认为是MAE的加权版本。MAPE的公式如下：

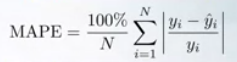
对于MAPE，其样本的权重与其真实的目标成反比。

请注意，如果异常值具有非常非常小的值，则MAPE将非常偏向于它，因为此异常值将具有最高权重。

1.7 均方根平方对数误差 RMSLE

均方根平方对数误差 RMSLE (Root Mean Squared Logarithmic Error)只是以对数标度计算的RMSE。公式如下：

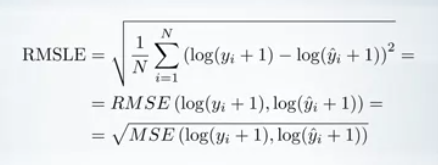
事实上，我们可以看到，采用预测值和目标值的对数，并计算它们之间的RMSE，就是RMSLE 。由于对数函数的自变量只能为正，因此，我们需要加入常数保证为正数，1可以换为其它值。

1.8 解释方差

解释方差（explained_variance_score）又叫可释方差，公式如下：
e x p l a i n e d _ v a r i a n c e ( y , y ^ ) = 1 − V a r { y − y ^ } V a r { y } explained\_{}variance(y, \hat{y}) = 1 - \frac{Var\{ y - \hat{y}\}}{Var\{y\}} explained_variance(y,y^​)=1−Var{y}Var{y−y^​}​

解释方差度量了模型在给定数据集上变化的比例。拟合的越好值越大，最大为1。

1.9 中位数绝对误差 MedAE

中位数绝对误差 MedAE（Median absolute error），公式如下：
$$\text{MedAE}(y,\hat{y})=\text{median}(\mid y_1-{\hat{y}}_1\mid ,\dots ,\mid y_n-{\hat{y}}_n\mid ).$$

可以明显看出来，MedAE对于噪声点是鲁棒的。

二、代码应用

在第一章里，我们几乎列举了所有回归问题中的评价指标，一共有9个。其中，对于大多数评价指标，sklearn中已经有现成的函数了。参看《 Model evaluation: quantifying the quality of predictions》

MAPE和MSPE我们手动实现。

完整代码如下：

from sklearn.metrics import explained_variance_score, mean_absolute_error, \
mean_squared_error,  mean_squared_log_error, median_absolute_error, r2_score
import numpy as np


# 平均绝对百分误差 MAPE
def MAPE(true, pred):
    true = true + 0.1  # 避免0值
    diff = np.abs(np.array(true) - np.array(pred))
    return np.mean(diff / np.abs(true))

# 均方百分比误差 MSPE
def MSPE(true, pred):
    true = true + 0.1  # 避免0值
    diff = np.array(true) - np.array(pred)
    return np.mean(np.power(diff / true, 2))

# 3: fea_nums.具体应用时代入特征数目。这里假设特征数目为3。
def ad_r2(true, pred, fea_nums=3):
  
    SS_Residual = sum((true-pred)**2)
    SS_Total = sum((true-np.mean(true))**2)
    r_squared = 1 - (float(SS_Residual))/SS_Total
    adj_r_squared = 1 - (1-r_squared)*(len(true)-1)/(len(true)-3-1)
    return adj_r_squared

alg_conf = {}
alg_conf["Mmetrics"] = {
    'explained_variance_score:': explained_variance_score,  # 解释方差
    'mean_absolute_error:': mean_absolute_error,  # MAE 
    'mean_squared_error:': mean_squared_error,  # MSE, 
    'mean_squared_log_error': mean_squared_log_error,# MSLE
    'median_absolute_error:': median_absolute_error, # MedAE  
    'r2_score:': r2_score,  # R^2, 
    'MAPE:': MAPE,  # MAPE
    'MSPE:': MSPE,  # MSPE
    'ad_r2:': ad_r2 # 修正r2
    
}

## 真实值和预测值
y_true = np.array([2.1, 4, 6.2, 8, 9])
y_predict = np.array([2, 3.5, 6, 8, 9])

for key, valid_metrics in alg_conf["Mmetrics"].items():
    print(key, valid_metrics(y_true, y_predict))

需要注意的是：RMSE我们对MSE开方即可得到；RMSLE我们对MSLE开方即可得到。

参考文献

【1】Choosing the Right Metric for Evaluating Machine Learning Models — Part 1
【2】机器学习评估指标
【3】修正R方(adjusted R square)是什么？
【4】How to select the Right Evaluation Metric for Machine Learning Models: Part 2 Regression Metrics