Workbench下列车转向架随机振动疲劳分析

随机振动是自然界中普遍存在的一类振动现象，无法通过确定的时间与空间坐标来描述，每一时刻载荷条件无法预测，由于随机振动造成的产品强度破坏、稳定性低、疲劳损伤等问题不容忽视。Workbench下随机振动（Random Vibration）分析在模态叠加法的基础上，从统计学的角度解释了事件发生的概率与能量密度之间的关系，通过叠加各阶模态的贡献来求解系统的响应，支持输入位移谱密度（PSD Displacement）、速度谱密度（PSD Velocity）、加速度谱密度（PSD Acceleration）等作为试验载荷，求解结构的振动响应为产品改进验证提供支撑。疲劳工具（Fatigue Tool）提供了三种随机振动疲劳分析方法，包括窄带（Narrow Band）、斯坦伯格（Steinberg）、Wirsching。下面介绍列车转向架的随机振动与疲劳分析的基本流程，在模态分析的基础上完成随机振动分析。

00

仿真流程

Workbench-nCode

一、前处理

1. 几何模型系统构建

2. 材料模型系统构建

3. 有限元模型系统构建

二、求解

1. 载荷边界条件

2. 位移边界条件

3. 求解设置

三、后处理

1. 求解过程监视

2. 结果量级判定

3. 结果误差分析

01

前处理

Workbench-nCode

1.1 几何模型系统构建

列车转向架的几何模型在DesignModeler中进行简化，如下图1所示，共16个零部件，将所有零件做共节点处理。

图1 弯管模型

1.2 材料模型系统构建

在工程数据库中定义材料模型参数，结构场分析基本参数：密度7850Kg/m3、弹性模量210E9Pa、泊松比0.3，疲劳分析参数：应力-疲劳曲线表（S-N Curve），应力-疲劳曲线如下图2所示，如果没有合适的数据可使用结构钢材料进行分析。

图2 应力-疲劳曲线（S-N Curve）

1.3 有限元模型系统构建

所有模型采用柔性体进行分析，进入到Mechanical之后，所有实体已做共节点处理不再添加连接关系，材料属性为前述自定材料。网格为四面体低阶Solid187单元，其中单元尺寸为40mm，单元数量为72004，节点数量为19078，单元质量分布如下图3所示。

图3 单元质量分布

模态分析无法添加外载荷，若存在初始载荷，可考虑预应力模态。设定列车转向架下部四个圆孔位置添加固定支撑，如下图4所示。

图4 载荷边界与位移边界

求解设定中查找的模态阶数设定为25，此处保证模态的最大频率为输入随机振动中PSD加速度谱最大频率的1.5倍，其余参数保持默认。

完成模态分析的相关设定后，在Workbench界面下搭建随机振动分析流程，如下图5所示，更新结果后重新打开Mechanical界面，完成结果的传递。

图5 随机振动分析流程

02

求解

Workbench-nCode

2.1 载荷边界条件

在随机振动分析环境下添加加速度功率谱PSD Acceleration，对应在表格内输入数据如下表1所示，加速度谱密度曲线如下图6所示。

表1 加速度密度实验谱数据表

图6 加速度密度谱（PSD）

2.2 位移边界条件

模态分析中已设定固定支撑，此处不再设定。

2.3 求解设置

求解设定中一般默认使用所有的模态阶数，输出控制中把计算速度与计算加速度打开，否则无法进行后续的疲劳计算，阻尼控制中常值阻尼一般默认为0.01，其余参数保持默认即可，如下图7所示。设定完成后即可提交计算。

图7 随机振动求解设定

03

后处理

Workbench-nCode

3.1 求解过程监视

频域上的统计计算，软件很快计算完成。

3.2 结果量级判定

计算结果并不是一个数值，它表示在给定的概率（1 Sigma/2 Sigma/3 Sigma）时间相应内小于标准值。对应的概率可参考正太分布函数，其中±1 Sigma、±2 Sigma、±3 Sigma水平对应的概率如下图8所示。

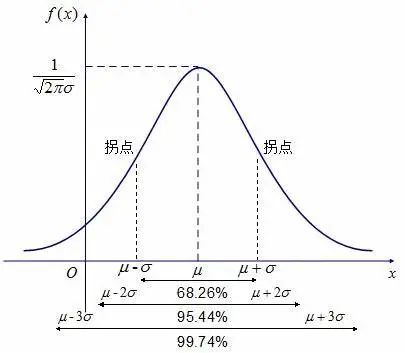
图8 正态分布函数

3.3 结果误差分析

结果中查看Y方向3Sigma时间响应内变形小于的标准值，如下图9所示，最大变形发生在列车转向架中部为0.56891mm。表明在给定的PSD加速度试验谱条件下，在99.73%响应时间内变形小于标准值0.56891mm。

图9 3Sigma下Y方向变形结果

结果中查看Y方向3Sigma时间响应内等效应力小于的标准值，如下图10所示，可以看到最大应力为37.253MPa，发生在列车转向架中间轴与两侧横梁之间的过渡位置，表明在给定的PSD加速度试验谱条件下，在99.73%响应时间内等效应力小于标准值37.253MPa。

图10 3Sigma下等效应力结果

结果中添加功率谱响应工具（Response PSD Tool），可以查看几何体以及远程点上的功率谱密度，如下图11所示，这里查看几何体上某一硬点的加速度功率谱密度响应曲线，如下图12所示。表明在给定的PSD加速度试验谱作为激励条件下，该点产生的响应中最大加速度为1.4215e9 [(mm/s2)2/Hz]，若有条件可通过实验进行对比。

图11 功率谱响应工具（Response PSD Tool）

图12 几何体硬点Y方向的加速度功率谱密度响应情况

结果中添加疲劳工具（Fatigue Tool），查看列车转向架的疲劳寿命情况，这里采用窄带的寿命假设理论，曝光时间为1s指明计算出的疲劳寿命的基本单位是秒，寿命结果如下图14所示，可以看到最大寿命为1e35s，最小寿命为2.3542e18s，注意单位制，可再次基础上将其转换为小时或天。

图13 疲劳工具（Fatigue Tool）

图14 疲劳-寿命结果（Life）