ArcGIS学习20：基于成本栅格数据的空间路径分析

基于成本栅格数据的空间路径分析

---

---

前言

本文基于立方数据院学习平台的学习，介绍构建成本权重栅格数据、基于成本栅格求解最低成本路径、批量求解多起点到多终点的最低成本路径。

---

一、基本原理与思路

1.1 核心要点

设置起点与终点
构建成本权重栅格数据
实现最短路径路线图

1.2 基本概念

源: 指距离分析中的目标或目的地
成本:指从起点到终点过程中所需要花费的成本，包括了时间、金钱等。影响成本的要素可以是单个也可以是多个
成本距离加权数据: 通过量化多个成本指标，最后按照一定权重比例叠加的结果。也就是被量化之后的最终成本数据距离方向数据:表示从每一个单元格出发，沿着最低累计成本路径达到最近目标的路线方向。
①(a)图代表成本距离加权数据
②(b)图代表方向数据
③©图代表每个单元格的方向值数据

1.3 距离分析工具（主要）

• 成本路径
  ①生成距离栅格数据
  ②生成回溯链接栅格数据
• 成本路径
  生成成本路径栅格数据
• 欧氏距离
  生成距离栅格数据

1.4 分析思路

数据认知
起点和终点/地形栅格数据/湾斑块/河流水域/现状道路
构建成本权重栅格数据
定义/量化 最低成本 → 什么是最低成本?
①尽量现状道路进行
②避开河流水域
③尽量靠近村湾建设用地
④坡度越小的地方成本越低

成本加权
叠加数据 = (“道路指标”*0.3+ “建设用地指标”*0.3+“坡度指标”*0.4 ) +“水域指标”
①“道路指标”:0-10
②“建设用地指标”:0-10
③坡度指标” :0-10
④“水域指标”:10

由于水域是决定性指标，因此其指标数量较大。

二、构建成本栅格数据

2.1 环境设置

2.2 坡度因素

表面分析，生成坡度


重分类: 按照标准分为10类
重点: 坡度越小成本越低!


更改布局并增加图例

2.3 建设用地因素

欧氏距离
重分类: 相等的间隔分为10类
重点:距离越近成本越低 !

2.4 水域因素

要素转栅格

判断是否有空值



重分类
0表示有水（10分），1表示无水（0分）

2.5 道路因素

道路等级赋分

要素转栅格

判断是否有空值

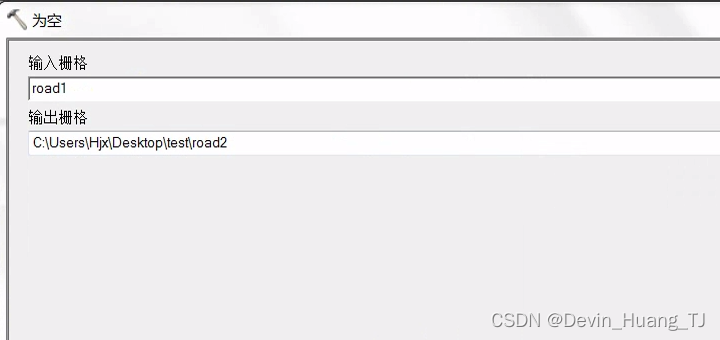
综合取值

2.6 计算加权

叠加数据= (“道路指标”*0.3+ “建设用地指标”*0.3+“坡度指标”*0.4)+“水域指标”

三、基于成本栅格数据求解最低成本路径

基于栅格成本生成最低成本路径使用的工具为“成本路径”。在“成本路径”工具的输入要素中要求“输入成本距离栅格数据”和“输入成本回溯链接栅格数据”。

这两个数据需要我们使用到另外一个工具“成本距离”来得到。

3.1 利用成本距离工具得到成本距离栅格数据和成本回溯链接栅格数据

加载起点、终点数据
加载数据

构建距离成本
以起点开始计算“成本距离


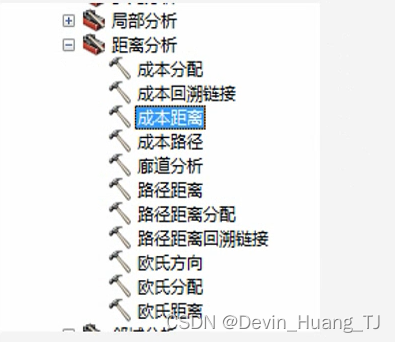
成本距离

成本方向

3.2 使用“成本路径”工具得到最低成本路径

实现最短路径路线图
生成路径


生成路径 多个终点时的情况

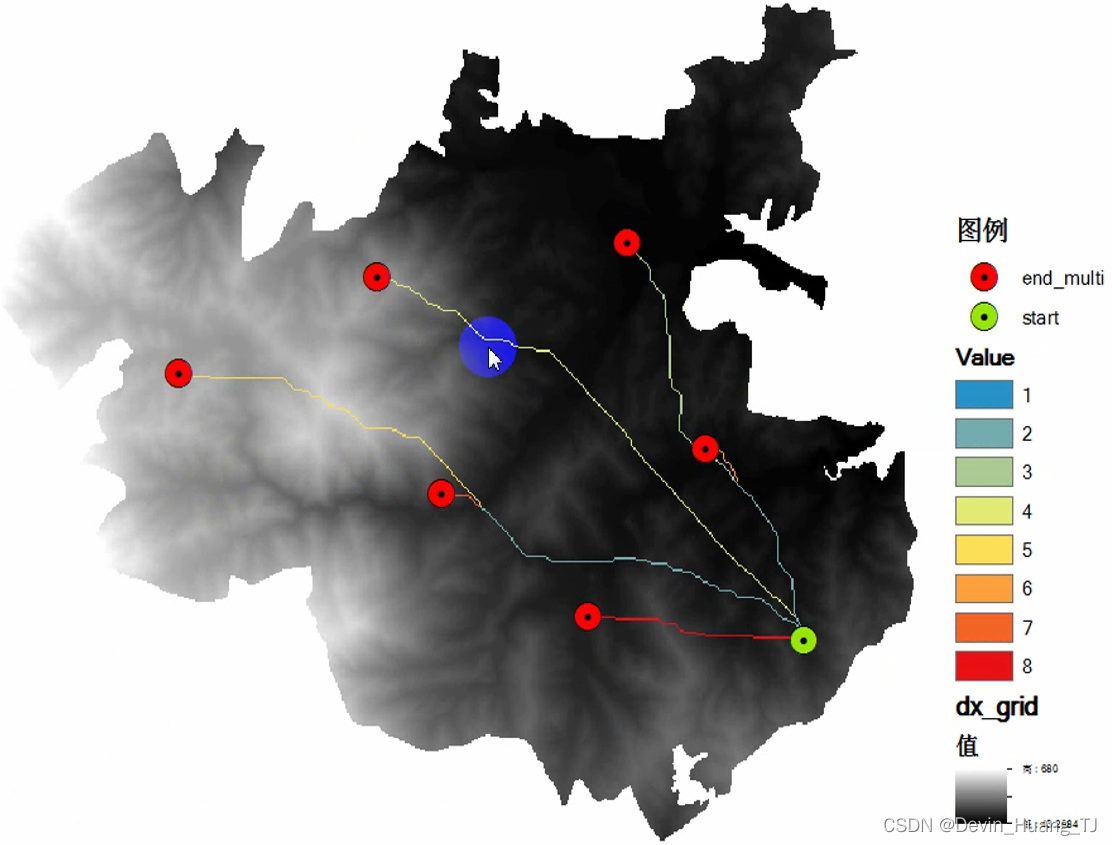
将栅格格式的路径转出

四、批量求解多起点到多终点的最低成本路径

4.1 多起点多终点生成路径网路

构建模型

起点连接迭代要素器（按ID分组）

起点数据作为要素源，成本数据作为成本连接成本距离工具

距离作为成本栅格数据，方向作为成本回溯链接栅格数据，终点作为输入要素连接成本路径工具

连接栅格转折线工具（行内变量替换）

合并线路

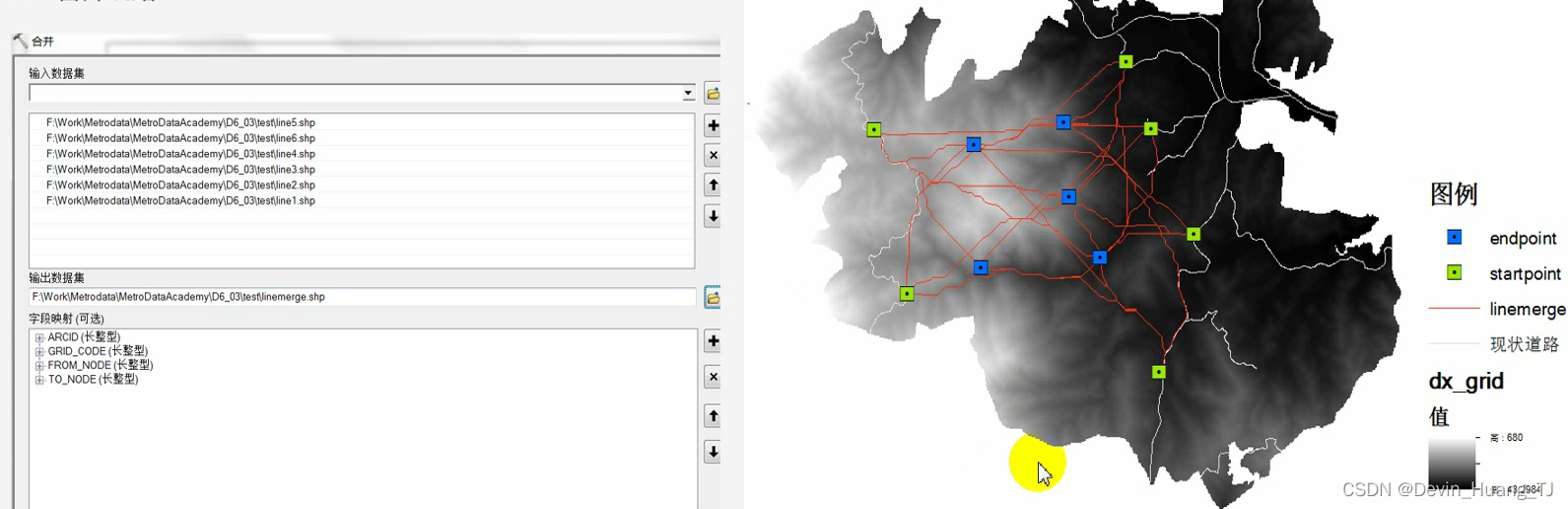
4.2 路径3D效果的可视化

等值线设置并浮在表面

加载路径和起终点，并浮于表面

总结来说，基于成本栅格数据计算最低成本路径是一种空间选线方法，比如绿道选线，河流选线等。其在工具操作上并不复杂，关键点在于要根据分析目标构建出合理的成本栅格数据。

---

总结