通俗理解Hessian矩阵的几何意义

先用一个不精确的通俗的例子来说明：

①初中数学里面的$f(x)=\frac{1}{2}A{x}^2-bx+c$
显然我们知道A>0时，$f(x)$才有最小值。

②再来看三维:
$f(x)=\frac{1}{2}{x}^{T}Ax-b^{T}x+c$
当A正定时，f(x)才有唯一最小值。(当然了，这里的$b^T$前面的符号也可以是+,这并不影响结论)

正定的意思其实就是：定义的变量取值为正。

负定的意思其实就是：定义的变量取值为负。

为了清晰对比，我们把他们放在表格里面：

表达式	对最高次系数的要求	x性质	几何性质
$f(x)=\frac{1}{2}A{x}^2-bx+c$	A>0	标量	二维，平面抛物线，具有唯一最小值
$f(x)=\frac{1}{2}{x}^{T}Ax-b^{T}x+c$	A正定	矢量$x=(x1,x2{)}^T$	三维，向下凸的椭圆面，具有唯一最小值

发现规律没？

其实三维中的正定这个东西的含义，仅仅是为了"对标"二维中的唯一且最小的这两个条件。

正定其实是为了满足几何特性而服务的。

关于唯一且最小，下面我们使用matlab来比较:

正定矩阵、半正定矩阵、不定矩阵、负定矩阵、半负定矩阵的几何图形到底有什么区别：

表达式	矩阵A(2x2,每2个换行)	矩阵性质	对应的空间曲面	效果
$f(x)=x_1^2+x_2^2+0.1x_1{x}_2$	$\left[\begin{array}{cc}1& 0.05\\ 0.05& 1\end{array}\right]$	正定		具有唯一的最小值
$f(x)=x_1^2+x_2^2+2x_1{x}_2$	$\left[\begin{array}{cc}1& 1\\ 1& 1\end{array}\right]$	半正定		具有不唯一的最小值(最小值是一条线)
$f(x)=x_1^2+x_2^2+4x_1{x}_2$	$\left[\begin{array}{cc}1& 2\\ 2& 1\end{array}\right]$	不定矩阵		存在鞍点，无最小值点，也无最大值点
$f(x)=-x_1^2-x_2^2+0.1x_1{x}_2$	$\left[\begin{array}{cc}-1& 0.05\\ 0.05& -1\end{array}\right]$	不定矩阵		具有唯一的最大值
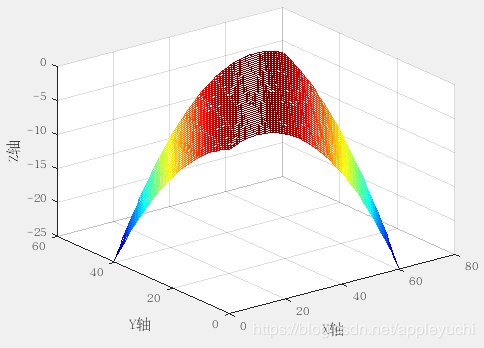$f(x)=-x_1^2-x_2^2+2x_1{x}_2$	$\left[\begin{array}{cc}-1& 1\\ 1& -1\end{array}\right]$	半负定矩阵		具有不唯一的最大值(最大值是一条线)
$f(x)=-x_1^2-x_2^2+0.2x_1{x}_2$	$\left[\begin{array}{cc}-1& 0.1\\ 0.1& -1\end{array}\right]$	负定矩阵		具有唯一的最大值

注意，负定矩阵的定义式：

若矩阵A是n阶负定矩阵，则A的偶数阶顺序主子式大于 0，奇数阶顺序主子式小于 0。

而正定矩阵的定义是：

计算A的各阶主子式。若A的各阶主子式均大于零，则A是正定的；

－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－

另外可以看到，对于不定矩阵而言，仅仅靠特征值以及正负定情况是无法直接判断是否存在唯一的最大/最小值的。

以负定矩阵为例，上述表格中的matlab的绘图代码如下：

colormap Jet
% ###########################
[x,y]=meshgrid(-3:0.1:3,-2:0.1:2);
subplot(2,2,1),mesh(z1)
z1=(-x.^2-y.^2+0.1*x.*y);
subplot(2,2,1),mesh(z1)
x=xlabel('X轴');
y=ylabel('Y轴');        %y轴标题
z=zlabel('Z轴');        %z轴标题

为什么要研究曲线的最小值和最大值呢？

因为hessian矩阵是由神经网络的各种系数组成的矩阵，

hessian矩阵正定，则空间曲线有最小值，则目标函数有最小值，则拟合最佳。

目标函数一般是误差函数,不考虑过拟合和欠拟合的情况下目标函数的最小值是我们的追求目标，

所以要研究hessian矩阵的正定性和鞍点。

注意：

概念上而言，不定矩阵≠非正定矩阵≠非负定矩阵