Coursera_ Algorithms I 学习笔记：Module_3_Analysis_of_Algorithm_Introduction

我叫王棱夹

于 2024-09-29 16:00:34 发布

阅读量785

点赞数 9

文章标签：学习笔记算法

本文链接：https://blog.csdn.net/approximately_/article/details/142637504

版权

Coursera_ Algorithms I 学习笔记：Module_3_Analysis_of_Algorithm_Introduction

scientific method applied to analysis of algorithms

data analysis

log-log plot

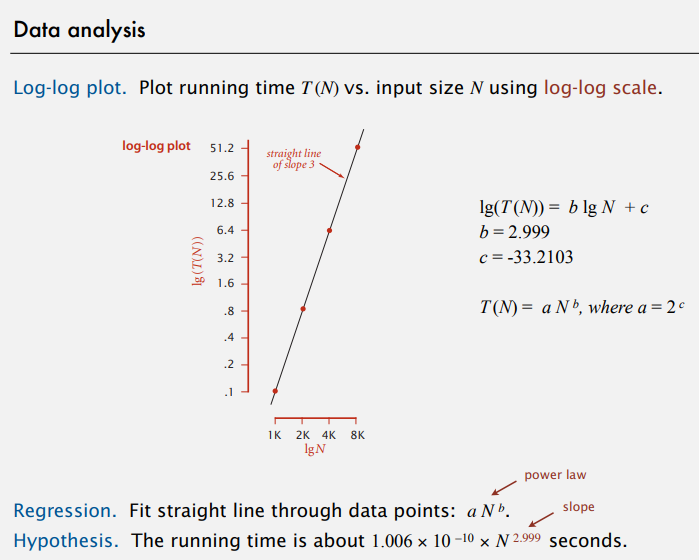
doubling hypothesis

experimental alogrithmics

System independent effects
System dependent effects

some costs of basic operations

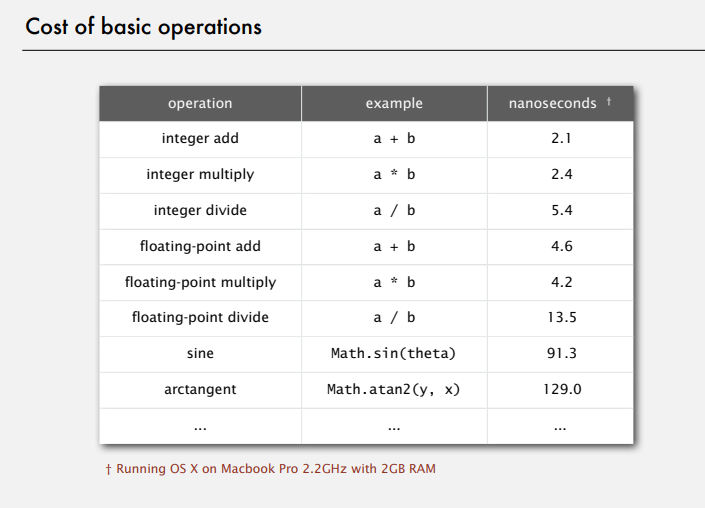
tilde notation

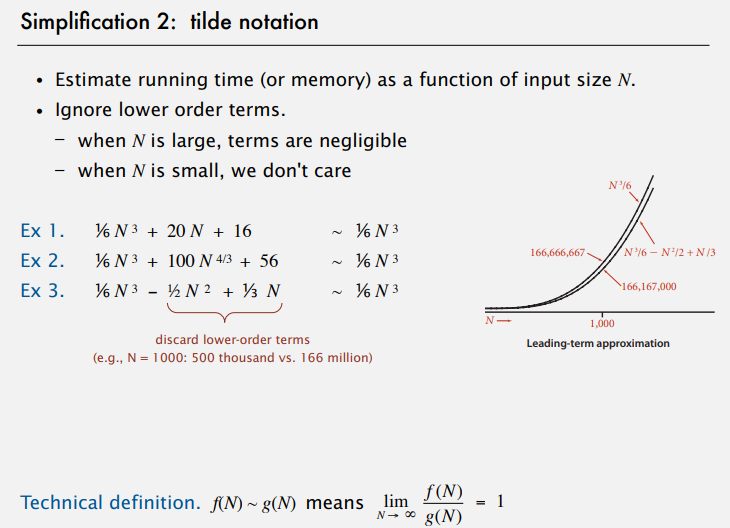
use calculus to estimate a discrete sum

Here I have a question: why Ex1. the result using sum equation is equal to the one using the calculus ???

Euler-Maclaurin公式——用连续和估计离散和

mathematical models for running time

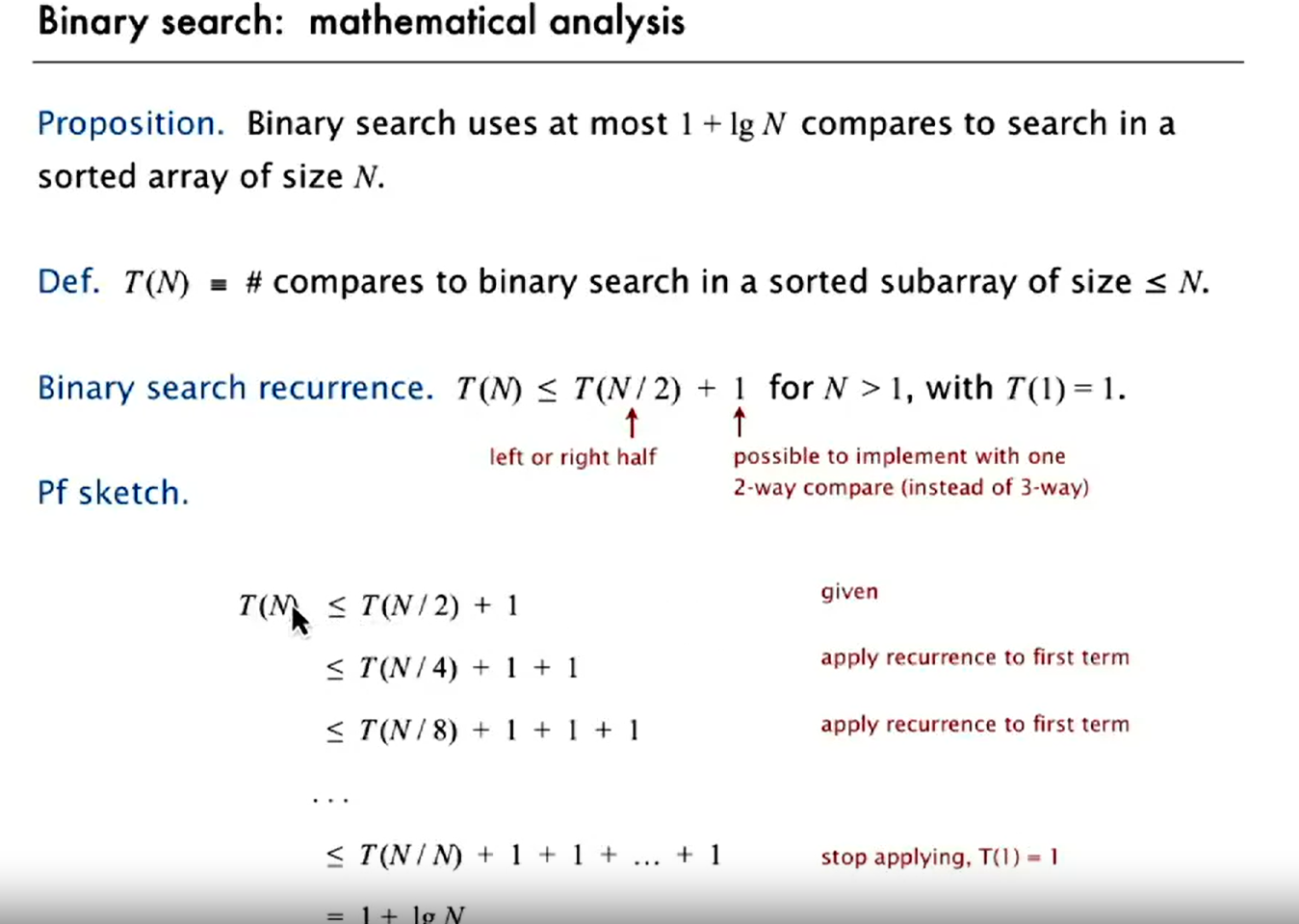
binary search

proof to binary search

Comparing programs between sorting-base algorithm and brute-force algorithm

Theory of alogrithms

Types of analyses

best case
worst case
average case

An order of growth is a set of functions whose asymptotic growth behavior is considered equivalent. For example, 2n, 100n and n+1 belong to the same order of growth, which is written O(n) in Big-Oh notation and often called linear because every function in the set grows linearly with n.

commonly-used notations in the theory of alogrithms

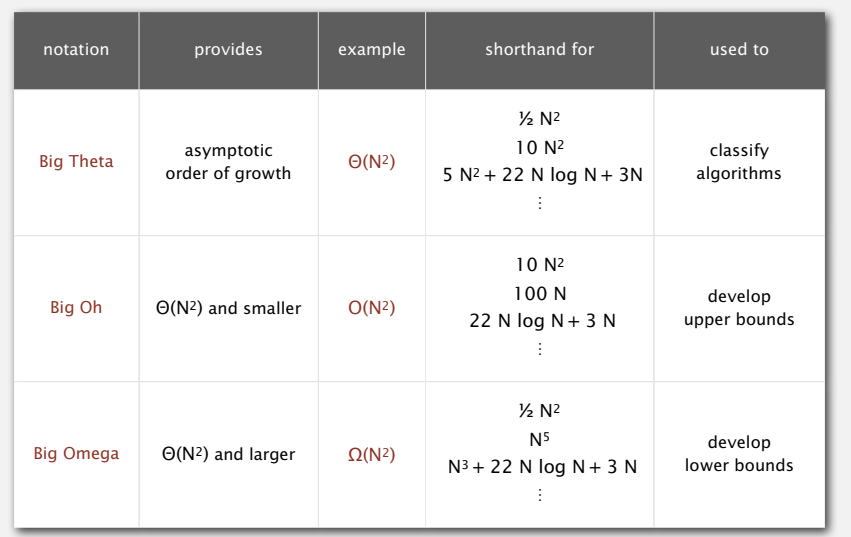
时阳光老师的课件上有形式化的描述

algorithm design approach

这句话的意思是，算法理论中有很多已发表的研究，许多人误解了大O符号的结果。大O符号通常用于提供问题难度的改进上界，而不是作为运行时间的近似模型。换句话说，虽然大O表示了算法在最坏情况下的复杂度，但它并不一定能准确预测实际运行时间，因此将其当作实际运行时间的近似是一个错误。

Memory

typical memory usage for primitive types and arrays

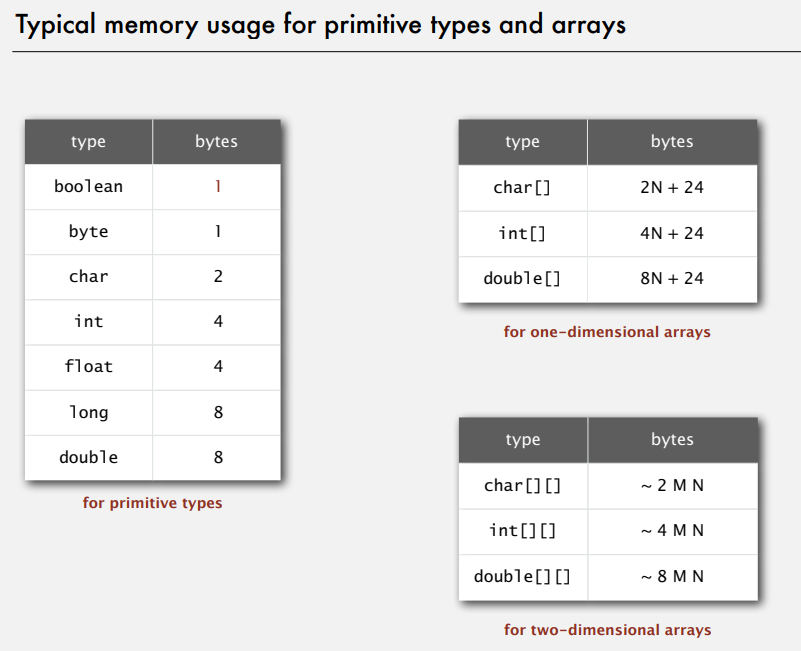
typical memory usage summary

Shallow memory usage: Don’t count referenced objects.
Deep memory usage: If array entry or instance variable is a reference, add memory (recursively) for referenced object

example

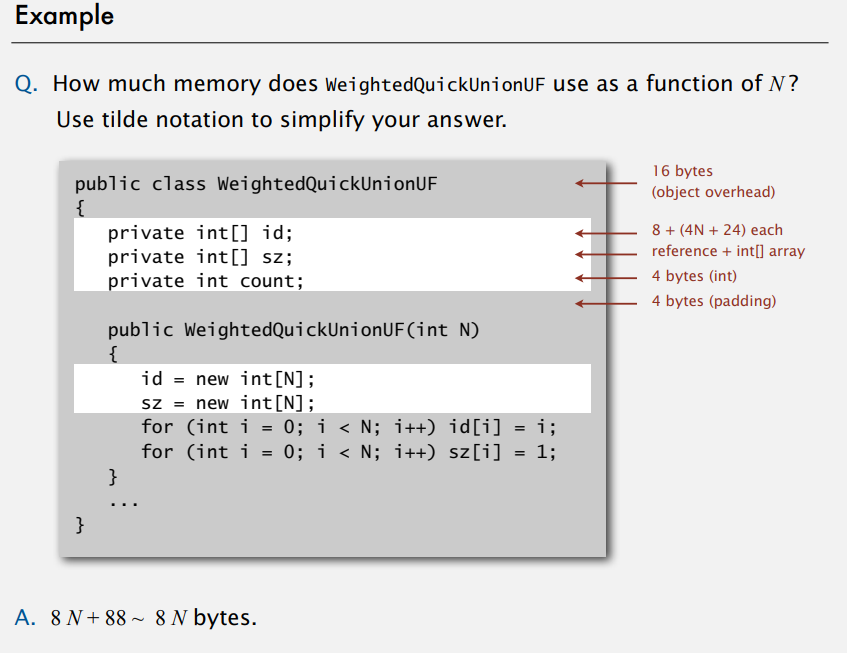
二次时间内解决3-SUM问题

关于复杂度这里有一点需要说明：内层循环的运行次数是n-1 + n-2 + n-3 + …… + 2 + 1，求和可知整个循环的时间复杂度是O(n^2)

search in a bitonical array

answer

要在一个比特尼克数组中搜索一个整数，可以使用修改过的二分查找方法。下面是实现的思路和代码示例：

标准版本：约 (3 \lg n) 次比较

找到峰值：首先，找到比特尼克数组的峰值（最大元素）。可以通过修改二分查找在 ( O(\lg n) ) 时间内完成。
在两部分中查找：
在递增部分使用标准的二分查找。
在递减部分使用标准的二分查找。

示例代码（Python）：
def find_peak(arr):
    left, right = 0, len(arr) - 1
    while left < right:
        mid = (left + right) // 2
        if arr[mid] > arr[mid + 1]:
            right = mid  # 在左侧部分查找
        else:
            left = mid + 1  # 在右侧部分查找
    return left  # 返回峰值索引

def binary_search(arr, left, right, target, ascending=True):
    while left <= right:
        mid = (left + right) // 2
        if arr[mid] == target:
            return mid
        if ascending:
            if arr[mid] < target:
                left = mid + 1
            else:
                right = mid - 1
        else:
            if arr[mid] > target:
                left = mid + 1
            else:
                right = mid - 1
    return -1

def search_bitonic_array(arr, target):
    peak_index = find_peak(arr)
    # 在递增部分查找
    index = binary_search(arr, 0, peak_index, target, ascending=True)
    if index != -1:
        return index
    # 在递减部分查找
    return binary_search(arr, peak_index + 1, len(arr) - 1, target, ascending=False)

# 示例
bitonic_array = [1, 3, 8, 12, 4, 2]
target = 4
result = search_bitonic_array(bitonic_array, target)
print(result)  # 输出目标元素的索引
签名奖金版本：约 (2 \lg n) 次比较

直接搜索而不单独寻找峰值：我们不单独找到峰值，而是在搜索目标元素的同时利用比特尼克数组的性质。

二分查找的修改：
先进行标准的二分查找，检查中间元素。
如果中间元素等于目标，直接返回。
如果中间元素大于其右邻居（说明在递增部分），则继续在左半部分和右半部分分别进行递归搜索。
如果中间元素小于其右邻居，则说明在右半部分，继续在右半部分和左半部分分别进行递归搜索。

具体步骤
开始搜索：

设置初始的左右边界 left 和 right。
在每次迭代中计算中间索引 mid。
比较并搜索：
如果 arr[mid] == target，返回 mid。
如果
mid
不是峰值：
如果
arr[mid] < arr[mid + 1]
，说明在递增部分：

先在递增部分搜索 left 到 mid，然后再在递减部分搜索 mid + 1 到 right。
如果
arr[mid] > arr[mid + 1]
，说明在递减部分：

先在递减部分搜索 mid 到 right，然后再在递增部分搜索 left 到 mid - 1。
示例代码
def binary_search_bitonic(arr, left, right, target):
    if left > right:
        return -1

    mid = (left + right) // 2
    
    # 检查中间元素
    if arr[mid] == target:
        return mid

    # 如果 mid 不是峰值
    if mid < len(arr) - 1 and arr[mid] < arr[mid + 1]:
        # 在递增部分查找
        result = binary_search_bitonic(arr, left, mid - 1, target)
        if result != -1:
            return result
        # 在右侧部分查找
        return binary_search_bitonic(arr, mid + 1, right, target)
    else:
        # 在递减部分查找
        result = binary_search_bitonic(arr, mid + 1, right, target)
        if result != -1:
            return result
        # 在左侧部分查找
        return binary_search_bitonic(arr, left, mid - 1, target)

def search_bitonic_array(arr, target):
    return binary_search_bitonic(arr, 0, len(arr) - 1, target)

# 示例
bitonic_array = [1, 3, 8, 12, 4, 2]
target = 4
result = search_bitonic_array(bitonic_array, target)
print(result)  # 输出目标元素的索引
证明 (2 \lg n) 次比较的下限

对于比特尼克数组，任何搜索算法的比较次数至少要对数级别的，即每次比较都能排除一半的元素。由于我们在一个数组中进行两次查找（递增和递减），因此最坏情况下的比较次数是 (2 \lg n)。这是因为在最佳情况下，每次比较会将待查找元素范围减半，两个阶段的查找叠加导致了这个下限。

希望这能帮助你理解如何在比特尼克数组中搜索一个整数！如果有其他问题，欢迎提问。

扔鸡蛋问题

好的，接下来我们详细解释 Version 2 到 Version 4 的算法思路：

Version 2: (\sim \lg T) 个鸡蛋和 (\sim 2 \lg T) 次投掷

思路：

这个版本要求你用 ( \lg T ) 个鸡蛋，在 ( 2 \lg T ) 次投掷内找到鸡蛋破裂的临界楼层 ( T )。算法分两步：

找到包含 ( T ) 的区间：

你需要首先找到一个大小为 ( 2T ) 的区间，也就是从第 1 层到第 ( 2T ) 层。如果你知道了这个区间，你可以确定 ( T ) 肯定在这个范围内。
为了找到这个区间，你可以采用指数增长的方法：从第 1 层开始，每次增加一倍，直到鸡蛋破裂为止。
例如，先从第 1 层投掷，再从第 2 层、接着是第 4 层、8 层、16 层……直到某次投掷时鸡蛋破裂。

这样，你找到一个区间 ( [2^{k-1}, 2^k] )，确保 ( T ) 在这个区间内。

在区间中做二分查找：

找到区间后，接下来可以用二分查找的方式来缩小范围。因为区间大小是 ( 2T )，在最坏情况下，二分查找会用 ( \lg T ) 次投掷找到临界楼层。
在此过程中，你用了一次鸡蛋在第一步找区间，剩下的鸡蛋在第二步做二分查找。

总结：

步骤 1：使用指数增长找到 ( T ) 所在的区间（约 ( \lg T ) 次投掷）。
步骤 2：在区间内用二分查找（约 ( \lg T ) 次投掷）。
整体算法在最坏情况下需要 ( 2 \lg T ) 次投掷。

Version 3: 2 个鸡蛋和 (\sim 2 \sqrt{n}) 次投掷

思路：

这个版本中只有两个鸡蛋，并且目标是在 ( 2\sqrt{n} ) 次投掷内找到临界楼层 ( T )。这里的思路是分段逐步查找。

找到大小为 ( \sqrt{n} ) 的区间：

由于只有 2 个鸡蛋，如果第一个鸡蛋破了，我们只能线性搜索剩余的楼层。因此，不能每次只上升一层投掷，而是每次跳过一个区间大小为 ( \sqrt{n} ) 的楼层。
具体步骤是：从第 ( \sqrt{n} ) 层开始投掷，第 ( 2\sqrt{n} ) 层、第 ( 3\sqrt{n} ) 层……直到鸡蛋破裂。
如果鸡蛋在某次投掷时破裂，那么 ( T ) 必然位于上一组区间内。

在找到的区间中线性搜索：

一旦鸡蛋破裂，我们就在上一个区间（例如从 ( (k-1)\sqrt{n} ) 到 ( k\sqrt{n} )）中逐层搜索，使用线性查找找到 ( T )。

总结：

步骤 1：每次跳过 ( \sqrt{n} ) 楼层进行投掷，直到鸡蛋破裂。这个过程大约需要 ( \sqrt{n} ) 次投掷。
步骤 2：一旦鸡蛋破裂，在确定的区间内线性查找，最多需要 ( \sqrt{n} ) 次。
因此，总共大约需要 ( 2\sqrt{n} ) 次投掷。

Version 4: 2 个鸡蛋和 ( \leq c\sqrt{T} ) 次投掷

思路：

这个版本中你仍然只有 2 个鸡蛋，但目标是限制在 ( c\sqrt{T} ) 次投掷内找到 ( T )，其中 ( c ) 是常数。

逐步增加搜索范围：

在这种情况下，你从第 1 层开始，逐步递增楼层数进行投掷。你先从第 1 层投掷，然后第 3 层，再第 6 层，接着第 10 层……也就是每次递增的楼层数是逐步增加的：1, 2, 3, 4, 5…。
这种方式确保你不会跳过可能的临界楼层 ( T )，并且能够有效减少总的投掷次数。

线性查找：

一旦鸡蛋破裂，你只需要在线性递增到的上一层开始线性查找即可。因为你是逐步递增的，所以不会跳过任何可能的临界楼层。

总结：

这种方法的最大投掷次数是 ( 1 + 2 + 3 + … + t )，其中 ( t ) 是你最终达到的楼层。因此总的投掷次数约为 ( \frac{t(t + 1)}{2} )，满足 ( t \sim \sqrt{T} )。
这意味着你总共需要 ( O(\sqrt{T}) ) 次投掷，并且 ( c ) 是一个常数，可以调整使得投掷次数符合题目要求。

总结：

Version 2 利用二分查找，先找到包含 ( T ) 的区间，然后在区间内做二分查找，总共需要 ( 2 \lg T ) 次投掷。
Version 3 通过每次跳 ( \sqrt{n} ) 楼层进行投掷，一旦鸡蛋破裂，在线性搜索剩余区间，总共需要 ( 2\sqrt{n} ) 次投掷。
Version 4 使用逐层递增的方式寻找 ( T )，投掷次数大约是 ( O(\sqrt{T}) )，总共 ( c\sqrt{T} ) 次投掷。

如果还有进一步的疑问或需要代码实现，可以继续告诉我！