从决策树到GBDT梯度提升决策树和XGBoost

最新推荐文章于 2024-09-23 12:50:51 发布

小鹅鹅

最新推荐文章于 2024-09-23 12:50:51 发布

阅读量4.6k

点赞数

分类专栏：机器学习推荐系统算法入门文章标签：决策树数据挖掘

本文链接：https://blog.csdn.net/asd136912/article/details/78556362

版权

机器学习同时被 2 个专栏收录

14 篇文章 3 订阅

订阅专栏

推荐系统算法入门

7 篇文章 6 订阅

订阅专栏

从决策树到GBDT(Gradient Boosting Decision Tree)梯度提升决策树和XGBoost的一些学习笔记

决策树

决策树可以转换成if-then规则的集合，也可以看作是定义在特征空间划分类的条件概率分布。决策树学习算法包括三部分：特征选择，数的生成和数的剪枝。最大优点: 可以自学习。在学习的过程中,不需要使用者了解过多背景知识,只需要对训练实例进行较好的标注,就能够进行学习。显然,属于有监督学习。
常用有一下三种算法：

ID3 — 信息增益最大的准则
C4.5 — 信息增益比最大的准则
CART(Classification and Regression tree, 分类与回归树)
回归树: 平方误差最小的准则
分类树: 基尼系数最小的准则

回归树 Regression Decision Tree

回归树总体流程类似于分类树，区别在于，回归树的每一个节点都会得一个预测值。

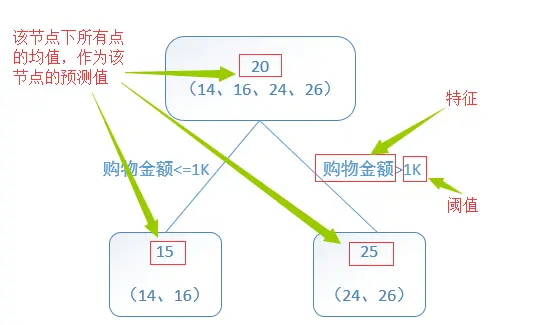
使用平方误差最小准则
训练集为：D={(x1,y1), (x2,y2), …, (xn,yn)}。
输出Y为连续变量，将输入划分为M个区域，分别为R1,R2,…,RM,每个区域的输出值分别为：c1,c2,…,cm则回归树模型可表示为：

f (x) = \sum m = 1 M c m I (x \in R m)

$f(x)=\sum^M_{m=1}c_mI(x\in R_m)$
接下来可以使用平方误差

∑xi∈Rm(yi−f(xi)) ∑ x i ∈ R m ( y i − f ( x i ) ) $\sum_{x_i\in Rm}(y_i-f(x_i))$ 来表示训练数据的预测误差，用最小平方误差的准则来求解每个单元的最优输出值。

c^m = a v e (y i | x i \in R m)

$\hat c_m=ave(y_i|x_i\in R_m)$
假如使用特征j的取值s来将输入空间划分为两个区域，分别为：

R 1 (j, s) = {x | x (j) < = s} 和 R 2 (j, s) = {x | x (j) > s}

$R_1(j,s)=\{x|x^{(j)}<=s\}和R_2(j,s)=\{x|x^{(j)}>s\}$
选择最优切分变量j与切分点s，求解

min j, s [min c 1 \sum x i \in R 1 (j, s) (y i - c 1) 2 + min c 2 \sum x i \in R 2 (j, s) (y i - c 2) 2]

$\min_{j,s}[\min_{c_1} \sum_{x_i\in R_1(j,s)}(y_i-c_1)^2 + \min_{c_2} \sum_{x_i\in R_2(j,s)}(y_i-c_2)^2]$
并可以得出

c^1 = a v e (y i | x i \in R 1 (j, s))

$\hat c_1=ave(y_i|x_i\in R_1(j,s))$

c^2 = a v e (y i | x i \in R 2 (j, s))

$\hat c_2=ave(y_i|x_i\in R_2(j,s))$

最小二叉回归树生成算法：

从以上可以归纳出在最小二叉回归树生成算法。训练数据集所在的输入空间中，递归地将每个区域划分为两个子区域并决定每个子区域上输出值，构建二叉决策树。
1. 选择最优切分变量j与切分点s，求解

min j, s [min c 1 \sum x i \in R 1 (j, s) (y i - c 1) 2 + min c 2 \sum x i \in R 2 (j, s) (y i - c 2) 2]

$\min_{j,s}[\min_{c_1} \sum_{x_i\in R_1(j,s)}(y_i-c_1)^2 + \min_{c_2} \sum_{x_i\in R_2(j,s)}(y_i-c_2)^2]$
遍历变量j，对固定的切分变量j扫描切分点s，选择使上式最小值的对(j,s)。其中Rm是被划分的输入空间，cm是空间Rm对应的固定输出值。
2. 用选定的对(j,s)划分区域并决定相应的输出值：

R1(j.s)={x∣x(j)≤s},R2(j,s)={x∣x(j)>sc^m=1Nm∑xi∈Rm(j,s)yi,x∈Rm,m=1,2 R 1 ( j . s ) = { x ∣ x ( j ) ≤ s } , R 2 ( j , s ) = { x ∣ x ( j ) > s c ^ m = 1 N m ∑ x i ∈ R m ( j , s ) y i , x ∈ R m , m = 1 , 2

$R_1(j.s)=\lbrace x\mid x^{(j)} \le s \rbrace , \quad R_2(j,s)=\lbrace x\mid x^{(j)}\gt s \\ \hat c_m = {1\over N_m}\sum_{x_i\in R_m(j,s)}y_i , \quad x\in R_m , m=1,2$
3. 继续对两个子区域调用步骤（1），（2），直至满足停止条件。
4. 将输入空间划分为M个区域R1,R2,…,RM，生成决策树：

f (x) = \sum m = 1 M c^m I (x \in R)

$f(x) = \sum_{m=1}^M\hat c_m I(x\in R)$

提升树 Boosting Decision Tree

提升树是迭代多棵回归树来共同决策。当采用平方误差损失函数时，每一棵回归树学习的是之前所有树的结论和残差，拟合得到一个当前的残差回归树，残差的意义如公式：残差 = 真实值 - 预测值。提升树即是整个迭代过程生成的回归树的累加。

提升树的核心就在于，每一棵树学的是之前所有树结论和的残差，这个残差就是一个加预测值后能得真实值的累加量。比如A的真实年龄是18岁，但第一棵树的预测年龄是12岁，差了6岁，即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习，如果第二棵树真的能把A分到6岁的叶子节点，那累加两棵树的结论就是A的真实年龄；如果第二棵树的结论是5岁，则A仍然存在1岁的残差，第三棵树里A的年龄就变成1岁，继续学。这就是Boosting的意义。

提升树/GBDT的常用损失函数如图，如何选择损失函数决定了算法的最终效果，包括用平方误差损失函数的回归问题，指数损失函数的分类问题，以及用一般损失函数的一般决策问题。

对于二分类问题，提升树算法只需将AdaBoost算法中的基本分类器限制为二类分类树即可，可以说此时提升树算法是AdaBoost的特殊情况。这里简单叙述一下回归问题的提升树算法。

提升树算法

$\{ \\ \quad\, 输入：训练数据集D=\{(x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), \cdots, (x^{(M)}, y^{(M)})\}, x^{(i)} \in \mathcal{X} \subseteq R^n, y^{(i)} \in \mathcal{Y}; \\ \quad 输出：提升树f_K(x). \\ \quad 过程: \\ \qquad (1). 初始化模型f_0(x) = 0； \\ \qquad\; (2). 循环训练K个模型 k=1,2,\cdots,K \\ \qquad\qquad (a). 计算残差：r_{ki} = y^{(i)} - f_{k-1}(x^{(i)}), \quad i=1,2,\cdots,M \\ \qquad\qquad (b). 拟合残差r_{ki}学习一个回归树，得到T(x;\Theta_k) \\ \qquad\qquad (c). 更新f_k(x) = f_{k-1}(x) + T(x; \Theta_k) \\ \qquad\; (3). 得到回归提升树 \\ \qquad\qquad f_K(x) = \sum_{k=1}^{K} T(x; \Theta_k) \\ \}$

梯度提升决策树 Gradient Boosting Decision Tree (GBDT)

提升树利用加法模型和前向分步算法实现学习的优化过程。当损失函数时平方损失和指数损失函数时，每一步的优化很简单，如平方损失函数学习残差回归树。但对于一般的损失函数，往往每一步优化没那么容易，如下图中的绝对值损失函数和Huber损失函数。针对这一问题，Freidman提出了梯度提升算法：利用最速下降的近似方法，即利用损失函数的负梯度在当前模型的值，作为回归问题中提升树算法的残差的近似值，拟合一个回归树。

步骤:

求出损失函数的负梯度, 当做残差的近似值。
然后让一棵树去拟合每个样本的残差。
- 回归树和决策树很类似，只是回归树把落入叶子节点的样本，对于他们的标签求了个平均值输出，注意，这里的标签，对于GBDT来说，是每一个样本的残差。
然后再去求这棵树的占的比重。估计回归树叶节点区域，以拟合残差的近似值。
线性搜索求系数, 也就是每棵树的系数，使损失函数极小化
最后的模型用这些树融合

梯度提升GBDT算法：

$\{ \\ \quad\, 输入：训练数据集D=\{(x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), \cdots, (x^{(M)}, y^{(M)})\}, x^{(i)} \in \mathcal{X} \subseteq R^n, y^{(i)} \in \mathcal{Y}; \\ \qquad\quad\; 损失函数L(y, f(x)); \\ \quad 输出：提升树\hat{f}(x). \\ \quad 过程: \\ \qquad (1). 初始化模型 \\ \qquad\qquad\qquad f_0(x) = \arg \min_c \sum_{i=1}^{M} L(y^{(i)}, c)； \\ \qquad\; (2). 循环训练K个模型 k=1,2,\cdots,K \\ \qquad\qquad (a). 计算残差：对于i=1,2,\cdots,M \\ \qquad\qquad\qquad\qquad r_{ki} = -\left[ \frac{\partial L(y^{(i)}, \; f(x^{(i)}))} {\partial f(x^{(i)})} \right]_{f(x) = f_{k-1}(x)} \\ \qquad\qquad (b). 拟合残差r_{ki}学习一个回归树，得到第k颗树的叶结点区域R_{kj}，\quad j=1,2,\cdots,J \\ \qquad\qquad (c). 对j=1,2,\cdots,J, 计算：\\ \qquad\qquad\qquad\qquad c_{kj} = \arg \min_c \sum_{x^{(i)} \in R_{kj}} L(y^{(i)}, \; f_{k-1}(x^{(i)}) + c)\\ \qquad\qquad (d). 更新模型：\\ \qquad\qquad\qquad\qquad f_k(x) = f_{k-1}(x) + \sum_{j=1}^{J} c_{kj} I(x \in R_{kj}) \\ \qquad\; (3). 得到回归提升树 \\ \qquad\qquad\qquad \hat{f}(x) = f_K(x) = \sum_{k=1}^{K} \sum_{j=1}^{J} c_{kj} I(x \in R_{kj}) \\ \}$

使用scikit-learn中的GBDT

在scikit-learn中对GBDT算法有了很好的封装，对于分类可以选择的损失函数有逻辑回归和指数函数，对于回归的损失函数相对比较多，有最小二乘法、最小绝对偏差函数、huber以及分位数等。具体损失函数的描述可以参考下面的图片：

下面是sklearn中的一个分类原例：

>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> X, y = make_hastie_10_2(random_state=0)
>>> X_train, X_test = X[:2000], X[2000:]
>>> y_train, y_test = y[:2000], y[2000:]
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
...     max_depth=1, random_state=0).fit(X_train, y_train)
>>> clf.score(X_test, y_test)                 
0.913...

推荐GBDT树的深度：6
（横向比较：DecisionTree/RandomForest需要把树的深度调到15或更高）

GBDT与XGBOOST差别

XGBoost，在计算速度和准确率上，较GBDT有明显的提升。XGBoost的全称是eXtreme Gradient Boosting
1. 传统GBDT以CART作为基分类器，xgboost还支持线性分类器，这个时候xgboost相当于带L1和L2正则化项(可以看前面的博文)的Logistics回归（分类问题）或者线性回归（回归问题）。

传统GBDT在优化时只用到一阶导数信息，xgboost则对代价函数进行了二阶泰勒展开，同时用到了一阶和二阶导数。顺便提一下，xgboost工具支持自定义代价函数，只要函数可一阶和二阶求导。
Xgboost在代价函数里加入了正则项，用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出的score的L2模的平方和。从Bias-variance tradeoff角度来讲，正则项降低了模型的variance，使学习出来的模型更加简单，防止过拟合，这也是xgboost优于传统GBDT的一个特性。
Shrinkage（缩减），相当于学习速率（xgboost中的eta）。xgboost在进行完一次迭代后，会将叶子节点的权重乘上该系数，主要是为了削弱每棵树的影响，让后面有更大的学习空间。实际应用中，一般把eta设置得小一点，然后迭代次数设置得大一点。（补充：传统GBDT的实现也有学习速率）
列抽样（column subsampling）。xgboost借鉴了随机森林的做法，支持列抽样，不仅能降低过拟合，还能减少计算，这也是xgboost异于传统gbdt的一个特性。
缺失值的处理。对于特征的值有缺失的样本，xgboost可以自动学习出它的分裂方向。
xgboost工具支持并行。boosting不是一种串行的结构吗?怎么并行的？注意xgboost的并行不是tree粒度的并行，xgboost也是一次迭代完才能进行下一次迭代的（第t次迭代的代价函数里包含了前面t-1次迭代的预测值）。xgboost的并行是在特征粒度上的。我们知道，决策树的学习最耗时的一个步骤就是对特征的值进行排序（因为要确定最佳分割点），xgboost在训练之前，预先对数据进行了排序，然后保存为block结构，后面的迭代中重复地使用这个结构，大大减小计算量。这个block结构也使得并行成为了可能，在进行节点的分裂时，需要计算每个特征的增益，最终选增益最大的那个特征去做分裂，那么各个特征的增益计算就可以开多线程进行。
可并行的近似直方图算法。树节点在进行分裂时，我们需要计算每个特征的每个分割点对应的增益，即用贪心法枚举所有可能的分割点。当数据无法一次载入内存或者在分布式情况下，贪心算法效率就会变得很低，所以xgboost还提出了一种可并行的近似直方图算法，用于高效地生成候选的分割点。