Java与算法之(12) - 老鼠再闯迷宫(广度优先算法)

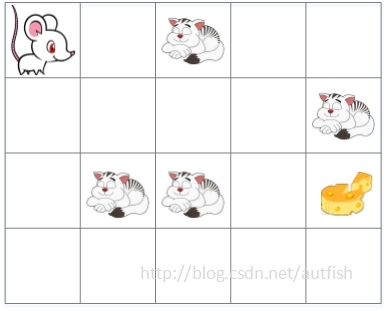
贪吃的小老鼠又回来了，这次有什么新的办法吃到奶酪呢？

规则不变，只能上下左右在格子内移动。

因为上次的深度优先算法让老鼠走了不少冤枉路，这次老鼠带来了帮手探路鼠。探路鼠的使用规则如下：

小老鼠按右、下、左、上的顺序向身边四个格子尝试放出探路鼠，如果遇到猫、出边界、已经有探路鼠存在的格子则放弃。

每只探路鼠都有唯一的顺序号，第一只从1开始，每放成功一只序号递增1。

老鼠探路完成后，找出当前未行动过的顺序号最小的探路鼠重复老鼠的工作，即尝试向右、下、左、上四个格子放出探路鼠。

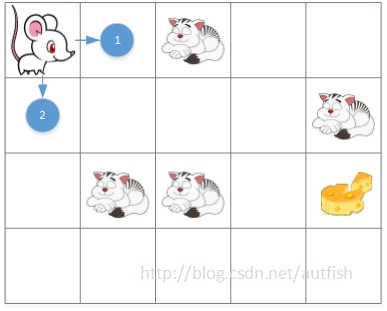
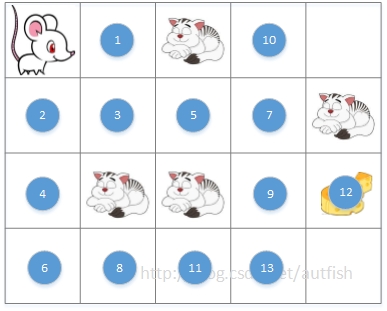
用图来解释一下，第一步，小老鼠放出两只探路鼠，如下：

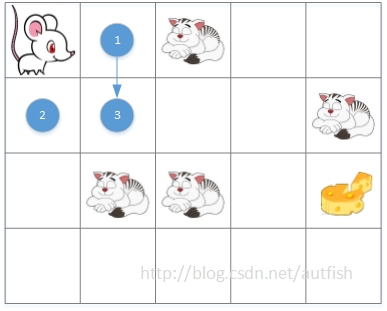
老鼠行动完成，按规则是1号探路鼠行动。由于地形所限，1号尝试了右、下、左、上四个方向后，只成功放出了3号。

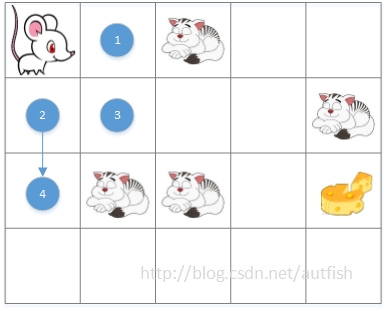
1号完成后，轮到2号行动，也只成功放出一只，即4号

据此规则不难推算出，接下来依次是：

3号放出5号

4号放出6号

5号放出7号

6号放出8号

7号放出9、10号

8号放出11号

9号放出12号

如下图：

注意12号探路鼠首先发现了奶酪，这时它向上一级即9号汇报，9号向7号汇报。。。，12->9->7->5->3->1->老鼠，可以计算出最少的步数是6。

上面的探路过程即广度优先搜索(Breadth First Search, BFS)，与深度优先搜索的一条路走到黑不同，每到一个新的位置都向四个方向分别探索，找出每一个分支，并对每一个分支继续探索。

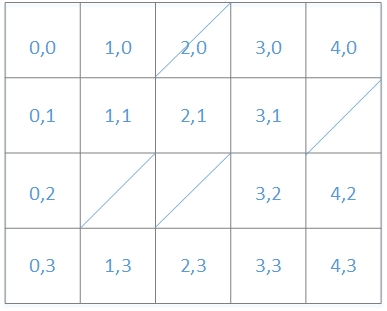
用程序来描绘这一过程，首先需要把迷宫“数字化“，如下图：

这样就可以用一个二维数组存储迷宫：

int width = 5;  //迷宫宽度
int height = 4;  //迷宫高度
	    
int[][] maze = new int[width][height];
	    
maze[2][0] = 1;
maze[1][2] = 1;
maze[2][2] = 1;
maze[4][1] = 1;

用一个同样大小的二维数组标记已经放了探路鼠的点

int[][] mark = new int[width][height];
mark[0][0] = 1;

每个“探路鼠”需要知道自己所在位置（坐标），自己的上一级是谁。为了方便，还用它记录了到达该位置需要的步数。用一个类来表示：

    static class Trace {

        public Trace(int x, int y, int father, int step) {
            this.x = x;
            this.y = y;
            this.father = father;
            this.step = step;
        }

        private int x;
        private int y;
        private int father;
        private int step;

        public int getX() {
            return x;
        }

        public void setX(int x) {
            this.x = x;
        }

        public int getY() {
            return y;
        }

        public void setY(int y) {
            this.y = y;
        }

        public int getFather() {
            return father;
        }

        public void setFather(int father) {
            this.father = father;
        }

        public int getStep() {
            return step;
        }

        public void setStep(int step) {
            this.step = step;
        }

        @Override
        public String toString() {
            return ToStringBuilder.reflectionToString(this, ToStringStyle.JSON_STYLE);
        }
    }

完整代码如下：

import org.apache.commons.lang3.builder.ToStringBuilder;
import org.apache.commons.lang3.builder.ToStringStyle;

import java.util.ArrayList;
import java.util.List;

/**
 * 老鼠走迷宫 BFS算法
 * Created by autfish on 2016/9/5.
 */
public class BfsRatMaze {

    int min = Integer.MAX_VALUE;
    int endX = 4;  //目标点横坐标
    int endY = 2;  //目标点纵坐标
    int width = 5;  //迷宫宽度
    int height = 4;  //迷宫高度
    int[][] maze;
    int[][] mark;

    static class Trace {

        public Trace(int x, int y, int father, int step) {
            this.x = x;
            this.y = y;
            this.father = father;
            this.step = step;
        }

        private int x;
        private int y;
        private int father;
        private int step;

        public int getX() {
            return x;
        }

        public void setX(int x) {
            this.x = x;
        }

        public int getY() {
            return y;
        }

        public void setY(int y) {
            this.y = y;
        }

        public int getFather() {
            return father;
        }

        public void setFather(int father) {
            this.father = father;
        }

        public int getStep() {
            return step;
        }

        public void setStep(int step) {
            this.step = step;
        }

        @Override
        public String toString() {
            return ToStringBuilder.reflectionToString(this, ToStringStyle.JSON_STYLE);
        }
    }

    public void bfs() {
        int[][] next = new int[][] { //按右->下->左->上的顺序尝试
                {1, 0},
                {0, 1},
                {-1, 0},
                {0, -1}
        };
        int head = 0, tail = 1;
        int startX = 0, startY = 0;
        int nextX, nextY;
        List<Trace> traces = new ArrayList<>();
        traces.add(head, new Trace(startX, startY, -1, 0));
        mark[startX][startY] = 1;
        int flag = 0;
        while(head < tail) {
            for(int k = 0; k <= 3; k++) {
                nextX = traces.get(head).getX() + next[k][0];
                nextY = traces.get(head).getY() + next[k][1];
                if(nextX < 0 || nextX >= width || nextY < 0 || nextY >= height) {  //超出边界
                    continue;
                }
                //没有障碍且没有探索过, 则把当前位置标记为未探索点
                if(maze[nextX][nextY] == 0 && mark[nextX][nextY] == 0) {
                    this.mark[nextX][nextY] = 1;
                    traces.add(tail, new Trace(nextX, nextY, head, traces.get(head).getStep() + 1));
                    tail++;
                }
                if(nextX == endX && nextY == endY) {
                    flag = 1;
                    break;
                }
            }
            if(flag == 1)
                break;
            //一个点的四个方向探索完成, 取编号最小的一个未探索点
            head++;
        }
        Trace end = traces.get(tail - 1);
        int father = end.getFather();
        System.out.println("共" + end.getStep() + "步");

        StringBuilder path = new StringBuilder();
        path.insert(0, "->[" + end.getX() + "," + end.getY() + "]");
        while(father >= 0) {
            Trace prev = traces.get(father);
            father = prev.getFather();
            if(father > -1)
                path.insert(0, "->[" + prev.getX() + "," + prev.getY() + "]");
            else
                path.insert(0, "[" + prev.getX() + "," + prev.getY() + "]");
        }
        System.out.println(path.toString());
    }

    public void initMaze() {
        this.maze = new int[width][height];
        this.mark = new int[width][height];

        this.maze[2][0] = 1;
        this.maze[1][2] = 1;
        this.maze[2][2] = 1;
        this.maze[4][1] = 1;
        this.mark[0][0] = 1;

        //打印迷宫 _表示可通行 *表示障碍 !表示目标
        for(int y = 0; y < height; y++) {
            for(int x = 0; x < width; x++) {
                if(x == endX && y == endY) {
                    System.out.print("!  ");
                }  else if(this.maze[x][y] == 1) {
                    System.out.print("*  ");
                } else {
                    System.out.print("_  ");
                }
            }
            System.out.println();
        }
        System.out.println();
    }

    public static void main(String[] args) {
        BfsRatMaze b = new BfsRatMaze();
        b.initMaze();
        b.bfs();
    }
}

运行结果：

_  _  *  _  _  
_  _  _  _  *  
_  *  *  _  !  
_  _  _  _  _  

共6步
[0,0]->[1,0]->[1,1]->[2,1]->[3,1]->[3,2]->[4,2]

用深度优先搜索的程序见：

Java与算法之(5) - 老鼠走迷宫(深度优先算法)