Mathematica绘制常见曲线

Mathematica绘制常见曲线

才疏学浅，资历欠佳，难免有误，望有心人批评指正。

border="0" width="350" height="100" src="http://music.163.com/outchain/player?type=2&id=412493245&auto=1&height=66">

本文主要用于展示自己使用mathematica绘制的数学上的常见和常用曲线（本来是动图的，只因技术不精，变成静图了）

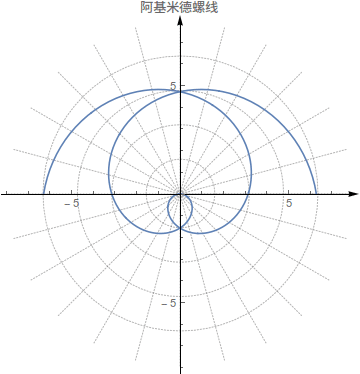
阿基米德螺线

Manipulate[
 PolarPlot[a t, {t, -2 \[Pi], 2 \[Pi]}, PlotTheme -> "Detailed",
  AxesStyle -> Arrowheads[{0, 0.03}], PlotLabel -> "阿基米德螺线",
  PlotLegends -> None], {a, -1, 1}]

Manipulate[
 PolarPlot[a Sin[3 t], {t, 0, Pi}, PlotTheme -> "Web",
  AxesStyle -> Arrowheads[{0, 0.03}]], {a, -1, 1}]

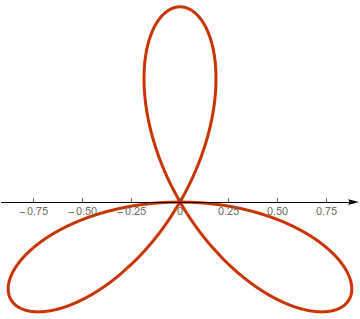
只是觉得好看，并非我所画

PolarPlot[
 Evaluate[Table[
   Abs[Sin[\[Theta] + i]], {i, 0, 2 Pi, 2 Pi/16}]], {\[Theta], 0,
  2 Pi}, PlotStyle -> Thick,
 ColorFunction -> Function[{x, y, t, r}, Hue[r]], Axes -> False,
 RegionFunction -> Function[{x, y, t, r}, r < 0.555],
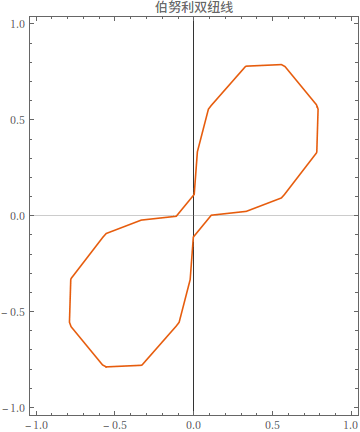
 ColorFunctionScaling -> False, PlotPoints -> 20, MaxRecursion -> 3]

伯努利双纽线

Manipulate[
 ContourPlot[(x^2 + y^2)^2 == 2 a^2 x y, {x, -1, 1}, {y, -1, 1},
  AspectRatio -> Full, PlotTheme -> "Scientific",
  PlotLabel -> "伯努利双纽线", AxesStyle -> Arrowheads[{0, 0.03}]], {a, -1,
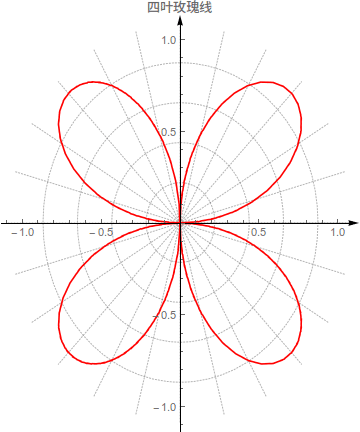
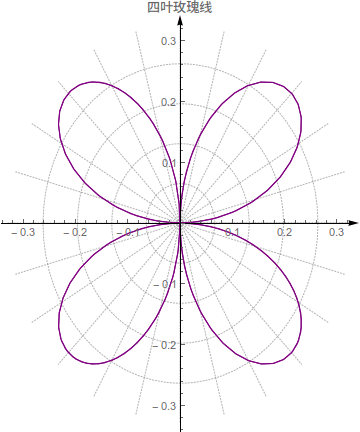
  1}]

四叶玫瑰线

Manipulate[
 PolarPlot[a Sin[2 t], {t, -2 Pi, 2 Pi}, PlotTheme -> "Detailed",
  AxesStyle -> Arrowheads[{0, 0.03}], AspectRatio -> Full,
  PlotStyle -> {Red, Dashed}, PlotLabel -> "四叶玫瑰线",
  PlotLegends -> Automatic], {a, -1, 1}]

Manipulate[
 PolarPlot[a Sin[2 t], {t, -2 Pi, 2 Pi}, PlotTheme -> "Detailed",
  AxesStyle -> Arrowheads[{0, 0.03}], AspectRatio -> Full,
  PlotStyle -> {Purple, Thickness[0.003]}, PlotLabel -> "四叶玫瑰线",
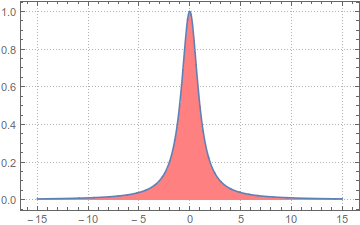
  PlotLegends -> Automatic], {a, -1, 1}]

做出图像并求解积分

Plot[1/(1 + x^2), {x, -15, 15}, PlotTheme -> "Detailed",
 PlotRange -> All, PlotRangePadding -> Scaled[.05], Filling -> Axis,
 FillingStyle -> {Opacity[0.7], Pink}]

Integrate[1/(1 + x^2), {x, -Infinity, Infinity}]

仅供学习参考与交流