概率论与数理统计(陈希孺)笔记2.2

2.2 随机向量

若随机变量$X_1,X_2,\cdots ,X_n$定义在同一个样本空间$\Omega$上, 则称$(X_1,X_2,\cdots ,$,$X_n$) 为一个$n$维随机向量或$n$维随机变量。

我们虽然可以仿照一维随机变量定义多维随机变量的分布函数,但分布函数在多维中意义不大,这里仅给出其定义.

$X=\left(X_1,\cdots ,X_n\right)$为一个$n$维随机向量, 对任意实数$x_1,\cdots ,x_n$, 称$n$元函数$F\left(x_1,\cdots ,x_n\right)=P\left(X_1⩽x_1,X_2⩽x_2,\cdots ,X_n⩽x_n\right)$为随机向量$X=\left(X_1,\cdots ,X_n\right)$的分布函数。

下面介绍连续性随机向量和连续型随机向量的分布.

2.2.1 离散型随机向量的分布

设$n$维随机向量$X=\left(X_1,\cdots ,X_n\right)$的每一个分量$X_i$都是一维离散型随机变量,$i=1,2,\cdots ,n$, 则称$X$为离散型的。若 { a i 1 , a i 2 , ⋯   } \left\{a_{i 1}, a_{i 2}, \cdots\right\} {ai1​,ai2​,⋯}为$X_i$的全部可能值, 则对$j_k=1,2,\cdots ,k=1,2,\cdots ,n$, 概率
$$p\left(j_1,j_2,\cdots ,j_n\right)=P\left(X_1=a_{1j_1},X_2=a_{2j_2},\cdots ,X_n=a_{n{j}_n}\right)$$
称为随机向量$X=\left(X_1,\cdots ,X_n\right)$的概率函数或概率分布率。

多项分布

多项分布式最重要的离散型多维分布,其定义如下:

设$A_1,A_2,\cdots ,A_n$是 某一试验之下的完备事件群.现在将试验独立地重复$N$次, 而以$X_i$记在这$N$次试验中事 件$A_i$出现的次数,$i=1,\cdots ,n$, 则$X=\left(X_1,\cdots ,X_n\right)$的概率分布为多项分布,记为$M\left(N;p_1,\cdots ,p_n\right)$.

易得其公式为

$$P\left(X_1=k_1,X_2=k_2,\cdots ,X_n=k_n\right)=\frac{N!}{k_1!k_2!\cdots k_n!}{p}_1^k{p}_2^k\cdots p_{n^n}^{k_n}$$

该公式直观理解就是将$N$个相异物体分成$n$堆, 各堆依次有$k_1,k_2,\cdots ,k_n$件,每件物品有$p_i$的概率分到第$i$堆.

2.2.2 连续型随机向量的分布

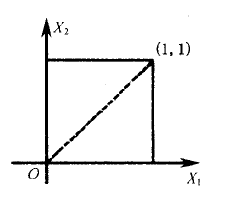
与离散型随机向量的定义不 同, 连续型随机向量不能简单地定义为 “其各分量都是一维连续型随机变量的 那种随机向量”.举一个例子:设$X_1\sim$$R(0,1),X_2=X_1$, 则 随 机 向量$\left(X_1,X_2\right)$的两个分量$X_1,X_2$都是连续型的.但$(X_1,X_2)$只能在单位正方形的对角线上取值,其概率之和必然为0.故不是连续型随机向量.

连续型随机向量的定义如下:

设$X=\left(X_1,\cdots ,X_n\right)$是一个$n$维随机向量.其取值可视为$n$维欧氏空间$R^n$中的一个点. 如果$X$的全部取值能充满$R^n$中某一区域,则称它是连续型的.

若$f\left(x_1,\cdots ,x_n\right)$是定义在$R^n$上的非负函数,使对$R^n$中的任何集合$A$, 有
$$P(X\in A)={\int }_A\cdots \int f\left(x_1,\cdots ,x_n\right)\mathrm{d}{x}_1\cdots \mathrm{d}{x}_n$$
则称$f$是$X$的(概率)密度函数,反应了$X$落在某点$\left(x_1,\cdots ,x_n\right)$的概率大小.

二维正态分布

二维正态分布的概率密度函数如下.该分布记为$N\left(a,b,{\sigma }_1^2,{\sigma }_2^2,\rho \right)$

$$\begin{array}{rl}p(x,y)=& \frac{1}{2\pi {\sigma }_1{\sigma }_2\sqrt{1-{\rho }^2}}\exp \{-\frac{1}{2\left(1-{\rho }^2\right)}[{\left(\frac{x-{\mu }_1}{{\sigma }_1}\right)}^2\\ & -2\rho \left(\frac{x-{\mu }_1}{{\sigma }_1}\right)\left(\frac{y-{\mu }_2}{{\sigma }_2}\right)+{\left(\frac{y-{\mu }_2}{{\sigma }_2}\right)}^2]\}\end{array}$$

二维正态分布的一个例子为一群人身高和体重的联合分布.

2.2.3 边缘分布

边缘分布说白了就是求随机向量某个分量的分布.

其公式为

$$离散型:P\left(X_1=a_{1k}\right)=\sum _{j_2,\cdots ,j_n}p\left(k,j_2,\cdots ,j_n\right),k=1,2,\cdots$$

$$连续型:f_1\left(x_1\right)={\int }_{-\infty }^{\infty }\cdots {\int }_{-\infty }^{\infty }f\left(x_1,x_2,\cdots ,x_n\right)\mathrm{d}{x}_2\cdots \mathrm{d}{x}_n$$

这些公式也可以看作是全概率公式.

例如,对于离散情况,要求$P(X_1=a_{1k})$.可以将事件A记为 { X 1 = a 1 k } \{X_1=a_{1k}\} {X1​=a1k​},将事件$B_i$记为 { X 2 = j 2 , ⋯   , X n = j n } \{X_2=j_2,\cdots,X_n=j_n\} {X2​=j2​,⋯,Xn​=jn​},穷尽$j_2,\cdots ,j_n$的所有取值情况,求该情况下事件$A$发生的条件概率$p\left(k,j_2,\cdots ,j_n\right)$,再累加起来记为事件A发生的概率.
$$\begin{array}{rl}P(A)& =P\left(B_1\right)P\left(A\mid B_1\right)+P\left(B_2\right)P\left(A\mid B_2\right)+\cdots \\ & =\sum _{j_2,\cdots ,j_n}p\left(k,j_2,\cdots ,j_n\right)\end{array}$$
下面给出离散型和连续型的例子.

多项分布的边缘分布

设$X=\left(X_1,\cdots ,X_n\right)$服从多项分布$M(N;p_1,\cdots ,$,$p_n$), 要求其边缘分布. 例如,考虑$X_1$, 我们把事件$A_1$作为一方,$A_2+\cdots +A_n$作为一方(它就是${\bar{A}}_1)$, 那么,$X_1$就 是在$N$次独立试验中,事件$A_1$发生的次数,而在每次试验中$A_1$发生的概率保持为$p_1$, 经过这一分析, 不待计算就可以明了:$X_1$的分布就是二项分布$B\left(N,p_1\right)$.

陈希孺在书中给出了详细的代数方法的证明过程,但正如陈希孺所说,学学概统更重要的式要形成概率思维,分析各种公式的概率意义和直观意义.所以这里不给出证明.

二维正态分布的边缘分布

若$\left(X_1,X_2\right)$有二维正态分布$N\left(a,b,{\sigma }_2^1,{\sigma }_2^2,\rho \right)$, 则$X_1$,$X_2$的边缘分布分别是一维正态分布$N\left(a,{\sigma }_1^2\right)$和$N\left(b,{\sigma }_2^2\right)$.

二维正态分布揭示了一个有趣的事实:一个随机向量$X=$$\left(X_1,\cdots ,X_n\right)$的分布$F$足以决定其任一分量$X_i$的$($边缘)分布$F_i$, 但反过来不对: 即使知道了所有$X_i$的边缘分布$F_i,i=1,\cdots ,n$, 也足以决定$X$的分布$F$.因为同样的$N\left(a,{\sigma }_1^2\right)$和$N\left(b,{\sigma }_2^2\right)$,有不同的$\rho$取值.

这个现象的解释是:边 缘分布只分别考虑了单个变量$X_i$的情况,而末涉及它们之间的 关系,而这个信息却是包含在$\left(X_1,\cdots ,X_{.}\right)$的分布之内的,.在二维正态分布中,$\rho$这个参数正好刻画 了两分量$X_1$和$X_2$之间的关系.

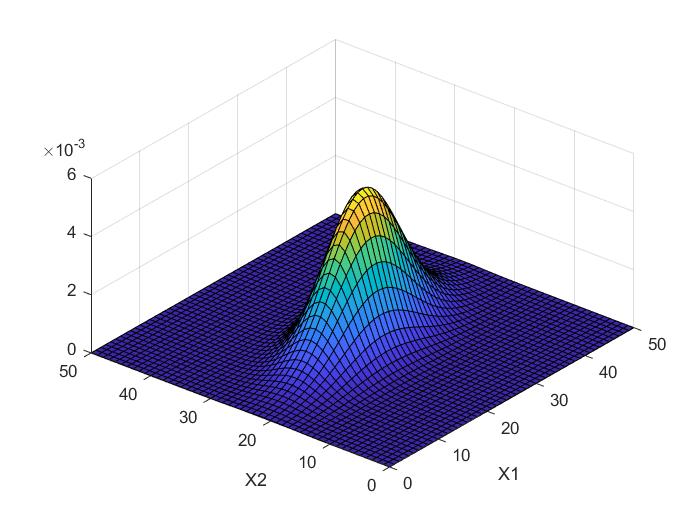
例如,我们用matlab作图,考察$N\left(25,16\right)$和$N\left(25,64\right)$在不同$\rho$下的概率密度.下面三张图展示了$\rho =0,0.5,-0.5$时对应的概率密度.同时我们可以看到,$N\left(a,b,{\sigma }_2^1,{\sigma }_2^2,\rho \right)$的概率密度函数在$XOY$平面的投影是一个椭圆.