概率论与数理统计（陈希孺）学习笔记

由于平常学习自然语言处理的很多算法都来源于概率论和数理统计，因此找来陈老先生的著作温习巩固一下。具体内容请参考原著，本文仅作个人学习记录。

1.基本概念

主观概率：可以理解为一个人针对某一事件的一种心态或倾向性。这种倾向性一是根据其经验和知识所得，还有可能是根据其自身利害关系所得。主观概率虽然不具有坚实的客观理由基础，但是它却广泛存在于我们的生活当中，并可能反映认识主体的一种倾向性，因而具有其社会意义。

事件：概率论中的事件不是指已经发生了的情况，而是指某种（或某些）情况的‘陈述’，它可能发生，也可能不发生，发生与否，要到有关的‘试验’有了结果以后才能知道。事件特征有三（1）有一个明确界定的试验；（2）在试验前就明确了这个试验的全部可能结果；（3）当有一个明确的陈述界定了试验结果的全部可能结果中的一个确定的部分，其就叫做一个事件。由于事件是否在某次试验中的发生取决于机遇，因此在概率论中，事件常称为“随机事件”，其极端情况为“必然事件”和“不可能事件”。

古典概率定义：设一个试验有N个等可能结果，而事件E恰包含其中M个结果，则事件E的概率，记为P(E)=M/N。古典概率只能用于全部试验结果为有限个且等可能性成立的情况。如果引申为试验结果有无限多个的情况，就是“几何概率”，即等面积，等概率。

频率与概率：频率只是概率的估计而非概率本身，但当试验重复次数无限增大时，我们认为此时频率的极限就是概率。（大数定理）

排列与组合：排列有次序，而组合没有。

（1）排列公式：n个相异物体取r（1<=r<=n）个的不同排列总数

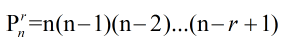
当n=r时，P=r(r-1)...1=r!，其中 0！=1

（2）组合公式：n个相异物件取r（1<=r<=n）个的不同组合总数。因为每一个包含r个物件的组合都可以产生r！个不同的排列，因此排列数应该是组合数的r！倍。

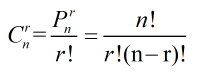
条件概率定义：设有两个事件A,B，且P（B）！=0，则“在给定B发生的条件下A的条件概率”，记为P（A|B）=P(AB)/P(B)

证明过程：设一个试验有N个等可能的结果，事件A、B分别包括其中M1和M2个结果，他们有M12个公共结果，即事件AB所包含的结果。若已经给定B发生，则可能的结果由N个缩减到M2个，其中只有M12个结果使事件A发生，则此时

P(A|B)=M12/M2=(M12/N)/(M2/N)=P(AB)/P(B)

事件的独立性：两个事件A、B，A的无条件概率P(A)与其给定条件B发生下的条件概率P(A|B)之间存在一些关联。若P(A|B)>P(A)，则B发生使A发生的可能性增大了；若P(A|B)=P(A)，则B发生与否对A发生的可能性毫无影响，此时就称A,B两事件独立。结合条件概率公式P(A|B)=P(AB)/P(B)可得，P(AB)=P(A)P(B)。

定理：若干个独立事件A1,...,An之积的概率等于各事件概率的乘积：P(A1...An)=P(A1)..P(An)

相加是互斥，相乘是独立！

全概率公式：设B1,B2...为有限或无限个事件，他们两两互斥且在每次试验中至少发生一个，即：

&#