阅读材料:Ramsay, J.O., Silverman, B.W. (2005) Functional Data Analysis (2nd Edition) Section 4.1, 4.2, 4.3, 4.4, 4.5, 5.1, 5.2, 5.3, 5.4 and 5.5.
Contents
1 Fitting and smoothing
1.1 Fitted by least squares
For a single curve
y i = x ( t i ) + ϵ , y_i = x(t_i) + \epsilon, yi=x(ti)+ϵ,
we want to estimate
x ( t ) ≈ ∑ j = 1 k c j ϕ j ( t ) . x(t) \approx \sum_{j=1}^k c_j \phi_j (t). x(t)≈j=1∑kcjϕj(t).
Minimize the sum of squared errors:
S S E = ∑ i = 1 n ( y i − x ( t i ) ) 2 = ∑ i = 1 n ( y i − c T Φ ( t i ) ) 2 , SSE = \sum_{i=1}^n (y_i - x(t_i))^2 = \sum_{i=1}^n (y_i - \mathbf{c}^T \Phi (t_i))^2, SSE=i=1∑n(yi−x(ti))2=i=1∑n(yi−cTΦ(ti))2,
where
c k × 1 = ( c 1 , c 2 , . . . , c j , . . . , c k ) T , \mathbf{c}_{k \times1} = (c_1, c_2, ..., c_j, ..., c_k)^T, ck×1=(c1,c2,...,cj,...,ck)T,
Φ k × 1 ( t i ) = ( ϕ 1 ( t i ) , ϕ 2 ( t i ) , . . . , ϕ j ( t i ) , . . . , ϕ k ( t i ) ) T . \Phi_{k \times 1}(t_i) = \big( \phi_1(t_i), \phi_2(t_i), ..., \phi_j(t_i), ..., \phi_k(t_i) \big)^T. Φk×1(ti)=(ϕ1(ti),ϕ2(ti),...,ϕj(ti),...,ϕk(ti))T.
Denote
y n × 1 = ( y 1 , y 2 , . . . , y i , . . . , y n ) T , \mathbf{y}_{n \times 1} = (y_1, y_2, ..., y_i, ..., y_n)^T, yn×1=(y1,y2,...,yi,...,yn)T,
Φ n × k = ( Φ ( t 1 ) , Φ ( t 2 ) , … , Φ ( t i ) , … , Φ ( t n ) ) = ( ϕ 1 ( t 1 ) , ϕ 1 ( t 2 ) , … , ϕ 1 ( t i ) , … , ϕ 1 ( t n ) ϕ 2 ( t 1 ) , ϕ 2 ( t 2 ) , … , ϕ 2 ( t i ) , … , ϕ 2 ( t n ) ⋮ ⋮ ⋮ ⋮ ϕ j ( t 1 ) , ϕ j ( t 2 ) , … , ϕ j ( t i ) , … , ϕ j ( t n ) ⋮ ⋮ ⋮ ⋮ ϕ k ( t 1 ) , ϕ k ( t 2 ) , … , ϕ k ( t i ) , … , ϕ k ( t n ) ) . \begin{aligned} \mathbf{\Phi}_{n \times k} &= ~~ \left( \begin{array}{ccc} ~ \Phi(t_1), & ~ \Phi(t_2), & \ldots, ~ & \Phi(t_i), & \ldots, ~ & \Phi(t_n) ~ \\ \end{array} \right) \\ {} \\ &= \left( \begin{array}{ccc} \phi_1(t_1), & \phi_1(t_2), & \ldots, & \phi_1(t_i), & \ldots, & \phi_1(t_n) \\ \phi_2(t_1), & \phi_2(t_2), & \ldots, & \phi_2(t_i), & \ldots, & \phi_2(t_n) \\ \vdots & \vdots & & \vdots & & \vdots\\ \phi_j(t_1), & \phi_j(t_2), & \ldots, & \phi_j(t_i), & \ldots, & \phi_j(t_n) \\ \vdots & \vdots & & \vdots & & \vdots\\ \phi_k(t_1), & \phi_k(t_2), & \ldots, & \phi_k(t_i), & \ldots, & \phi_k(t_n) \\ \end{array} \right) \end{aligned}. Φn×k= ( Φ(t1), Φ(t2),…, Φ(ti),…, Φ(tn) )=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎛ϕ1(t1),ϕ2(t1),⋮ϕj(t1),⋮ϕk(t1),ϕ1(t2),ϕ2(t2),⋮ϕj(t2),⋮ϕk(t2),…,…,…,…,ϕ1(ti),ϕ2(ti),⋮ϕj(ti),⋮ϕk(ti),…,…,…,…,ϕ1(tn)ϕ2(tn)⋮ϕj(tn)⋮ϕk(tn)⎠⎟⎟⎟⎟⎟⎟⎟⎟⎞.
Then we can write
S S E ( c ) = ( y − Φ c ) T ( y − Φ c ) . SSE(\mathbf{c}) = (\mathbf{y} - \mathbf{\Phi c})^T (\mathbf{y} - \mathbf{\Phi c}). SSE(c)=(y−Φc)T(y−Φc).
The ordinary least squares estimate is
c ^ = a r g m i n ( y − Φ c ) T ( y − Φ c ) = ( Φ T Φ ) − 1 Φ T y . \begin{aligned} \hat{\mathbf{c}} &= argmin (\mathbf{y} - \mathbf{\Phi c})^T (\mathbf{y} - \mathbf{\Phi c}) \\ &= (\mathbf{\Phi}^T \mathbf{\Phi})^{-1} \mathbf{\Phi}^T \mathbf{y} \end{aligned}. c^=argmin(y−Φc)T(y−Φc)=(ΦTΦ)−1ΦTy.
Then we have the estimate
x ^ ( t ) = Φ 1 × k ( t ) ⋅ c ^ = Φ ( t ) ⋅ ( Φ T Φ ) − 1 Φ T y ⏞ k × 1 . \hat{x}(t) = \Phi_{1 \times k} (t) \cdot \hat{\mathbf{c}} = \Phi (t) \cdot \overbrace{(\mathbf{\Phi}^T \mathbf{\Phi})^{-1} \mathbf{\Phi}^T \mathbf{y}}^{k \times 1}. x^(t)=Φ1×k(t)⋅c^=Φ(t)⋅(ΦTΦ)−1ΦTy k×1.
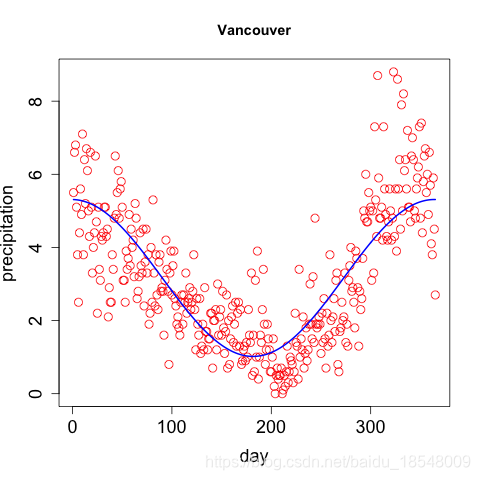
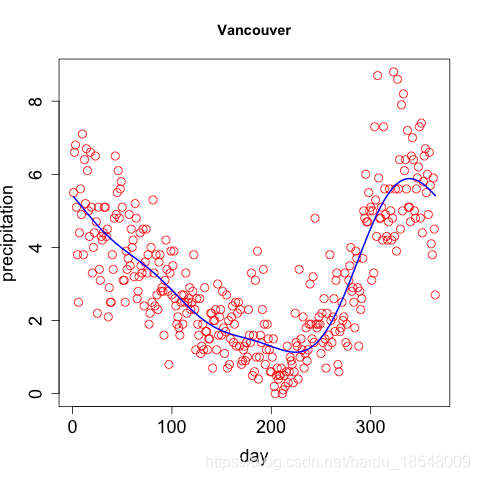
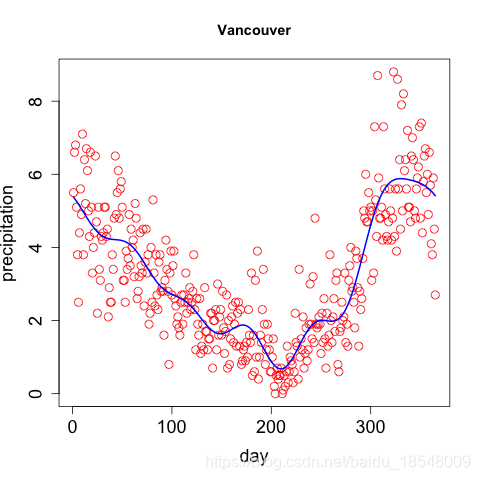
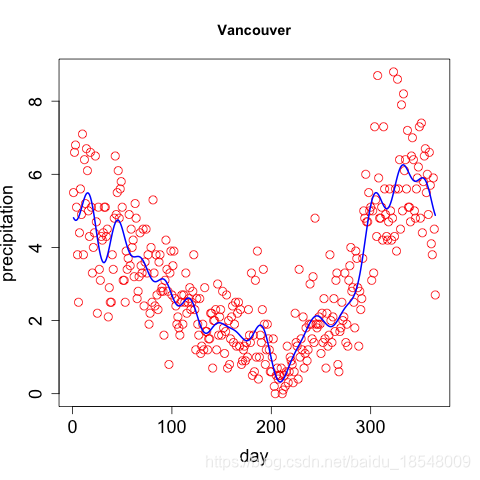
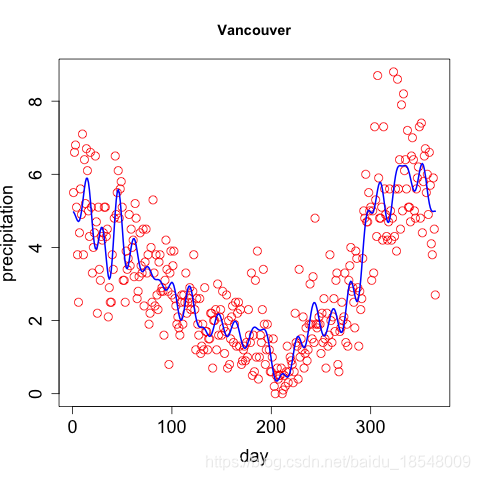
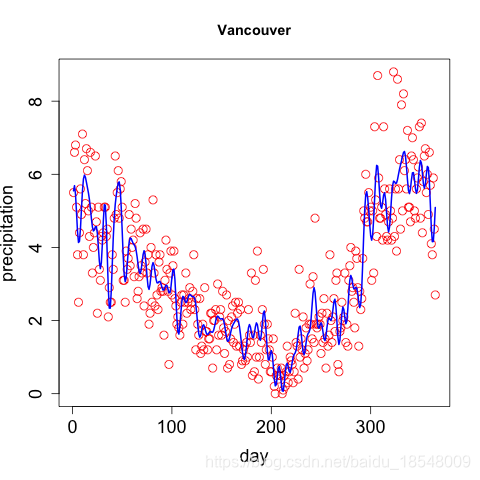
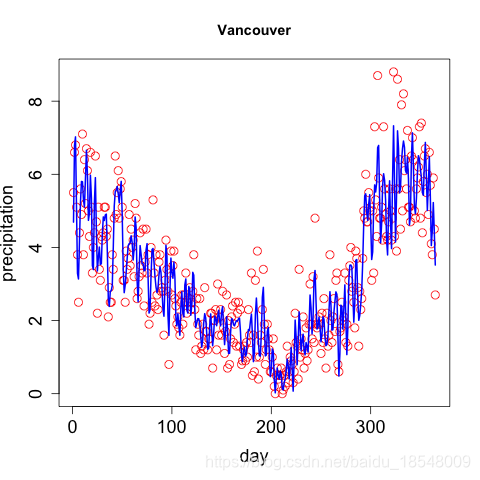
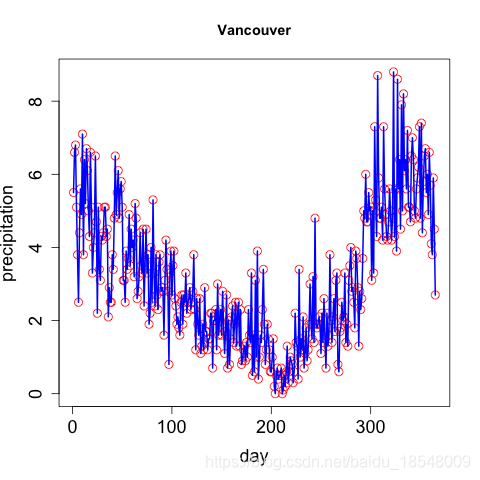
1.2 Choosing the number of basis functions
- Trade off:
fails to capture interesting features of the curves ↔ i . e . k t h e n u m b e r o f b a s i s f u n c t i o n s \xleftrightarrow[i.e. ~ k]{the ~ number ~ of ~ basis ~ functions} the number of basis functions i.e. k more flexible but “overfit”, reflect errors of measurement - Spline basis: number of knots ↗ \nearrow ↗ , the order of the basis ↗ \nearrow ↗ ⟹ \Longrightarrow ⟹ more flexible
|
| |||
|
|
|
|
|
|
|
|
This trade-off can be express in terms of
- the bias of the estimate of
x
(
t
)
x(t)
x(t):
B i a s [ x ^ ( t ) ] = x ( t ) − E [ x ^ ( t ) ] , Bias[\hat{x}(t)] = x(t) - E[\hat{x}(t)], Bias[x^(t)]=x(t)−E[x^(t)], - the sampling variance of the estimate:
V a r [ x ^ ( t ) ] = E [ { x ( t ) − E [ x ^ ( t ) ] } 2 ] . Var[\hat{x}(t)] = E \big[ \{ x(t) - E[\hat{x}(t)] \}^2 \big]. Var[x^(t)]=E[{x(t)−E[x^(t)]}2].
| small bias but large sampling variance | ↔ i . e . k t h e n u m b e r o f b a s i s f u n c t i o n s \xleftrightarrow[i.e. ~ k]{the ~ number ~ of ~ basis ~ functions} the number of basis functions i.e. k | small sampling variance but large bias |
|---|
Usually, we would really like to minimize mean squared error
M S E [ x ^ ( x ) ] = E [ { x ^ ( t ) − x ( t ) } 2 ] . MSE[\hat{x} (x)] = E\big[ \{ \hat{x}(t) - x(t) \}^2 \big]. MSE[x^(x)]=E[{x^(t)−x(t)}2].
There is a simple relationship between MSE and bias/variance
M
S
E
[
x
^
(
t
)
]
=
B
i
a
s
2
[
x
^
(
t
)
]
+
V
a
r
[
x
^
(
t
)
]
,
MSE[\hat{x} (t)] = Bias^2[\hat{x}(t)] + Var[\hat{x}(t)],
MSE[x^(t)]=Bias2[x^(t)]+Var[x^(t)],
for each value of
t
t
t.
In general, we would like to minimize the integrated mean squared error:
I M S E [ x ^ ( t ) ] = ∫ M S E [ x ^ ( t ) ] d t . IMSE[\hat{x} (t)] = \int MSE[\hat{x} (t)] ~ dt. IMSE[x^(t)]=∫MSE[x^(t)] dt.
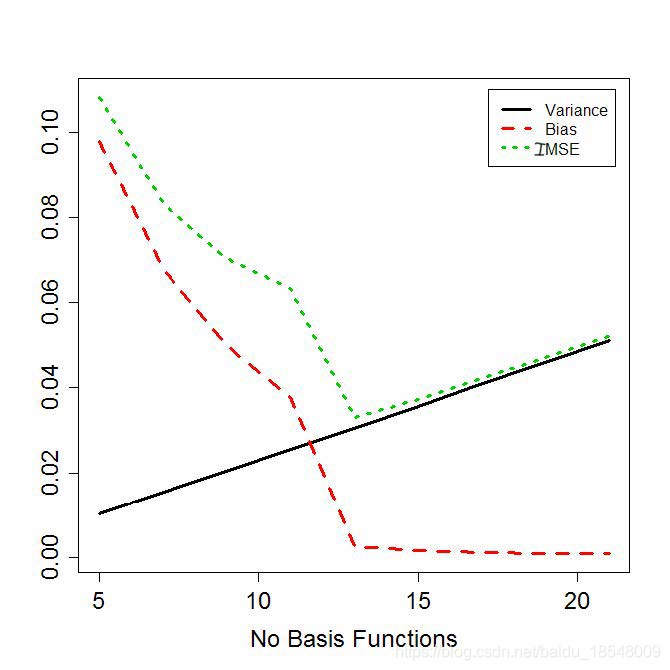
Eg. Bias and variance against
k
k
k from simulation.
1.3 Cross-validation
One method of choosing a model is through cross validation.
- leave out one observation ( t i , y i ) (t_i, y_i) (ti,yi);
- estimate x ^ − i ( t ) \hat{x}_{-i}(t) x^−i(t) from remaining data;
- measure the model’s performance in predicting t i t_i ti. i.e. y i − x ^ − i ( t i ) y_i - \hat{x}_{-i}(t_i) yi−x^−i(ti);
- choose
k
k
k to minimize the ordinary cross-validation score:
O C V [ x ^ ] = ∑ ( y i − x ^ − i ( t i ) ) 2 , OCV[\hat{x}] = \sum \big(y_i - \hat{x}_{-i}(t_i) \big)^2, OCV[x^]=∑(yi−x^−i(ti))2,
for a linear smooth y ^ = S y \hat{y} = Sy y^=Sy
O C V [ x ^ ] = ∑ ( y i − x ^ i ( t i ) ) 2 ( 1 − s i i ) 2 . OCV[\hat{x}] = \sum \frac{\big(y_i - \hat{x}_{i}(t_i) \big)^2}{(1 - s_{ii})^2}. OCV[x^]=∑(1−sii)2(yi−x^i(ti))2.
1.4 Summary
- Fitting smooth curves is just linear regression using basis functions as independent variables.
- Trade-off between bias and variance in choosing the number of basis functions k k k.
- Cross-validation is one way to quantitatively find the best number of basis functions.
- Confidence intervals can be calculated using the standard model, but these should be treated with care.
2 Roughness penalty
Some disadvantages of basis expansions:
- Discrete choice of number of basis functions ⇒ \Rightarrow ⇒ additional variability;
- Non-hierarchical bases (eg. B-splines) make life more complicated;
- Not necessarily easy to tailor to problems at hand.
2.1 Smoothing penalties
Add a penalty to the least-squares criterion:
P E N S S E λ ( x ) = S S E + λ J [ x ] = [ y − x ( t ) ] [ y − x ( t ) ] T + λ J [ x ] , \begin{aligned} PENSSE_\lambda (x) &= SSE + \lambda J[x] \\ &= [\mathbf{y} - x(\mathbf{t})][\mathbf{y} - x(\mathbf{t})]^T + \lambda J[x], \\ \end{aligned} PENSSEλ(x)=SSE+λJ[x]=[y−x(t)][y−x(t)]T+λJ[x],
where
- J [ x ] J[x] J[x] measures “roughness” of x x x;
-
λ
\lambda
λ is a smoothing parameter measuring compromise between fit and smoothness.
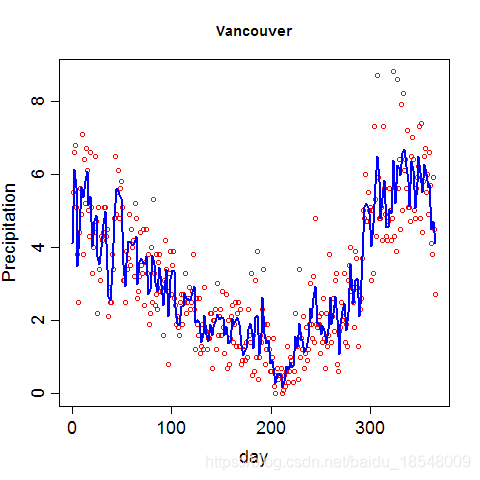
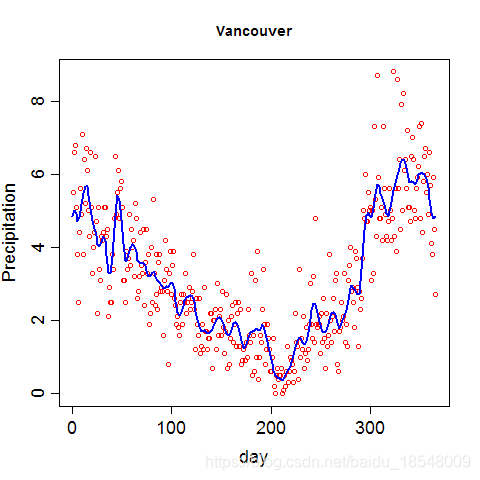
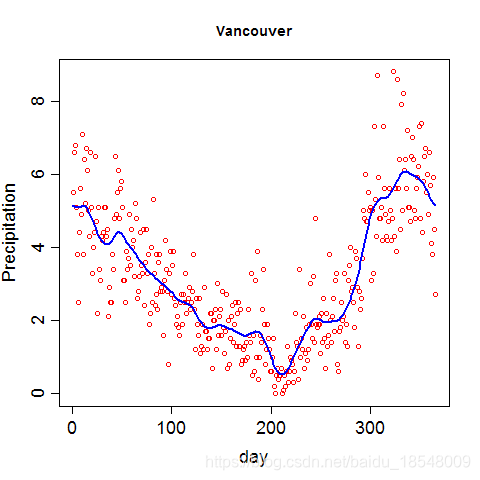
- λ → ∞ ⇒ \lambda \rightarrow \infty \Rightarrow λ→∞⇒ roughness increase penalty, x ( t ) x(t) x(t) becomes smooth.
- λ → 0 ⇒ \lambda \rightarrow 0 \Rightarrow λ→0⇒ penalty reduces, x ( t ) x(t) x(t) fits data better.
|
| ||
|
|
|
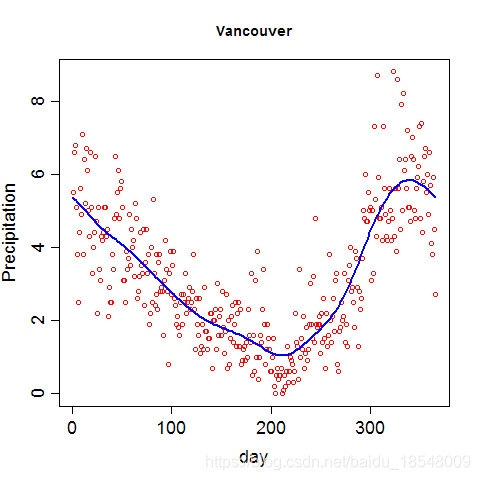
|
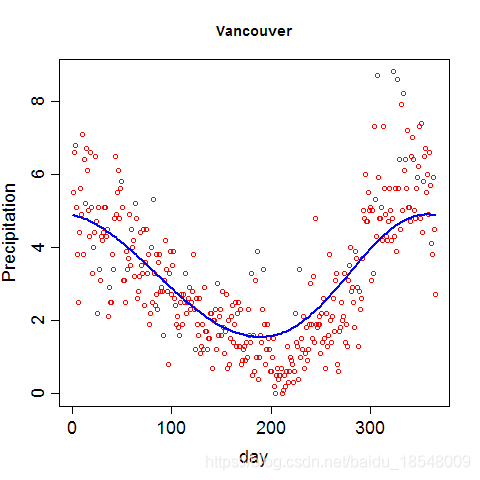
|
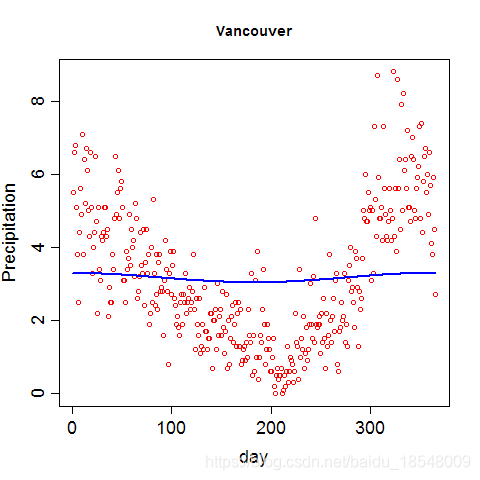
|
2.2 The D D D operator
To increase smoothness is to eliminate small “wiggles” in the data.
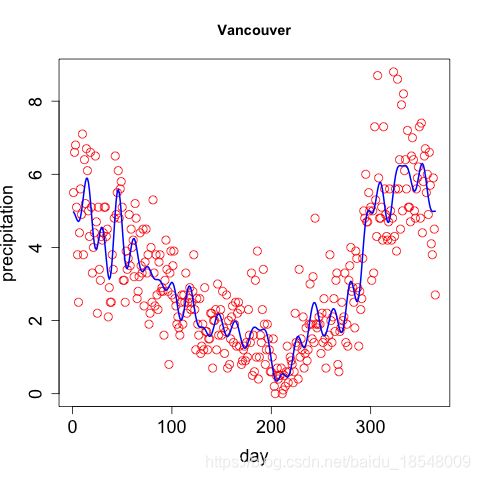
For a function x ( t ) x(t) x(t), denote
D
x
(
t
)
=
d
d
t
x
(
t
)
.
Dx(t) = \frac{d}{dt} x(t).
Dx(t)=dtdx(t).
Further derivatives in terms of powers of
D
D
D is denoted by
D
2
x
(
t
)
=
d
2
d
t
2
x
(
t
)
,
.
.
.
,
D
k
x
(
t
)
=
d
k
d
t
k
x
(
t
)
,
.
.
.
\begin{aligned} D^2x(t) &= \frac{d^2}{dt^2} x(t), \\\\ &..., \\\\ D^kx(t) &= \frac{d^k}{dt^k} x(t), \\\\ &... \end{aligned}
D2x(t)Dkx(t)=dt2d2x(t),...,=dtkdkx(t),...
-
D
x
(
t
)
Dx(t)
Dx(t) is the instantaneous slope of
x
(
t
)
x(t)
x(t);
D 2 x ( t ) D^2x(t) D2x(t) is its curvature. - We measure the size of the curvature for all of
f
f
f by
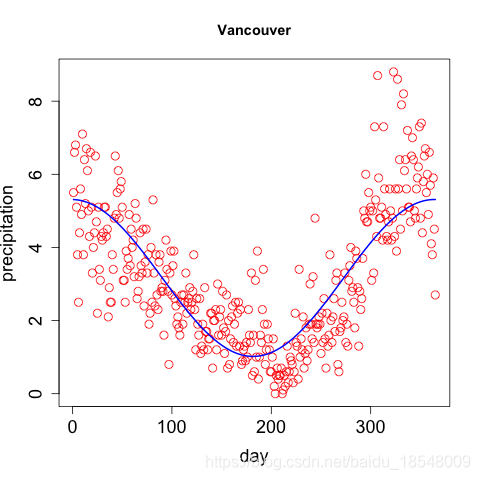
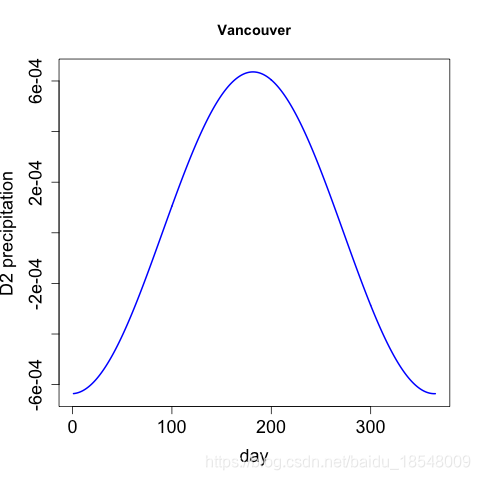
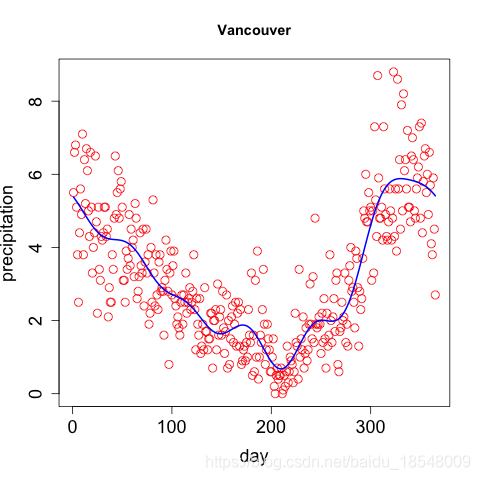
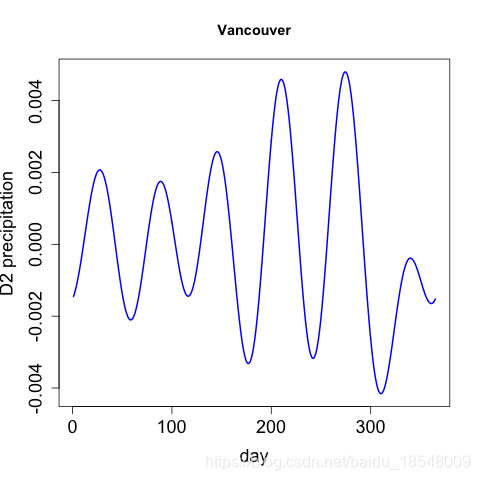
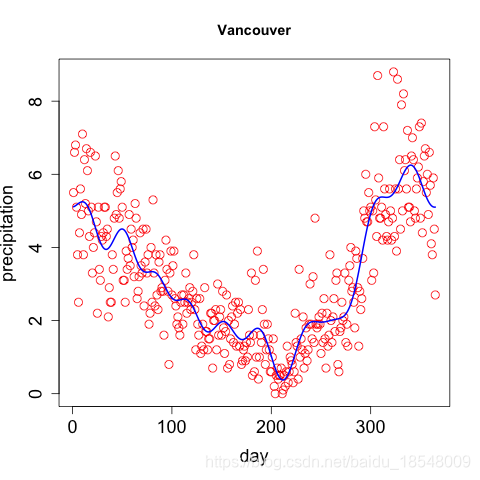
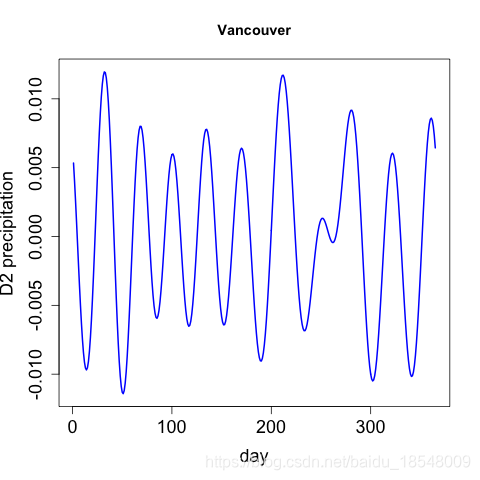
J 2 ( x ) = ∫ [ D 2 x ( t ) ] 2 d t . J_2(x) = \int \big[ D^2x(t) \big]^2 dt. J2(x)=∫[D2x(t)]2dt.
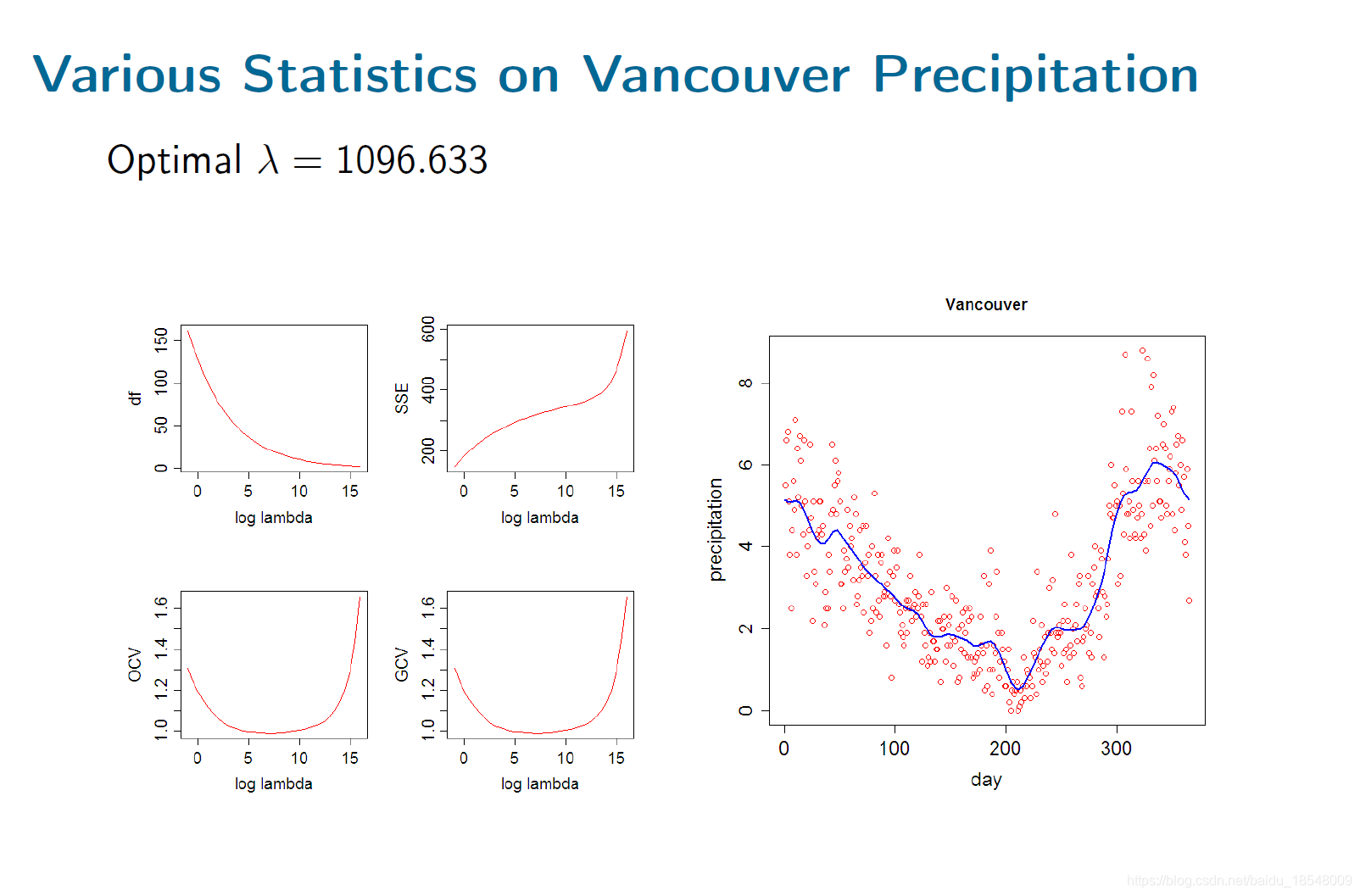
Eg. Curvature of vancouver precipitation
|
| |
|
|
|
| |
|
|
|
| |
|
|
2.3 The roughness of derivatives
Sometimes we may want to examine a derivative of x ( t ) x(t) x(t), say D 2 x ( t ) D^2x(t) D2x(t).
We then should consider the roughness of that derivative
D 2 [ D 2 x ( t ) ] = D 4 x ( t ) . D^2 \big[ D^2 x(t) \big] = D^4 x(t). D2[D2x(t)]=D4x(t).
This means we measure
J 4 [ x ] = ∫ [ D 4 x ( t ) ] 2 d t . J_4[x] = \int \big[ D^4 x(t) \big]^2 dt. J4[x]=∫[D4x(t)]2dt.
And the roughness of the mth derivative is
J m + 2 [ x ] = ∫ [ D m + 2 x ( t ) ] 2 d t . J_{m+2}[x] = \int \big[ D^{m+2} x(t) \big]^2 dt. Jm+2[x]=∫[Dm+2x(t)]2dt.
2.4 The smoothing spline theorem
Consider the “usual” penalized squared error:
P E N S S E λ ( x ) = [ y − x ( t ) ] T [ y − x ( t ) ] + λ ∫ [ D 2 x ( t ) ] 2 d t . PENSSE_\lambda (x) = [\mathbf{y} - x(\mathbf{t})]^T [\mathbf{y} - x(\mathbf{t})] + \lambda \int [D^2 x(t)]^2 dt. PENSSEλ(x)=[y−x(t)]T[y−x(t)]+λ∫[D2x(t)]2dt.
A remarkable theorem tells us that the function x ( t ) x(t) x(t) that minimizes P E N S S E λ ( x ) PENSSE_\lambda(x) PENSSEλ(x) is
- a spline function of order 4 (piecewise cubic),
- with a knot at each sample point t j t_j tj.
This is often referred to simply as cubic spline smoothing.
As x ( t ) x(t) x(t) is of the form
x ( t ) = Φ ( t ) T c , x(t) = \Phi (t)^T \mathbf{c}, x(t)=Φ(t)Tc,
where Φ ( t ) \Phi(t) Φ(t) is a 1 × k 1 \times k 1×k vector of B-spline basis functions.
The number of basis function (i.e. k k k) is the sum of order ( m m m) and the number of interior knots:
k = 4 + ( n − 2 ) = n + 2. k = 4 + (n - 2) = n + 2. k=4+(n−2)=n+2.
Then we need to calculate c c c.
2.4.1 Calculating the penalized fit
When x ( t ) = Φ ( t ) T c x(t) = \Phi (t)^T \mathbf{c} x(t)=Φ(t)Tc, we have that
∫ [ D m x ( t ) ] 2 d t = ∫ D m [ Φ ( t ) T c ] T [ Φ ( t ) T c ] d t = ∫ c T D m Φ ( t ) D m Φ ( t ) T c d t = c T R c . \begin{aligned} \int \big[ D^m x(t) \big]^2 ~ dt &= \int D^m \big[ \Phi (t)^T \mathbf{c} \big]^T \big[ \Phi (t)^T \mathbf{c} \big] ~ dt \\\\ &= \int \mathbf{c}^T D^m \Phi (t) D^m \Phi (t)^T \mathbf{c} ~ dt \\\\ &= \mathbf{c}^T R \mathbf{c}. \end{aligned} ∫[Dmx(t)]2 dt=∫Dm[Φ(t)Tc]T[Φ(t)Tc] dt=∫cTDmΦ(t)DmΦ(t)Tc dt=cTRc.
R R R is known as the penalty matrix.
The penalized least squares estimate for c \mathbf{c} c is now
c ^ = [ Φ T W Φ + λ R ] − 1 Φ T W y . \hat{\mathbf{c}} = \big[ \mathbf{\Phi}^T W \mathbf{\Phi} + \lambda R \big]^{-1} \mathbf{\Phi}^T W \mathbf{y}. c^=[ΦTWΦ+λR]−1ΦTWy.
So we have
y ^ = Φ c ^ = Φ [ Φ T W Φ + λ R ] − 1 Φ T W y , \hat{\mathbf{y}} = \mathbf{\Phi} \hat{\mathbf{c}} = \mathbf{\Phi} \big[ \mathbf{\Phi}^T W \mathbf{\Phi} + \lambda R \big]^{-1} \mathbf{\Phi}^T W \mathbf{y}, y^=Φc^=Φ[ΦTWΦ+λR]−1ΦTWy,
which is still a linear smoother.
2.4.2 More general smoothing penalties
D 2 x ( t ) D^2 x(t) D2x(t) is only one way to measure the roughness of x x x.
If we were interested in D 2 x ( t ) D^2 x(t) D2x(t), we might think of penalizing D 4 x ( t ) D^4 x(t) D4x(t) ⇒ \Rightarrow ⇒ cubic polynomials are not rough.
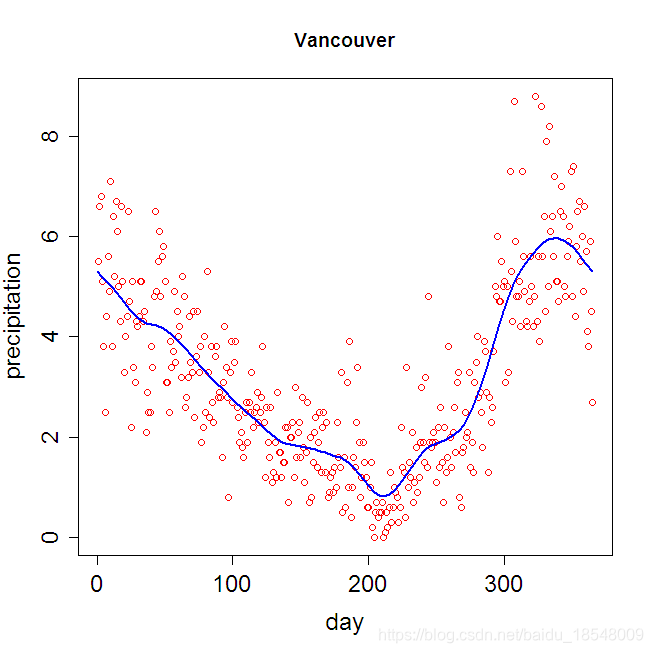
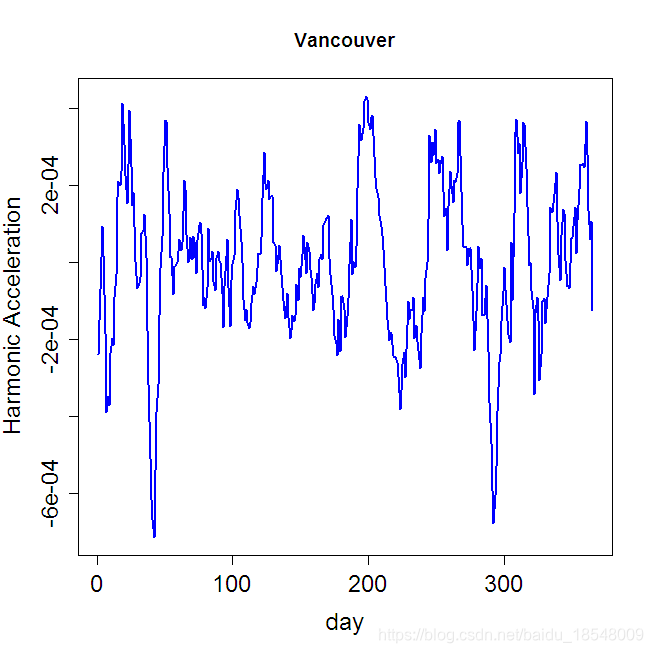
For Periodic data which is not very different from a sinusoid. The Harmonic acceleration of x ( t ) x(t) x(t) is
L x ( t ) = ω 2 D x ( t ) + D 3 x ( t ) . Lx(t) = \omega^2 D x(t) + D^3 x(t). Lx(t)=ω2Dx(t)+D3x(t).
Then L c o s ( ω t ) = L s i n ( ω t ) = 0 L cos(\omega t) = L sin(\omega t) = 0 Lcos(ωt)=Lsin(ωt)=0.
We can measure departures form a sinusoid by
J L ( x ) = ∫ [ L x ( t ) ] 2 d t . J_L(x) = \int \big[ Lx(t) \big]^2 ~ dt. JL(x)=∫[Lx(t)]2 dt.
|
| |
|
|
2.4.3 A very general notion
We can be even more general and allow roughness penalties to use any linear differential operator:
L x ( t ) = ∑ k = 1 m α m ( t ) D m x ( t ) . Lx(t) = \sum_{k = 1}^m \alpha_m (t) D^m x(t). Lx(t)=k=1∑mαm(t)Dmx(t).
Then x x x is “smooth” if L x ( t ) = 0 Lx(t) = 0 Lx(t)=0.
We will see later on that we can even ask the data to tell us what should be smooth.
However, we will rarely need to use anything so sophisticated.
2.4.4 Linear smooths and degrees of freedom
- In least squares fitting, the degrees of freedom used to smooth the data is exactly k k k, the number of basis functions.
- In penalized smoothing, we can have k > n k > n k>n.
- The smoothing penalty reduces the flexibility of the smooth (i.e. we know something).
- The degrees of freedom are controlled by
λ
\lambda
λ. A natural measure turns to be
d f ( λ ) = t r a c e S λ , S λ = Φ [ Φ T Φ + λ R ] − 1 Φ T . \begin{aligned} & df(\lambda) = traceS_\lambda, \\\\ & S_\lambda = \mathbf{\Phi} \big[ \mathbf{\Phi}^T \mathbf{\Phi} + \lambda R \big]^{-1} \mathbf{\Phi}^T. \end{aligned} df(λ)=traceSλ,Sλ=Φ[ΦTΦ+λR]−1ΦT.
Vancouver precipitation above was fit with 365 basis functions, and λ = 1 0 4 \lambda = 10^4 λ=104 resulting in d f = 12.92 df = 12.92 df=12.92.
2.4.5 Choosing the smoothing parameters: Cross Validation
There are a number of data-driven methods for choosing smoothing parameters.
- Ordinary Cross Validation: leave one point out and see how well you can predict it. For any linear smooth
O C V ( λ ) = ∑ ( y i − x ^ − i ( t i ) ) 2 = 1 n ∑ ( y i − x λ ( t i ) ) 2 1 − S λ ( i i ) , \begin{aligned} OCV(\lambda) & = \sum \big(y_i - \hat{x}_{-i}(t_i) \big)^2 \\\\ & = \frac{1}{n} \sum \frac{\big( y_i - x_{\lambda} (t_i) \big)^2}{1 - S_{\lambda (ii)} } , \end{aligned} OCV(λ)=∑(yi−x^−i(ti))2=n1∑1−Sλ(ii)(yi−xλ(ti))2,
where S S S is the smoothing matrix. - Generalized cross validation:
G C V ( λ ) = n − 1 ∑ ( y i − x ( t i ) ) 2 [ n − 1 t r a c e ( I − S ) ] 2 = ( n n − d f ( λ ) ) ( S S E n − d f ( λ ) ) . \begin{aligned} GCV(\lambda) &= \frac{n^{-1} \sum \big( y_i - x(t_i) \big)^2}{[n^{-1} trace(I - S)]^2} \\ & \\ &= \Big( \frac{n}{n - df(\lambda)} \Big) \Big( \frac{SSE}{n - df(\lambda)} \Big). \\ \end{aligned} GCV(λ)=[n−1trace(I−S)]2n−1∑(yi−x(ti))2=(n−df(λ)n)(n−df(λ)SSE).- S S E SSE SSE is discounted for degrees of freedom like usual, but we them also make a discount for minimizing over λ \lambda λ.
- G C V GCV GCV smooths more than O C V OCV OCV; even then, it may need to be tweaked a little to produce pleasing results.
- Various information criteria: A I C AIC AIC, B I C BIC BIC…
- ReML estimation
2.5 Summary
Smoothing penalities used to penalize roughness of the result.
- L x ( t ) = 0 Lx(t) = 0 Lx(t)=0 defines what is smooth.
- Commonly L x ( t ) = D 2 x ( t ) ⇒ Lx(t) = D^2x(t) \Rightarrow Lx(t)=D2x(t)⇒ straight lines are smooth.
- Alternative: L x ( t ) = D 3 x ( t ) + w 2 D x ( t ) ⇒ Lx(t) = D^3 x(t) + w^2 Dx(t) \Rightarrow Lx(t)=D3x(t)+w2Dx(t)⇒ sinusoids are smooth.
- Departures from smoothness traded off against fit to data.
- G C V GCV GCV used to dicide on trade off; other possibilities availabe.
3 Descriptive statistics for functional data
Summary statistics:
- Mean: x ˉ ( t ) = 1 n ∑ x i ( t ) ; \bar{x} (t) = \frac{1}{n} \sum x_i(t); xˉ(t)=n1∑xi(t);
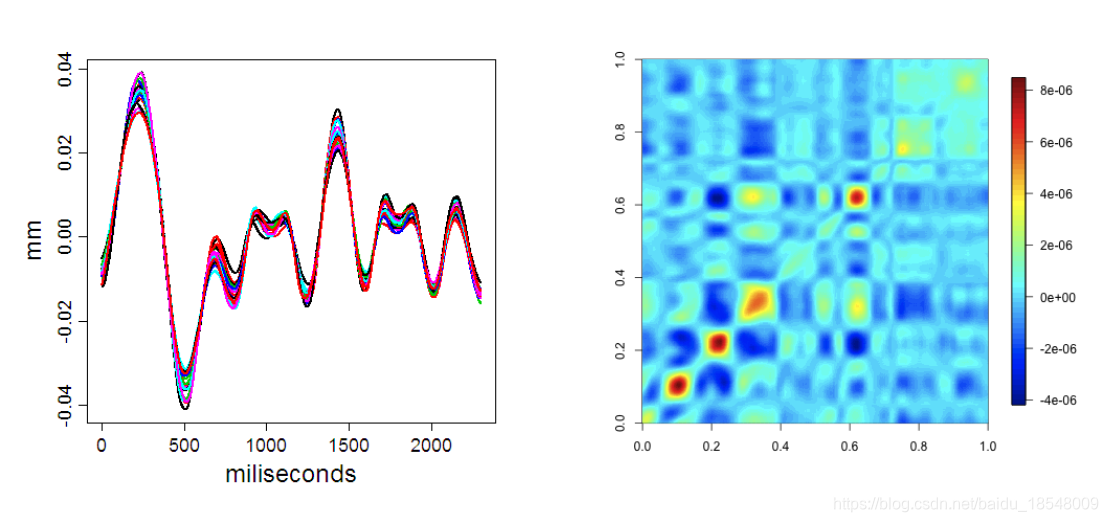
- Covariance:
σ ( s , t ) = c o v ( x ( s ) , x ( t ) ) = 1 n ∑ ( x i ( s ) − x ˉ ( s ) ) ( x i ( t ) − x ˉ ( t ) ) ; \begin{aligned} \sigma (s, t) &= cov(x(s), x(t)) \\\\ &= \frac{1}{n} \sum \big( x_i (s) - \bar{x}(s) \big) \big( x_i (t) - \bar{x}(t) \big); \end{aligned} σ(s,t)=cov(x(s),x(t))=n1∑(xi(s)−xˉ(s))(xi(t)−xˉ(t));
Covariance surfaces provide insight but do not describe the major directions of variation; - Correlation:
ρ ( s , t ) = σ ( s , t ) σ ( s , s ) σ ( t , t ) . \rho(s, t) = \frac{\sigma (s, t)}{\sqrt{\sigma (s, s)} \sqrt{\sigma (t, t)}}. ρ(s,t)=σ(s,s)σ(t,t)σ(s,t).
4 R example
4.1 New functions
| Functions used | Detials |
|---|---|
smooth.basis() | |
int2Lfd() | Convert integer to linear differential operator |
vec2Lfd(vectorCoef, rangeval = vectorRange) | Make a linear differential operator object from a vector |
fdPar() | Define a functional parameter object |
plotfit.fd | |
| `` | |
| `` | |
| `` | |
| `` | |
| `` | |
| `` |
Firstly, load up the library and the data.
par(ask = FALSE)
library("fda")
data(CanadianWeather)
temp <- CanadianWeather$dailyAv[ , , 1]
precip <- CanadianWeather$dailyAv[ , , 2]
daytime <- (1:365) - 0.5
day5 <- seq(0, 365, 5)
dayrng <- c(0, 365)
Fit the temperature data with b-spline basis without smoothing.
bbasis <- create.bspline.basis(dayrng, nbasis = 21, norder = 4)
tempSmooth1 <- smooth.basis(daytime, temp, bbasis)
plot(tempSmooth1)
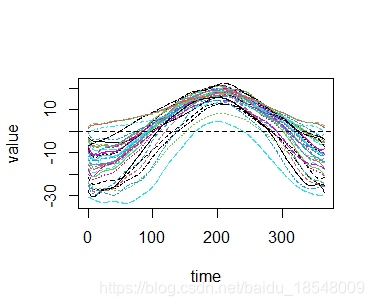
Using smooth functions.
4.1 Lfd objects
# Two common means of generating Lfd objects.
# 1/ int2Lfd -- just penalize some derivatives.
curv.Lfd <- int2Lfd(2) # penalize the squared acceleration
# 2/ vec2Lfd -- a (constant) linear combination of derivatives; for technical
# reasons this also requires the range of the basis.
harm.Lfd <- vec2Lfd(c(0, (2*pi/365)^2, 0), rangeval = dayrng)
Looking inside these objects is not terribly enlightening.
4.2 fdPar objects
We’ll concentrate on B-splines and second-derivative penalties.
# First, a value of lambda (purposefully large so that we can distinguish a
# fit from data below).
lambda <- 1e6
# Now define the fdPar object.
curv.fdPar <- fdPar(bbasis, curv.Lfd, lambda)
4.3 Smoothing functions
# We're now in a position to smooth.
tempSmooth1 <- smooth.basis(daytime, temp, curv.fdPar)
# Let's look at the result.
names(tempSmooth1)
# [1] "fd" "df" "gcv" "beta" "SSE" "penmat" "y2cMap"
# [8] "argvals" "y"
# Plot it.
plot(tempSmooth1$fd)
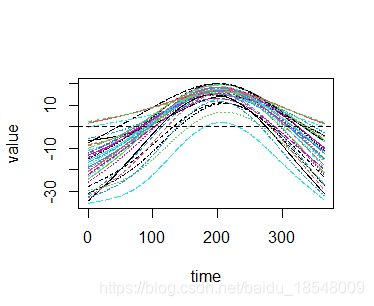
# There is also a neat utility to go through each curve in turn and look at
# its fit to the data.
par(mfrow = c(2,2))
plotfit.fd(temp, daytime, tempSmooth1$fd, index = 1:4)
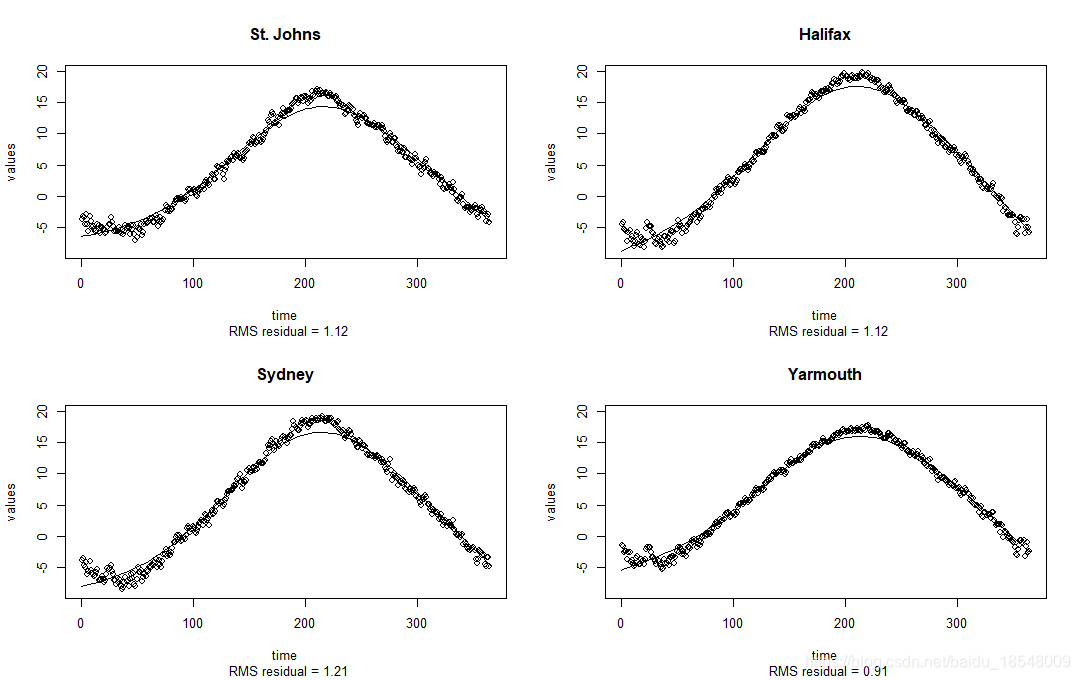
4.4 Examine some fit statistics
# degrees of freedom
tempSmooth1$df
# [1] 5.06577
# Just about equivalent to fitting 5 parameters.
# We'll also look at GCV, this is given for each observation.
tempSmooth1$gcv
# St. Johns Halifax Sydney Yarmouth Charlottvl Fredericton
# 1.2795697 1.2916752 1.5058050 0.8453872 1.5282543 1.5145976
# Scheffervll Arvida Bagottville Quebec Sherbrooke Montreal
# 2.1866513 2.0339306 1.8815098 1.5730488 1.8063912 1.6288147
# Ottawa Toronto London Thunder Bay Winnipeg The Pas
# 1.6414521 1.4650397 1.4648668 1.4939418 1.9590623 2.0175589
# Churchill Regina Pr. Albert Uranium City Edmonton Calgary
# 2.5650108 1.7818144 2.1515356 3.4367165 1.9083830 1.5607955
# Kamloops Vancouver Victoria Pr. George Pr. Rupert Whitehorse
# 0.9614403 0.4837343 0.4492183 0.9754061 0.4195135 1.9692874
# Dawson Yellowknife Iqaluit Inuvik Resolute
# 3.6711783 3.6956002 2.9828132 6.8113863 4.7486237
4.5 A more realistic value of lambda
lambda <- 1e1
curv.fdPar$lambda <- lambda
tempSmooth <- smooth.basis(daytime, temp, curv.fdPar)
#Repeat the previous steps
par(mfrow = c(2,2))
plotfit.fd(temp, daytime, tempSmooth$fd, index = 1:4)
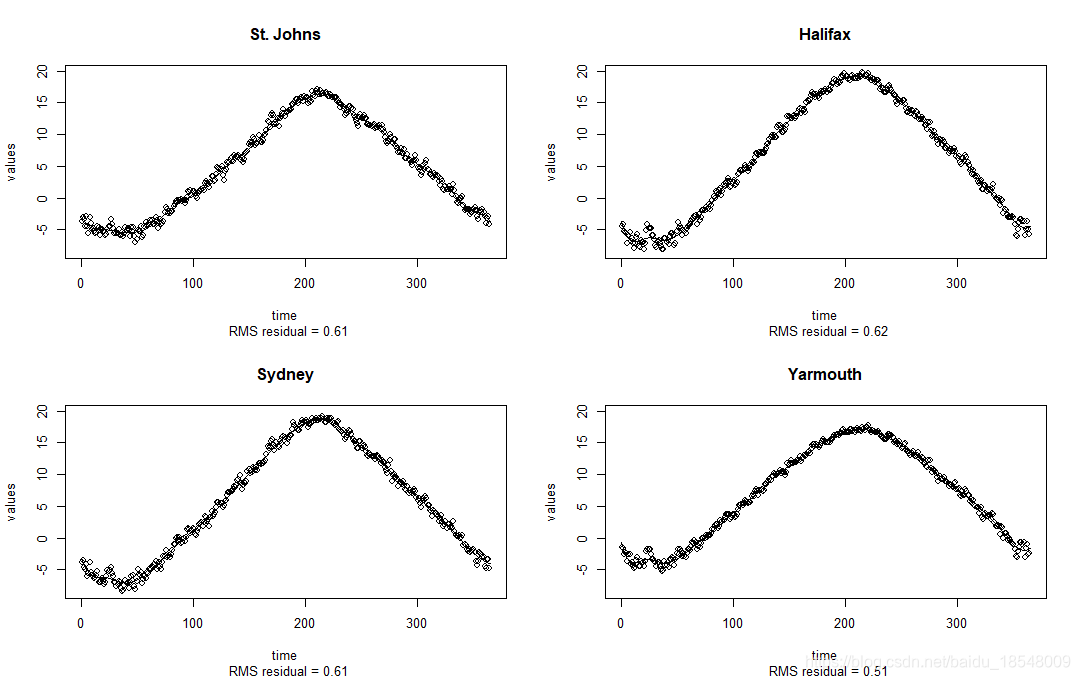
tempSmooth$df
# [1] 20.88924
tempSmooth$gcv
# St. Johns Halifax Sydney Yarmouth Charlottvl Fredericton
# 0.4186354 0.4301329 0.4209142 0.2948393 0.4788182 0.5038863
# Scheffervll Arvida Bagottville Quebec Sherbrooke Montreal
# 0.6742076 0.8735580 0.6212167 0.4722118 0.7790845 0.5541590
# Ottawa Toronto London Thunder Bay Winnipeg The Pas
# 0.5271093 0.4824045 0.4844556 0.4354220 0.5641720 0.5892378
# Churchill Regina Pr. Albert Uranium City Edmonton Calgary
# 0.6442146 0.5819684 0.6429497 1.0420690 0.6471629 0.7837149
# Kamloops Vancouver Victoria Pr. George Pr. Rupert Whitehorse
# 0.3360671 0.1172343 0.1318441 0.5298761 0.1653976 1.0228183
# Dawson Yellowknife Iqaluit Inuvik Resolute
# 1.0459365 0.7375391 0.5248940 1.0594254 0.3209614
Here the fit looks a lot better and the gcv values are much smaller.
4.6 Choosing smoothing parameters
We can search through a collection of smoothing parameters to try and find an optimal parameter.
We will record the average gcv and choose lambda to be the minimum of these.
lambdas <- 10^seq(-4, 4, by = 0.5) # lambdas to look over
mean.gcv <- rep(0, length(lambdas)) # store mean gcv
for(ilam in 1:length(lambdas)){
# Set lambda
curv.fdPari <- curv.fdPar
curv.fdPari$lambda <- lambdas[ilam]
# Smooth
tempSmoothi <- smooth.basis(daytime, temp, curv.fdPari)
# Record average gcv
mean.gcv[ilam] <- mean(tempSmoothi$gcv)
}
# We can plot what we have
par(mfrow = c(1, 1))
plot(lambdas, mean.gcv, type = 'b', log = 'x')
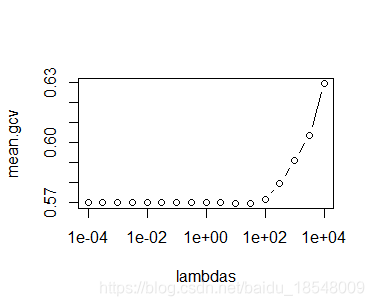
Select the lowest of these and smooth.
best <- which.min(mean.gcv)
lambdabest <- lambdas[best]
curv.fdPar$lambda <- lambdabest
tempSmooth <- smooth.basis(daytime, temp, curv.fdPar)
And look at the same statistics
par(mfrow = c(2,2))
plotfit.fd(temp, daytime, tempSmooth$fd, index = 1:4)
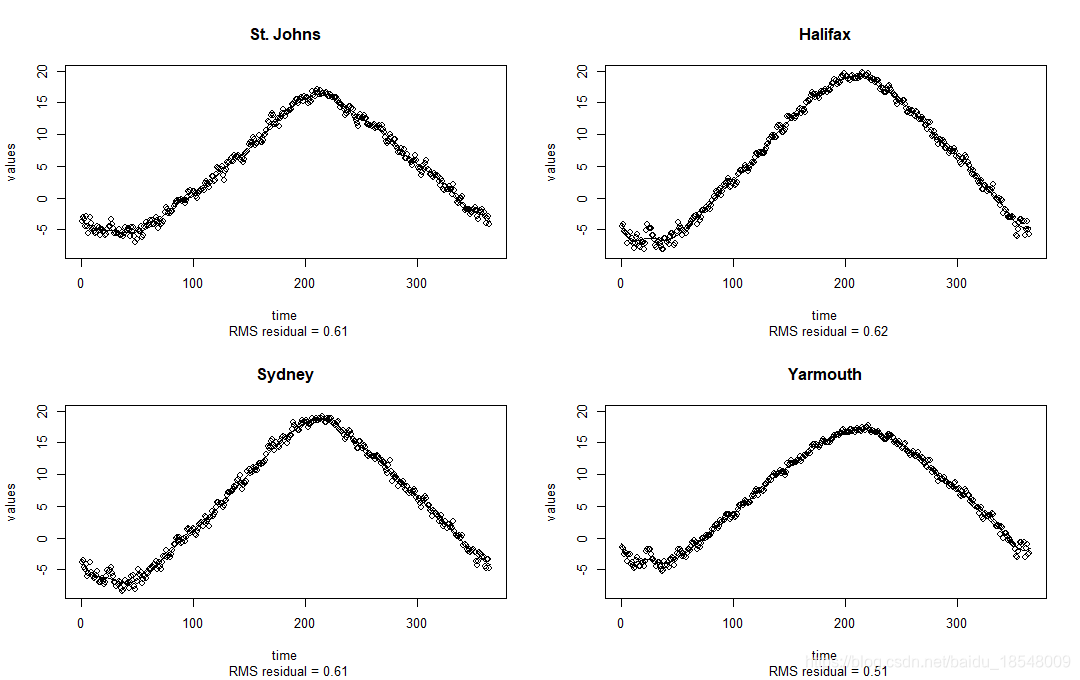
tempSmooth$df
# [1] 20.67444
# We'll also plot these
par(mfrow = c(1, 1))
plot(tempSmooth)
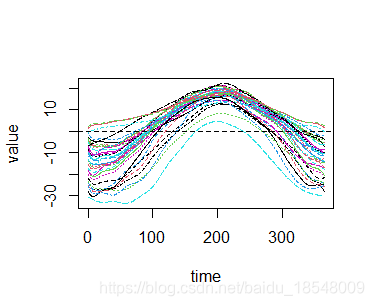
Functional data objects: manipulations and statistics
Now that we have a functional data object we can manipulate them in various ways. First let’s extract the fd object.





















 563
563











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








