Batch Renormalization-CSDN博客

本文链接：https://blog.csdn.net/baidu_32173921/article/details/65448478

Batch normalization

统计学上有一个问题叫Internal Covariate Shift，我也不知道该怎么翻译，暂且叫它ICS吧。说的是这样一个事情，即在偏统计的机器学习中，有这样一个假设，要求最初的数据的分布和最终分类结果的数据分布应该一致，一般来讲它们的条件分布应该是相同的 $P_{data}(Y|X=x)=P_{target}(Y|X=x)$ ，但是它们的边缘密度就不一定了， $P_{data}(X)\ne P_{target}(X)$ ，在我们的神经网络中，相当于每一层都是对原数据的一个抽象映射和特征提取，但是对于每一层来说，我们的target是一致的，可我们每一层都是一个映射啊，数据的边缘分布肯定是不一样的，这时候就尴尬了。

可我们的BN做的是这样一个事情，把它变成一个0均值1方差的分布上（不包括后面修正），这样在一定程度上，可以减小ICS带来的影响，可是也不是完全解决，毕竟你只保证了均值和方差相同，分布却不一定相同。

BatchRenormalization

本文系batch norm原作者对其的优化，该方法保证了train和inference阶段的等效性，解决了非独立同分布和小minibatch的问题。其实现如下：

其中r和d首先通过minibatch计算出，但stop_gradient使得反传中r和d不被更新，因此r和d不被当做训练参数对待。试想如果r和d作为参数来更新，如下式所示：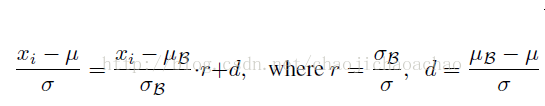

这样一来，就相当于在训练阶段也使用moving averages  μ和σ，这会引起梯度优化和normalization之间的冲突，优化的目的是通过对权重的scale和shift去适应一个minibatch，normalization则会抵消这种影响，而moving averages则消除了归一化后的激活对当前minibatch的依赖性，使得minibatch丧失了对每次权重更新方向的调整，从而使得权重尺度因normalization的抵消而无边界的增加却不会降低loss。而在前传中r和d的仿射变换修正了minibatch和普适样本的差异，使得该层的激活在inference阶段能得到更有泛化性的修正。

这样的修正使得minibatch很小甚至为1时的仍能发挥其作用，且即使在minibatch中的数据是非独立同分布的，也会因为这个修正而消除对训练集合的过拟合。

从Bayesian的角度看，这种修正比需要自己学习的scale和shift能更好地逆转对表征的破坏，且这种逆转的程度是由minibatch数据驱动的，在inference时也能因地制宜，而scale和shift对不同数据在inference时会施加相同的影响，因此这样的修正进一步降低了不同训练样本对训练过程的影响，也使得train和inference更为一致。