如何用另一种方式描述矩阵——特征值与特征向量

——是否可以将矩阵变换看作对某个状态的一步操作

接上文，我们提到了矩阵的逆，探讨了矩阵变换可看作是旋转和伸缩的组合，根据这个思路去寻找求矩阵逆的方式，最后也提到了一个问题：矩阵可以先伸缩再旋转，也可以先旋转再伸缩达到最终形态，是不是意味着矩阵有个共性的变换特征呢？这里我们参考矩阵乘法可交换条件文中提到的一个例子，假设矩阵的伸缩与旋转变换可以简单看作坐标值的倍乘与加数。如向量L:（1，0）经矩阵变换为坐标为：（2，1），可以将其看作是横坐标乘以2，再纵坐标加1，也可以看作是纵坐标加1，再横坐标乘以2。那么我能否将其看成是纵坐标加0.5后再与横坐标一起乘以2呢？用代数来表达就是 2a , b+1 = 2(a ,(b+1)/2）。 而是否存在向量（a，b）使得：2（a，(b+1)/2） = n（a，b）呢？即拉伸2倍后与原来是共线的呢？对于上面这个例子，（1，1）是满足的。但是要注意到，若是在Y轴上仅有伸缩变换，纵坐标为0的向量是无法体现的，当然这也是正交坐标系的某一个优势。

到此，我们不如先放下空间上的脑补，在矩阵乘法里我们已经探讨了矩阵乘法的物理意义的同时，也分析了代数表达式的几何反映，现在让我们再看一下矩阵乘法的代数表达式:C = AB，则：

A：,B： ,则C： 。

我们可以看出，对于向量 (x1,y1) 变换后的结果为：（x1x1' + y1x2',  x1y1'+y1y2'）。我们已经说过了其结果即为：以矩阵B的两个行向量的横、纵坐标权值和。于此同时我们可以类似上面思考的方式，将其试着用一个乘法运算表达：

（x1x1' + y1x2', x1y1'+y1y2'）=  ( x1* (x1' + y1x2'/x1) ,  y1* (x1y1'/y1 + y2') )。所以只需要求得向量（x1,y1）满足： (x1' + y1x2'/x1) = (x1y1'/y1 + y2')，即可求得与（x1,y1）共线的向量，且伸缩的大小就是：(x1' + y1x2'/x1) = (x1y1'/y1 + y2') 的长度。既然到了这一步，不妨就解出这个表达式的解吧：

移项：y1x2'/x1 = (x1y1'/y1 + y2') - x1'

通分：y1^2 = x1^2 * y1'/x2' + x1 * y1 * (y2'-x1')/x2'.

为了避免晃眼，将其他值改为系数： y^2 =  a x^2 + b xy.  ( a = y1'/x2', b = (y2'-x1')/x2')

二元二次方程：y^2 - bx y - a x^2 = 0. 

很明显。x =0始终有解（维度相同时，零向量当然是可以的），将x当作常数，直接用判别式计算，可求出两个解分别为：
y = bx + (b^2 + 4a)^1/2 x

y = bx - (b^2 + 4a)^1/2  x.

这时我们可以看出，是有两个解的（判别式大于0：b^2 + 4a > 0），且b和a决定了斜率。

当 4a = - b^2 时，只有一个解，当 4a < -b^2时，无解。

——特征向量的的结构

我们利用工具尝试画出几个定量的方程图像：

b = 0, a != 0时，a决定了图像与X轴（Y轴）的夹角，动作上可以认为是以X轴为镜像对称的两条线为轴：

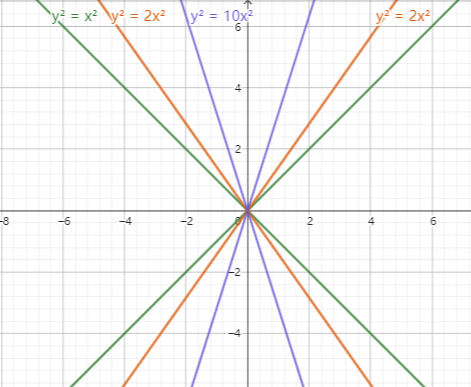
 b != 0, a != 0时，可以认为是a决定了图像与X轴（Y轴）的夹角，b（与a）决定了旋转的角度，动作上可以认为是以X轴为镜像对称的两条线，绕原点旋转一定角度为轴：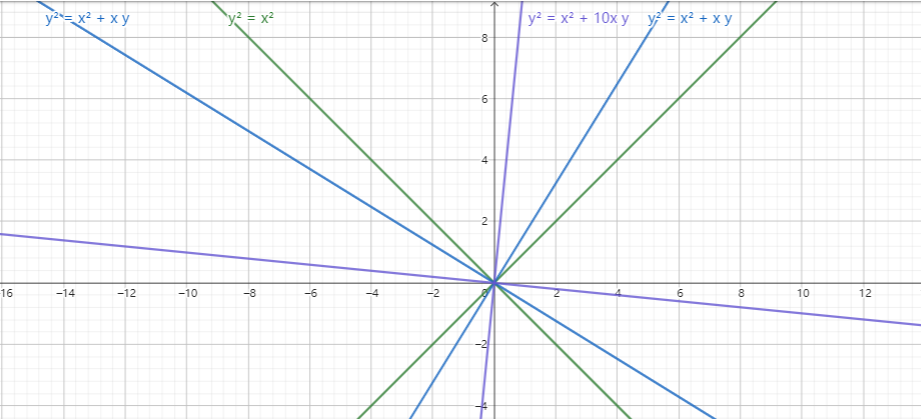

a = 0， b != 0时，X轴本身就是其中的一条线，b决定了另一条线与斜率为1的直线的角度，动作上可以认为是以X轴为一个轴，以斜率1为初始点，绕原点旋转一定角度为另一个轴：

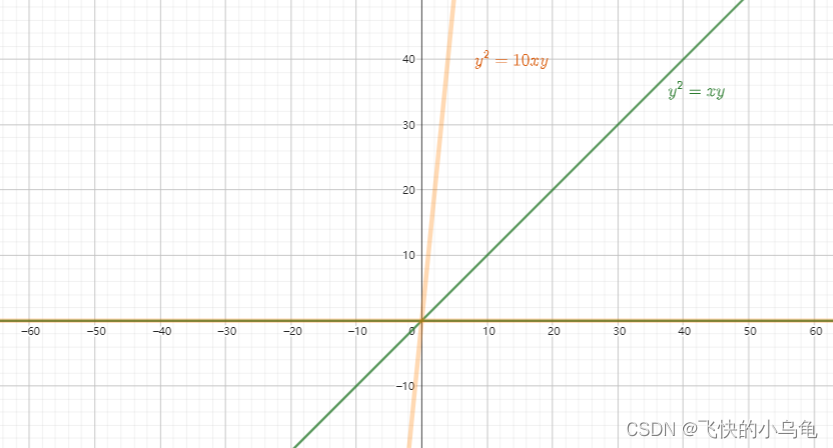
 当 a < 0时，b逐渐变大时，直到4a = - b^2 时（只有一个解），两条线的夹角逐渐变小，并最终成为一条线。而当继续调大b值（或者减小a值），将无解（或者说只有0解）。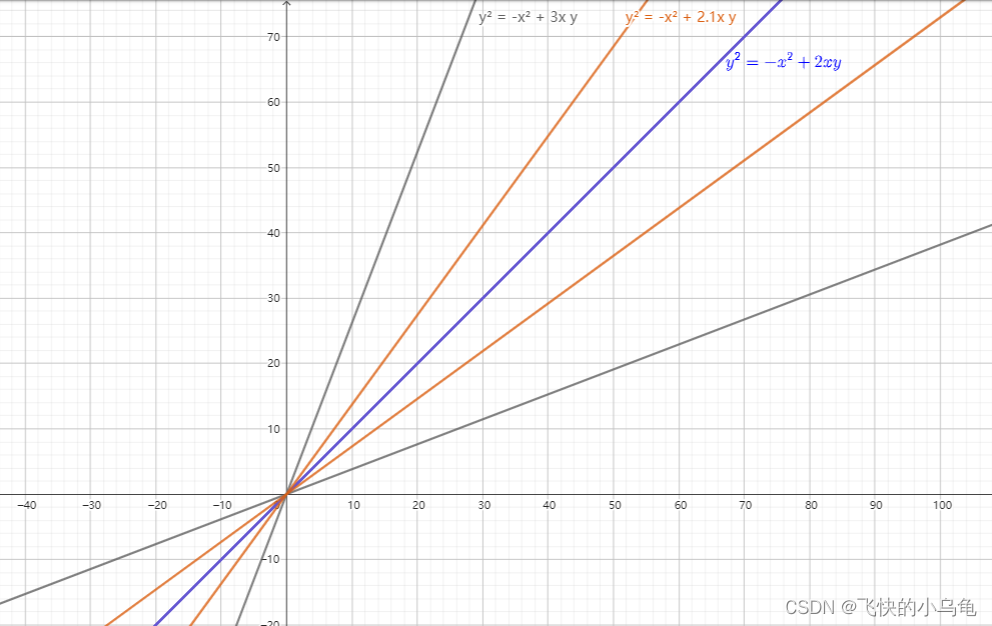

从上面的一些数据和图像中，其实我们已经可以看出端倪，一般情况下N维的矩阵应该最多就会有N个轴，但特殊情况会只有一个轴，以及没有轴。回头再去看看当初要求解的方程，可以看出其有二次型的影子（目前没有说到，权当一个联想，而且这也反映了有时候某些知识是相通的，或者某些知识的现实历史性，导致知识的场景与应用领域并非初衷，就好比矩阵刚开始是作为信息计算，解方程出现的，鸡你太美是作为歌曲出现的-囧）。

如果需要再详细点，再清楚点，那么几何上的操作与代数上的数据表达又是如何对应的呢？

下面我们再梳理一番慢慢探讨：

// TODO 下图作为行向量与列向量的思考