java数据结构与算法第一课——绪论

知行&

已于 2022-04-29 09:22:50 修改

阅读量769

点赞数

分类专栏：数据结构与算法（Java语言）文章标签：数据结构算法 java

于 2022-04-24 16:27:38 首次发布

本文链接：https://blog.csdn.net/baijaiyu/article/details/124329527

版权

数据结构与算法（Java语言）专栏收录该内容

11 篇文章 1 订阅

订阅专栏

一：什么是数据结构？

根据“百度百科”的定义，数据结构是相互之间存在一种或多种特定关系的数据元素的集合，即带“结构”的数据元素的集合。“结构”就是指数据元素之间存在的关系，分为逻辑结构和存储结构。

简单说来，计算机基本上就做两件事：存储数据和处理数据。数据结构，是老外总结出来的一套行之有效的数据存储方式，并围绕着这些存储方式设计出了一些高效的操作算法。借助数据结构，我们可以高效地管理多个数据，进而完成更复杂的功能。

需要注意的是，数据结构是一门单独的学科，与所使用的语言无关。数据结构是一种描述和组织数据的方式，我们可以使用任何语言实现数据结构。而在这一系列文章中，自然会使用到java语言进行具体的实现。

二：集合框架

数据结构具体包括哪些内容？基本如下图所示：

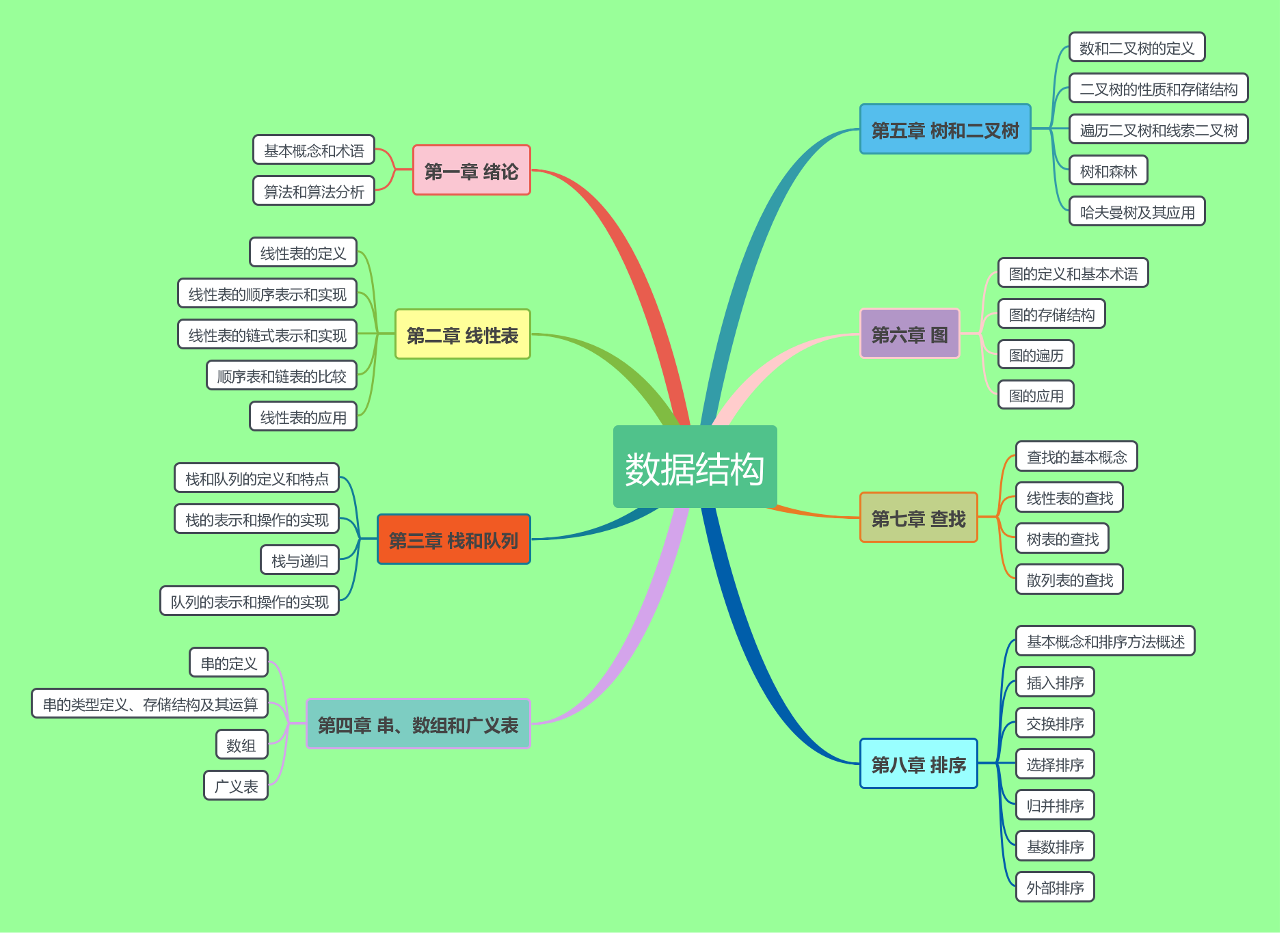
你可能会说，既然讲数据结构，何不直接开始讲解线性表、栈、队列、数组等内容，而要谈到什么集合框架呢？

集合框架，其实就是一大堆的集合类，这些类其实是java官方帮我们封装好的一些数据结构，即我们用到某个数据结构时，直接用java提供的对应的集合类即可。

集合框架是用于表示和操作集合的统一体系结构。所有集合框架都包含以下内容：

接口：这些是表示集合的抽象数据类型。接口允许独立于集合的表示细节来操作集合。在面向对象的语言中，接口通常形成层次结构。
实现：这些是集合接口的具体实现。从本质上讲，它们是可重用的数据结构。
算法：这些是对实现集合接口的对象执行有用计算（如搜索和排序）的方法。这些算法被称为多态的：也就是说，相同的方法可以用于适当集合接口的许多不同实现。从本质上讲，算法是可重用的功能。

下面我们来看一张图，先从宏观上理解集合框架。看这张图，我们重点要关注两项内容，即：

类和接口的关系；
接口和接口的关系。

我仅截取其中的一部分，简略地介绍一下此图：

我们学习的重点，就是以下四个接口；

学习的思路是，先了解一个数据结构的底层原理，再去了解这个数据结构再java中对应的集合类。

三：时间复杂度和空间复杂度

在学习正式的数据结构之前，需要一些准备知识，今天我会重点讲述时间复杂度和空间复杂度。

如何衡量一个算法的好坏呢？我们一般观其两项：时间效率和空间效率。时间效率被称为时间复杂度，空间效率则被称为空间复杂度。

时间复杂度主要衡量的是一个算法的运行速度，而空间复杂度主要衡量一个算法所需要的额外空间。在计算机发展的早期，计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展，计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度了。

3.1时间复杂度

算法中的基本操作的执行次数，为算法的时间复杂度。具体实例如下：

package Test;
public class TestDemo1 {
        static int func(int N){
            int count = 0;
            for (int i = 0; i < N; i++) {
                for (int j = 0; j < N; j++) {
                    count++;
                }
            }
                for (int k = 0; k < 2 * N; k++) {
                    count++;
                }
                int M = 10;
                while ((M--) > 0) {
                    count++;
                }
            
            return count;
        }

    public static void main(String[] args) {
        System.out.println(func(10));
    }
}

我不准备在这里显示运行结果，因为这并不重要，让我们把关注的重点放在这段代码的运行次数上。显然，func()函数的运行次数为：

如你所见，N越大，低次项对于最终运行次数的影响就越小，几乎可以忽略不计。实际中我们计算时间复杂度时，其实并不一定要计算精确的执行次数，而只需要大概执行次数，那么这里我们使用大O的渐进表示法。

【推导大O阶方法】

1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中，只保留最高阶项。
3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

需要注意的是，在实际中，我们一般关注的是算法的最坏运行情况，即任意输入规模的最大运行次数(上界) 。

接下来，我会列举一些常见算法的时间复杂度供大家参考学习：

3.1.1实例1

static void func2(int N) {
int count = 0;
for (int k = 0; k < 2 * N ; k++) {
count++;
}
int M = 10;
while ((M--) > 0) {
count++;
}
System.out.println(count);
}

准确来说是F(N)=2*N+10，根据我们的简化原则，其时间复杂度为O(N)。

3.1.2实例2

计算bubbleSort的时间复杂度？

经过这一趟冒泡排序，数组中最大的元素出现在了它应该出现的位置；下此进行比较时，无需再关注最后一个位置，因为它已经放置了数组中最大的元素；经过N-1趟冒泡排序，每趟都将1个数放在其应该出现的位置；最后一趟排序时将倒数第二小的数放在了下标为1的位置，同时下标为0处已经是该数组中最小的元素了，相当于最后一趟冒泡安放了2个数。所以，我们可以得出如下结论：

显然，对含有N个元素的整型数组进行排序，需要进行N-1趟冒泡排序，该算法的时间复杂度为O(N^2)。

3.1.3实例3

计算binarySearch的时间复杂度？

我们可以采用归纳法，得出该结论，具体推导如下图：

总结规律，得出结论：

binarySearch的时间复杂度为O(logn)。

3.1.4 实例4

计算斐波那契递归fibonacci的时间复杂度？

直接看不容易理解，我们任然遵循“从特殊到一般”的思想，通过总结规律，得出结论：

3.2空间复杂度

空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度。空间复杂度不是程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度计算规则基本与时间复杂度类似，也使用大O渐进表示法。

3.2.1实例1

// 计算bubbleSort的空间复杂度？
void bubbleSort(int[] array) {
        for (int end = array.length; end > 0; end--) {
                boolean sorted = true;
                for (int i = 1; i < end; i++) {
                        if (array[i - 1] > array[i]) {
                                Swap(array, i - 1, i);
                                sorted = false;
                        }
                }
                if (sorted == true) {
                break;
                }

        }

}

实例1使用了常数个额外空间，所以空间复杂度为 O(1)。需要注意的是，数组内存的开辟是必须进行的步骤，否则数组就没有安身之地了，这不属于额外消耗的空间；你也可以认为这是临时占用的空间。

3.2.2实例2

// 计算fibonacci的空间复杂度？
int[] fibonacci(int n) {
long[] fibArray = new long[n + 1];
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; i++) {
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray;
}

实例2动态开辟了N个空间，空间复杂度为 O(N)。

3.2.3实例3

// 计算阶乘递归Factorial的空间复杂度？
long factorial(int N) {
return N < 2 ? N : factorial(N-1)*N;
}

实例3递归调用了N次，开辟了N个栈帧，每个栈帧使用了常数个空间。空间复杂度为O(N)。

我们已经强调过，计算机行业之发展日新月异，计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度了。

本课内容结束！

知行&

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
java数据结构与算法第一课——绪论

一：什么是数据结构？根据“百度百科”的定义，我们可以说，数据结构是相互之间存在一种或多种特定关系的数据元素的集合，即带“结构”的数据元素的集合。“结构”就是指数据元素之间存在的关系，分为逻辑结构和存储结构。简单说来，计算机基本上就做两件事：存储数据和处理数据。数据结构，是老外总结出来的一套行之有效的数据存储方式，并围绕着这些存储方式设计出了一些高效的操作算法。借助数据结构，我们可以高效地管理多个数据，进而完成更复杂的功能。二：数据结构的重要性？...
复制链接

扫一扫