我的LaTeX秘籍（不断更新中）

此贴乃是我个人的一些经验总结。当然书上都能轻易找到的东西不用我在这赘述，这里我所罗列的很多可能都是平常不太会用到的奇技淫巧，但若是遇到其中一二，怕也难免抓耳挠腮。日积月累，越来越多，遂记于此处备忘备查。如果能帮到谁，荣幸之至，但余更希望诸君永远不会遇到这些麻烦。

欢迎关注白马负金羁的博客 http://blog.csdn.net/baimafujinji，为保证公式、图表得以正确显示，强烈建议你从该地址上查看原版博文。本博客主要关注方向包括：数字图像处理、算法设计与分析、数据结构、机器学习、数据挖掘、统计分析方法、自然语言处理。

---

关于算法的排版

文章里面以伪代码的形式来给出算法的流程介绍应该说是比较常见的做法。但在既定的LaTeX模板里面调整缩进其实是一件特别麻烦的事情！例如，排下面一段伪代码（图1），我需要写这么一大堆东西：

\par Input: Data set $D$
\\
\hangafter 1 \hangindent 5.1em \noindent
Distance function $f$ (e.g., Euclidean distance)
\par //Initialisation: the whole data space needs to be insepected
\\
\hangafter 1 \hangindent 3.5em \noindent
$\mathcal{T}={(\infty,\infty)}$
\par //Loop: iterate until all regions have been investigated
\\
\hangafter 1 \hangindent 3.5em \noindent
WHILE ($\mathcal{T}\not=\emptyset$) DO\\
\hangindent 3.5em \indent
$(m_x,m_y)$=takeElement($\mathcal{T}$)\\
\hangindent 3.5em \indent
IF($\exists$ boundedNNSearch($O, D, (m_x,m_y), f$)) THEN\\
\setlength{\parindent}{1.8cm}
\hangindent 3.5em \indent
$(n_x, n_y) = $boundedNNSearch($O, D, (m_x,m_y), f$))\\
\hangindent 3.5em \indent
$\mathcal{T}=\mathcal{T}\cup{(n_x, n_y),(m_x, m_y)}$\\
\hangindent 3.5em \indent
OUTPUT $n$\\
\setlength{\parindent}{1cm}
\hangindent 3.5em \indent
END IF\\
\hangafter 1 \hangindent 3.5em \noindent
END WHILE\\

当然，上面这段代码也并非一无是处。我之所以把这个“反面教材”列在这里，因为其中的缩进技巧仍然非常有用。如果你要在文段中做一些“私人订制”式的缩进，那么上面的代码已经可以帮你解决绝大部分的问题了！

图1

下面我们来介绍正规的代码排版该如何做，答案就是用一些现成的包。我这里之所以说“一些”，那是因为根据不同的风格要求，实现代码排版的包其实有很多。我这里仅仅以algorithm2e包为例来做演示。其实你可以看到引用该包时，参数linesnumbered用来控制是否要给行编号，参数boxed控制是否要给算法加边框。

\usepackage[linesnumbered,boxed]{algorithm2e}

\begin{algorithm} \SetAlgoNoLine
\caption{The \textit{GeoGreedy} Algorithm} 
\KwIn{A data set of $d$-dimensional points $D$ and a desired output size $k$.} 
\KwOut{A subset of $D$ of size $k$, denoted by $S$.} 
$S\leftarrow \emptyset$\\
\For {each $i:=1, 2, \cdots , d$,} 
{
$p \leftarrow $ an $i$-th dimension boundary point of $D$\\
$S \leftarrow S\cup \{p\}$\
}
\For{each $i:=1, 2, \cdots , k-d$,}
{
find a point $p \in D \setminus S$ with the smallest critical ratio for $S$ (i.e., $cr(p,S)$)\\
\If{$cr(p,S)\geq 1$}
{
\textbf{return} $S$\\
}
\Else
{
$S \leftarrow S\cup \{p\}$\\
}
}
\textbf{return} $S$\
\end{algorithm}

上述代码的排版效果如图2所示。

图2

---

控制列表项的行距与段间隔

这其实是一个挺tricky的事情。因为其实没有什么特别棒的自动化的解决方法（当然，如果你知道什么更好的方法请别忘了告诉我）。如图3所示，列表项中每一个item的间距都比较大，而且item和前后的正文段落间也有很大的间距。正常情况下，这并不会影响观感。

图3

但是，如果你的每一个item只有短短几个词，那么各个item之间间隔过大就很丑陋了。这是你需要像下面这样来“半自动”地调整间隔，说是半自动，那是因为这个间隔是由你人为设定的。你可以自己试试，如果不采用下面的方法，而使用一般的排法，会得到什么样的结果。下面示例代码中的\vspace{-0.8em}用来控制首尾items和正文段落之间的距离。

In this paper, there types of utility functions are considered: 
\begin{itemize}[leftmargin=3.2em]
\vspace{-0.8em}
\setlength{\itemsep}{0pt}
\setlength{\parsep}{0pt}
\setlength{\parskip}{0pt}
\item Convex Function
\item Concave Function
\item Constant Elasticity of Substitution (CES) Function. 
\vspace{-0.8em}
\end{itemize}

图4

---

自定义方法输入argmax型公式

在LaTeX中输入像max, min之类的公式并没什么问题，因为它们都是内置的。但是输入argmax公式可能要稍微复杂一些。下面给出示例代码：

\usepackage{amsmath}
\usepackage{amssymb}
\DeclareMathOperator*{\argmax}{argmax}

$$p_i^* = \mathop{\argmax}_{p\in{D}}{(p[i])}$$

效果如图5所示。

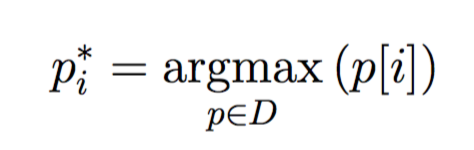
图5

---

多行公式的对齐

当你写多行公式时，特别是一些计算过程时，你往往要指定公式的对齐点，当然方法仍然有很多，下面是其中一种解决方式。注意代码中的align*，这里* 的意思就是不对每行公式编号。所以如果你删掉这个星号，公式的每行都会被编号。

Also, we can conclude the the following inequalities
\begin{align*}
\sum\limits_{i=1}^{d-1}(p[i]-s[i])\cdot v[i] &\leq \sum\limits_{i=1}^{d-1}\frac{c_i}{t}v[i]\\
&\leq \frac{d-1}{t} \max_{i\leq d-1}{(c_iv[i])}\\
&\leq \frac{d-1}{t} \max_{i\leq d-1}{(p_i^* \cdot v)}
\end{align*}

上述的代码的执行结果如图6所示。

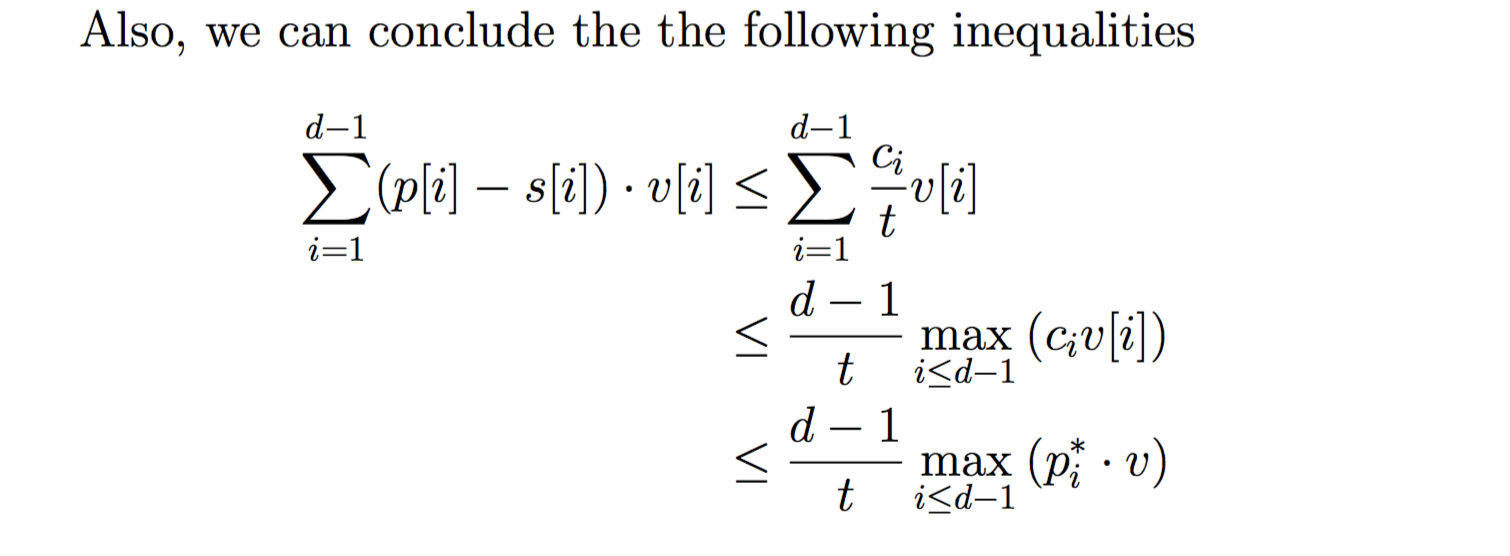
图6

---

关于参考文献

编写参考文献的方法有很多，一般资料上都找得到，我也不想在这些地方上浪费笔墨。当然，你可以hard-coding，如果文献不是特别多，文章也不是特别长，其中的引用地方也很simple，这也不是不可以。例如，

\begin{thebibliography}{1}
\bibitem{}
	Donald Kossmann, Frank Ramsak, Steffen Rost, 2002, 
	\emph{Shooting Stars in the Sky: An Online Algorithm for Skyline Queries}, 
	Proceedings of the 28th VLDB Conference, Hong Kong, China.
\end{thebibliography}

排出的效果如图7所示。

图7

但是，当References多了之后，特别是有多处引用的时候，这种Hard-coding的方法就会变得特别麻烦。所以这时我们就需要一个更方便的做法，其中最常被推荐使用的是 bibtex。其实它就是把参考文献的引用信息放到另外一个文件里进行管理，这个东东的使用方法网上一搜就有，这里不做过多解释。但是在用的时候还是可能会出现一些比较tricky的地方。第一个需要注意的是，在使用bibtex的时候，文中必须有显式的引用，如果你不引用它，文末的References列表里是不会出现相应的文献条目的。另外一个地方在于它的排序问题。我单独把这一点拉出来解释一下。先来看一段例子：

首先，文章正文的LaTeX源文件中，我们是像下面这样使用的：

\section{Overview}
Geometry approach for $k$-regret query is proposed in~\cite{peng2014geometry}. 
This new algorithm takes advantage of some geometry property to improve 
the performance of \textsc{Cube}~\cite{nanongkai2010regret}.

\bibliographystyle{unsrt}%
\bibliography{Ref_GeoApp}

其中，最后一行给出的Ref_GeoApp是我们自己命名的专门用来存放参考文献信息的文件（同时扩展名.bib）。它的内容示例如下：（通常这个文件中的信息并不需要自己写，从Google Scholar或者论文官网（例如 IEEE等）上可以直接找到下面这些信息，你只要简单的复制+粘贴即可。你也可以自己根据需要做调整。）

@inproceedings{peng2014geometry,
  title={Geometry approach for k-regret query},
  author={Peng, Peng and Wong, Raymond Chi-Wing},
  booktitle={ICDE},
  pages={772--783},
  year={2014}
}

@article{nanongkai2010regret,
  title={Regret-minimizing representative databases},
  author={Nanongkai, Danupon and Sarma, Atish Das and Lall, Ashwin and Lipton, Richard J and Xu, Jun},
  journal={Proceedings of the VLDB Endowment},
  volume={3},
  number={1-2},
  pages={1114--1124},
  year={2010}
}

然后我们排出来的正文效果如图8所示。

图8

相应的参考文献列表如图9所示。


图9

这里我特别要强调和补充的是“\bibliographystyle{unsrt}”中的unsrt，很多例子会使用plain，这是最基本的没有什么特殊要求的格式。但对于我们这个例子来说，它并不是一个好的选择。我们所使用的 unsrt 基本上跟 plain 类型一样，但参考文献的条目之编号是按照引用的顺序，而不是按照作者的字母顺序的。所以，如果你采用了plain，那么文章中比较奇怪的地方就是，段落里先出现的文献标号是[2]而不是[1]！这显然不合适。此外，还有一个 类似于 plain 类型的选择就是 alpha，此时参考文献的条目是基于作者名字和出版年份的顺序来编号的。

---

输入类似分段函数的大括号

类似图10这种分几种情况的大括号也偶尔会被用到，例如在描述一个分段函数的时候。

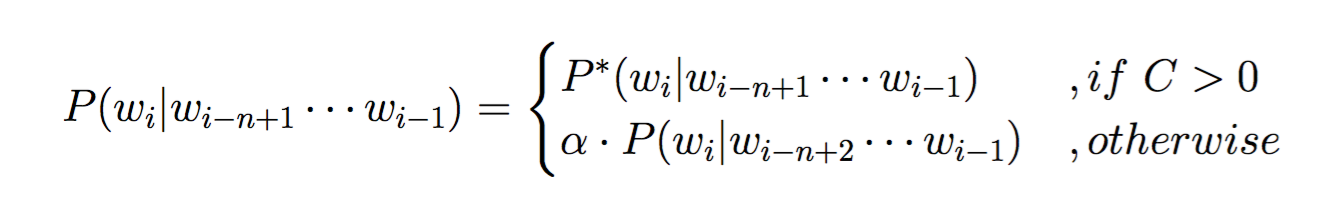
图10

下面的示例代码演示了上面公式的输入方法。

$$P(w_i|w_{i-n+1}\cdots w_{i-1})=\begin{cases}
P^*(w_i|w_{i-n+1}\cdots w_{i-1})&,if\  C>0\\
\alpha \cdot P(w_i|w_{i-n+2}\cdots w_{i-1})&,otherwise
\end{cases}$$

---

关于首行缩进的问题

一般情况下，即在你不做任何处理的时候，LaTeX默认，每一段都会有一个标准的缩进（类似中文每段开头空两格）。例如下面的代码会得到如图11所示的结果。

\documentclass[a4paper]{article}
\usepackage[utf8]{inputenc}

\title{A Study In Scarlet}
\author{Arthur Conan Doyle}
\date{}

\begin{document}
\maketitle

In the year 1878 I took my degree % 省略后续文字

注意，其中的\date{}表示省略日期信息。

图11

但如果我们给它加上一个Section标题，结果是每个Section的第一段都不会再缩进，之后的每段仍然会做缩进处理。例如下面的示例代码：

\documentclass[a4paper, 14pt]{extarticle}
\usepackage[utf8]{inputenc}

\title{\huge{\textsc{A Study In Scarlet}}}
\author{Arthur Conan Doyle}
\date{}

\begin{document}
\maketitle

\section*{Chapter 1 - Mr. Sherlock Holmes}
In the year 1878 I took my degree % 省略后续文字

请注意，我们同时调大了文章的字体，结果如图12所示。

图12

此时，为了让首段跟其他段落一样缩进，我们需要使用下面的代码：

\documentclass[a4paper, 14pt]{extarticle}
\usepackage[utf8]{inputenc}
\usepackage{indentfirst}
\setlength{\parindent}{2em}
\addtolength{\parskip}{3pt}

\title{\huge{\textsc{A Study In Scarlet}}}
\author{Arthur Conan Doyle}
\date{}

\begin{document}
\maketitle

\section*{Chapter 1 - Mr. Sherlock Holmes}
In the year 1878 I took my degree % 省略后续文字

注意，我们同时调整了段落的间距，结果如图13所示。

图13

---

如何输入矩阵

很多数学公式中需要用到矩阵，下面这段代码演示了矩阵的输入方法：

$$\mathbf{H}=
\begin{bmatrix} 
\frac{\partial^2f}{\partial x_1^2} & \frac{\partial^2f}{\partial x_1\partial x_2} & 
\cdots &\frac{\partial^2f}{\partial x_1\partial x_n} \\

 \frac{\partial^2f}{\partial x_2\partial x_1} & \frac{\partial^2f}{\partial x_2^2} &  
 \cdots &\frac{\partial^2f}{\partial x_2\partial x_n} \\

 \vdots & \vdots & \ddots & \vdots \\
\frac{\partial^2f}{\partial x_n\partial x_1}&\frac{\partial^2f}{\partial x_n\partial x_2}&
\cdots &\frac{\partial^2f}{\partial x_n^2} \end{bmatrix}$$

其结果如图14所示。

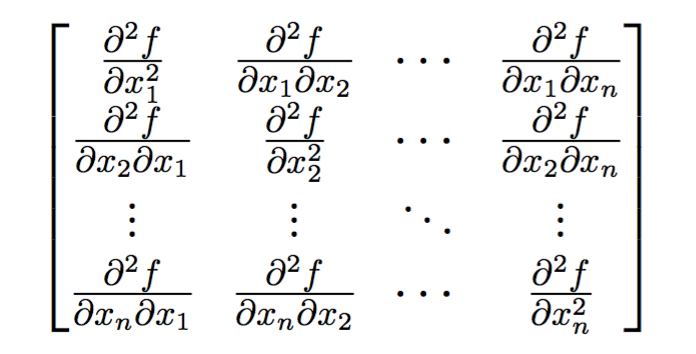
图14

---

行内公式显示模式的调整技巧

在行内输入公式时，可能会遇到一些麻烦。例如图15所示之情况（我们用红色方框标出）。比如我们希望max的下标能够出现在正下方，而非右下角。再比如，我们希望分数不会因为行距所限而被缩小显示。

图15

这时你所需要做的只是在相应的公式中加入\displaystyle，例如：

$\displaystyle \max_{p_u[i],p_v[i]\in[s_l,s_{l+1}]}|p_u[i]-p_v[i]|$
$\displaystyle \frac{c_i}{t}

如此一来，你所得到结果就会变成图16所示之结果。

图16

---

附录——常用数学符号表