生产函数是指在一定时期内,在技术水平不变的情况下,生产中所使用的各种生产要素的数量与所能生产的最大产量之间的关系。换句话说,生产函数反映了一定技术条件下投入与产出之间的关系。生产函数的一般形式为
Y = AF(K, L)
生产函数提供了投入与产出间的数量联系,上式显示产出(Y)取决于投入(资本K、劳动L)和技术水平(A),A有时也被称为“生产率”。在忽略技术进步时,生产函数可采用以下形式
Y = F(K, L)
如果满足以下性质,则称该生产函数是新古典生产函数:
1、对所有K>0和L>0,呈现出对每一种投入正、但递减的边际产出,即:
2、假定规模报酬不变,即Y=AF(λK,λL)=λAF(K, L),常用的柯布-道格拉斯生产函数即为一个典型例子
3、随着资本(或劳动)趋于零,资本(或劳动)的边际产品趋于无穷大;随着资本(或劳动)趋于无穷大,资本(或劳动)的边际产品趋于零,即生产函数满足Inada条件:
4、竞争性经济,从而要素按其边际产品(MPL或MPK)得到报酬(以柯布-道格拉斯生产函数为例),有:
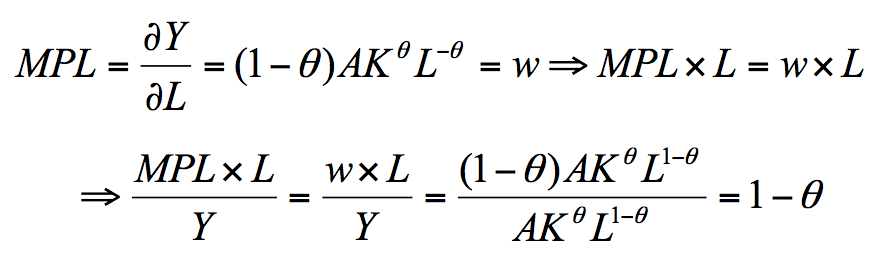
在上述两假定前提下,工资收入占国民收入的份额即为劳动对产出的贡献份额;同理,可证得:资本收入占国民收入的份额为θ,即资本对产出的贡献份额。
在此基础上,我们可推导出以下关系:
上式经济含义为:产出增长率=技术进步率+资本份额×资本增长率+劳动份额×劳动增长率
以及
上式的经济含义为:人均产出增长率=技术进步率+资本份额×人均资本增长率
(本文完)








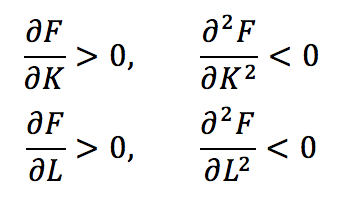
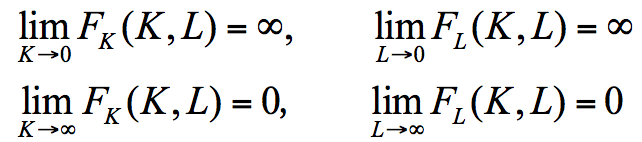
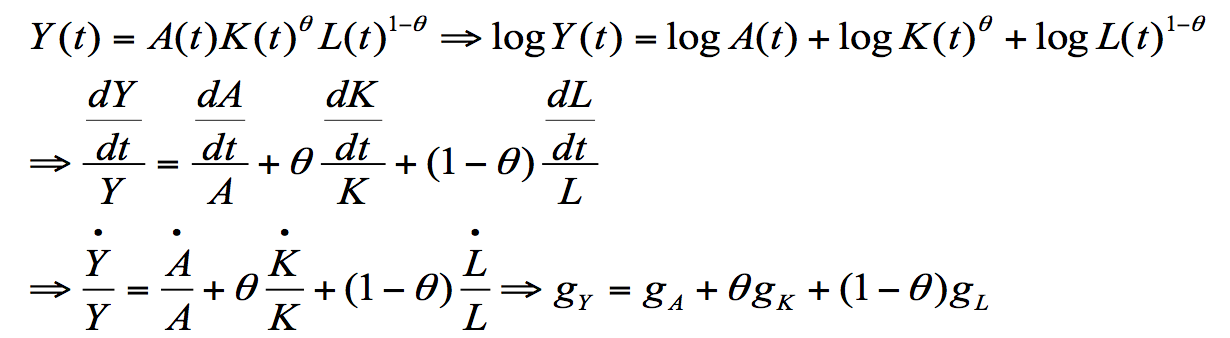
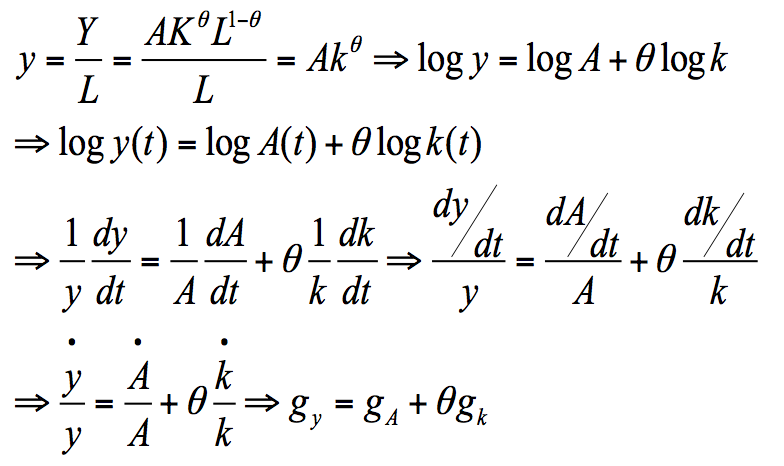

















 7341
7341

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










