在线性代数中,如果内积空间上的一组向量能够张成一个子空间,那么这一组向量就称为这个子空间的一个基。Gram-Schmidt正交化提供了一种方法,能够通过这一子空间上的一个基得出子空间的一个正交基,并可进一步求出对应的标准正交基。
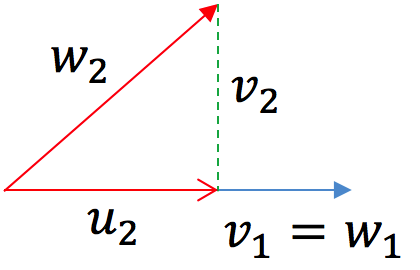
先来看下 k = 2 时的情况,此时,v1=w1。因为我们想得到一个与v1相垂直的向量v2,于是可以让w2向v1的方向上做投影。即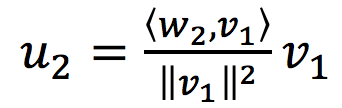
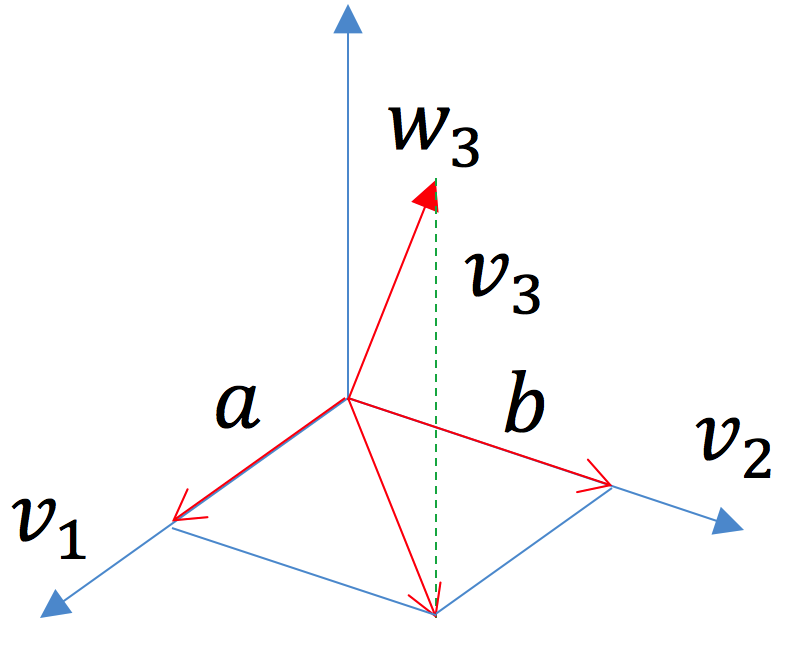
此时,。当 k = 3 时,v1和v2的找法就按照前面所示的过程来执行。如下图所示我们已经找到了两个垂直的基底v1和v2,下面来设法找到v3。如下图所示,a是w3在v1方向上的投影,b是是w3在v2方向上的投影,显然v3=w3-(a+b)=w3-a-b。
按照此过程继续下去,当k = n时,前n-1个彼此垂直的向量v1,...,vk-1已经构造完成,为了找到向量vk,我们将wk向v1,...,vk-1分别做投影,得到u1,...,uk-1,显然 vk = wk - u1 - ... - uk-1。这也就是所谓的“施密特正交化”。
施密特正交化过程告诉我们,对于一个有限维的空间,我们一定可以找到一组彼此垂直的基底。当我们得到这样一组基底后,还可以对它们进行归一化,便可得到orthonormal的基底。也就是说对于一个有限维的空间,一定存在一组orthonormal的基底。更加正式地,我们可以用下面的定理来表述。
(本文完)








 本文介绍在线性代数中如何使用Gram-Schmidt正交化方法从一个子空间的基构造出该子空间的正交基及标准正交基。通过逐步投影去除向量间的相关性,实现向量集的正交化。
本文介绍在线性代数中如何使用Gram-Schmidt正交化方法从一个子空间的基构造出该子空间的正交基及标准正交基。通过逐步投影去除向量间的相关性,实现向量集的正交化。



















 2368
2368

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










