离散数学学习笔记 第一章 集合

目录

集合的表示

1.枚举法

2.叙述法

3.文氏图

集合的基数

特殊集合 集合的关系

1.空集

2.全集

3.相等关系

元素的基本特性

外延性定理

 证明集合相等

4.包含关系

重要定理

5.幂集

集合的运算

集合的运算定律

*可数集合与不可数集合

1.等势

2.可数集合

 3.不可数集合

---

---

集合的表示

1.枚举法

A = {a, b, c, d}

B = {2, 4, 6, 8, 10,···}

2.叙述法

A = {x|x是英文字母中的元音字母}

B = {x|x ∈ Z, x < 10}

3.文氏图

一般使用平面上的方形或圆 形表示一个集合，而使用平面上的一个小圆点来表示集合的元素。

集合的基数

集合 A 中的元素个数称为集合的基数(base number)，记为 |A|

A = {a, b, c}, |A| = 3

B = { a, {b, c} } , |B| = 2 

特殊集合 集合的关系

1.空集

不含任何元素的集合叫做空集(empty set)，记作 ∅.

空集可以符号化为 ∅ = {x|x≠x}.

空集是绝对唯一的

2.全集

针对一个具体范围，我们考虑的所有对象的集合叫做全集(universal set)，记作 U 或 E.

在文氏图一般使用方形表示全集。

eg：在立体几何中，全集是由空间的全体点组成的；

       在我国的人口普查中，全集是由我国所有人组成的。

全集是相对唯一的

3.相等关系

两个集合 具有相同的元素, 此时称两个集合相等

eg：E = {x|(x − 1)(x − 2)(x − 3) = 0, x ∈ R}, F = {x|x ∈ Z +, x 2 < 12},

可见 E 和 F 具有相同的元素 {1, 2, 3}, 此时称两个集合相等

元素的基本特性

1.集合中的元素是无序的。     {1, 2, 3, 4} 与 {2, 3, 1, 4} 相同。

2.集合中的元素是不同的。     {1, 2, 2, 3, 4, 3, 4, 2} 与 {1, 2, 3, 4} 相同。

外延性定理

两个集合 A 和 B 相等，当且仅当它们的元素完全相同，记为 A = B,

否则 A 和 B不相等，记A ≠ B

 证明集合相等

设 A, B 为任意两个集合，则 A = B ⇔ A ⊆ B 并且 B ⊆ A

4.包含关系

设 A,B 是任意两个集合，

如果 B 的每个元素都是 A 中的元素，则称 B 是 A 的子集，也称做B 被 A 包含或A 包含 B，记作B ⊆ A，否则记作B ⊈ A.

如果 B ⊆ A 并且 A ̸= B，则称 B 是 A 的真子集，也称做B 被 A 真包含或A 真包含 B，记 作B ⊂ A，否则记作B ̸⊂ A.

重要定理

”⊆” 关系的数学语言描述为：B ⊆ A ⇔ 对 ∀x, 如果 x ∈ B，则x∈A

由子集定义可有

1. ∅ ⊆ A

2 .A ⊆ A

5.幂集

设 A 为任意集合，把 A 的所有不同子集构成的集合叫做 A 的幂集(power set), 记作 P(A)，

即， P(A) = {x|x ⊆ A}

eg：设 A = {a, b, c}，B = { a, {b, c} } ，求他们的幂集 P(A) 和 P(B)。

解：P(A) = { ∅, {a}, {b}, {c}, {a, b}, {b, c}, {a, c}, {a, b, c} }

P(B) = { ∅, {a}, { {b, c} } , { a, {b, c} }}

x ∈ P(A) ⇔ x ⊆ A     即 幂集的元素⇔ 集合的子集

集合的运算

1.交运算

A ∪ B

2.并运算

A ∩ B

3.差运算

A − B

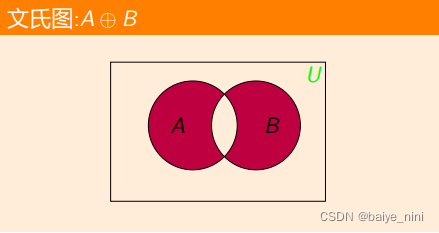
4.对称差集      即交集的补集

A ⊕ B = {x|(x ∈ A 并且 x ∉ B)或者(x ∉ A 并且 x ∈ B)}

5.补集

A = {x|x ∈/ A}

集合的运算定律

证明以上定律，可以用文氏图的方式，也可以用数学证明的方式。 

进行数学证明，要用到证明集合相等的知识      传送门：3.相等关系

例： 

可数集合与不可数集合

1.等势

设 A, B 为两个集合，若在 A, B 之间存在一种一一对应的关系：

                              Ψ : A → B

则称 A 与 B 是等势的 (equipotential)，记作： A ∼ B

由等势定义可以看出，如果 A = B，那么 A ∼ B，反之不成立

2.可数集合

凡与自然数集合 N 等势的集合，称为可数集合(countable set)，

该集合的基数记为ℵ0(读作阿列夫零) 

eg：下列集合都是可数集合.

(1) O+ = {x|x ∈ N, x是正奇数};

(2) P = {x|x ∈ N, x是素数};

(3)有理数集合Q

可数集合的基数都是一样的，基数为ℵ0

 3.不可数集合

开区间 (0, 1)称为不可数集合，

凡与开区间 (0, 1) 等势的集合，称为不可数集合，

该类集合的基数记为ℵ(读作阿列夫)

eg：闭区间【0，1】，实数集合R都是不可数集合。