1.1. 综述
随机变量
样本空间到实数轴的函数,
分布函数,概率密度函数
,k阶矩
随机过程
多个随机变量的关系
(1). 线性相关
时域
频域
Gaussian过程
(2). 马尔可夫性
1). 离散时间
2). 连续时间
3). Poisson过程
(3). 鞅(Martingale)
金融领域
1.2. 线性相关
相关性:二元的

矩形,Y的分布不随X改变而改变,独立

圆形,范围改变期望不变,不独立但不是线性相关
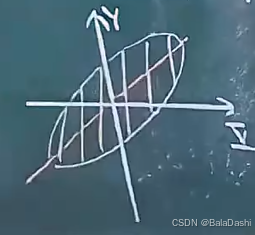
纺锤形,期望改变且范围改变,线性相关,Y的取值范围随X增大而增大,若纺锤宽度为0,则为线性关系。
符号说明
Y~kX,Y的期望与X成线性的关系,引入距离度量,均方距离,将Y与kX带入:
其中的交叉项就是X和Y的相关
相关有两个特点:
(1). 相关是一种内积,具有:正定性、对称性、双线性;
(2). 视为几何中的角度,从而理解正交。
由此,可得相关的性质。
1.3 相关的性质
1.3.1 与独立的关系
独立与不相关(正交,,若X,Y均值为0,则
)的关系为
独立一定不相关,不相关不一定独立
1.3.2 柯西不等式
1.3.3 自相关矩阵
,
即为自相关矩阵。
自相关矩阵对称且正定。
对称性证明
正定性的证明
而且为一个数(
中所有元素的平方和),故
,
正定。
1.4 随机函数
若对定义域内的一个自变量,均有一个随机变量
与之对应(一般的函数对应的是一个确定的值),则表示该随机过程的函数
(也可写作
)被称为随机函数。大多数情况下,随机过程和随机函数等价。随机函数的一组值被称为样本轨道,例如股票曲线,一天确定的值就是一组样本轨道,而当天的曲线有无数种可能。
对一个随机函数,在不同时刻取值的乘积的期望,被称为(自)相关函数。
相关函数即是连续随机变量的相关矩阵,同样具有对称性和正定性,且满足柯西不等式。即
证明略。
1.5 随机过程的平稳性质
宽平稳(w.w.s.)性质:
① ,其中,为
确定函数或常数
②,也可以写作
由以上两个特性可以判断随机过程是否满足宽平稳,并得出以下推论
③
④如果宽平稳,且
,则
⑤如果在
连续,则
处处连续。
1.10 补充知识:
1.10.1 重要分布:
离散:伯努利、二项、Poisson分布
连续:均匀、指数、Gaussian
1.10.2 柯西不等式证明(内积)
内积形式的柯西不等式为
证明:构造辅助函数
有非负性,且其展开为
对是开口向上的函数,其
判别式为
由于开口向上且非负,
无解或只有一个解,故
即
两边开方
得证!
1.10.3 相关函数性质④证明
性质④:如果宽平稳,且
,则
证明: 若要证明,考虑先证明
由,可知
,左边还等于
即有
又因为
期望具有线性性质,有
由于乘积的绝对值小于等于绝对值的乘积,
























 5793
5793

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








